针对在线学习系统中时序认知诊断的概率框架
A Probabilistic Framework for Temporal Cognitive Diagnosis in Online Learning Systems
-
摘要:研究背景
认知诊断(Cognitive Diagnosis)在医疗、游戏、教育等现实场景中是一项基础且重要的任务。特别的,在智能教育系统中,认知诊断常被用于识别学生在学习过程中的状态。它旨在通过学生历史答题记录,分析他们在微观层面的知识状态和技能水平,如在各个知识点上的掌握程度。依据诊断结果,学生可以发现自己薄弱的知识点,而教学者能为不同学生提供针对性的指导意见,如推荐相关的试题、教学资源等,实现因材施教。因此,认知诊断方法是实现个性化、智能化教育的重要课题,而如何准确地实施认知诊断是一个关键的问题。
目的本文的目的是建立适用于在线学习场景的认知诊断框架,该场景下学生作答过程中的时序性与随机性是两个重要因素。具体而言,在线学习场景中学生的状态会随时间演变,因此需要从时序(temporality)的角度考虑学生的作答记录。同时,学生状态演变具有随机性(randomness),并不能以确定性的方式如曲线、规则或神经网络描述其变化过程。 当前先进的模型如TIRT,T-SKIRT仅在模型推断时引入上述两个因素,采用不一致的训练-推断过程。本文希望提出一致(unified)的诊断框架,同时在训练参数与推断状态方法中建模上述因素。
方法论文首先从学生状态演变过程的特点出发,分析不同时刻认知状态之间的关系,提出“学生能力演化服从维纳过程(Wiener process)”假设,同时建模了状态变化的时序性与随机性。随后,论文针对上述复杂概率图模型的训练过程,依据学生实际作答过程,提出“k时刻的作答记录对诊断k时刻认知状态的作用最大”的假设,从另一角度加强对时序性的建模,并解决了期望最大化(Expectation Maximization, EM)算法中M步难以估计的问题,基于此实现了统一训练过程与推断过程的目标。最后,我们证明了提出的框架(UTIRT)具有更好的泛化性,传统方法如IRT,MIRT和TIRT均是其特例。
结果在两个在线教育数据集上,我们从三个角度设计了多组实验,对比10个基线模型,我们的框架取得了更高的准确率和更低的错误率。从认知状态诊断角度,本方法准确率(ACC)提升了0.8%—10.1%,同时分别在ASSIST, Junyi数据集上获得了最优的AUC(提升0.3%—11.4%)和RMSE(降低0.2%—5.2%)。通过对实验结果的进一步分析,我们发现本方法在序列性更强的数据集上的提升更为明显,同时,考虑知识点关系、合理选择超参数也能改善认知诊断结果。 从作答预测角度,本方法获得了最优的ACC(提升0.5%—9.9%)和AUC(提升0.1%—12.2%)。上述结果从多个角度验证了时序性、随机性因素的有效性。从时序性使用分析角度,我们通过假设检验验证了不统一的训练、推断过程会带来潜在假设上的矛盾(两个数据集上的p值分别为4.61×10–6,6.08×10–3)。同时,基于不同“保留长度”的记录序列实施诊断时,UTIRT的预测准确度始终明显优于TIRT,更好地验证了统一训练、推断过程的重要性。
结论针对在线学习场景,本文提出了一种同时建模学生能力变化过程中时序性和随机性的UTIRT框架。实验结果表明,时序性与随机性对认知诊断结果具有显著影响。我们观察到,引入这两种因素均能更好地从答题序列中捕捉学生状态变化信息,从而准确地诊断学生的认知状态。其他因素如框架一致性、知识点关系、超参数选择也对诊断效果有重要的影响。此外,我们讨论了其他可能的改进,如利用学生对同一题目的多次尝试、提示的使用和作答时间等数据更准确地建模学生认知状态变化过程。
Abstract:Cognitive diagnosis is an important issue of intelligent education systems, which aims to estimate students’ proficiency on specific knowledge concepts. Most existing studies rely on the assumption of static student states and ignore the dynamics of proficiency in the learning process, which makes them unsuitable for online learning scenarios. In this paper, we propose a unified temporal item response theory (UTIRT) framework, incorporating temporality and randomness of proficiency evolving to get both accurate and interpretable diagnosis results. Specifically, we hypothesize that students’ proficiency varies as a Wiener process and describe a probabilistic graphical model in UTIRT to consider temporality and randomness factors. Furthermore, based on the relationship between student states and exercising answers, we hypothesize that the answering result at time k contributes most to inferring a student's proficiency at time k, which also reflects the temporality aspect and enables us to get analytical maximization (M-step) in the expectation maximization (EM) algorithm when estimating model parameters. Our UTIRT is a framework containing unified training and inferencing methods, and is general to cover several typical traditional models such as Item Response Theory (IRT), multidimensional IRT (MIRT), and temporal IRT (TIRT). Extensive experimental results on real-world datasets show the effectiveness of UTIRT and prove its superiority in leveraging temporality theoretically and practically over TIRT.
-
1. Introduction
Cognitive diagnosis (CD) is a necessary and fundamental task in many real-world scenarios such as medical diagnosis[1, 2], games[3], and education[4]. Specifically, in intelligent education systems, it aims to discover students' states in the learning process, such as diagnosing their proficiency on specific knowledge concepts, based on their historical records of answering exercises[4]. Fig.1 shows a toy example of CD. Student s1 has practiced a set of exercises (e.g., e1, e2, e3, e4) and gets responses (e.g., right or wrong). Our goal is to diagnose his/her mastery (e.g., 0.7, 0.2) of the corresponding knowledge concepts (e.g., “greatest_common_divisor”). Such diagnosis results are useful in reality as they provide actionable information about students' weakness and help develop customized remediation to improve students' performance, such as exercise recommendations and targeted training[5].
![]() Figure 1. Example of students' exercising records. (a) Exercises e1 to e4 with the same knowledge concept “greatest_common_divisor”. (b) Probability density function of s1’s and s2’s proficiency distribution: the y axis is the proficiency value (ranging from 0 to 1) and the x axis is the corresponding probability density. (c) Diagnosis results: 0.7 and 0.2 for s1 and s2 respectively.
Figure 1. Example of students' exercising records. (a) Exercises e1 to e4 with the same knowledge concept “greatest_common_divisor”. (b) Probability density function of s1’s and s2’s proficiency distribution: the y axis is the proficiency value (ranging from 0 to 1) and the x axis is the corresponding probability density. (c) Diagnosis results: 0.7 and 0.2 for s1 and s2 respectively.In the literature, a variety of promising researches on CD have been developed, such as Determinisic Input, Noisy-And gate model (DINA)[6], Item Response Theory (IRT)[7], Multidimensional IRT (MIRT)[8], Temporal IRT (TIRT)[9], Rule Space Model (RSM)[10], Attribute Hierarchy Methods (AHM)[11], Probabilistic Matrix Factorization (PMF)[12], and Neural Cognitive Diagnosis (NeuralCD)[4]. Among them, IRTs (e.g., IRT, MIRT) have been attached with great importance and widely used in industry. Nevertheless, most of existing methods focus on static scenarios (e.g., standard test) with a short duration of finishing exercises, thus assuming that each student's proficiency remains static and does not change over time. However, as considered in online learning scenarios, students take a long time to do exercises and get (e.g., from online systems) correct answers, instructions and other learning materials to acquire knowledge. In fact, educational psychologists have long converged[13] that the learning process of students evolves over time, as students acquire and forget knowledge they have learned. Theories like the Learning Curve theory[14] and the Forgetting Curve theory[15, 16] were proposed to capture the change of students' proficiency. From the perspective of data, it means exercising records contain temporal information, and the latest records contribute more to diagnosing a student's present proficiency.
Taking student s1 shown in Fig.1 as an example, s1 has finished exercises e1 to e4 with the same knowledge concept “greatest_common_divisor” in sequence and responds r1, r2, r3, r4, and we want to evaluate whether he/she masters “greatest_common_divisor” after finishing these four exercises. From the record sequence, we tend to believe that s1 has mastered this knowledge concept, since the latest records r3 and r4 are correct, even though he/she made mistakes at the beginning. Nevertheless, the traditional CD models treat every history as the same. It will lead to a wrong conclusion that s1 has not mastered “greatest_common_divisor”, since only half of the exercises are answered correctly. To solve this problem, it is necessary to introduce temporality into CD models, i.e., treating students' records as a sequence and modeling the change of students' proficiency.
In addition, the learning process is not deterministic because the degree of students' mastery after finishing an exercise is uncertain. Different students acquire and forget knowledge to different degrees when doing the same exercise. As shown in Fig.1, students s1, s2 have the same answers on the first three exercises but respond differently on e4, indicating that they may have different mastery degrees on knowledge concept “greatest_common_divisor” even after finishing the same exercises and getting the same results. Moreover, even if a student practices the same exercise based on the same knowledge state, he/she may have different answers and update proficiency differently. Therefore, when modeling temporality, we also need to incorporate randomness, i.e., students' proficiency is a random variable and the change of proficiency is a stochastic process.
Combining these two factors, a student's proficiency at each moment is represented as a distribution, which is changing during the exercising process, as shown in Fig.1. When s1 answers wrong on e1, e2, the peak of the probability density function of proficiency distribution skews towards 0, and the variance gets smaller, meaning that we are more confident to state that s1 fails on mastering the knowledge concept. On the contrary, as s1 answers right on e3, e4, the peak of the probability density function of proficiency distribution moves towards 1. By incorporating randomness, s1, s2 have the same distribution in the first three exercises (because they have the same records), instead of the same proficiency value, which explains why they could respond differently on e4.
There are few previous researches considering these two factors. To the best of our knowledge, TIRT[9] is a state-of-the-art method incorporating temporality into the IRT framework by exploiting a Wiener process[17] to describe students' proficiency evolving. However, in TIRT, temporality is considered only when inferring students' states, which is inconsistent with its training (model parameter estimation) assumption. Comparatively, models like IRT and NeuralCD make more sense since they use the same settings for training and inferencing. Intuitively, these models with unified training/inferencing methods are preferable.
In this paper, we propose a unified temporal item response theory (UTIRT) framework which is a probabilistic graphical model and incorporates temporality and randomness of students' proficiency. Although the capability of probabilistic graphical models to represent the joint probability distribution of multiple random variables (in our case, a student's proficiency and performance scores at different time points) has been proved and many probabilistic graphical models have been proposed in various domains[18–20], it is still nontrivial to adapt to CD due to the following challenges. First, parameter estimation in probabilistic graphical models is relatively difficult, especially in the CD scenario, where a student's knowledge state is an implicit variable. The classic algorithm for the incomplete observation problem is the expectation maximization (EM) algorithm. However, the setting of dynamic students' proficiency increases computational complexity, brings difficulty in deriving the maximization (M-step) in the EM algorithm, and even makes parameter estimation intractable. Second, to simplify computation, it is common to use some approximations (hypotheses) like variational inference. Nevertheless, such hypotheses should be explainable and reasonable under the CD task and reflect the students' real states of doing exercises, which is increasingly important in practical applications. Therefore, it brings the challenge of utilizing approximations to reduce computational complexity while ensuring interpretability.
To address these challenges, we propose two hypotheses in the UTIRT framework while preserving explainability. We first hypothesize that the change of students' proficiency over time can be modeled as a Wiener process. It lays a basic foundation for our probabilistic graphical model and involves the temporality and randomness aspects. For interpretability, the intuitive ideas behind are explained as follows. Firstly, after finishing an exercise, a student updates the knowledge state based on the current state, by realizing the weakness of present cognition, acquiring new knowledge, and forgetting it. We implement this idea by setting the mean of proficiency distribution at time t+1 as the proficiency at time t, and the Gaussian distribution in the Wiener process is an easy form to achieve such guarantee. Secondly, there are relationships between different knowledge concepts, and we can model such effects by a covariance matrix in the Gaussian distribution. After that, we propose the second hypothesis: the response at time k contributes most to inferring a student's proficiency at time k, since he/she answered the question at time k directly according to corresponding proficiency at time k. Combined with this hypothesis, the maximization (M-step) in the EM algorithm becomes analytic and further makes parameter estimation of our model tractable. Based on these two hypotheses, we formulate the probabilistic graphical model in UTIRT and deduce corresponding training (i.e., the EM algorithm) and inferencing (maximum a posteriori estimation) methods. Particularly, our UTIRT is a general framework. We prove that it covers many traditional models such as IRT, MIRT, and TIRT.
The proposed method is evaluated on two datasets collected by online tutoring systems and platforms by using different evaluation metrics. The results show that our method obtains the equivalent results of the state-of-the-art models, on both knowledge proficiency estimation and next score prediction tasks. In addition, we conduct hypothesis testing and compare prediction results of different “keep length” to demonstrate that our method better utilizes the temporality of students' proficiency than TIRT. The main contributions of this work can be summarized as follows.
● A UTIRT framework is proposed for the CD task. Compared with existing methods, the proposed framework considers temporality and randomness of students' proficiency, and provides unified training and inferencing methods.
● Two hypotheses are adopted to simplify modeling and calculation, and we explain the ideas behind these two hypotheses, which makes our framework more interpretable.
● The proposed framework is evaluated on two real-world datasets, and the results show that it obtains similar results in general CD tasks compared with several baseline methods, and performs better in tasks when the sequentiality of students' records is important.
2. Related Work
2.1 Cognitive Diagnosis
In recent years, CD, as the core of education and measurement theory, has received extensive attention in pedagogy, psychology, and other fields[21]. Many CD models have been proposed, which can be divided into two aspects: unidimensional and multidimensional.
IRT[7] is a typical unidimensional model that models each student as a proficiency variable and predicts the probability a student will answer an exercise correctly based on an item response function, which can be chosen as the logistic function or the cumulative distribution function of the Gaussian distribution[22]. The Latent Factor Model (LFM)[23] is a special version of IRT that only considers the difference between proficiency and exercise difficulty. TIRT[9] extends IRT by modeling a student's proficiency θ as a Wiener process:
P(θt+τ|θt)∝exp[−(θt+τ−θt)2/2γ2τ], where θt and θt+τ are the student's proficiency at time t and t+τ respectively, and γ is a hyper-parameter controlling the “smoothness” with which the knowledge state varies over time.
As for multidimensional approaches, DINA[6] models a student's proficiency as multiple binary variables, each of which indicates whether or not he/she has mastered the corresponding knowledge concept. Only when a student masters all knowledge concepts required for the exercise, can he/she answer it right. MIRT[8] extends students' traits and exercises' features in IRT to be multidimensional. In MIRT, students' proficiency is denoted as a multidimensional variable {\boldsymbol{\theta}} , and exercise discrimination and difficulty parameters are denoted as {\boldsymbol{\alpha}} and \; {\boldsymbol{\beta}} , respectively. Temporal structured-knowledge IRT (T-SKIRT)[24] adopts the same stochastic process as TIRT. However, it considers the prerequisite relationships between different knowledge concepts and employs a specific multivariate Gaussian prior of proficiency when inferring a student's state. NeuralCD[4] is a general neural CD framework, which incorporates neural networks to learn the complex interactions between students and exercises, and gets interpretable diagnosis results. In order to ensure interpretability, it proposes a monotonicity assumption achieved by restricting parameters in neural networks to be positive.
Most of these traditional models do not consider the sequentiality of students' records and implicitly assume that a student's proficiency does not change over time. It is improper in some cases and limits their applications. Though TIRT and T-SKIRT model students' proficiency evolving as a Wiener process, there are several improvements in our UTIRT. First, UTIRT is a unified framework modeling temporality in both training and inferencing methods, while TIRT and T-SKIRT only utilize temporality in the inferencing phase, which is unreasonable and results in conflicts between these two phases. Second, when describing students' proficiency evolving by the Wiener process, UTIRT incorporates the influence among different knowledge concepts, while TIRT and T-SKIRT ignore such effects. Indeed, T-SKIRT only utilizes the prerequisite relationships as a prior over students' knowledge states, which works as a static regularization in the inferencing phase. From this perspective, UTIRT also adopts unified use of the relationships between knowledge concepts compared with T-SKIRT. Last but not least, our UTIRT learns the parameters in the Wiener process, instead of setting them as hyper-parameters adopted in TIRT and T-SKIRT, which brings better generalization ability.
2.2 Dynamic Learning Process Modeling
Several theories and models have been proposed to describe the dynamics of students' proficiency during the learning process. The Learning Curve Theory[14] and the Forgetting Curve Theory[15, 16] are two typical theories. Specifically, the Learning Curve Theory provides a mathematical description of students acquiring knowledge and improving performances when constantly doing exercises, and the Forgetting Curve Theory points out a decreasing memory of students on knowledge they have learned. Based on these two theories, varieties of studies have been developed for diagnosing students' states from a dynamic perspective[25]. For example, some IRT-based models, such as Learning Factors Analysis (LFA)[26] and Performance Factors Analysis (PFA)[27], assume that students share the same parameters of learning rate during exercising, while PFA further tracks response sequence by using previous k attempts. Dynamic Item Response (DIR)[13], a variant of IRT, focuses on time series dichotomous response data and incorporates time-dependent exercise parameters and daily random effects. In addition, the Elo rating schema[28] updates students' ability and exercises' parameters based on the difference between the true answer and the predicted probability when new data are observed[29–32]. Longitudinal cognitive diagnosis[33–37] evaluates students' knowledge over time by incorporating the transition probability of latent class or high-order latent ability.
Another representative work to model the dynamic process of students' mastering skills is knowledge tracing (KT)[38–51]. One of the classical models is Bayesian Knowledge Tracing (BKT)[38]. BKT is a knowledge-specific model which represents each student's knowledge state as a set of binary variables, where each variable represents whether he/she has mastered a specific skill. It utilizes a hidden Markov model (HMM) to update the knowledge state of each student. Current variants of BKT mostly focus on individual factors, such as individual student prior[45], learn rate[46], individual exercise guess, slip[41, 52], and resource learn rate[53]. As deep learning methods outperform many conventional models in various domains, Piech et al.[47] used the recurrent neural network (RNN) and the long short-term memory (LSTM) network to model the evolving proficiency on concepts and proposed Deep Knowledge Tracing (DKT), representing proficiency as a high-dimensional and continuous vector. Another popular deep learning model is Deep Key-Value Memory Network (DKVMN)[48], which leverages one static key memory matrix to store knowledge concepts and one dynamic value memory matrix to store and update the mastery levels. DKVMN is able to learn the correlations between exercises and underlying concepts, which improves the interpretability of the prediction results.
Despite the importance of these efforts, there are still some limitations in practice. First, these IRT-based models only estimate a specific variable for each student; thus they are unable to model the interactions between different knowledge concepts. Second, some deep learning based models operate like a black box, where the evolution of a student's proficiency and the prediction process given his/her knowledge state are usually represented as neural networks. Thus, the outputs of prediction and state representation are hard to explain. Last but not least, most existing models, including BKTs and DKTs, neglect the randomness of students' proficiency evolving. That is to say, these models assume implicitly if a student's proficiency {\boldsymbol{\theta}}^t and historical scores are given, his/her knowledge state at time t+1 is certain and can be calculated accurately (e.g., by a curve, update rules or neural networks), which is unreasonable in reality. Although longitudinal CD models consider the randomness of attribute transition, existing work[32-36] focuses on binary attributes and ignores the influence among different knowledge concepts. In contrast, our method improves traditional approaches by relying on a hypothesis to describe students' high-dimensional knowledge states evolving in a random and overall way, while guaranteeing explanatory power.
3. Proposed Method: UTIRT
In this section, we first give the necessary definition of the CD task. Then we introduce the details of our UTIRT framework. After that, we illustrate the training and inferencing methods of UTIRT. Finally, we demonstrate the generality of UTIRT by showing its relationship with other work.
3.1 Problem Definition
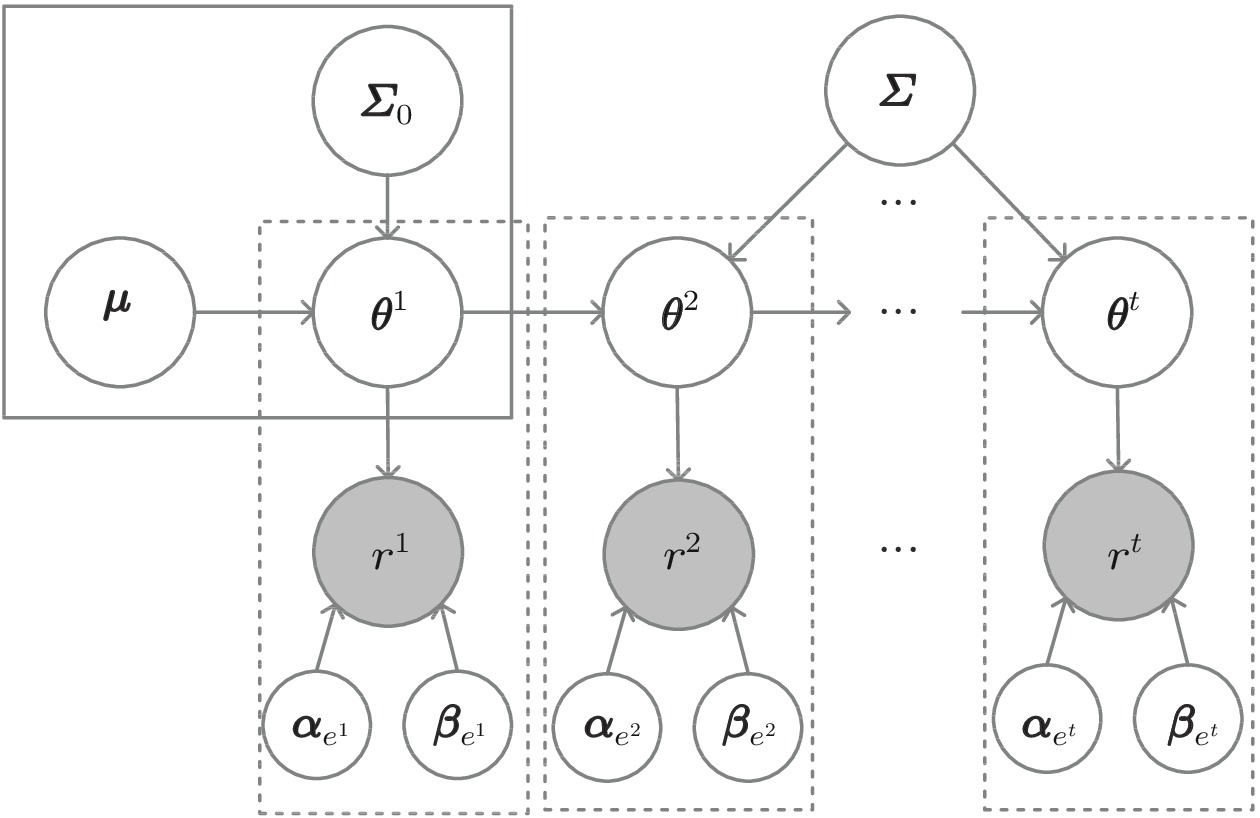
Assuming that there are N students, M exercises and K knowledge concepts in an education system, we record the exercising process of student i as s_i = \{s^1_i,s^2_i,\ldots,s^{T_i}_i\} , where T_i is the number of his/her historical records. At each time t , s^t_i = (e^t_i, r^t_i) , where e^t_i represents the exercise solved by student i at time t , and r^t_i denotes the corresponding result. Generally, r^t_i is an observed binary variable equal to 1 if student i answers exercise e^t_i correctly, and 0 otherwise.
Given a student i 's sequence of answered exercises and results s_i , our goal is to diagnose his/her proficiency at time T+1 , which is represented as a K -dimensional vector {\boldsymbol{\theta}}^{T+1}_i \in {\mathbb{R}}^K . ({\boldsymbol{\theta}}^{T+1}_i)_j reflects the proficiency of student i on knowledge concept j (e.g., “Function in Math”). Therefore, {\boldsymbol{\theta}}^{T+1}_i represents i 's proficiency on all K knowledge concepts after finishing T exercises.
3.2 Model Framework
First, we specify how to model the temporality and randomness of students' proficiency {\boldsymbol{\theta}}^{t} . Intuitively, after finishing an exercise, a student acquires new knowledge, reinforces or forgets mastered knowledge, and his/her proficiency is updated based on present proficiency. Therefore, his/her proficiency {\boldsymbol{\theta}}^{t+1} at time t+1 distributes around {\boldsymbol{\theta}}^{t} . We model this idea with randomness by setting the expectation of {\boldsymbol{\theta}}^{t+1} equal to {\boldsymbol{\theta}}^{t} , i.e., E[{\boldsymbol{\theta}}^{t+1}|{\boldsymbol{\theta}}^{t}] = {\boldsymbol{\theta}}^{t} , which we call mean guarantee. In general, we expand this idea with temporality to model the relationship between {\boldsymbol{\theta}}^{t} and {\boldsymbol{\theta}}^{t+k} , i.e., E[{\boldsymbol{\theta}}^{t+k}|{\boldsymbol{\theta}}^{t}] = {\boldsymbol{\theta}}^{t} . An important factor that needs to be considered is the relationship between different knowledge concepts. For example, acquiring the concept “add in Math” may result in a better understanding of “multiply in Math” because students must learn to add before they can multiply. Then, the variation of proficiency on “multiply in Math” will further influence other concepts. Therefore, there are complex correlations between different knowledge concepts. Based on these ideas, we propose the first hypothesis.
Assumption 1. The change of students’ proficiency over time can be modeled as a Wiener process.
A Wiener process[17] is a random process, stating that the increment of a variable between any two moments s and t is normally distributed with mean zero and variance |s-t| . It models the temporality and randomness simultaneously and achieves our mean guarantee by restricting the mean of the Gaussian distribution to zero. Moreover, it can be extended to be multidimensional and incorporate the relationships between different knowledge concepts by setting the covariance matrix of the Gaussian distribution. Such relationships are stable and do not depend on time, and thus we introduce a time-independent parameter matrix {\boldsymbol{\varSigma}} in {\boldsymbol{\theta}}^{t+k} 's distribution. Under these settings, the distribution of proficiency {\boldsymbol{\theta}}^{t+k} conditional on {\boldsymbol{\theta}}^t is given by
P({\boldsymbol{\theta}}^{t+k}|{\boldsymbol{\theta}}^t) = {\cal{N}}({\boldsymbol{\theta}}^{t+k}|{\boldsymbol{\theta}}^t, k\cdot {\boldsymbol{\varSigma}}), (1) where {\cal{N}}(\cdot|{\boldsymbol{\mu}},{\boldsymbol{\varSigma}}) is the probability density function of the multivariate Gaussian distribution with mean {\boldsymbol{\mu}} and covariance matrix {\boldsymbol{\varSigma}} . In (1), covariance matrix k\cdot {\boldsymbol{\varSigma}} is the multiplication of matrix {\boldsymbol{\varSigma}} and value k , which indicates that as the time interval k increases, the deviation from proficiency at time t+k to t becomes greater. Moreover, we also assume the initial proficiency (i.e., no exercises are answered) {\boldsymbol{\theta}}^{1} follows {\cal{N}}({\boldsymbol{\theta}}^{1}|{\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0) . Mean vector {\boldsymbol{\mu}} \in {\mathbb{R}}^K and covariance matrices {\boldsymbol{\varSigma}}, {\boldsymbol{\varSigma}}_0 \in {\mathbb{R}}^{K\times K} are model parameters, which need to be optimized by maximum likelihood estimation. For a student, the joint probability of his/her responses and proficiency is
\begin{split}&P(r^1,r^2,\ldots,r^t,{\boldsymbol{\theta}}^{1:t}) \\ =\ &P({\boldsymbol{\theta}}^1)\prod\limits_{k = 2}^{t}P({\boldsymbol{\theta}}^k|{\boldsymbol{\theta}}^{k-1})\prod\limits_{k = 1}^{t}P(r^k|{\boldsymbol{\theta}}^k) \\ = \ & {\cal{N}}({\boldsymbol{\theta}}^{1}|{\boldsymbol{\mu}}, {\boldsymbol{\varSigma}}_{0}) \prod\limits_{k = 2}^{t} {\cal{N}}({\boldsymbol{\theta}}^{k}|{\boldsymbol{\theta}}^{k-1},{\boldsymbol{\varSigma}}) \times \\ &\prod\limits_{k = 1}^{t} p_{k}^{r^{k}}\left(1-p_{k}\right)^{1-r^{k}}, \end{split} (2) where r^k is the answer of exercise e^k at time k , which equals 1 if the student answers correctly, and 0 otherwise, {\boldsymbol{\theta}}^{k} is the proficiency vector of the student at time k , which is unobservable and unknown, p_k is the probability that a student with proficiency {\boldsymbol{\theta}}^k answers exercise e^k correctly and the general form is p_k = f({\boldsymbol{\theta}}^k; e^k) . Please note that there are several designs for the expression of f , and we implement it as MIRT[8] because MIRT models the relationship between students' ability and answers in a concise way. Formally in MIRT, the probability of answering correctly is
f({\boldsymbol{\theta}}; q) = {\varPhi}[{\boldsymbol{\alpha}}_q^{\mathrm{T}}\cdot ({\boldsymbol{\theta}}-{\boldsymbol{\beta}}_q)], (3) where {\varPhi} is the item response function which roots in the psychological measurement theory, and {\boldsymbol{\alpha}}_q,\ {\boldsymbol{\beta}}_q are the discrimination vector and the difficulty vector of exercise q respectively. We choose {\varPhi} as the cumulative distribution function of the Gaussian distribution, which is known as the 2PO model[22]. The reason is that the probability density function of the Gaussian distribution has some useful integral properties which help to derive an analytic solution in subsequent computations as shown in the training and inferencing methods.
In summary, we have proposed the framework of UTIRT by suggesting a Wiener hypothesis to model the evolution of students' proficiency and using MIRT to predict answers. We summarize the corresponding probabilistic graphical model of UTIRT in Fig.2, where the shaded r^t indicates the observed answer result, and the other unshaded variables indicate the latent proficiency and parameters.
3.3 Model Training
Under the UTIRT framework above, our goal is to learn the parameters {\varTheta} = \{{\boldsymbol{\mu}}, {\boldsymbol{\varSigma}}_0, {\boldsymbol{\varSigma}}, {\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q|q = 1, 2,\ldots, M\} . Since a student's proficiency is an unobserved variable, we use the EM algorithm to maximize the likelihood of students' answer records, which is suitable for the incomplete observation problem. The EM algorithm is an iterative algorithm containing expectation (E-step) and maximization (M-step). In each iteration i , it updates parameters {\varTheta} (i.e., M-step) by:
\begin{split} {\varTheta}^{i+1} =& \mathop {{\rm{argmax}}}\limits_{\varTheta} \int P({\boldsymbol{\theta}}|R, {\varTheta}^{i}) \ln P(R, {\boldsymbol{\theta}}| {\varTheta}) \mathrm{d} {\boldsymbol{\theta}}\\= &\mathop {{\rm{argmax}}}\limits_{\varTheta} \sum\limits_{R_j} \int P({\boldsymbol{\theta}}^{1}_j, {\boldsymbol{\theta}}^{2}_j, \ldots, {\boldsymbol{\theta}}^{t_{j}}_j | R_{j}, {\varTheta}^{i}) \times \\&\ln P(R_{j}, {\boldsymbol{\theta}}^{1}_j, {\boldsymbol{\theta}}^{2}_j, \ldots, {\boldsymbol{\theta}}^{t_j}_j | {\varTheta}) \mathrm{d} {\boldsymbol{\theta}}^{1}_j\mathrm{d} {\boldsymbol{\theta}}^{2}_j \ldots \mathrm{d}{\boldsymbol{\theta}}^{t_{j}}_j, \end{split} (4) where {\varTheta}^i are parameters obtained after iteration i-1 , R_j = (r^1_j,r^2_j,\ldots,r^{t_j}_j) is the j -th record (the whole answer sequence of a student) in training data D with length t_j , and {\boldsymbol{\theta}}^1_j, {\boldsymbol{\theta}}^2_j,\ldots,{\boldsymbol{\theta}}^{t_j}_j are corresponding students' proficiency during exercising, which are unobservable. Combined with (2), (4) is equivalent to the following:
\begin{split} {\varTheta}^{i+1} = &\mathop {{\rm{argmax}}}\limits_{\varTheta}\displaystyle\sum\limits_{R_j}\Bigg(\int P({\boldsymbol{\theta}}^{1}_j | R_{j}, {\varTheta}^{i})\ln P({\boldsymbol{\theta}}^{1}_j |{\varTheta} ) \mathrm{d} {\boldsymbol{\theta}}^{1}_j+\\& \displaystyle\sum\limits_{k = 2}^{t_{j}} \int P({\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\theta}}^{k}_j | R_j, {\varTheta}^{i})\times \\& \ln P({\boldsymbol{\theta}}^{k}_j | {\boldsymbol{\theta}}^{k-1}_j, {\varTheta}) \mathrm{d} {\boldsymbol{\theta}}^{k-1}_j\ \mathrm{d}{\boldsymbol{\theta}}^{k}_j+ \\& \displaystyle\sum\limits_{k = 1}^{t_{j}} \int P({\boldsymbol{\theta}}^{k}_j | R_j, {\varTheta}^{i}) \ln P(r_{j}^{k} | {\boldsymbol{\theta}}^{k}_j, {\varTheta}) \mathrm{d}{\boldsymbol{\theta}}^{k}_j\Bigg). \\[-1pt] \end{split} (5) In (5), \ P({\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\theta}}^{k}_j | R_j, {\varTheta}^{i}) is the posterior probability of students' proficiency at time k-1 and k given the whole answer sequence R_j , and P({\boldsymbol{\theta}}^{k}_j | R_j, {\varTheta}^{i}) is the posterior probability at time k . To attain these terms by the Bayesian law, we have to calculate the prior distribution of R_j , i.e., P(R_j| {\varTheta}^{i}) . However, P(R_j| {\varTheta}^{i}) = \displaystyle\int P(R_{j}, {\boldsymbol{\theta}}^{1}_j, {\boldsymbol{\theta}}^{2}_j, \ldots, {\boldsymbol{\theta}}^{t_j}_j | {\varTheta}^{i}) \mathrm{d} {\boldsymbol{\theta}}^{1}_j \mathrm{d} {\boldsymbol{\theta}}^{2}_j \ldots \mathrm{d} {\boldsymbol{\theta}}^{t_{j}}_j contains the integral of multidimensional variables {\boldsymbol{\theta}}^{1}_j, {\boldsymbol{\theta}}^{2}_j, \ldots, {\boldsymbol{\theta}}^{t_{j}}_j , and thus does not have accurate expression. As a result, there is no analytic solution for (5). To solve this problem, we propose the second hypothesis.
Assumption 2. The response at time k contributes most to inferring a student’s proficiency at time k .
Intuitively, student j answers exercise e^k_j exactly based on his/her proficiency at time k , and thus result r^k_j directly reflects proficiency {\boldsymbol{\theta}}^{k}_j . Therefore, the posterior distribution of proficiency {\boldsymbol{\theta}}^{k}_j given the whole sequence (i.e., P({\boldsymbol{\theta}}^{k}_j | R_j, {\varTheta}^{i}) ) is approximately equal to the distribution given only record r^k_j . This idea can also be applied to P({\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\theta}}^{k}_j | R_j, {\varTheta}^{i}) . Mathematically, the approximation is expressed as follows:
\left\{\begin{aligned}&P({\boldsymbol{\theta}}^{k}_j | R_{j}, {\varTheta}^{i}) \approx P({\boldsymbol{\theta}}^{k}_j | r^k_{j}, {\varTheta}^{i}), \\& P({\boldsymbol{\theta}}^{k-1}_j,{\boldsymbol{\theta}}^{k}_j | R_{j}, {\varTheta}^{i})\approx P({\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\theta}}^{k}_j | r_{j}^{k-1}, r_{j}^{k}, {\varTheta}^{i}).\end{aligned}\right. (6) Besides, term P({\boldsymbol{\theta}}^{1}_j |{\varTheta} ) in (5) is the prior distribution of proficiency {\boldsymbol{\theta}}^{1}_j , which is assumed to be a Gaussian distribution with parameters {\boldsymbol{\mu}}\ {\rm and}\ {\boldsymbol{\varSigma}}_0 , and thus it can be simplified to P({\boldsymbol{\theta}}^{1}_j |{\boldsymbol{\mu}}, {\boldsymbol{\varSigma}}_0 ) . Similarly, term P({\boldsymbol{\theta}}^{k}_j | {\boldsymbol{\theta}}^{k-1}_j, {\varTheta}) describes the relationship between {\boldsymbol{\theta}}^{k}_j and {\boldsymbol{\theta}}^{k-1}_j , which is given by (1) and depends only on {\boldsymbol{\varSigma}} . Therefore, it equals P({\boldsymbol{\theta}}^{k}_j | {\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\varSigma}}) . P(r_{j}^{k} | {\boldsymbol{\theta}}^{k}_j, {\varTheta}) evaluates the probability that students with proficiency {\boldsymbol{\theta}}^{i} get result r_{j}^{k} , which is an MIRT form function and only relies on parameters \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q|q = 1,2,\ldots,M\} .
Using these simple mathematical transformations, parameters {\varTheta} are divided into three parts: \{{\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0\} (occurring only in the first term of (5)), {\boldsymbol{\varSigma}} (occurring only in the second term of (5)), and \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q|q = 1,2,\ldots,M\} (occurring only in the third term of (5)). Therefore, optimizing {\varTheta} in (5) is equivalent to optimizing these three parts separately. Combined with (6), the optimization objective in (5) turns to the following equation:
\begin{split} &{\varTheta}^{i+1} \approx \mathop {{\rm{argmax}}}\limits_{\varTheta}\sum\limits_{R_j}\Bigg(\underbrace{\int P({\boldsymbol{\theta}}^{1}_j | r^1_{j}, {\varTheta}^{i})\ln P({\boldsymbol{\theta}}^{1}_j |{\boldsymbol{\mu}}, {\boldsymbol{\varSigma}}_0) \mathrm{d} {\boldsymbol{\theta}}^{1}_j}_{L_1(R_j;{\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0)}+\\& \underbrace{\sum\limits_{k = 2}^{t_{j}} \int P({\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\theta}}^{k}_j | r_{j}^{k-1}, r_{j}^{k}, {\varTheta}^{i}) \ln P({\boldsymbol{\theta}}^{k}_j | {\boldsymbol{\theta}}^{k-1}_j, {\boldsymbol{\varSigma}}) \mathrm{d} {\boldsymbol{\theta}}^{k-1}_j \mathrm{d}{\boldsymbol{\theta}}^{k}_j}_{L_2(R_j;{\boldsymbol{\varSigma}})} + \\& \underbrace{\sum\limits_{k = 1}^{t_{j}} \int P({\boldsymbol{\theta}}^{k}_j | r_{j}^k, {\varTheta}^{i}) \ln P(r_{j}^{k} | {\boldsymbol{\theta}}^{k}_j, \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q\}) \mathrm{d}{\boldsymbol{\theta}}^{k}_j}_{L_3(R_j;{\boldsymbol{\alpha}}_q,\ {\boldsymbol{\beta}}_q)}\Bigg)\\& = \mathop {{\rm{argmax}}}\limits_{{\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0}\sum\limits_{R_j}L_1(R_j; {\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0)+\mathop {{\rm{argmax}}}\limits_{{\boldsymbol{\varSigma}}}\sum\limits_{R_j}L_2(R_j;{\boldsymbol{\varSigma}})+\\&\quad\; \mathop {{\rm{argmax}}}\limits_{\{{\boldsymbol{\alpha}}_q,\ {\boldsymbol{\beta}}_q\}} \sum\limits_{R_j}L_3(R_j;\{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q\})\\&\triangleq \mathop {{\rm{argmax}}}\limits_{{\boldsymbol{\mu}},\ {\boldsymbol{\varSigma}}_0}L_1({\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0) +\mathop {{\rm{argmax}}}\limits_{{\boldsymbol{\varSigma}}}L_2({\boldsymbol{\varSigma}})+\\&\quad\; \mathop {{\rm{argmax}}}\limits_{\{{\boldsymbol{\alpha}}_q,{\boldsymbol{\beta}}_q\}} L_3(\{{\boldsymbol{\alpha}}_q,\ {\boldsymbol{\beta}}_q\}). \\[-1pt] \end{split} (7) Therefore, we can update \{{\boldsymbol{\mu}},{\boldsymbol{\varSigma}}_0\},\ \{{\boldsymbol{\varSigma}}\},\ \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q|q = 1,2,\ldots,M\} by maximizing L_1,\ L_2,\ L_3 , respectively.
To maximize L_1,\ L_2 , we compute their gradients and calculate the extreme points by setting them as zero. We find that both of them have only one extreme point which is the maximum point, and the corresponding solutions are analytic and expressed as follows:
{\boldsymbol{\mu}}^{i+1} = \frac{1}{|D|} \sum\limits_{R_j}\frac{1}{P(r_{j}^{1} | {\varTheta}^{i})} \int P({\boldsymbol{\theta}}^{1}, r_{j}^{1} | {\varTheta}^{i}) {\boldsymbol{\theta}}^{1} \mathrm{d} {\boldsymbol{\theta}}^{1}, (8) \begin{split} {\boldsymbol{\varSigma}}_0^{i+1} =& \dfrac{1}{|D|} \sum\limits_{R_j} \dfrac{1}{P(r_{j}^{1} | {\varTheta}^{i})}\displaystyle\int P({\boldsymbol{\theta}}^{1}, r_{j}^{1} | {\varTheta}^{i})({\boldsymbol{\theta}}^1)^{\mathrm{T}} {\boldsymbol{\theta}}^{1} \mathrm{d} {\boldsymbol{\theta}}^{1}-\\&({\boldsymbol{\mu}}^{i+1})^{\mathrm{T}} {\boldsymbol{\mu}}^{i+1}, \\[-1pt] \end{split} (9) \begin{split} {\boldsymbol{\varSigma}}^{i+1} =& \dfrac{1}{\displaystyle\sum\limits_{R_j}(t_{j}-1)} \displaystyle\sum\limits_{R_j} \displaystyle\sum\limits_{k = 2}^{t_{j}} \dfrac{1}{P(r_{j}^{k-1}, r_{j}^{k} | {\varTheta}^{i})} \int P({\boldsymbol{\theta}}^{k-1}, \\& {\boldsymbol{\theta}}^{k}, r_{j}^{k-1}, r_{j}^{k} |{\varTheta}^{i}) (({\boldsymbol{\theta}}^{k} - {\boldsymbol{\theta}}^{k-1})^{\mathrm{T}}({\boldsymbol{\theta}}^{k} - {\boldsymbol{\theta}}^{k-1})) \mathrm{d} {\boldsymbol{\theta}}^{k-1} \mathrm{d} {\boldsymbol{\theta}}^{k} . \end{split} (10) Now we discuss how to evaluate (8)-(10). For P(r_{j}^{1} | {\varTheta}^{i}) and P(r_{j}^{k-1}, r_{j}^{k} | {\varTheta}^{i}) , it can be proved that
\begin{split} P(r_{j}^k = 1 | {\varTheta}^i) = {\varPhi}\left(\frac{{\boldsymbol{\alpha}}_{e^k_j}^{\mathrm{T}}\cdot ({\boldsymbol{\mu}}-{\boldsymbol{\beta}}_{e^k_j})}{||\{{\boldsymbol{\alpha}}_{e^k_j}\cdot ({\boldsymbol{\varSigma}}^i_{0} + (k-1){\boldsymbol{\varSigma}}^i)^{\tfrac{1}{2}}, - 1\}||_2}\right),\\ \end{split} (11) \begin{split} & P(r_{j}^{k-1}, r_{j}^{k} = 1| {\varTheta}^{i})\\ =& \int P({\boldsymbol{\theta}}^{k-1}|{\varTheta}^{i}) P(r_{j}^{k-1}| {\boldsymbol{\theta}}^{k-1}, {\varTheta}^{i})\times\\&{\varPhi}\left(\frac{{\boldsymbol{\alpha}}_{e^k_j}^{\mathrm{T}}\cdot ({\boldsymbol{\theta}}^{k-1}-{\boldsymbol{\beta}}_{e^k_j})}{||\{{\boldsymbol{\alpha}}_{e^k_j} \cdot [{\boldsymbol{\varSigma}}^i_{0} + (k-1){\boldsymbol{\varSigma}}^i]^{\tfrac{1}{2}}, - 1\}||_2}\right) \mathrm{d} {\boldsymbol{\theta}}^{k-1}, \\[-1pt] \end{split}\ \ (12) where e^k_j is the k -th exercise in the j -th record, {\boldsymbol{\alpha}}_{e^k_j},\ {\boldsymbol{\beta}}_{e^k_j} are corresponding discrimination and difficulty vectors, respectively, and {\boldsymbol{\varSigma}}^i_{0},\ {\boldsymbol{\varSigma}}^i are parameters obtained after iteration i-1 . Term \{{\boldsymbol{\alpha}}_{e^k_j}\cdot ({\boldsymbol{\varSigma}}^i_{0}+ (k-1){\boldsymbol{\varSigma}}^i)^{{1}/{2}},-1\} is a vector obtained by the concatenation of vector {\boldsymbol{\alpha}}_{e^k_j}\cdot ({\boldsymbol{\varSigma}}^i_{0}+(k-1){\boldsymbol{\varSigma}}^i)^{{1}/{2}} and value -1 . For the integral term in (8)-(10), it is easy to prove that the prior distribution P({\boldsymbol{\theta}}^{k}| {\varTheta}^{i}) of {\boldsymbol{\theta}}^k is {\cal{N}}({\boldsymbol{\mu}}^i, (k-1){\boldsymbol{\varSigma}}^i + {\boldsymbol{\varSigma}}^i_0) . Based on this property, we take samples from the prior distribution of {\boldsymbol{\theta}}^k to evaluate (8) and (9), and samples from the joint distribution of \{{\boldsymbol{\theta}}^{k-1},{\boldsymbol{\theta}}^k\} to evaluate (10) approximately. In addition, summing all historical records R_j in D is expensive due to the different lengths of R_j , and thus we sample different batches of R_j during each training iteration.
So far we have illustrated how to maximize L_1,\ L_2 to update {\boldsymbol{\mu}},\ {\boldsymbol{\varSigma}}_0,\ {\boldsymbol{\varSigma}} . For \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q\} , there is no closed-form solution of L_3 , and thus we perform stochastic gradient descent (SGD)[54] to optimize \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q\} iteratively. Specifically, the derivatives of \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q\} for exercise q are:
\begin{split} &\nabla_{{\boldsymbol{\alpha}}_q}\\ =& \displaystyle\sum\limits_{R_j}\displaystyle\sum\limits_{k = 1}^{t_{j}}\frac{{\cal{I}} \{e_{j}^{k} = q\}sign(r^k_j)}{P(r_{j}^{k}|{\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i)}\int P({\boldsymbol{\theta}}^k|{\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i)\times\\& \frac{P(r_{j}^{k}|{\boldsymbol{\theta}}^k, {\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i)}{P(r_{j}^{k}|{\boldsymbol{\theta}}^k, {\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q)} \mathrm{exp}\left(-\frac{1}{2}({\boldsymbol{\alpha}}_q^{\mathrm{T}}({\boldsymbol{\theta}}^k-{\boldsymbol{\beta}}_q))^{2}\right)\times\\ &({\boldsymbol{\theta}}^k - {\boldsymbol{\beta}}_q)\mathrm{d} {\boldsymbol{\theta}}^k, \end{split} (13) \begin{split} & \nabla_{{\boldsymbol{\beta}}_q} \\= &\sum\limits_{R_j}\sum\limits_{k = 1}^{t_{j}}\frac{{\cal{I}}\{e_{j}^{k} = q\}{sign}(r^k_j)}{P(r_{j}^{k}|{\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i)}\int P({\boldsymbol{\theta}}^k|{\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i)\times\\& \frac{P(r_{j}^{k}|{\boldsymbol{\theta}}^k, {\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i)}{P(r_{j}^{k}|{\boldsymbol{\theta}}^k, {\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q)} \mathrm{exp}\left(-\frac{1}{2}[{\boldsymbol{\alpha}}_q^{\mathrm{T}}({\boldsymbol{\theta}}^k-{\boldsymbol{\beta}}_q)]^{2}\right)\times\\ &(-{\boldsymbol{\alpha}}_q)\mathrm{d} {\boldsymbol{\theta}}^k, \end{split} (14) where {\cal{I}} \{e_{j}^{k} = q\} is an indicator function that equals 1 if exercise e_{j}^{k} is exercise q , and 0 otherwise, {sign}(r^k_j) is a sign function that equals 1 if result r_{j}^{k} is 1 (a student answered correctly), and -1 otherwise, and {\boldsymbol{\alpha}}_q^i, {\boldsymbol{\beta}}_q^i are parameters obtained after iteration i-1 in the EM algorithm, and are fixed when using SGD to optimize L_3 during iteration i . In summary, for the M-step in the EM algorithm, we combine (8)-(12) and adopt sampling to update {\boldsymbol{\mu}},\ {\boldsymbol{\varSigma}}_0,\ {\boldsymbol{\varSigma}} , and utilize SGD to update \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q|q = 1,2,\ldots,M\} based on (13) and (14).
3.4 Model Inference
After the training phrase and acquiring parameters {\varTheta} , our goal turns to diagnose (infer) a student's proficiency at time T+1 , denoted as {\boldsymbol{\theta}}^{T+1} , given his/her records S = \{s^1,s^2,\ldots,s^T|s^t = (e^t, r^t)\} . Specifically, we formulate the maximum posterior distribution of {\boldsymbol{\theta}}^{T+1} by the Bayesian law as follows:
P({\boldsymbol{\theta}}^{T+1}|S, {\varTheta})\propto P(S|{\boldsymbol{\theta}}^{T+1}, {\varTheta})P({\boldsymbol{\theta}}^{T+1}|{\varTheta}). (15) Computing P(S|{\boldsymbol{\theta}}^{T+1}, {\varTheta}) is expensive, and thus we use the following approximation proposed in TIRT[24]:
\begin{split} & P(S |{\boldsymbol{\theta}}^{T+1}, {\varTheta})\\ \approx & \prod\limits_{k = 1}^{T} P(r^{k}| {\boldsymbol{\theta}}^{T+1}, {\varTheta}) \\ = & \prod\limits_{k = 1}^{T} \widetilde{p}_{k}^{r^{k}}(1-\widetilde{p}_{k})^{1-r^{k}},\end{split} (16) where
\widetilde{p}_{k} = {\varPhi}\left(\dfrac{{\boldsymbol{\alpha}}_{e^k}^{\mathrm{T}}\cdot ({\boldsymbol{\theta}}^{T+1}-{\boldsymbol{\beta}}_{e^k})}{||\{{\boldsymbol{\alpha}}_{e^k}\cdot ((T+1-k){\boldsymbol{\varSigma}})^{{1}/{2}},-1\}||_2}\right), and {\boldsymbol{\alpha}}_{e^k},\ {\boldsymbol{\beta}}_{e^k} are discrimination and difficulty vectors of exercise e^k answered at time k respectively. Note that the further back in time the response is, the smaller || \nabla_{{\boldsymbol{\theta}}^{T+1}} \widetilde{p}_{k} ||_2 is and thus the lower the influence it has on maximizing (16), i.e., inferring {\boldsymbol{\theta}}^{T+1} , by a gradient-based method like SGD. Therefore, UTIRT treats records differently, and focuses more on the latest records (e.g., e_3,\ e_4 in Fig.1). Combining (15) and (16), we have the log-posterior:
\begin{split} &\ln P({\boldsymbol{\theta}}^{T+1}|S, {\varTheta})\propto \ln P({\boldsymbol{\theta}}^{T+1}|{\varTheta}) +\\&\qquad \sum\limits_{k = 1}^{T}(r^{k} \ln \widetilde{p}_{k} + (1-r^{k})\ln (1-\widetilde{p}_{k})). \end{split} Compared with MIRT, UTIRT has an additional term in the inferencing phase, i.e., \ln P({\boldsymbol{\theta}}^{T+1}|{\varTheta}) , which describes the Gaussian prior of {\boldsymbol{\theta}}^{T+1} and can be seen as a regularization. Thus the general form of the loss function to be minimized in the inferencing phase is:
\begin{split} Loss = &-\Bigg(\sum\limits_{k = 1}^{T} (r^{k} \ln \widetilde{p}_{k} + (1-r^{k})\ln (1-\widetilde{p}_{k}))+ \\& {\lambda} \ln P({\boldsymbol{\theta}}^{T+1}|{\varTheta})\bigg). \end{split} (17) It is worth noting that the loss in (17) keeps a balance between score prediction loss and prior distribution loss with the hyper-parameter {\lambda} , which will be explored further in Section 4.
3.5 Relation with Other CD Models
In this subsection, we discuss the relationship between UTIRT and classic CD models and show that UTIRT is a general framework that covers many traditional models: IRT[7], MIRT[8], and TIRT[9].
IRT. Take the typical 2PO model f(\boldsymbol \theta; q) = {\varPhi}[\boldsymbol\alpha_q\cdot (\boldsymbol \theta-\boldsymbol \beta_q)] as an example. In (1), we set {\boldsymbol \varSigma} = 0 and let \boldsymbol \theta be unidimensional, and then a student's proficiency is an invariant value, which is the underlying assumption of IRT. Moreover, assuming {\boldsymbol \varSigma}_0 equals infinite and \mu is any value, the Gaussian hypothesis of initial proficiency \boldsymbol \theta^1 is deprecated, the learning phase (5) becomes classic marginal maximum likelihood estimation (MMLE) for IRT and the inferencing phase becomes maximum likelihood estimation (MLE).
MIRT. MIRT is a direct extension of IRT by using multidimensional latent vectors of exercises and students. The typical 2PO form is described in (3). {\boldsymbol{\varSigma}} in (1) is set as a zero matrix, and then students' proficiency is seen unchanged over time. Similar to IRT, let {\boldsymbol{\varSigma}}_0 be a matrix whose elements are infinite, and {\boldsymbol{\mu}} be any vector, the learning method degrades into MMLE for MIRT proposed in [55] and the inferencing method becomes MLE proposed in [56].
TIRT. TIRT can be seen as a compromise between IRT and UTIRT. It is a unidimensional model and trains exercise parameters \boldsymbol \alpha_q,\ \boldsymbol \beta_q by a standard IRT. Only in the inferencing phase, temporality and randomness are considered, and the evolution of students' proficiency is modeled as a Wiener process whose variance is a hyper-parameter. If \boldsymbol \mu,\ {\boldsymbol\varSigma}_0,\ {\boldsymbol\varSigma} are fixed in (1) (as hyper-parameters) and \boldsymbol \theta is set to be unidimensional, UTIRT is equivalent to TIRT because the training phase in (7) only needs to learn the exercise parameters of IRT, and the inferencing phase in (17) is Maximum a Posterior Estimation adopted similar to TIRT. Therefore, TIRT is a simplified version of UTIRT.
4. Experiments
In this section, we conduct three experiments on two real-world datasets to evaluate the effectiveness of our proposed framework and its implementations from various aspects: 1) knowledge proficiency estimation performance of UTIRT against the baselines; 2) the comparison of next score prediction results between UTIRT and baselines; 3) the analysis of utilizing temporality in UTIRT and TIRT.
4.1 Dataset Description
We use two real-world datasets in the experiments, i.e., ASSIST and Junyi. ASSIST (ASSISTments 2009–2010 “skill builder”) is an open dataset collected by the ASSISTments online tutoring system[57], which contains student response logs and knowledge concepts on mathematical exercises. Junyi was collected from an E-learning platform called Junyi Academy, which provides the problem logs and exercise-related information[58].
As for ASSIST, we choose the public corrected version that eliminates the duplicated data and preprocess as follows. 1) Inspired by [9], we associate exercises not aligned with a skill with a “dummy” skill. 2) The dataset records the order of students’ exercise history. Since our model utilizes temporality of proficiency and treats historical records differently according to their order, we sort each student’s answering trajectory with the given “order_id” provided in the dataset.
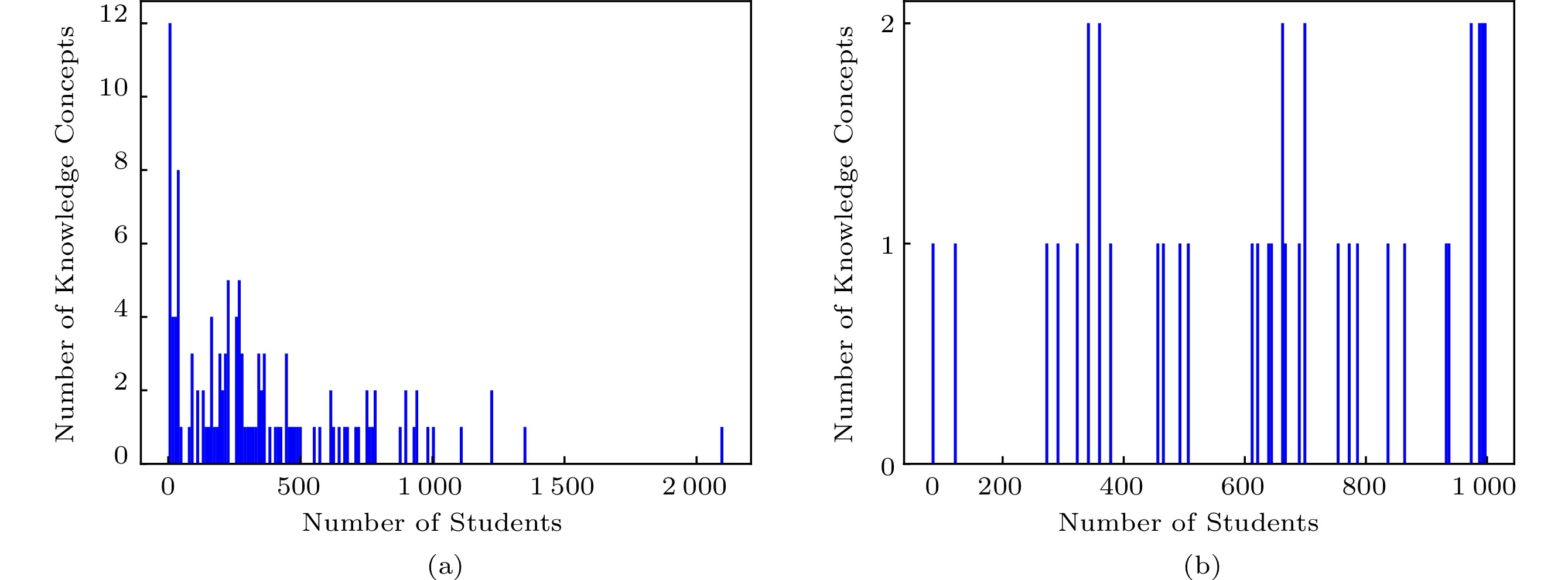
As for Junyi, we make the following preprocessing. 1) As the tutor system of Junyi Academy only records a student's first response to the same exercise, and the response will be marked “wrong” if any hint is requested[58], we just take their first-attempt responses as the true records. 2) Similar to [59], we select 1\ 000 most active learners from the exercise logs to yield the dataset. 3) Exercises in the Junyi dataset are associated with a “topic”, which is viewed as the corresponding knowledge concept in our experiment. To have a better comparison with [59], different from ASSIST, exercises without a “topic” are discarded. 4) We sort each student's records with the given UNIX timestamp. The statistics of the datasets after preprocessing are summarized in Table 1, and the distribution of students' historical records is shown in Fig.3.
Table 1. Statistics of the Two DatasetsDataset #Students #Exercises #Knowledge Concepts #Response Logs Avg. Exercising Records per Student Avg. Knowledge Concepts per Exercise Avg. Exercises per Knowledge Concept ASSIST[57] 4 217 26 683 124 346 852 82.251 1.131 243.371 Junyi[58] 1 000 712 39 203 945 203.945 1.000 18.256 Note: “ \# ” denotes “the number of”, and “Avg.” denotes “the average number of”. 4.2 Experimental Setup
4.2.1 Parameters Setting
With regard to the EM algorithm in the training phase, the number of epochs is 50 , and the mini-batch is 256 and 128 in ASSIST and Junyi, respectively. We initialize {\boldsymbol{\mu}} , {\boldsymbol{\alpha}}_q , {\boldsymbol{\beta}}_q , {\boldsymbol{\varSigma}}_0 , {\boldsymbol{\varSigma}} with Xavier initialization[60]. When optimizing L_3 by (13) and (14) to learn \{{\boldsymbol{\alpha}}_q, {\boldsymbol{\beta}}_q\} , we set learning rate to 0.001 and epoch as 20 . In the inferencing phase, {\lambda} is set to 0.1 in (17), the epoch number is set to 50 , and the learning rate is set to 0.001 .
4.2.2 Comparison Approaches
To evaluate the performance of our UTIRT, we compare it with previous approaches, i.e., IRT, MIRT, TIRT, LFM, PFA, PMF, NeuralCD, BKT, DKT, and DKT-KC. The details of them are as follows.
● IRT [7]. IRT is a CD method modeling a student's proficiency, exercise parameters, and answers by a logistic-like function.
● MIRT [8]. MIRT is a direct extension of IRT, using multidimensional latent trait vectors of exercises and students, and predicts results by (3).
● TIRT [9]. TIRT is also an extension of IRT, modeling students' proficiency as a stochastic process varying over time. However, it trains parameters by an IRT model, thus considering temporality only in the inferencing phase.
● LFM [23]. LFM can be seen as a special version of IRT that only utilizes the difference between students' proficiency and exercise difficulty.
● PFA [27]. PFA is a logistic regression method that utilizes the frequency of previous successes and failures associated with each skill.
● PMF [12]. PMF is a probabilistic matrix factorization method that represents students and exercises by low-dimensional latent vectors.
● NeuralCD [4]. NeuralCD is a neural CD model, which uses neural networks to model complex interactions between exercises and students.
● BKT [38]. BKT is a hidden Markov model that represents each student's knowledge states as a set of binary variables.
● DKT [47]. DKT is a representative deep learning based model that leverages recurrent neural networks to model a student's knowledge state with a hidden vector during the learning process. However, to the best of our knowledge, traditional DKT does not incorporate the knowledge components of exercises, and thus it is unsuitable for the scenario with multiple knowledge concepts. Therefore, we adopt its original RNN architecture and make a little change by adding one full-connected layer to the DKT output layer. With this adjustment, DKT can predict the result of an exercise based on the mastery probability of knowledge components.
● DKT-KC[10]. DKT-KC is a variation of DKT, which inputs the knowledge components (KC) related to the exercises identified by Q-matrix[10].
In the following experiments, all models are implemented by ourselves using Python. We conduct all experiments on a Linux server with four 2.0 GHz Intel Xeon E5-2620 CPUs and a Tesla K80m GPU. For fairness, all parameters in these baselines are tuned to have the best performances.
4.3 Experimental Results
4.3.1 Knowledge Proficiency Estimation
The first experiment is to evaluate the effectiveness of our model in diagnosing students' knowledge states, which is the goal of CD, and to prove the importance of utilizing temporality and randomness. As there is no ground truth of students' proficiency, we adopt a score prediction task to indirectly evaluate the performances of models[4, 12, 24, 25, 61], because [62] has pointed out that differences between the observed scores and the predicted scores can be used to examine if there is any biased estimation pattern. Therefore, it is reasonable to assume there is a positive correlation between students' proficiency and the probability of answering correctly, and accurate prediction always implies accurate diagnosis. Considering that all exercises are objective ones, we use evaluation metrics from both the classification aspect and the regression aspect, including RMSE (root mean square error), ACC (accuracy), and AUC (area under the curve).
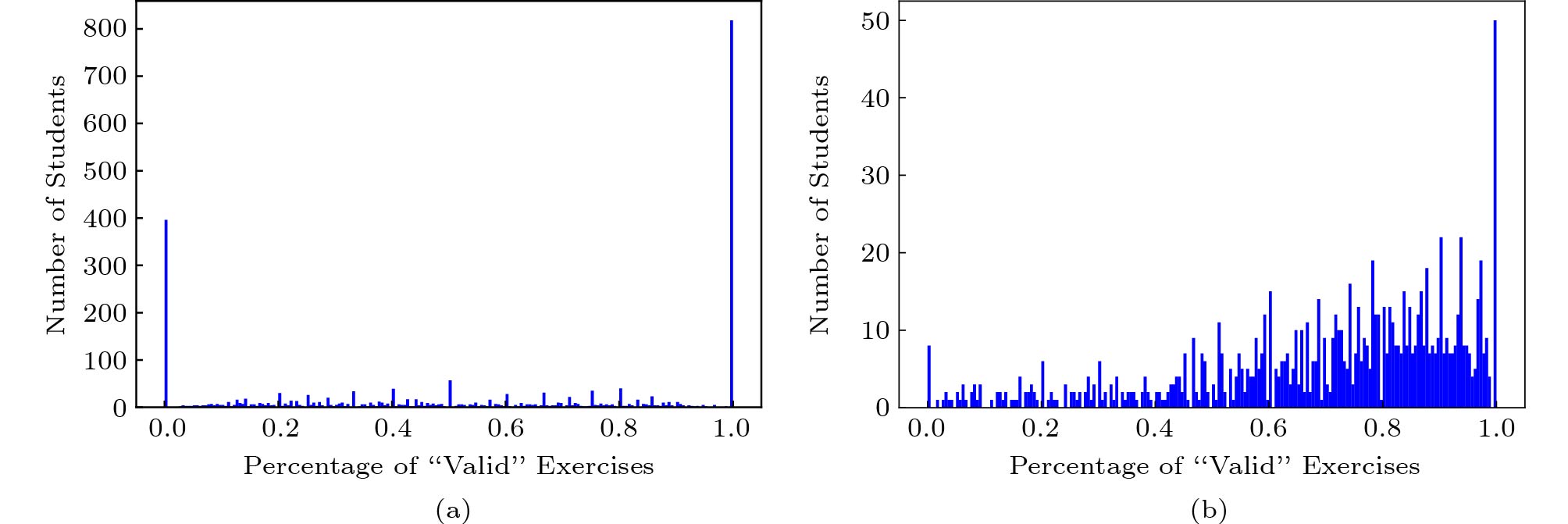
Since we could hardly capture the change of a student's proficiency accurately if he/she just finished few exercises in the past, for ASSIST, we further discard the “dummy skill” and filter out students with less than 15 response logs, which was done in [4]. For Junyi, since we have selected the most 1\ 000 active students, there is no need to filter students with few records. After pre-processing, ASSIST consists of 2\ 500 students, 17\ 671 exercises and 123 knowledge concepts, and Junyi consists of 1\ 000 students, 712 exercises and 39 knowledge concepts. To better illustrate the data, we calculate for each student the percentage of exercises in the test data containing enough (more than 50 %) knowledge concepts that occur in training data, and such exercises are named “Valid”. Fig.4 shows the results of all students. From Fig.4, we find that in both ASSIST and Junyi, many students have invalid exercises which are related to the knowledge concepts they have not experienced in the training data, and it will bring the challenge of diagnosing proficiency on these concepts.
![]() Figure 4. Statistics of “Valid” exercises in Subsection 4.3.1. (a) ASSIST. (b) Junyi.
Figure 4. Statistics of “Valid” exercises in Subsection 4.3.1. (a) ASSIST. (b) Junyi.In this experiment, we perform a 70 %/ 10 %/ 20 % training/validation/test split of students' response logs, using each student's first 70 % data to train parameters. Then, we infer each student's proficiency {\boldsymbol{\theta}}^{\rm T} after finishing his/her training records, and predict scores on his/her test (last 20 %) data by using {\boldsymbol{\theta}}^{\rm T} . We select all the baselines mentioned above.
Table 2 shows the experimental results of all models, and there are several observations. Firstly, UTIRT performs the best ACC and equivalent RMSE, AUC on all datasets, followed by MIRT, NeuralCD and LFM, which indicates the effectiveness of our framework in estimating knowledge proficiency by incorporating students' dynamic learning process (i.e., temporality and randomness). Secondly, UTIRT and TIRT, as two dynamic models, perform better than their traditional static forms (MIRT, IRT) in ASSIST, and UTIRT is also better in Junyi, which demonstrates that it is more effective to track students' proficiency from a temporal perspective. Meanwhile, they achieve better results than PFA, BKT, DKT and DKT-KC, further proving the superiority of considering randomness. Thirdly, we observe that TIRT performs worse than IRT in Junyi. This may result from the greater effect of temporality in Junyi, which is shown in Table 1, where the average number of students' historical records in Junyi is larger than that in ASSIST. With the influence of temporality increasing, the conflict of utilizing temporality differently in the training and inferencing phase is manifest, and it causes even worse predictive results of TIRT. This observation demonstrates the importance of unified training and inferencing methods, which will be further illustrated in Subsection 4.3.3. Fourthly, NeuralCD does not perform so well as stated in [4], especially in Junyi. This is mainly because the data partition method we adopt (split data chronologically) is different from the method adopted in [4] (shuffle data before splitting), and this causes much more “invalid” exercises (see Fig.4). To be more specific, as NeuralCD diagnoses a student's proficiency on different knowledge concepts independently due to incorporating Q-matrix in exercise factors, the predictions of his/her scores are unreliable on exercises containing knowledge concepts that did not appear in his/her training data (i.e., invalid exercises). Contrarily, UTIRT does not suffer from this problem because it learns the correlations between different knowledge concepts by the covariance matrix {\boldsymbol{\varSigma}} . As a result, even if a student has never answered exercises related to a specific knowledge concept k , UTIRT can still infer his/her state on k based on states of other knowledge concepts and their correlations with k . Probably for the same reason, PFA, BKT, DKT and DKT-KC do not perform well either, which proves UTIRT's advantage of utilizing the relationships between different knowledge concepts. Lastly, DKT-KC performs better than BKT and DKT, indicating the effectiveness of complex student modeling and the incorporation of knowledge components.
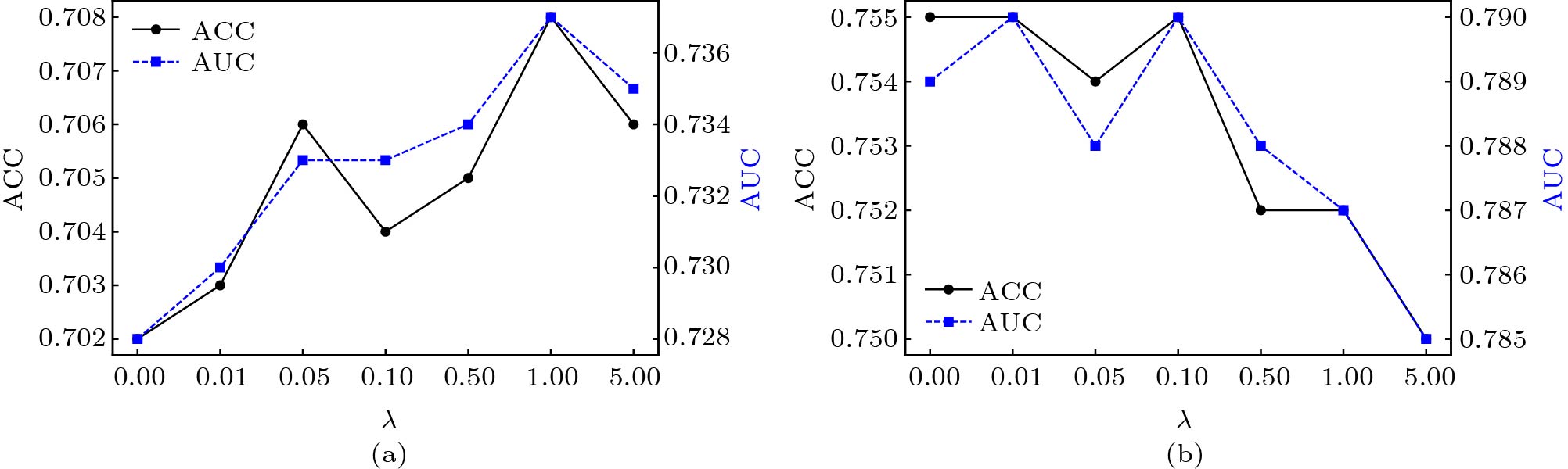
Table 2. Knowledge Proficiency Estimation PerformanceModel ASSIST Junyi RMSE ACC AUC RMSE ACC AUC IRT[7] 0.493 0.668 0.667 0.417 0.742 0.799 MIRT[8] 0.482 0.694 0.730 0.416 0.747 0.800 TIRT[9] 0.488 0.669 0.672 0.421 0.735 0.798 LFM[23] 0.456 0.682 0.697 0.422 0.733 0.787 PFA[27] 0.460 0.672 0.671 0.465 0.658 0.672 PMF[12] 0.503 0.662 0.717 0.448 0.721 0.767 NeuralCD[4] 0.454 0.686 0.703 0.438 0.707 0.755 BKT[38] 0.488 0.658 0.679 0.466 0.654 0.662 DKT[47] 0.487 0.636 0.619 0.441 0.703 0.743 DKT-KC[10] 0.461 0.671 0.665 0.425 0.734 0.782 UTIRT 0.469 0.704 0.733 0.414 0.755 0.790 Note: The best results are in bold. Parameter Sensitivity. We now discuss the sensitivity of parameter {\lambda} in (17). {\lambda} is the regularization parameter controlling the deviation from students' proficiency at time T+1 to its prior distribution. Fig.5 visualizes the performances with increasing values of {\lambda} = 0,0.01,0.05,0.10,0.50,1.00,5.00 in ASSIST and Junyi. As we can see from Fig.5, different datasets show different results. As {\lambda} increases, the performance of UTIRT increases at first and reaches the peak when {\lambda} = 1.00 in ASSIST, while it keeps decreasing in Junyi.
4.3.2 Next Score Prediction
To further prove the effectiveness of UTIRT for the knowledge tracing task, we predict students' scores step by step, which was adopted in [9, 25, 47, 48, 59]. In practice, we can provide personalized exercise recommendations for students based on the prediction results, saving their time on practicing too hard/easy exercises. Different from Subsection 4.3.1, with trained UTIRT, for each time t , we minimize (17) on each student's first t-1 interactions to diagnose his/her proficiency {\boldsymbol{\theta}}^{t} at time t and then predict whether or not the student answers a specific exercise at time t correctly. RMSE, ACC and AUC are used to evaluate performance.
Similar to [9], we filter out students with less than two response logs. As a result, there are 4 097 students, 26 679 exercises and 124 knowledge concepts in ASSIST, and Junyi is the same as mentioned in Subsection 4.3.1. To better understand each dataset, we calculate the number of students per knowledge concept as [63] did. Fig.6 shows that in ASSIST, most of the knowledge concepts appear in the histories of no more than 500 students, while in Junyi, about two thirds of knowledge concepts occur in the records of more than 500 students. It reflects different generalization of each dataset[63], and we will see in our experiment that it leads to different effects of fitting models and predictive performances.
![]() Figure 6. Statistics of datasets in Subsection 4.3.2. (a) ASSIST. (b) Junyi.
Figure 6. Statistics of datasets in Subsection 4.3.2. (a) ASSIST. (b) Junyi.In this experiment, we set the logs of 80% students as training data and 20% as test data. All the baselines mentioned in Subsection 4.2.2 are selected for comparison except LFM, PMF and NeuralCD because they are unsuitable for knowledge tracing scenarios.
Table 3 shows the overall results of all models for predicting student scores. From Table 3, we can observe that UTIRT outperforms almost all the other baselines on both datasets, followed by MIRT in ASSIST and DKTs (DKT and DKT-KC) in Junyi, indicating the effectiveness of our model in tracing students' learning processes. Moreover, UTIRT and TIRT still perform better than MIRT and IRT, respectively, which demonstrates that it is effective to incorporate temporality into modeling. Besides, UTIRT outperforms PFA, BKT, DKT and DKT-KC in ASSIST and Junyi. This observation indicates that describing the knowledge state evolving by a probabilistic graph (i.e., utilizing randomness) is more suitable to trace students' proficiency. An interesting finding is that DKTs, although leveraging deep neural networks for modeling, perform unsatisfactorily in ASSIST. This may be because our data volume does not support DKTs. On the one hand, deep models usually have too many parameters to be optimized, especially in our experiments, where we add one dense layer and bring more parameters proportional to the number of exercises and concepts. On the other hand, as [63] points out, the number of students per knowledge concept in ASSIST (Fig.6) is too small to attain the effective size, and thus DKTs may overfit and lack generalization ability. In summary, all evidence demonstrates the effectiveness and rationality of the proposed factors in our framework (i.e., temporality and randomness).
Table 3. Next Score Prediction PerformanceModel ASSIST Junyi RMSE ACC AUC RMSE ACC AUC IRT 0.415 0.724 0.754 0.410 0.750 0.772 MIRT 0.422 0.730 0.754 0.412 0.747 0.770 TIRT 0.412 0.728 0.762 0.411 0.749 0.771 PFA 0.450 0.704 0.647 0.431 0.729 0.698 BKT 0.443 0.711 0.671 0.432 0.726 0.694 DKT 0.464 0.648 0.670 0.407 0.752 0.773 DKT-KC 0.441 0.697 0.719 0.408 0.753 0.773 UTIRT 0.408 0.747 0.769 0.410 0.758 0.774 Note: The best results are in bold. 4.3.3 Temporality Utilization Analysis
Now we aim to demonstrate the superiority of UTIRT in leveraging temporality theoretically and practically to TIRT. As mentioned before, TIRT trains a standard IRT to get difficulty and discrimination parameters of exercises, ignoring temporality, while introducing dynamics of students' proficiency in the inferencing phase. We conduct hypothesis testing to theoretically prove the existence of a contradiction between its training and inferencing phase. Besides, we investigate the degree to which the temporal structure in data affects the predictive performance of TIRT and UTIRT, further verifying UTIRT's effectiveness. The data from Subsection 4.3.2 are also used in this experiment.
We first adopt the hypothesis test of “the relationship between students proficiency diagnosed by IRT in consecutive moments obeys the Gaussian distribution”. If the test result rejects this assumption, we could conclude that: the training phase in TIRT implicitly rejects the Gaussian hypothesis of students' proficiency evolving. Nevertheless, it still utilizes the Gaussian hypothesis in the inferencing phase, and thus TIRT uses contradictory training and inferencing methods. With respect to the process of hypothesis test, we train an IRT model and infer students' proficiency at each time by IRT. After that, we calculate the difference in discovered proficiency between two consecutive moments. Then, we do the Kolmogorov-Smirnov test[64] to verdict on whether these values obey the Gaussian distribution. To avoid the influence of sample size, we shuffle these values, then take 100 samples as a batch to repeat the test, and calculate the average p-value.
The p-value for ASSIST and Junyi is 4.61\times 10^{-6} and 6.08\times 10^{-3} , respectively, both smaller than the significance level of 0.05 , thus rejecting the hypothesis. In conclusion, the IRT model implicitly assumes that the process of students' proficiency change does not follow the Gaussian distribution. Therefore, if we model temporality only in the inferencing phase (as TIRT does), it will cause a contradiction between the training hypothesis and the inferencing hypothesis. It further shows the importance of a unified training and inferencing framework and proves UTIRT's priority to TIRT.
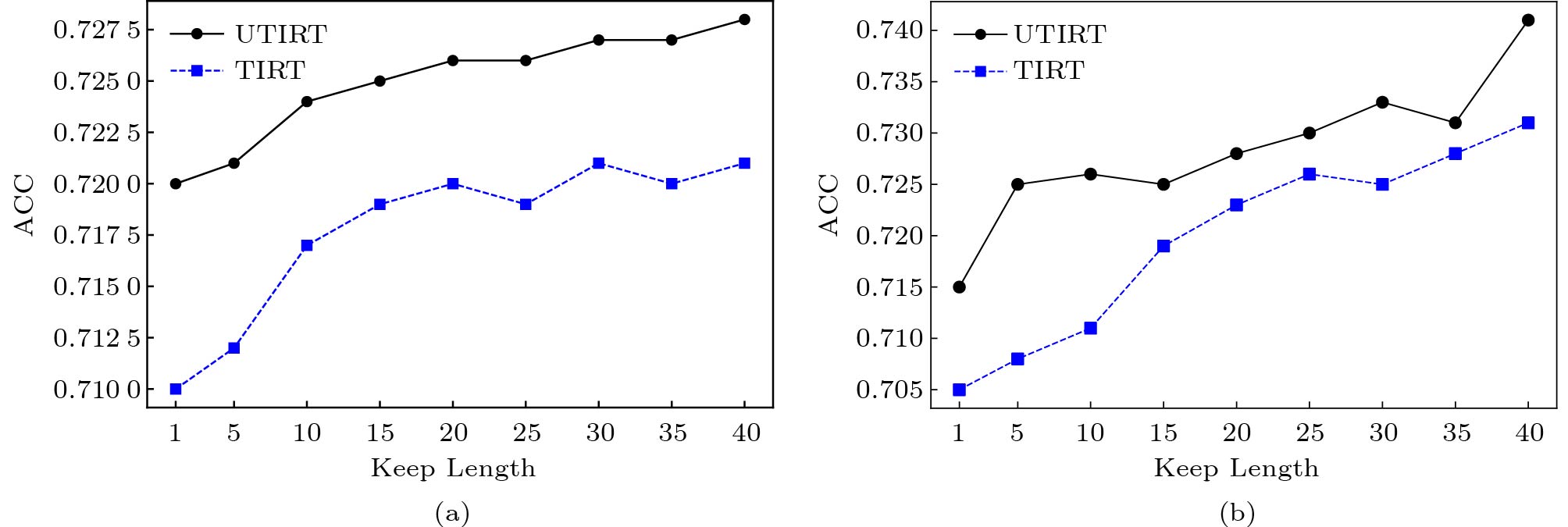
Second, to better compare UTIRT with TIRT and illustrate our framework's advantage in leveraging temporality, we conduct an experiment on how “keep length” influences the predictive accuracy. To be more specific, given a student's answering sequence in test data, we choose the first “keep length” records to infer his/her knowledge state and then use the diagnosed result to predict scores on the last 20% of exercises. For example, if “keep length” is set to 5 and there are 50 records in a student's logs, we use the first five records to diagnose his/her proficiency, based on which we predict answers on the last 10 exercises. Fig.7 shows the performances with “keep length” growing from 1 to 40. As “keep length” could be 40, we need to ensure a student's last 20% records are not included in the first 40 records, and therefore only students with more than 50 records are selected in this experiment.
We can see that the greater the “keep length”, the higher the predictive accuracy. That is probably because with “keep length” increasing, we have more data closer to the test record, which better reflects a student's current knowledge state. Therefore, the result shows the necessity of considering the order of the response sequence and proves that the latest history is more important than the previous one. What is more, UTIRT performs better than TIRT with any “keep length”, indicating that UTIRT can better capture and utilize the temporality of students' proficiency. Based on this evidence and the result of hypothesis test above, we can conclude that UTIRT is more credible in theory and can better model the temporality of students' knowledge states than TIRT.
5. Discussion
In this section, we comprehensively discuss the advantages of our work and some possible research directions in the future. In this paper, we illustrate the problem of modeling temporality and randomness when diagnosing students' knowledge states. We propose a probabilistic graphical model that incorporates a Wiener hypothesis to describe the evolving process of students' proficiency. To reduce the computational complexity in the learning phase, we propose another hypothesis based on the relationship between students' ability and answering scores. Both hypotheses are interpretable and explain the change of students' knowledge proficiency. Although we can observe that UTIRT provides accurate results for knowledge state diagnosis and student scores prediction, there are still some directions for future studies.
First, the simplicity of the Wiener hypothesis which is used to describe the change of students' proficiency may hinder our framework to model more complex situations. Besides, students' psychological factors and exercises' characteristics also affect the response results. Therefore, it would be valuable to explore more flexible methods to trace the students' proficiency, such as educational theories, psychological traits (e.g., slip, guess, forget and learn[50], gaming factor[65], behavior patterns[66, 67] and learning style[68]), other temporal aspects (e.g., exercise difficulty and discrimination, resource properties) and neural networks.
Second, our work focuses more on the dynamic evolution of students' general proficiency and has not been explicitly related to specific knowledge concepts. We may make our efforts to incorporate the interaction between each knowledge concept and mastery degree by using Q-matrix as [4] did, which can provide diagnosis results on each concept and is useful for further applications, such as recommending specific exercises to help students improve their performances on targeted knowledge[69].
Third, we just exploit the performance data of students. In practice, there are plenty of other important data that can help us with modeling. For example, to model the impact between different concepts, we can leverage their prerequisite relationships described by knowledge graph[70, 71] and utilize graph neural networks for their great power in graph representation[72]. What is more, students have a number of attempts when answering an exercise on an online platform and can seek help (“hints”), which can be used to model their knowledge acquisition. For instance, some previous work[65, 73, 74] pay attention to multiple attempts, and combine knowledge and gaming for student learning modeling[65], while [75–77] consider hints into the learning process. Actually, it is interesting to exploit more students' behaviors (e.g., the number of attempts, submission patterns or hints) for modeling. For instance, if the time interval between two attempts is too short, the student's ability changes rarely, which can be described by the covariance matrix in the Wiener process. In addition, a hint parameter can be introduced as a supplement to a student's proficiency, and therefore we are able to filter its impact on response results, thus correctly diagnosing proficiency. Moreover, clock time that represents the exact timestamp of each response in reality may implicitly reflect the student's proficiency[49]. These data could be potentially helpful for CD.
Last, from a broader perspective, UTIRT aims at diagnosing users' states (in our case, students' proficiency) from their historical records, and we are willing to extend it to other fields, such as diagnosing consumers' preferences in e-commerce and players' ability in computer games. We believe that our model has the potential to work effectively on such problems with strong temporality.
6. Conclusions
In this paper, we focused on dynamically diagnosing students' knowledge states and proposed a probabilistic graphical model based UTIRT framework. UTIRT models the temporality and randomness of students' proficiency evolving by a Wiener hypothesis and achieves tractable maximization (M-step) in the EM algorithm for training with another hypothesis describing the relationship between the exercising records and students' proficiency at time k . UTIRT contains unified training and inferencing phases and could be seen as the generalization of some traditional CD models. Three experiments on two real-world datasets, i.e., knowledge proficiency estimation, next score prediction, and temporality utilization analysis, confirmed the effectiveness of our framework. Experimental results showed that both temporality and randomness considered in UTIRT are important to get better diagnosis accuracy (ACC, AUC) and lower error rate (RMSE). Moreover, the unified training and inferencing phases make UTIRT more reasonable from both theoretical analyses and experimental performances. For future research, we would like to explore more possible factors in the learning process, such as multiple attempts, hints and clock time. The framework of our work and related results should benefit the development of online learning systems. We hope this work could inspire further studies.
-
Figure 1. Example of students' exercising records. (a) Exercises e1 to e4 with the same knowledge concept “greatest_common_divisor”. (b) Probability density function of s1’s and s2’s proficiency distribution: the y axis is the proficiency value (ranging from 0 to 1) and the x axis is the corresponding probability density. (c) Diagnosis results: 0.7 and 0.2 for s1 and s2 respectively.
Figure 4. Statistics of “Valid” exercises in Subsection 4.3.1. (a) ASSIST. (b) Junyi.
Figure 6. Statistics of datasets in Subsection 4.3.2. (a) ASSIST. (b) Junyi.
Table 1 Statistics of the Two Datasets
Dataset #Students #Exercises #Knowledge Concepts #Response Logs Avg. Exercising Records per Student Avg. Knowledge Concepts per Exercise Avg. Exercises per Knowledge Concept ASSIST[57] 4 217 26 683 124 346 852 82.251 1.131 243.371 Junyi[58] 1 000 712 39 203 945 203.945 1.000 18.256 Note: “ \# ” denotes “the number of”, and “Avg.” denotes “the average number of”. Table 2 Knowledge Proficiency Estimation Performance
Model ASSIST Junyi RMSE ACC AUC RMSE ACC AUC IRT[7] 0.493 0.668 0.667 0.417 0.742 0.799 MIRT[8] 0.482 0.694 0.730 0.416 0.747 0.800 TIRT[9] 0.488 0.669 0.672 0.421 0.735 0.798 LFM[23] 0.456 0.682 0.697 0.422 0.733 0.787 PFA[27] 0.460 0.672 0.671 0.465 0.658 0.672 PMF[12] 0.503 0.662 0.717 0.448 0.721 0.767 NeuralCD[4] 0.454 0.686 0.703 0.438 0.707 0.755 BKT[38] 0.488 0.658 0.679 0.466 0.654 0.662 DKT[47] 0.487 0.636 0.619 0.441 0.703 0.743 DKT-KC[10] 0.461 0.671 0.665 0.425 0.734 0.782 UTIRT 0.469 0.704 0.733 0.414 0.755 0.790 Note: The best results are in bold. Table 3 Next Score Prediction Performance
Model ASSIST Junyi RMSE ACC AUC RMSE ACC AUC IRT 0.415 0.724 0.754 0.410 0.750 0.772 MIRT 0.422 0.730 0.754 0.412 0.747 0.770 TIRT 0.412 0.728 0.762 0.411 0.749 0.771 PFA 0.450 0.704 0.647 0.431 0.729 0.698 BKT 0.443 0.711 0.671 0.432 0.726 0.694 DKT 0.464 0.648 0.670 0.407 0.752 0.773 DKT-KC 0.441 0.697 0.719 0.408 0.753 0.773 UTIRT 0.408 0.747 0.769 0.410 0.758 0.774 Note: The best results are in bold. -
[1] Guo X, Li R, Yu Q, Haake A R. Modeling physicians’ utterances to explore diagnostic decision-making. In Proc. the 26th International Joint Conference on Artificial Intelligence, Aug. 2017, pp.3700–3706. DOI: 10.24963/ijcai.2017/517.
[2] Yao C L, Qu Y, Jin B, Guo L, Li C, Cui W J, Feng L. A convolutional neural network model for online medical guidance. IEEE Access, 2016, 4: 4094–4103. DOI: 10.1109/ ACCESS.2016.2594839.
[3] Chen S, Joachims T. Predicting matchups and preferences in context. In Proc. the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2016, pp.775–784. DOI: 10.1145/2939672.2939 764.
[4] Wang F, Liu Q, Chen E H, Huang Z Y, Chen Y Y, Yin Y, Huang Z, Wang S J. Neural cognitive diagnosis for intelligent education systems. In Proc. the 34th AAAI Conference on Artificial Intelligence, Feb. 2020, pp.6153–6161. DOI: 10.1609/aaai.v34i04.6080.
[5] Kuh G D, Kinzie J, Buckley J, Bridges B K, Hayek J. Piecing together the student success puzzle: Research, propositions, and recommendations. ASHE Higher Education Report, 2007, 32(5): 1–182. DOI: 10.1002/aehe.3205.
[6] de la Torre J. Dina model and parameter estimation: A didactic. Journal of Educational and Behavioral Statistics, 2009, 34(1): 115–130. DOI: 10.3102/1076998607309474.
[7] Embretson S E, Reise S P. Item Response Theory. Psychology Press, 2013.
[8] Adams R J, Wilson M, Wang W C. The multidimensional random coefficients multinomial logit model. Applied Psychological Measurement, 1997, 21(1): 1–23. DOI: 10.1177/0146621697211001.
[9] Wilson K H, Karklin Y, Han B J, Ekanadham C. Back to the basics: Bayesian extensions of IRT outperform neural networks for proficiency estimation. arXiv: 1604.02336, 2016. https://arxiv.org/abs/1604.02336, Nov. 2023.
[10] Tatsuoka K K, Tatsuoka M M. Computerized cognitive diagnostic adaptive testing: Effect on remedial instruction as empirical validation. Journal of Educational Measurement, 1997, 34(1): 3–20. DOI: 10.1111/j.1745-3984.1997. tb00504.x.
[11] Leighton J P, Gierl M J, Hunka S M. The attribute hierarchy method for cognitive assessment: A variation on Tatsuoka’s rule-space approach. Journal of Educational Measurement, 2004, 41(3): 205–237. DOI: 10.1111/j.1745-3984.2004.tb01163.x.
[12] Thai-Nghe N, Horváth T, Schmidt-Thieme L. Factorization models for forecasting student performance. In Proc. the 3rd International Conference on Educational Data Mining, June 2010, pp.11–20.
[13] Wang X J, Berger J O, Burdick D S. Bayesian analysis of dynamic item response models in educational testing. The Annals of Applied Statistics, 2013, 7(1): 126–153. DOI: 10.1214/12-AOAS608.
[14] Anzanello M J, Fogliatto F S. Learning curve models and applications: Literature review and research directions. International Journal of Industrial Ergonomics, 2011, 41(5): 573–583. DOI: 10.1016/j.ergon.2011.05.001.
[15] Averell L, Heathcote A. The form of the forgetting curve and the fate of memories. Journal of Mathematical Psychology, 2011, 55(1): 25–35. DOI: 10.1016/j.jmp.2010.08.009.
[16] Ebbinghaus H. Memory: A contribution to experimental psychology. Annals of Neurosciences, 2013, 20(4): 155–156. DOI: 10.5214/ans.0972.7531.200408.
[17] Malliaris A G. Wiener process. In Time Series and Statistics, Eatwell J, Milgate M, Newman P (eds.), Springer, 1990, pp.316–318. DOI: 10.1007/978-1-349-20865-4_43.
[18] Liu B B, Dong W, Liu J X, Zhang Y T, Wang D Y. ProSy: API-based synthesis with probabilistic model. Journal of Computer Science and Technology, 2020, 35(6): 1234–1257. DOI: 10.1007/s11390-020-0520-4.
[19] Qiang Y T, Fu Y W, Yu X, Guo Y W, Zhou Z H, Sigal L. Learning to generate posters of scientific papers by probabilistic graphical models. Journal of Computer Science and Technology, 2019, 34(1): 155–169. DOI: 10.1007/s11390-019-1904-1.
[20] Zhang Q. Dynamic uncertain causality graph for knowledge representation and reasoning: Discrete dag cases. Journal of Computer Science and Technology, 2012, 27(1): 1–23. DOI: 10.1007/s11390-012-1202-7.
[21] Leighton J P, Gierl M J. Cognitive Diagnostic Assessment for Education: Theory and Applications. Cambridge University Press, 2007.
[22] Rasch G. Probabilistic Models for Some Intelligence and Attainment Tests. MESA Press, 1993.
[23] Khajah M, Wing R M, Lindsey R V, Mozer M C. Integrating latent-factor and knowledge-tracing models to predict individual differences in learning. In Proc. the 7th International Conference on Educational Data Mining, Jul. 2014, pp.99–106.
[24] Ekanadham C, Karklin Y. T-SKIRT: Online estimation of student proficiency in an adaptive learning system. arXiv: 1702.04282, 2017. https://arxiv.org/abs/1702.04282, Nov. 2023.
[25] Huang Z Y, Liu Q, Chen Y Y et al. Learning or forgetting? A dynamic approach for tracking the knowledge proficiency of students. ACM Trans. Information Systems, 2020, 38(2): 1–33. DOI: 10.1145/3379507.
[26] Cen H, Koedinger K, Junker B. Learning factors analysis—A general method for cognitive model evaluation and improvement. In Proc. the 8th International Conference on Intelligent Tutoring Systems, Jun. 2006, pp.164–175. DOI: 10.1007/11774303_17.
[27] Pavlik P I, Cen H, Koedinger K R. Performance factors analysis—A new alternative to knowledge tracing. In Proc. the 14th International Conference on Artificial Intelligence in Education, Jul. 2009. DOI: 10.3233/978-1-60750-028-5-531.
[28] Elo A E. The Rating of Chess Players, Past and Present. Arco Pub, 1978.
[29] Pelánek R. Application of time decay functions and the elo system in student modeling. In Proc. the 7th International Conference on Educational Data Mining, Jul. 2014, pp.21–27.
[30] Nižnan J, Pelánek R, Rihák J. Student models for prior knowledge estimation. In Proc. the 8th International Conference on Educational Data Mining, Jun. 2015, pp.109–116.
[31] Pelánek R, Papoušek J, Řihák J, Stanislav V, Nižnan J. Elo-based learner modeling for the adaptive practice of facts. User Modeling and User-Adapted Interaction, 2017, 27(1): 89–118. DOI: 10.1007/s11257-016-9185-7.
[32] Yudelson M. Individualization of Bayesian knowledge tracing through Elo-infusion. In Proc. the 22nd International Conference on Artificial Intelligence in Education, Jun. 2021, pp.412–416. DOI: 10.1007/978-3-030-78270-2_73.
[33] Kaya Y, Leite W L. Assessing change in latent skills across time with longitudinal cognitive diagnosis modeling: An evaluation of model performance. Educational and Psychological Measurement, 2017, 77(3): 369–388. DOI: 10.1177/0013164416659314.
[34] Zhan P D, Jiao H, Liao D D, Li F M. A longitudinal higher-order diagnostic classification model. Journal of Educational and Behavioral Statistics, 2019, 44(3): 251–281. DOI: 10.3102/1076998619827593.
[35] Pan Q Q, Qin L, Kingston N. Growth modeling in a diagnostic classification model (DCM) framework—A multivariate longitudinal diagnostic classification model. Frontiers in Psychology, 2020, 11: 1714. DOI: 10.3389/fpsyg.2020.01714.
[36] Zhan P D, He K R. A longitudinal diagnostic model with hierarchical learning trajectories. Educational Measurement: Issues and Practice, 2021, 40(3): 18–30. DOI: 10.1111/emip.12422.
[37] Zhan P D. Longitudinal learning diagnosis: Minireview and future research directions. Frontiers in Psychology, 2020, 11: 1185. DOI: 10.3389/fpsyg.2020.01185.
[38] Corbett A T, Anderson J R. Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction, 1994, 4(4): 253–278. DOI: 10.1007/BF01099821.
[39] González-Brenes J, Huang Y, Brusilovsky P. General features in knowledge tracing to model multiple subskills, temporal item response theory, and expert knowledge. In Proc. the 7th International Conference on Educational Data Mining, Jul. 2014, pp.84–91.
[40] Käser T, Klingler S, Schwing A G, Gross M. Dynamic Bayesian networks for student modeling. IEEE Trans. Learning Technologies, 2017, 10(4): 450–462. DOI: 10.1109/ TLT.2017.2689017.
[41] Pardos Z A, Heffernan N T. KT-IDEM: Introducing item difficulty to the knowledge tracing model. In Proc. the 19th International Conference on User Modeling, Adaptation, and Personalization, Jul. 2011, pp.243–254. DOI: 10.1007/978-3-642-22362-4_21.
[42] Thaker K, Huang Y, Brusilovsky P, He D Q. Dynamic knowledge modeling with heterogeneous activities for adaptive textbooks. In Proc. the 11th International Conference on Educational Data Mining, Jul. 2018, pp.592–595.
[43] Yudelson M V, Koedinger K R, Gordon G J. Individualized Bayesian knowledge tracing models. In Proc. the 16th International Conference on Artificial Intelligence in Education, Jul. 2013, pp.171–180. DOI: 10.1007/978-3-642- 39112-5_18.
[44] Liu Q, Huang Z Y, Yin Y, Chen E H, Xiong H, Su Y, Hu G P. EKT: Exercise-aware knowledge tracing for student performance prediction. IEEE Trans. Knowledge and Data Engineering, 2019, 33(1): 100–115. DOI: 10.1109/TKDE. 2019.2924374.
[45] Pardos Z A, Heffernan N T. Modeling individualization in a Bayesian networks implementation of knowledge tracing. In Proc. the 18th International conference on User Modeling, Adaptation, and Personalization, Jun. 2010, pp.255–266. DOI: 10.1007/978-3-642-13470-8_24.
[46] Pardos Z A, Heffernan N T. Using HMMs and bagged decision trees to leverage rich features of user and skill from an intelligent tutoring system dataset. Journal of Machine Learning Research W&CP, 201040. https://people.csail.mit.edu/zp/papers/pardos_JMLR_in_press.pdf, Nov. 2023.
[47] Piech C, Spencer J, Huang J, Ganguli S, Sahami M, Guibas L, Sohl-Dickstein J. Deep knowledge tracing. arXiv: 1506.05908, 2015. https://arxiv.org/abs/1506.05908, Nov. 2023.
[48] Zhang J N, Shi X J, King I, Yeung D Y. Dynamic key-value memory networks for knowledge tracing. In Proc. the 26th International Conference on World Wide Web, Apr. 2017, pp.765–774. DOI: 10.1145/3038912.3052580.
[49] Shen S H, Liu Q, Chen E H, Huang Z Y, Huang W, Yin Y, Su Y, Wang S J. Learning process-consistent knowledge tracing. In Proc. the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Aug. 2021, pp.1452–1460. DOI: 10.1145/3447548.3467237.
[50] Huang T, Yang H L, Li Z, Xie H K, Geng J, Zhang H. A dynamic knowledge diagnosis approach integrating cognitive features. IEEE Access, 2021, 9: 116814–116829. DOI: 10.1109/ACCESS.2021.3105830.
[51] Lu Y, Wang D L, Meng Q G, Chen P H. Towards interpretable deep learning models for knowledge tracing. In Proc. the 21st International Conference on Artificial Intelligence in Education, Jul. 2020, pp.185–190. DOI: 10.1007/ 978-3-030-52240-7_34.
[52] Pardos Z A, Bergner Y, Seaton D T, Pritchard D E. Adapting Bayesian knowledge tracing to a massive open online course in edX. In Proc. the 6th International Conference on Educational Data Mining, Jul. 2013, pp.137–144.
[53] Johnson M J. Scaling cognitive modeling to massive open environments. In Proc. the ICML Workshop on Machine Learning in Education, Jul. 2015. http://ml4ed.cc/attachments/XuY.pdf, Nov. 2023.
[54] Ruder S. An overview of gradient descent optimization algorithms. arXiv: 1609.04747, 2016. https://arxiv.org/abs/1609.04747, Nov. 2023.
[55] Bock R D, Aitkin M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika, 1981, 46(4): 443–459. DOI: 10.1007/ BF02293801.
[56] Segall D O. Multidimensional adaptive testing. Psychometrika, 1996, 61(2): 331–354. DOI: 10.1007/BF02294343.
[57] Feng M Y, Heffernan N, Koedinger K. Addressing the assessment challenge with an online system that tutors as it assesses. User Modeling and User-Adapted Interaction, 2009, 19(3): 243–266. DOI: 10.1007/s11257-009-9063-7.
[58] Chang H S, Hsu H J, Chen K T. Modeling exercise relationships in E-learning: A unified approach. In Proc. the 8th International Conference on Educational Data Mining, Jun. 2015, pp.532–535.
[59] Yang H Q, Cheung L P. Implicit heterogeneous features embedding in deep knowledge tracing. Cognitive Computation, 2018, 10(1): 3–14. DOI: 10.1007/s12559-017-9522-0.
[60] Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. In Proc. the 13th International Conference on Artificial Intelligence and Statistics, May 2010, pp.249–256.
[61] Liu Q, Wu R Z, Chen E H, Xu G D, Su Y, Chen Z G, Hu G P. Fuzzy cognitive diagnosis for modelling examinee performance. ACM Trans. Intelligent Systems and Technology, 2018, 9(4): 1–26. DOI: 10.1145/3168361.
[62] Jang E E. A *validity narrative: Effects of reading skills diagnosis on teaching and learning in the context of NG TOEFL [Ph. D. Thesis]. University of Illinois at Urbana-Champaign, Champagne, 2005.
[63] Gervet T, Koedinger K, Schneider J, Mitchell T. When is deep learning the best approach to knowledge tracing?. Journal of Educational Data Mining, 2020, 12(3): 31–54. DOI: 10.5281/zenodo.4143614.
[64] Hodges J L. The significance probability of the Smirnov two-sample test. Arkiv för Matematik, 1958, 3(5): 469–486. DOI: 10.1007/BF02589501.
[65] Wu R Z, Xu G D, Chen E H, Liu Q, Ng W. Knowledge or gaming?: Cognitive modelling based on multiple-attempt response. In Proc. the 26th International Conference on World Wide Web Companion, Apr. 2017, pp.321–329. DOI: 10.1145/3041021.3054156.
[66] Zhao X, Zhang J J, Li W S, Kahn K, Lu Y, Winters N. Learners’ non-cognitive skills and behavioral patterns of programming: A sequential analysis. In Proc. the 21st International Conference on Advanced Learning Technologies, Jul. 2021, pp.168–172. DOI: 10.1109/ICALT52272.2021.00058.
[67] Jiang L, Wang P Y, Cheng K, Liu K P, Yin M H, Jin B, Fu Y J. EduHawkes: A neural Hawkes process approach for online study behavior modeling. In Proc. the 2021 SIAM International Conference on Data Mining, Apr. 2021, pp.567–575. DOI: 10.1137/1.9781611976700.64.
[68] Zhang H, Huang T, Liu S Y, Yin H, Li J, Yang H L, Xia Y. A learning style classification approach based on deep belief network for large-scale online education. Journal of Cloud Computing, 2020, 9(1): 1–17. DOI: 10.1186/s13677-020-00165-y.
[69] Chen Y X, Li X O, Liu J C, Ying Z L. Recommendation system for adaptive learning. Applied Psychological Measurement, 2018, 42(1): 24–41. DOI: 10.1177/014662161769 7959.
[70] Dang F R, Tang J T, Pang K Y, Wang T, Li S S, Li X. Constructing an educational knowledge graph with concepts linked to Wikipedia. Journal of Computer Science and Technology, 2021, 36(5): 1200–1211. DOI: 10.1007/s11390-020-0328-2.
[71] Zhu J Z, Jia Y T, Xu J, Qiao J Z, Cheng X Q. Modeling the correlations of relations for knowledge graph embedding. Journal of Computer Science and Technology, 2018, 33(2): 323–334. DOI: 10.1007/s11390-018-1821-8.
[72] Nakagawa H, Iwasawa Y, Matsuo Y. Graph-based knowledge tracing: Modeling student proficiency using graph neural network. In Proc. the 2019 IEEE/WIC/ACM International Conference on Web Intelligence, Oct. 2019, pp.156–163. DOI: 10.1145/3350546.3352513.
[73] Chen C H, Liu G Z, Hwang G J. Interaction between gaming and multistage guiding strategies on students’ field trip mobile learning performance and motivation. British Journal of Educational Technology, 2016, 47(6): 1032–1050. DOI: 10.1111/bjet.12270.
[74] Hwang G J, Wang S Y. Single loop or double loop learning: English vocabulary learning performance and behavior of students in situated computer games with different guiding strategies. Computers & Education, 2016, 102: 188–201. DOI: 10.1016/j.compedu.2016.07.005.
[75] Chen S Y, Yeh C C. The effects of cognitive styles on the use of hints in academic English: A learning analytics approach. Educational Technology & Society, 2017, 20(2): 251–264.
[76] Muir M, Conati C. Understanding student attention to adaptive hints with eye-tracking. In Proc. the 19th International Conference on Advances in User Modeling, Jul. 2011, pp.148–160. DOI: 10.1007/978-3-642-28509-7_15.
[77] Wang Y T, Heffernan N T. The “assistance” model: Leveraging how many hints and attempts a student needs. In Proc. the 24th International Florida Artificial Intelligence Research Society Conference, May 2011.
-
期刊类型引用(1)
1. Kechen Qu, Kam Cheong Li, Billy T. M. Wong, et al. A Survey of Knowledge Graph Approaches and Applications in Education. Electronics, 2024, 13(13): 2537.  必应学术
必应学术
其他类型引用(0)
-
其他相关附件




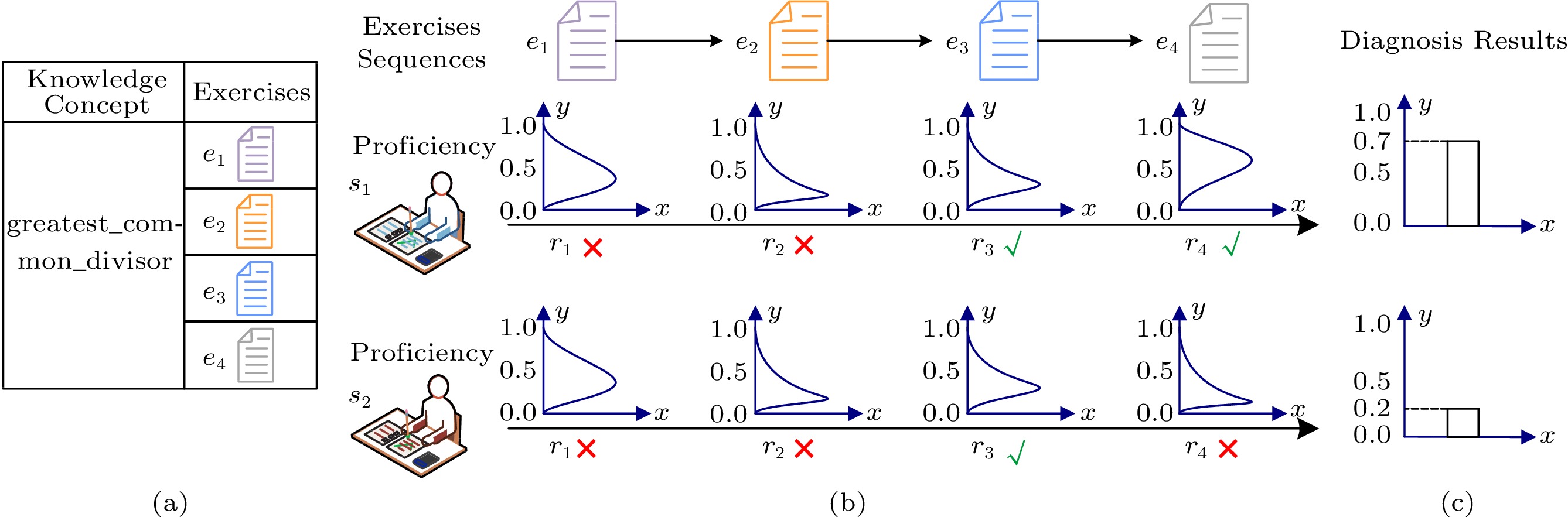
 下载:
下载: