1.   Introduction

1.1   Quantum Query Model

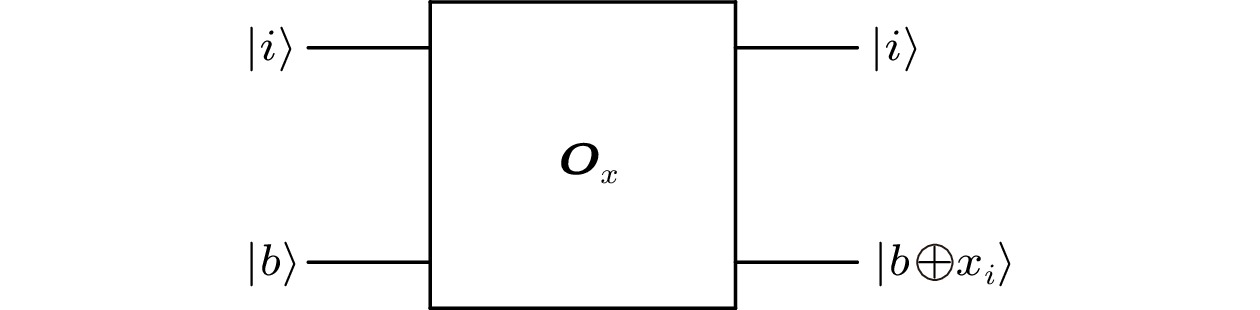
The decision tree model has been well studied in classical computing, and focuses on problems such as: given a Boolean function $f:\{0, 1\}^n\rightarrow \{0, 1\}$, how can we make as few queries as possible to the bits of x to output the value of $f(x)$? Quantum analog, called the Quantum Query model, has also attracted much attention in recent years^[1]. The implementation procedure of a quantum query model is a quantum query algorithm, which can be roughly described as follows: it starts with a fixed state $|\psi_0\rangle$ and then performs the sequence of operations ${\boldsymbol{U}}_0, {\boldsymbol{O}}_x, {\boldsymbol{U}}_1, \ldots, {\boldsymbol{O}}_x, {\boldsymbol{U}}_t$, where ${\boldsymbol{U}}_i$ is a unitary operator for any $i \in \{0, 1, \ldots, t\}$ that does not depend on the input x but the query oracle ${\boldsymbol{O}}_x$ does. This leads to the final state $|\psi_x\rangle=$ ${\boldsymbol{U}}_t{\boldsymbol{O}}_x{\boldsymbol{U}}_{t-1}\ldots {\boldsymbol{U}}_1{\boldsymbol{O}}_x{\boldsymbol{U}}_0|\psi_0\rangle$. The result is obtained by measuring the final state $|\psi_x\rangle$.

The quantum query model can be discussed in two main settings: the exact setting and the bounded-error setting. A quantum query algorithm is said to compute a function f exactly, if its output equals $f(x)$ with the probability of 1, for all inputs x. In this case, the algorithm is called an exact quantum algorithm. It is said to compute f with bounded errors, if its output equals $f(x)$ with a probability not less than 2/3, for all inputs x. Roughly speaking, the query complexity of a function f is the number of queries that an optimal (classical or quantum) algorithm should make on the worst input to compute f. The classical deterministic query complexity of f is denoted by $D(f)$, and the quantum query complexity in the exact setting is denoted by $Q_{\rm E}(f)$. In this paper, we focus on quantum query algorithms in the exact setting^[2-18], where quantum advantages are shown by comparing $Q_{\rm E}(f)$ and $D(f)$.

1.2   One-Query Quantum Algorithms

The Deutsch algorithm and the Deutsch-Jozsa algorithm are well known to be the first quantum algorithms and play a fundamental role in the history of quantum algorithms, as they exhibit the power of quantum computing for the first time and inspire the subsequent quantum algorithms. Different from many other quantum algorithms, the Deutsch algorithm and the Deutsch-Jozsa algorithm have the following characteristics: making only one query and returning the correct result with certainty. We call such a kind of quantum algorithms as exact one-query quantum algorithms. Now, a natural question is: what kind of problems can be solved by exact one-query quantum algorithms?

Recently, the characterization of one-query quantum algorithms (that can make only one query) has received some attention^{[2, 18–20]}. Aaronson et al.^[19] and Arunachalam et al.^[20] presented a complete characterization of the Boolean functions that can be computed by a one-query quantum algorithm in the bounded-error setting, but their results do not apply to the exact setting. Chen et al.^[2] considered the problem of what Boolean functions can be computed by exact one-query quantum algorithms, proving that a total Boolean function $f:\{0, 1\}^n \rightarrow \{0, 1\}$ can be computed by an exact one-query quantum algorithm if and only if $f(x)=x_{i_1}$ or $f(x)=x_{i_1} \oplus x_{i_2}$ (up to isomorphism). However, this does not hold for partial Boolean functions. Note that it has been known that any symmetric partial Boolean function f has $Q_{\rm E}(f) = 1$ if and only if f can be computed by the Deutsch-Jozsa algorithm^[18] (a Boolean function f is said to be symmetric, if $f(x)$ is determined by the number of 1 in x for each input x). But, it is unclear for the asymmetric partial functions. Actually, to the best of our knowledge, before this paper, no asymmetric partial function has been discovered to be computed by exact one-query quantum algorithms.

1.3   Our Contributions

All the above motivates us to consider the following questions. 1) What partial Boolean functions can be computed by exact one-query quantum algorithms? 2) Does there exist any asymmetric partial Boolean function that can be computed by an exact one-query quantum algorithm? For simplicity, throughout the paper “a function with $Q_{\rm E}(f) = 1$” always means that the function can be computed by an exact one-query quantum algorithm.

In this paper, we answer the first question by giving some necessary and sufficient conditions. Inspired by these conditions, we further answer the second question affirmatively, discovering some new representative functions with $Q_{\rm E}(f) = 1$. These functions generalize the already known functions and fill a gap in the discussion of asymmetric functions with $Q_{\rm E}(f) = 1$. Especially, while all the existing partial functions with $Q_{\rm E}(f) = 1$ are known to be symmetric and can be computed by the Deutsch-Jozsa algorithm, the functions discovered in this paper are generally asymmetric and new algorithms are required to compute these functions. Thus, this expands the class of functions that can be computed by exact one-query quantum algorithms.

The remainder of this paper is organized as follows. Related work is given in Section 2. The query model and the problem we consider are given in Section 3. Some necessary and sufficient conditions are presented in Section 4 for a Boolean function to be exactly computed by a one-query quantum algorithm. The construction and the discussion of new functions are shown in Section 5. Finally, a conclusion is made in Section 6.

2.   Related Work

For total Boolean functions, Beals et al.^[21] showed that exact quantum query algorithms can only achieve polynomial speed-up over classical counterparts. At the same time, Ambainis et al.^[4] proved that exact quantum algorithms have advantages for almost all Boolean functions. However, the biggest known gap between $Q_{\rm E}(f)$ and $D(f)$ had been only a factor of 2 for a long time, until a breakthrough result was obtained by Ambainis^[3], showing the first total Boolean function for which exact quantum algorithms have a superlinear advantage over classical deterministic algorithms. Furthermore, Ambainis et al.^[13] improved this result and presented a nearly quadratic separation.

For partial functions (promise problems), exponential separations between exact quantum and classical deterministic query complexity were obtained in several papers^{[5, 6, 11, 16]}. A typical example is the Deutsch-Jozsa algorithm^[5]. Additionally, some work showed an exponential separation between quantum and randomized query complexity in the bound-error setting, such as Simon's algorithm^[22] and Shor's algorithm^[23]. Recently, Childs and Wang^[24] proved that there is at most polynomial quantum speedup for (partial) graph property problems in the adjacency matrix model. On the contrary, in the adjacency list model for bounded-degree graphs, they exhibited a promise problem that shows an exponential separation between the randomized and quantum query complexities. Moreover, a series of work showed that for partial Boolean functions on N variables, the quantum query complexity could be exponentially smaller (or even less) than the randomized query complexity. Aaronson and Ambainis^[25] proposed a promise problem called Forrelation and showed that this problem can be solved by using one quantum query with bounded errors, yet any randomized algorithm needs $\widetilde{\Omega}(\sqrt{N})$ queries. They also showed that this separation is essentially optimal: any t-query quantum algorithm can be simulated by an $O(N^{1-1/2t})$-query randomized algorithm. Tal^[26] gave an $O(1)$ vs $N^{2/3-\epsilon}$ separation between the quantum and randomized query complexities of partial Boolean functions by a variant of the k-fold Forrelation problem. Furthermore, for any positive integer k, Bansal et al.^[27] and Sherstov et al.^[28] obtained a partial function on N bits that has bounded-error quantum query complexity at most $\lceil k/2 \rceil$ and randomized query complexity $\tilde{\Omega}(N^{1-1/k})$. This separation of bounded-error quantum versus randomized query complexity is the largest possible, by the results of Aaronson and Ambainis^[25].

Note that recently Xu and Qiu^[29] have independently carried out work on the similar topic as in this paper. Although we have not verified the proof of their main results, it is easy to see that our method and results are both different from their work. Compared with their work, we give different necessary and sufficient conditions to characterize the functions that can be computed by exact one-query quantum algorithms. Additionally, while another main object of [29] was to try to count the total number of partial Boolean functions with $Q_{\rm E}(f) = 1$, here we aim at explicitly constructing some representative asymmetric functions with $Q_{\rm E}(f) = 1$, with the hope to find some applications of these functions in future work. By the way, our proof is based on the general query oracle in Fig.1 defined by ${\boldsymbol{O}}_x|i, b\rangle = |i, b \oplus x_i\rangle$ for $i \in \{1,\ldots, n\}$, $b \in \{0, 1\}$.

Figure  1.  Quantum oracle

下载: 全尺寸图片 幻灯片

By restricting b to some special values, for $i \in \{1,\ldots, n\}$, we have

where $\left| - \right\rangle =(\left| 0 \right\rangle -\left| 1 \right\rangle )/{\sqrt{2}}$ and $\left| + \right\rangle = (\left| 0 \right\rangle +\left| 1 \right\rangle )/{\sqrt{2}}$. On the other hand, a simplified query oracle was considered in many papers, including [29], defined by

3.   Preliminaries

In this paper, we consider a Boolean function $f:\{0, 1\}^n \rightarrow \{0, 1\}$. It is called a total function, if it is defined for all $x\in\{0, 1\}^n$. It is called a partial function, if it is defined on a subset $D\subset \{0, 1\}^n$. A Boolean function f is said to be symmetric, if $f(x)$ is determined by the Hamming weight of x (i.e., the number of 1 in x), for each input x. In the following, we first give an introduction about the query models, including both classical and quantum cases, and then describe the problem to be discussed.

Given a Boolean function $f:\{0, 1\}^n \rightarrow \{0, 1\}$, we suppose $x=x_1x_2\ldots x_n \in \{0, 1\}^n$ is an input of f and we use $x_i$ to denote its i-th bit. The goal of a query algorithm is to compute $f(x)$, given queries to the bits of x.

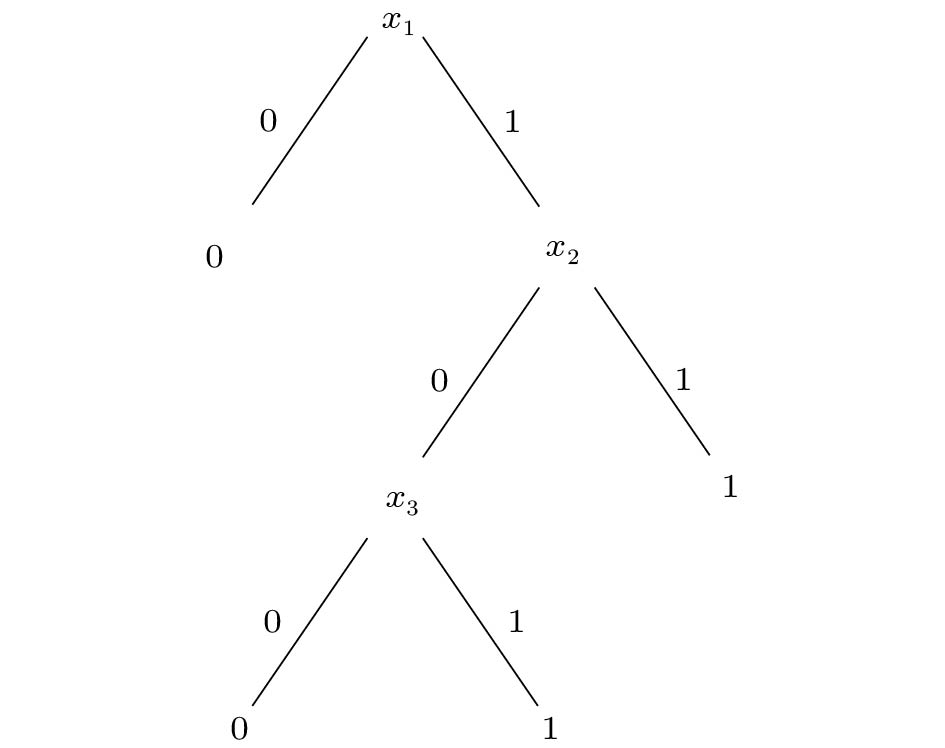
In the classical case, the process of querying x is implemented by using the black box (called query oracle) shown in Fig.2. We want to compute $f(x)$ by using the query oracles as few as possible. A classical deterministic algorithm for computing f can be described by a decision tree. For example, we want to use a classical deterministic algorithm to compute $f(x)=x_1 \land (x_2 \vee x_3)$. Then a decision tree T for that is depicted in Fig.3. Given an input x, the tree is evaluated as follows. It starts at the root. At each node, if it is a leaf, then its label is outputted as the result for $f(x)$; otherwise, it queries its label variable $x_i$. If $x_i$ = 0, then we recursively evaluate the left subtree. Otherwise, we recursively evaluate the right subtree. The query complexity of tree T denoted by $D(T)$ is its depth, and we have $D(T)=3$ in this example. Given f, there exist different decision trees to compute it, and the query complexity of f, denoted by $D(f)$, is defined as $D(f)=\min_TD(T).$

Figure  2.  Classical oracle.

下载: 全尺寸图片 幻灯片

Figure  3.  A decision tree T for computing $f(x)=x_1 \land (x_2 \vee x_3)$.

下载: 全尺寸图片 幻灯片

In the quantum case, the query oracle shown in Fig.1 is defined by ${\boldsymbol{O}}_x|i, b\rangle = |i, b \oplus x_i\rangle$ for $i \in\{1,\ldots, n\}$, $b \in \{0, 1\}$. Thus, we are able to query more than one bit each time due to quantum superposition.

A T-query quantum algorithm can be seen as a sequence of unitaries ${\boldsymbol{U}}_T{\boldsymbol{O}}_x{\boldsymbol{U}}_{T-1}{\boldsymbol{O}}_x\ldots{\boldsymbol{O}}_x{\boldsymbol{U}}_0$, where ${\boldsymbol{U}}_i$ is fixed unitary for any $i \in \{0, 1, \ldots, t\}$ and ${\boldsymbol{O}}_x$ depends on x. The process of computation is as follows:

1) start with an initial state $|\psi_{0}\rangle$;

2) perform the operators ${\boldsymbol{U}}_0, \;{\boldsymbol{O}}_x, \;{\boldsymbol{U}}_1, \;{\boldsymbol{O}}_x, \ldots, {\boldsymbol{U}}_T$ in sequence, and then obtain the state $|\psi_x\rangle= {\boldsymbol{U}}_T{\boldsymbol{O}}_x{\boldsymbol{U}}_{T-1}{\boldsymbol{O}}_x\ldots{\boldsymbol{U}}_0|\psi_{0}\rangle$;

3) measure $|\psi_x\rangle$ with a 0-1 positive operator-valued measurement^[30], and the result is regarded as the output of the algorithm.

In the above, we use $r(x)$ to denote the measurement result of $|{\boldsymbol{\psi}}_x\rangle$. Let $P[{\cal{A}}]$ denote the probability that event ${\cal{A}}$ occurs. If it satisfies:

where $\epsilon < {1}/{2}$, then the quantum query algorithm is said to compute $f(x)$ with bounded error $\epsilon$. If it satisfies:

then it is said to compute $f(x)$ exactly, and the algorithm is called an exact quantum algorithm. The exact quantum query complexity of f, denoted by $Q_{\rm E}(f)$, is the minimum number of queries that a quantum query algorithm needs to compute f. The gap between $D(f)$ and $Q_{\rm E}(f)$ is usually used to exhibit quantum advantages.

In this paper, we want to characterize the partial Boolean functions f with $Q_{\rm E}(f)=1$. In other words, we consider this problem: what partial Boolean function f can be computed by an exact one-query quantum algorithm?

4.   Necessary and Sufficient Conditions

First, we give some notations. For any n-bit string $x\in\{0, 1\}^n$, we always associate it with one bit $x_0 = 0$, and let $\left| x \right\rangle = \sum_{i=0}^n x_i|i\rangle$ be an $(n+1)$-dimension vector. Let us define $x'$ by $x'_i = (-1)^{x_i}$ for any i. For a non-negative diagonal matrix ${\boldsymbol{D}}$ of order $n+1$, let $|x_{{\boldsymbol{D}}}\rangle = \sqrt{{\boldsymbol{D}}}|x'\rangle$. If the trace of D $tr({\boldsymbol{D}}) = 1$, then $|x_{{\boldsymbol{D}}}\rangle$ is a unit vector. Let ${\boldsymbol{I}}_n$ be an $n\times n$ identity matrix and ${\boldsymbol{H}} = \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1& 1 \\ 1 & -1 \end{pmatrix}$.

Below, we give some necessary and sufficient conditions. Note that in the following proof the function f is not required to be total, and thus it holds for any Boolean function.

Theorem 1. The following statements are equivalent to each other.

1) $f:\{0, 1\}^n \rightarrow \{0, 1\}$ can be computed by an exact one-query quantum algorithm.

2) There exists a set of non-negative coefficients $\{c_i\}$ with $\sum_{i=0}^n c_i = 1$, such that $f(x) \neq f(y)$ implies $\sum_{i \in S}c_i = {1}/{2}$, where $S = \{i|x_i \neq y_i\}$.

3) There exists a non-negative diagonal matrix ${\boldsymbol{D}}$ with $tr({\boldsymbol{D}}) = 1$, such that $f(x) \neq f(y)$ implies $\langle x_{{\boldsymbol{D}}}|y_{{\boldsymbol{D}}} \rangle = 0$.

4) There exists a project operation ${\boldsymbol{P}}$ and a non-negative diagonal matrix ${\boldsymbol{D}}$ with $tr({\boldsymbol{D}}) = 1$, such that $f(x) = \langle x_{{\boldsymbol{D}}} |{\boldsymbol{P}}| x_{{\boldsymbol{D}}} \rangle$.

Proof. Statement 1 $\Rightarrow$ Statement 2. Suppose we have an exact one-query quantum algorithm. Let ${\boldsymbol{U}}_0 \left| \psi_0 \right\rangle =$ $\sum_{i, j, k}\alpha_{ijk}\left| i \right\rangle \left| j \right\rangle \left| k \right\rangle$, where $i \in \{1,\ldots, n\}$ and $j\in \{0, 1\}$. By Lemma 1 of [2], for any $x, y$ satisfying $f(x) \neq f(y)$, we have

Next we try to find a set of appropriate coefficients $\{c_i\}$. For $i \in \{1,\ldots, n\}$, let $c_i = \sum_k |\alpha_{i0k}-\alpha_{i1k}|^2/2$. Then $\sum_{i \in S} c_i = {1}/{2}$. Thus, we have

Let $c_0 = 1- \sum_{i=1}^n c_i$. Then $\sum_{i=0}^n c_i =1$. Thus, we find a set of feasible coefficients $\{c_i\}$.

Statement 2 $\Rightarrow$ Statement 3. We define diagonal matrix ${\boldsymbol{D}}$ by $D_{ii} = c_{i}$ for any i. If $f(x) \neq f(y)$, then

Statement 3 $\Rightarrow$ Statement 4. By statement 3, if $f(x) \neq f(y)$, then $\langle x_{{\boldsymbol{D}}}|y_{{\boldsymbol{D}}} \rangle = 0$. Let $X = \{|x_{{\boldsymbol{D}}}\rangle|f(x) = 1\}$, $Y = \{|y_{{\boldsymbol{D}}}\rangle| f(y) = 0 \}$. Then $X, Y \subset \mathbb{R}^{n+1}$ and $X \bot Y$. Let us select an orthonormal basis $\{|v_j\rangle\}$ of Span$\{X\}$. Let $g(x)=\sum_{j} \langle v_j|x_{{\boldsymbol{D}}}\rangle^2$. If $f(x)=1$, then $|x_{{\boldsymbol{D}}}\rangle \in$ Span$\{X\}$, and thus we have $g(x) = \| |x_{{\boldsymbol{D}}} \rangle \|^2= 1$. If $f(x)=0$, then for any j, $\langle v_j|x_{{\boldsymbol{D}}} \rangle = 0$, and thus $g(x)=0$. As a result, we have $f(x)=g(x)$. Let ${\boldsymbol{P}} = \sum_{j} |v_j \rangle \langle v_j|$. Then

Statement 4 $\Rightarrow$ Statement 1. By statement 4, we have $f(x) = \langle x_{{\boldsymbol{D}}}|{\boldsymbol{P}}|x_{{\boldsymbol{D}}} \rangle$. Suppose ${\boldsymbol{P}} = \sum_j \left| v_j \right\rangle \left\langle {v_j} \right|$ where $\left| v_j \right\rangle = \sum_{i=0}^n \alpha_{ij}\left| i \right\rangle$. Let $\left| {v'_j} \right\rangle = \sum_{i=1}^n \alpha_{ij} \left| i \right\rangle \left| 1 \right\rangle + \alpha_{0j} \left| 1 \right\rangle \left| 0 \right\rangle$ and ${\boldsymbol{P}}' =$ $\sum_j \left| {v'_j} \right\rangle \left\langle {v'_j} \right|$. Then we give Algorithm 1 to compute f. Strictly speaking, Algorithm 1 is not a concrete algorithm, since quantum circuits should be given explicitly for steps 1 and 3. However, it is sure that the algorithm uses only one quantum query and there exist quantum circuits to implement steps 1 and 3.

One can check that for any j, $\left\langle\psi_x \mid v_j^{\prime}\right\rangle = \langle x_{{\boldsymbol{D}}} \left| v_j \right\rangle$. Thus, the probability of output 1 is

and the probability of output 0 is $1-f(x)$. Thus, the algorithm always outputs correct results.□

In summary, statements 1–4 are equivalent, which may offer a deeper insight into what Boolean functions can be computed by an exact one-query quantum algorithm. Moreover, any one-query function f has the expression form $f(x) = \sum_j \langle v_j|x_{{\boldsymbol{D}}} \rangle^2 = \sum_j \langle v_j|\times \sqrt{{\boldsymbol{D}}}|x' \rangle^2$ by Theorem 1. Since $\left| x' \right\rangle = \sum_i x'_i\left| i \right\rangle$ and $x_i' = (-1)^{x_i} = 2x_i-1$, the degree of $\langle v_j|\sqrt{{\boldsymbol{D}}}|x' \rangle$ is 1. Thus, the expression of f in statement 4 satisfies that the degree of f $deg(f) \leqslant 2$, which meets the conclusion from the polynomial method^[1].

5.   New Representative Functions with One Quantum Query

5.1   New Functions

Here we find some new functions f with $Q_{\rm E}(f) = 1$ by Theorem 1. These examples help us understand the power of exact one-query algorithms better. To begin with, we list all the already known functions with $Q_{\rm E}(f) = 1$ (up to isomorphism)^{[5, 7, 18]}.

1) Deutsch-Jozsa function $f_1:\{0, 1\}^n \rightarrow \{0, 1\}$:

2) Symmetric function $f_2:\{0, 1\}^n \rightarrow \{0, 1\}$:

As stated in [18], the above functions can be computed by the Deutsch-Jozsa algorithm. Next, inspired by Theorem 1 we construct some new one-query functions f with $Q_{\rm E}(f) = 1$ that can be computed by Algorithm 1. We will show these functions satisfy statement 2 by giving the corresponding $\{c_i\}$ later.

3) For any set of non-negative coefficients $\{c_i\}$ satisfying $\sum_{i=0}^n c_i = 1$, there exists a quasi-symmetric function $f_3:\{0, 1\}^n \rightarrow \{0, 1\}$:

where $\hat{x} = \sum_{i=0}^n c_i x_i$.

4) Function $f_4: \{0, 1\}^4 \rightarrow \{0, 1\}$:

5) Function $f_5:\{0, 1\}^{4n} \rightarrow \{0, 1\}$: if x satisfies:

then $f(x) = 0$; if x appears in Fig.4, then $f(x) = 1$.

Figure  4.  Inputs whose function value is 1.

下载: 全尺寸图片 幻灯片

As mentioned earlier, a one-query function f has the expression: $f(x) = \sum_j \langle v_j|\sqrt{{\boldsymbol{D}}}|x' \rangle^2$. If a Boolean string set $\{w_j\}$ satisfies $|v_j\rangle = \sqrt{{\boldsymbol{D}}}|w_j\rangle$, then $f(x) = \sum_j \langle w_j|{\boldsymbol{D}}|x' \rangle^2$. Since ${D_{ii}} = c_i$ for any i, f depends on $\{c_i\}$ and $\{w_j\}$.

We give the corresponding $\{c_i\}$ and $\{w_j\}$ for the above functions as Table 1, which also means that ${{\boldsymbol{D}}}$ is given. Then we compute ${\boldsymbol{P}}'$ as follows. First, we compute $\left| v_j \right\rangle$ for any j. If $\left| v_j \right\rangle = \sum_{i=0}^n \alpha_{ij} \left| i \right\rangle$, let $\left| {v'_j} \right\rangle = \sum_{i=1}^n \alpha_{ij}\left| i \right\rangle \left| 1 \right\rangle +\alpha_{0j}\left| 1 \right\rangle \left| 0 \right\rangle$. Lastly, we have ${\boldsymbol{P}}' = \sum_j \left| {v'_j} \right\rangle \left\langle {v'_j} \right|$. After ${\boldsymbol{D}}$ and ${\boldsymbol{P}}'$ are given, we could use Algorithm 1 to compute these functions.

Table  1.  One-Query Functions with Their Corresponding $\{c_i\}$ and $\{w_j\}$

f	$\{c_i\}$	$\{w_j\}$
$f_1$	$c_{0} = 0,$ $c_{i} ={1}/{n}\ (\forall i>0)$	$w_1 = \underbrace{1\ldots1}_{n}$
$f_2$	$c_{0} = ({2c - n})/{2c},$ $c_{i} = {1}/({2c}) \ (\forall i > 0)$	$w_1 = \underbrace{1\ldots1}_{n}$
$f_3$	$\displaystyle\sum\limits_i c_i =1$	$w_1 = \underbrace{1\ldots1}_{n}$
$f_4$	$c_{i} = 0 \ (i \leqslant 2),$ $c_{i}=1/2\ (i> 2)$	$w_1 = 0011$
$f_5$	$c_{0} = 0,$ $c_{i} = {1}/({4n})\ (\forall i>0)$	${\left\{ \begin{array}{*{20}{l}} w_1 = \underbrace{1\ldots1}_{4n} \\ w_2 = \underbrace{1\ldots1}_{2n}\underbrace{0\ldots0}_{2n} \\ w_3 =\underbrace{1\ldots1}_{n}\underbrace{0\ldots0}_{n}\underbrace{1\ldots1}_{n}\underbrace{0\ldots0}_{n} \end{array} \right.}$

下载: 导出CSV 

| 显示表格

5.2   Characteristics of New Functions

Different from the already known one-query functions f with $Q_{\rm E}(f) = 1$, the new cases are generally asymmetric functions. In this way, our results fill a gap in the discussion of asymmetric functions that can be computed by exact one-query quantum algorithms. Next, we describe the characteristics of these functions.

1) Actually, $f_1$ and $f_2$ are both instances of $f_3$. If $c_0 = 0$ and $c_1 = \ldots =c_n$, then $f_3$ degenerates into $f_1$; if $c_0 \neq 0$ and $c_1 = \ldots =c_n$, then $f_3$ degenerates into $f_2$. Otherwise, $f_3$ is asymmetric. In this way, $f_3$ is a generalization of $f_1$ and $f_2$. It can not only include all the existing symmetric functions with $Q_{\rm E}(f) = 1$, but also represent a broad class of asymmetric functions with $Q_{\rm E}(f) = 1$.

2) Before $f_4$ being found, for any known n-bit one-query function f, there exists a function $f'$ isomorphic to f such that $f'^{-1}(1) \subseteq \{\underbrace{0\ldots0}_n, \underbrace{1\ldots1}_n\}$. However, $f_4$ is the first one-query function not satisfying this property. Moreover, it is also worth mentioning that $f_4$ and $f_1$ have the same domain when $n=4$.

3) $f_5$ is the first proper example represented as the sum of square form: $\sum_j \langle w_j|{\boldsymbol{D}}|x' \rangle^2$, whereas all previous examples can be represented as single square expressions: $\langle w_1|{\boldsymbol{D}}|x' \rangle^2$ (see Table 1). As a result, $f_5$ is more general and representative than previous cases in all functions with $Q_{\rm E}(f) = 1$.

6.   Conclusions

In this paper, we considered what partial Boolean functions can be computed by exact one-query quantum algorithms, obtaining several necessary and sufficient conditions for this problem. Furthermore, inspired by these conditions we discovered some new functions that can be computed by exact one-query quantum algorithms. Note that before this paper, all the existing functions with $Q_{\rm E}(f)=1$ are known to be symmetric and can be computed by the Deutsch-Jozsa algorithm. Contrarily, the functions constructed in this paper are generally asymmetric and we propose new algorithms to compute them. Thus, this expands the class of functions that can be computed by exact one-query quantum algorithms.

In the future, we hope to find some interesting applications of these functions. All these discussions are helpful for further consideration of the power of exact k-query quantum algorithms. Figuring out this problem is useful for understanding quantum query algorithms and inspiring us to find more problems with quantum advantages.