1.   Introduction

Frequent itemset mining (FIM), a branch of machine learning used for applications such as weblog mining and trend analysis, has recently attracted interest from many enterprises and researchers^[1-3]. FIM aims to identify the $k$ most frequent itemsets and their frequencies. The discovery of frequent itemsets can serve valuable economic and research purposes, e.g., mining association rules^[4], predicting user behavior^[5], and finding correlations^[6]. However, the direct publication of frequent itemsets incurs many risks, including leaking user preferences or individual transactions that include sensitive information. Therefore, to obtain statistical information while protecting user privacy is an important research direction.

This paper reports on a study of methods for frequent itemset mining (FIM) of transaction databases while guaranteeing privacy. Differential privacy (DP)^{[7, 8]} is an appealing and strict protection technology that can guarantee privacy even in the worst case. DP has become the de facto standard notion of privacy in research on private data analysis. A large domain and heterogeneous size are the two main characteristics in FIM^[9]. FIM with central DP is a mature research field^{[1, 10]}. In both interactive and non-interactive frameworks, centralized DP protocols for FIM seek to balance utility and privacy. However, DP requires a central trusted authority, which may leak private information. Protecting users' privacy requires the data aggregator to be trustworthy, but data aggregators lack credibility in most real-time applications. Consequently, as a decentralized technology, local differential privacy (LDP) has been considered for FIM; examples include LDPMiner^[11], PrivSet^[3], and set-value itemset mining (SVSM)^[9].

Motivation and Challenges. Our main motivation is to obtain more accurate statistical results than the state-of-the-art methods while guaranteeing the privacy. It is challenging to achieve these goals.

Unbiased and Low Variance. Most existing LDP approaches have an evident limitation in FIM when each user transaction has a set of items. LDPMiner^[11] dividing the privacy budget for two phases has a high variance of results. PrivSet^[9] perturbs items as a subset but with a large domain. SVSM^[3], a state-of-the-art protocol, should balance the bias and variance. Currently, it is still a challenging issue to obtain unbiased and low-variance frequencies for transactions with varied lengths. Thus, in this study, we develop an unbiased approach with low variance for FIM while protecting the privacy of items in each transaction.

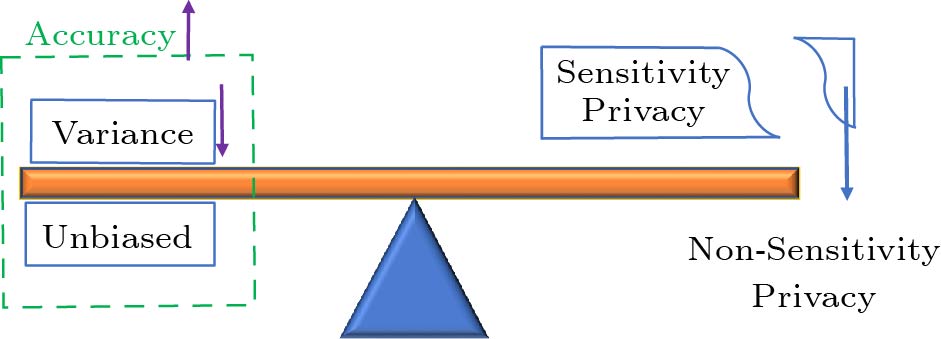
Contribution. Accuracy and privacy have always been considered in the academy and real world. In the FIM scenario in which a user has a set of items, the privacy (user-level) can be divided into sensitive privacy and non-sensitive privacy, and then we can sacrifice some non-sensitive privacy to obtain accurate results while guaranteeing sensitive privacy (Item-Level). It is considerable to sacrifice non-sensitive privacy of the user level to define the Item-Level LDP, which can improve the accuracy of the statistical results. Especially, if each user has only one item, the protection of the user level is equal to that of the Item-Level.

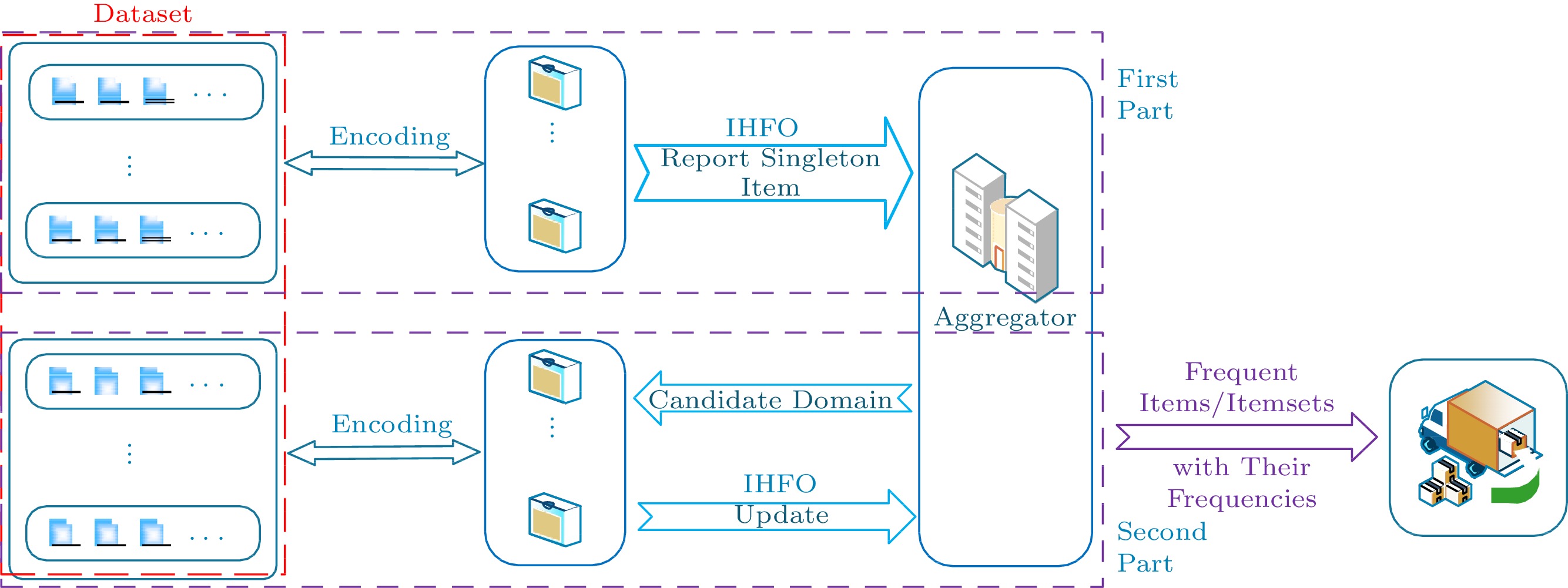
We split user-level privacy into two parts: the detail of items $y$ and the length $l_i$ of transaction of $T_i$. For the particular case in which $l_i$ is not sensitive and all the items should be considered as a whole, we define the Item-Level LDP for the privacy of items $y$ ($l_i$ = 1 is the traditional LDP case). We sacrifice non-sensitive privacy for more accurate results in Fig.1. This paper introduces an innovative Frequency Oracle (FO) approach, denoted as the Integrated-with-Hadamard-Transform-Based Frequency Oracle (IHFO), which leverages Hadamard encoding to achieve an unbiased and enhanced accuracy in frequency estimation while ensuring item-level local differential privacy (LDP). This approach builds upon the foundational work in privacy-preserving frequency oracles as delineated by Cormode et al.^[12]. Further advancing the state of the art, Wang et al.^[3] contributed additional FO methodologies, namely PSFO and PrivSet. PSFO is designed to strike a balance between minimizing variance and reducing bias, whereas PrivSet is tailored to identify frequent itemsets within a constrained error margin, particularly effective when the itemset size $|I|$ is small.

Figure  1.  Innovations: sacrificing non-sensitive privacy for more accurate results.

下载: 全尺寸图片 幻灯片

Based on IHFO, this paper presents an approach for FIM called United Itemset Mining (UISM). Like SVSM and LDPMiner, UISM divides the dataset into two parts: one to identify frequent singleton items and the other to update the frequent itemsets and estimate their frequencies. In both parts, UISM adopts IHFO to mine frequent items. We find that IHFO performs significantly well for the second part and PSFO performs better than the proposed IHFO when finding the rankings of singleton items. Therefore, we propose an optimized version called O-UISM, which combines the advantages of PSFO ($l$ = 1) and IHFO. O-UISM applies PSFO to search for frequent singleton items in the first part, and IHFO is used to obtain the estimated frequencies of frequent itemsets. Our experimental evaluation demonstrates the effectiveness of UISM and O-UISM. Table 1 presents an overview of FIM solutions.

Table  1.  Comparative Overview of FIM Solutions

FIM Method	Identification	Accuracy
SVSM <PSFO ($l$ = 1), PSFO ($l$ = adap$l$)>[3]	General	General
PrivSet<PSFO ($l$ = 1), PrivSet>	General	General
UISM<IHFO, IHFO>	General	Good
O-UISM<PSFO ($l$ = 1), IHFO>	Good	Good
Note: Identification refers to the accuracy rankings of the frequent items/itemsets, and accuracy denotes the accuracy frequencies of the frequent items/itemsets.

下载: 导出CSV 

| 显示表格

In summary, the main contributions of this paper are as follows.

● We define an Item-Level LDP and propose a Hadamard encoding based FO approach, namely IHFO, under the Item-Level LDP framework. The IHFO model encodes each itemset into a fixed length vector, which actually achieves the goal of unbiased FO estimating with lower variance and reducing the computation complexity.

● We provide an unbiased FIM approach, namely O-UISM. O-UISM combines PSFO and IHFO into a framework to achieve accuracy frequent itemsets together with their frequencies.

● We theoretically prove the unbiasedness and the lower variance of our protocols. Numerical experiments demonstrate that O-UISM can obtain more accurate frequent itemsets and frequencies with a lower squared error.

Roadmap. The remainder of this paper is organized as follows. We discuss related work and the preliminary of this work in Section 2. In Section 3, we definite the Item-Level LDP and propose our approaches to address the problems. Then, we provide a theoretical analysis of privacy and accuracy in Section 4. The experimental results are presented in Section 5. Finally, Section 6 concludes the paper.

2.   Related Work and Preliminary

In this section, we firstly introduce the related work, and then discuss the preliminary in this paper. Table 2 summarizes the notations used in this paper.

Table  2.  Notations

Notation	Definition
$\varepsilon$	Privacy budget
$I$	Domain of items
$\Psi$	Perturbation algorithm
$n$	Number of users
$v,x$	Singleton item
$y$	Itemset
$\boldsymbol b_i$	Encoding vector of user $i$
$T_i$	Transaction of user $i$
${\boldsymbol{H}}_r$	Hadamard matrices of order $2^r$ for every non-negative integer $r$
${\boldsymbol{H}}(v)$	Column vector that item $v$ maps to ${\boldsymbol{H}}_r$
SI	Set of frequent singleton items
CS	Set of candidate frequent itemsets
FIS	Set of frequent itemsets
w.p.	With probability

下载: 导出CSV 

| 显示表格

2.1   Related Work

Frequent itemset mining (FIM) is a well-studied problem in data mining. The FIM problem is identifying the frequent set of items that appear simultaneously in many users' transactions while guaranteeing privacy. Many protocols address this problem in the central DP^{[1, 13]} and LDP settings^{[3, 9, 11]}.

DP was first introduced by Dwork et al.^[8] and is currently the de facto standard of data privacy. Centralized DP has been the subject of numerous studies, both theoretical^[14] and practical^{[15, 16]}. Without a trusted aggregator, LDP can protect user privacy during data collection, addressing privacy leakage from the root^{[12, 17-19]} in many fields such as frequency oracle^{[20, 21]}, mean value^{[20, 22]}, FIM^{[3, 11]}, key-value pair estimation^{[23, 24]}, data monitoring^[25], federated learning^[26-28] and so on. Several variants of LDP and the corresponding mechanisms have been studied. Personalized LDP (PLDP)^[29] divides users into different groups according to different privacy budgets; by contrast, condensed LDP^[30], utility-optimized LDP^[31], and input discriminative LDP (IN-LDP)^[32] group the inputs based on defined rules to improve transmission accuracy. When the transactions have a set of items, user-level privacy needs to protect the transactions as a whole, whereas item-level privacy needs to protect the detailed items. The purpose of these definitions is to weaken the notion for the specialization of LDP.

Protecting user privacy during FIM is essential, and the use of DP in FIM has previously been investigated^{[1, 13]}. In both interactive^{[1, 13]} and non-interactive frameworks^[33], centralized DP protocols for FIM seek to balance utility and privacy. Because data aggregators are not credible in most real applications, protocols under local DP technologies are seldom applied to address this FIM problem^{[3, 11]}. Previously, Evfimievski et al.^[34] considered a more comfortable setting in which each transaction is assumed to have a fixed item length. However, this assumption cannot be applied to transactions of varied lengths. Qin et al. proposed LDPMiner^[11] to find frequent singletons while satisfying $\varepsilon$-LDP by adopting “padding and sampling”. One natural LDP algorithm is for each user to sample only one item and use known algorithms to send, which may miss the information of most items. PrivSet^[9] considers items as a whole, but the generated output range is too large. Then, the severe problem with PrivSet is that its calculation is prone to overflow when the parameters $I$ and $l$ are large. Furthermore, Wang et al.^[3] proposed the state-of-the-art SVSM, which can identify both singletons and itemsets. However, the frequency estimation of SVSM is biased. Thus, it would be promising and desirable for a new approach that guarantees unbiased estimation and obtains more accurate frequencies under the LDP framework.

2.2   Definition

2.2.1   Problem Definition

Let there be $n$ users and the domain of items $I$. Then, we obtain a set $\Gamma(I)$ consisting of all nonempty subsets of $I$, i.e., $\Gamma(I) = \{y|y\subseteq I, y \not\subset \emptyset \}$.

The aggregator aims to obtain the frequent items (or itemsets) of the dataset together with their frequencies. The frequent items (itemsets) can be defined by either determining the top-$k$ frequent items (itemsets) or finding items (itemsets) whose frequencies are above a certain threshold. The frequency of any item $x\in I$ is defined as the number of transactions that contain $x$, i.e., $f_x: = |\{i|x\in T_i\}|$. Similarly, the frequency of any itemset $y \in\Gamma(I)$ is defined as $f_y: = |\{i|y\subseteq T_i\}|$.

Definition 1 (Top-$k$ Frequent Itemset Mining). Given $n$ users with transaction $T_i$ $(1\leqslant i\leqslant n)$ from domain ${\cal{V}}$, a value $y \in {\cal{V}}$ is a top-$k$ frequent itemset if the frequency $f_y = |\{i|1\leqslant i\leqslant n, T_i\in {\cal{V}}\}|$ is ranked among the top $k$ frequencies of all possible itemsets.

2.2.2   Local Differential Privacy

LDP is a local model of DP for collecting user data without a credible aggregator^{[11, 19, 35, 36]}. An LDP algorithm $\Psi$ ensures that the probability of one value being sent to the aggregator approximates the probability of any other values being sent. The formal privacy requirement satisfies $\varepsilon$-LDP as follows.

Definition 2 ($\varepsilon$-Local Differential Privacy). Given an algorithm $\Psi$ with a domain $Dom(\Psi)$ and a range $Ran(\Psi)$, for items $t$ and $t'$ ($t,t' \in Dom(\Psi)$), the same output $s$ ($s \in Ran(\Psi)$) is transformed through algorithm $\Psi$ while satisfying the inequality (1), and we deem that $\Psi$ satisfies $\varepsilon$-LDP^[7].

We can adjust the privacy budget $\varepsilon$ to balance data availability and privacy. Moreover, LDP can provide a more robust privacy protection level than a centralized framework because each user reports only the perturbed data.

2.2.3   Frequency Oracle^[12]

The purpose of collection is to obtain frequency oracle (FO). FO is a core issue under the LDP framework, which has attracted a lot of theoretical and practical attention. FO approaches enable to estimate the frequency of any item/itemset in the domain. Wang et al.^[19] introduced an abstract framework of FO approaches, and showed that most previously proposed approaches can be placed within it.

2.2.4   Hadamard Transform Response (HTR)^{[17, 18, 37]}

The Hadamard (discrete Fourier) transform, known as the Walsh-Fourier transform, is described by an orthogonal-binary matrix ${\boldsymbol{H}}$ with dimensions of $2^r\times 2^r$ (where $r$ is any nonnegative integer). Its orthogonality has the natural advantage of classification in FO. The binarization is convenient for computer calculations and transmission, and the entry in $[row, col]$ is

where $row\in[0,2^r-1],col\in[0,2^r-1]$ and $Count{\mathbb{1}}()$ counts the number of $1$ in a binary integer. Moreover, the fast generation of the Hadamard matrix designed by the well-known Sylvester construction is as follows.

where $\boldsymbol H_0 = (1)$ and $r \geqslant 0$.

2.3   Competitors

Existing FO algorithms, such as OLH (optimized local hashing) and HTR, obtain their statistics in situations where each user transaction has only one item. Qin et al.^[11] and Wang et al.^[3] balanced the variance and bias to address the extension to each user transaction $T_i$ ($i = 1,2,\ldots,n$) having a set of items $v _i = \{x|x\in T_i, x\in I\}$. However, SVSM works less efficiently under such conditions when the lengths of transactions vary. In this case, it is challenging to develop an approach that guarantees an unbiased and low-variance frequency estimation.

PSFO^[3]. The PSFO approach addresses the scenario in which each transaction has a set of items derived from “padding and sampling” and then applies optimized local hashing (OLH) to report the items. Finally, the frequency estimation is multiplied by the padding parameter $l$ to obtain an accurate result. The variance in PSFO is

The choice of $l$ is important when using PSFO. If $l$ is small, there is less variance but more bias; if $l$ is large, there is less bias but more variance.

PrivSet^[9]. In the mechanism, the set-valued data is sanitized holistically by randomly outputting a fixed-size subset of items $\hat{s}$. First, each user uses “padding” to generate $T_i'$ according to $l$, where $T_i'$ contains the original $T_i$ and ($l-|T_i|$) padding items. Second, each user generates a perturbed subset $\hat{s}$ from a discrete probability distribution of all candidate itemsets whose weights follow (2):

where $u(T_i',\hat{s}) = [T_i'\cap \hat{s} \neq \emptyset]$. If $T_i'\cap \hat{s} = \emptyset$ then $u(T_i',\hat{s}) = 1$ (otherwise 0). Therefore, the probability of each $\hat{s}$ is ${Weight(\hat{s})}/{\sum\nolimits_{s\in S}Weight(s)}$.

SVSM. By using PSFO repeatedly, SVSM is the state-of-the-art approach for solving FIM in the LDP setting, where each user transaction has a set of items. SVSM divides a database ${{D}}$ into three parts ${{D}}_{\rm{A}}$, ${{D}}_{\rm{B}}$ and ${{D}}_{\rm{C}}$, where ${{D}}_{\rm{A}}$, ${{D}}_{\rm{B}}$ and ${{D}}_{\rm{C}}$ are applied to obtain frequent single items, adaptive $l$, and a final frequent itemset, respectively. When we identify a frequent set of terms in ${{D}}_{\rm{A}}$, a small $l = 1$ does not affect the ranking of items because the bias tends to be in the same direction for all items. However, when we need to obtain the frequencies of itemsets in ${{D}}_{\rm{C}}$, an adaptive $l$ from ${{D}}_{\rm{B}}$ is used to balance the bias and variance, which could cause bias and inaccurate results. All steps adopt PSFO, which is based on the OLH algorithm. In the first part, SVSM finds the set of frequent singleton items $SI$ to construct the candidate itemset $CI$ at the expense of frequency accuracy by setting $l = 1$. Then, the adaptive $l$ is required for accurate frequency acquisition, which is the task of the second part. Finally, by combining $CI$ and the adaptive $l$, the frequent itemsets and their respective frequencies are updated in the third part. Note that $CI$ consists of the top-$k$ frequent itemsets obtained through (3) based on $SI$,

where $y$ denotes any itemset and the factor of 0.9 is fixed in [3], which can lower the normalized estimates for the most frequent item.

3.   Method for FIM

Our work is on frequency estimation and means estimation for FIM with LDP, which is related to these existing methods^{[3, 9, 11]}, as we must handle a variable transaction length. Moreover, when a user has a set of items, it can be treated as a small database, which can view the problem from the user level and item level. Inspired by the analysis of the user level and item level^[38] in DP, although the above LDP algorithms are user-level, they are different. For example, these studies^{[3, 11, 34]} randomly select an item and use the item-level perturbation algorithm, and PrivSet^[9] perturbs a subset of items as a whole. This raises a problem that if each local user protects the privacy for each item in his/her own small database, the privacy for all items as a whole is protected. Therefore, this paper defines the Item-Level LDP and proposes two methods to address the above problems.

In this section, we define the Item-Level LDP and propose a baseline approach called IHFO to handle the fact that each transaction has a set of items. IHFO protects all items in each transaction while guaranteeing an unbiased and low-variance frequency estimation. For frequent item/itemset mining (item mining and itemset mining are similar; thus, we discuss them together), we propose a general version, namely UISM. And then, we suggest an optimal version called O-UISM, which combines PSFO ($l$ = 1) and IHFO into a framework to achieve accuracy frequent itemsets together with their frequencies. The protocol structure of UISM is given in Fig.2. In the framework, the dataset is divided in two parts. The first part is applied to obtain frequent singleton items, and the second part is applied to obtain frequent itemsets with their frequencies. Both parts need to encode the pre-processed items, and then report to the aggregator with LDP perturbation. The aggregator sends the decoded results of the first part to the second part, and decodes the collection of the second part to output the frequent itemset with their frequencies. If the protocol of the first part is replaced by PSFO ($l$ = 1), this framework is called O-UISM.

Figure  2.  Illustration of UISM.

下载: 全尺寸图片 幻灯片

3.1   Definition of Item-Level

In the LDP case, the definition is too strict to guarantee the accuracy of the dataset for the user level. Because user $i$ has multiple items $T_i$, one natural user level algorithm is for each user to sample only one item and use known algorithms to send, which may miss the information of most items. We consider that if $|T_i|<<|I|$ and $|T_i|>0$, the length of transaction $|T_i|$ is not sensitive for the user, and each item in the transaction is sensitive. Then, the items in the transaction need to be protected more carefully than the number of items. Inspired from the view of specialization of LDP^[29-32], we develop a loose definition of LDP, namely Item-Level $\varepsilon$-LDP 3, to design protocols that offer desirable statistical utility while preserving privacy.

Definition 3 (Item-Level $\varepsilon$-Local Differential Privacy). Given an algorithm $\Psi$ with a domain $Dom(\Psi)$ and a range $Ran(\Psi)$, any two users $i$ and $i'$ with transactions $T_i$ and $T_i'$ report <$|T_i|,\ \Psi(T_i)$> and <$|T_i'|,\ \Psi(T_i')$> respectively. If the same output $S$ ($S \in Ran(\Psi)$) is transformed through algorithm $\Psi$ while satisfying the inequality (4), we assume that the algorithm $\Psi$ satisfies $\varepsilon$-LDP:

Note that inevitably, some private data is revealed. For example, in the extreme case, $|T_i| = 0$ or $|T_i| = |I|$, implying that the user has no item or possesses all items in the item domain, respectively. However, $|T_i|<<|I|$ and $|T_i|>0$ are the majority of cases in practice. To ensure broad applicability, a marginally relaxed interpretation of local differential privacy is necessitated. This research endeavors to safeguard the privacy of the user's transaction set $|T_i|$, albeit not to the extent of the stringent $\varepsilon$-LDP threshold. Consequently, the privacy assurance of our proposed protocols is positioned above the Item-Level $\varepsilon$-LDP.

3.2   IHFO: Based Approach

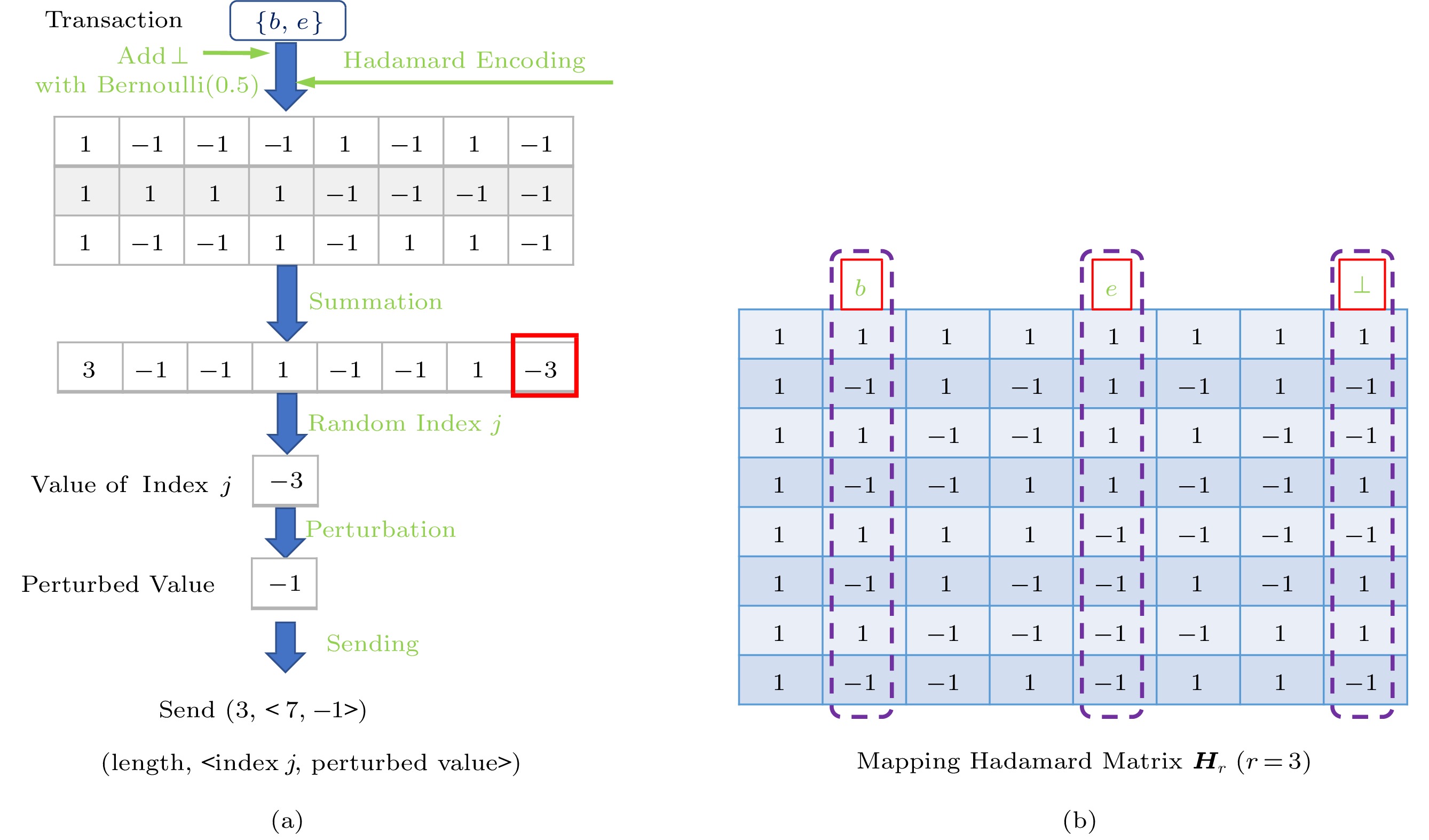
Traditional approaches^{[3, 9]} use “padding and sampling” to protect privacy while satisfying $\varepsilon$-LDP, which discards most of the information in the transaction. IHFO uses the Hadamard transform to encode all items in each transaction. The vectors in the Hadamard transform matrix are orthogonal to each other and binarized; therefore, regardless of the number of items in the user transaction, they can be encoded into a vector with a fixed length. Next, adding LDP perturbations to this vector preserves the items in each transaction, thereby allowing datasets with varied transaction lengths to be handled. Finally, the aggregator collects all vectors and estimates the frequencies of items. The entire process of IHFO is divided into three phases: encoding, perturbation, and decoding. The detailed process of IHFO is shown in Algorithm 1 and the illustration of encoding and perturbation in IHFO is in Fig.3. For example, user $i$ has a transaction with items $\{b, e\}$. After adding an extra item $\perp$, this transaction has three items (the length is equal to 3). In the first phase, three items are encoded to three column vectors from the Hadamard matrix (in order to facilitate understanding, we paint them as row vectors). Then, the user sums these vectors and selects one index $k_i = 7$ with its value $b_i[7] = -3$. After perturbing the value $b_i[7]$ by (5) to $z_i[7] = -1$ ($z_i[k_i]\in \{1,-1\}$), the perturbed tuple (3, <7, –1>) should be sent to the aggregator where $< k_i, z_i[k_i] >$ satisfies LDP and ($|\{b,c\}\cup \{\perp\}|, < k_i,z_i[k_i] >$) satisfies the Item-Level LDP.

Figure  3.  Illustration of encoding and perturbation in IHFO. (a) Process of IHFO. (b) Mapping Hadamard matrix.

下载: 全尺寸图片 幻灯片

Encoding. First, each transaction is added an extra item $\perp$ with a Bernoulli(0.5) distribution separately (if $l_i = 0$, we also add $\perp$). Then, we encode all items in the user transaction with a Hadamard matrix ${\boldsymbol{H}}_r$, where $r = \lceil\log_2{|I\cup \{\perp\}|}$$\rceil$. We assume that each item $v,v\in I\cup \{\perp\}$ is uniquely mapped to a column vector ${\boldsymbol{H}}(v)$ of a Hadamard matrix ${\boldsymbol{H}}$ (unless otherwise stated, all symbols ${\boldsymbol{H}}$ below represent ${\boldsymbol{H}}_r$). Then, each user $i$ can obtain the encoding vector $\boldsymbol b_i = \sum_{v\in T_i} {\boldsymbol{H}}(v)$, and the number of items $l_i = |T_i|$ in the transaction ($T_i$ comprises old transactions and random $\perp$). The special item $\perp$ is a perturbation that renders it impossible for an attacker to confirm how many items are in each user transaction.

Perturbation. User $i$ randomly selects the $k_i$-th entry of $\boldsymbol b_i$ and perturbs $b_i[k_i]$ independently with the following distribution:

Finally, user $i$ releases $z_i[k_i]$ and $l_i$ to the aggregator. As $k_i$ is the position of vector $\boldsymbol b_i$, $z_i[k_i]$ requires $r+1$ bits for communication, where $r$ bits represent the position of $k_i$ (i.e., any position $j_i\ne k_i$, $z[j_i] = 0$).

Decoding. The aggregator collects all the noise information to obtain a vector of summation $\boldsymbol z = \sum_i^n z_i\ l_i$. Then, the unbiased frequency estimation of item $v$ is given by

Each user sends $(z_i[k_i],l_i)$ to the aggregator, where $z_i[k_i]$ represents the value of items in the transaction under the LDP perturbation and $l_i$ represents the length of the transaction. We consider it feasible to sacrifice some privacy of the length to obtain more accurate FO (more specifically, the user reports the true length $l_i$ with the probability of $50\%$ and reports the true length plus 1 $(l_i+1)$ with the probability of $50\%$). Differently expressed, only $z_i[k_i]$ in $(z_i[k_i],l_i)$ satisfies LDP and protects the privacy of the items. We also analyze the privacy protection in Section 4.

3.3   UISM: A General Version

If an itemset is frequent, then each item in the itemset is also clearly frequent. However, given a particular dataset, we cannot intuitively determine which itemsets are frequent. Frequent itemsets cannot be obtained directly because even if the domain of items is not large (e.g., $|I| = 1\;000$), the number of possible itemsets will be $|\Gamma(I)| = 2^{1\;000}$, which is disastrous for the aggregator. Moreover, because most itemsets' frequencies are low, the aggregator must first reduce the domain of candidate itemsets. When the set of candidate itemsets is small, users will send more available data after the perturbation, which increases the accuracy of the frequency estimation. Thus, UISM divides users into two groups: $FS$, which is applied to generate candidate itemsets by finding the frequent singleton items, and $FF$, which is applied to update the frequent itemsets and estimate their frequencies, i.e.,

Step 1: Find Frequent Singleton Items. Candidate itemsets are generated based on frequent singleton items. The larger the number of accurate singleton items, the more accurate the candidate itemsets, which is beneficial for obtaining frequent itemsets together with their frequencies in step 3. Thus, the frequent singleton itemset $SI$ with noisy frequencies $f^{SI}$ is obtained by $\Psi_{\rm{IHFO}}$ using

Step 2: Generate Candidate Itemsets^[3]. Because each item in a frequent itemset is frequent, we construct a set according to the following formula:

where $t$ is chosen such that $|CS| = 2k$. To reduce the calculation cost, $t$ should take at least $p_x$ under the $k$-th singleton item $x$.

Step 3: Update Frequent Itemsets and Estimate Their Frequencies. After the domain $CS$ is defined, each user in the second part of the dataset constructs their transaction (i.e., $T_i' = \{x|x\subseteq T_i, x \subseteq CS\}$). The aggregator receives information from users via the IHFO algorithm. After the correction, the aggregator updates the top-$k$ frequent itemsets and their respective frequencies as the released result.

The UISM protocol addresses the challenge of set-valued inputs by using the Hadamard transform response FO approach to report after encoding all items in each transaction. This protocol can guarantee the accuracy of the frequency estimation.

3.4   O-UISM: An Optimal Version

We find that if the top-rank frequent singleton items are more precise, the frequent itemsets with their frequencies are more accurately obtained through UISM. Moreover, the ranks of singleton items are more important than the frequencies in step 1. As described previously, in SVSM, PSFO ($l$ = 1) sacrifices the frequency accuracy to obtain a good rank. Thus, we adapt $\Psi_{{\rm PSFO}\enspace(l = 1)}$ to find frequent singleton itemset $SI$, as shown in (6).

By combining the advantages of PSFO (l = 1) and IHFO, we propose O-UISM for FIM. Thus, O-UISM can more accurately obtain frequent itemsets and frequencies with a lower squared error. Note that we can apply any FO algorithm to replace PSFO (l = 1).

4.   Analysis

4.1   Privacy Guarantee

We protect privacy from three aspects.

1) Hadamard Encoding and Sampling. Hadamard encoding and sampling provide some privacy protection because even if the privacy budget is large, the aggregator can obtain minimal information from each sending value.

2) Symbol $\perp$. We add $\perp$ to provide some protection of $|T_i|$. The aggregator needs to guess the length of the transaction from $|T_i|$ and $|T_i|-1$.

3) $\varepsilon$-LDP. We protect the sending value under the most rigorous standard of data privacy.

Lemma 1.Special item $\perp$ protects the items of transaction.

Proof. A special item $\perp$ represents an extra item added to each transaction from a Bernoulli(0.5) distribution. The aggregator cannot then distinguish the accuracy length of the transaction between $|T_i|$ and $|T_i|-1$ obtained from user $i$. Item $\perp$, as a dummy item, is applied to defend the attraction. In particular, if $|T_i| = 0$, we must add symbol $\perp$ in this transaction.□

Lemma 2.The perturbation value $z_i$ satisfies $\varepsilon$-LDP.

Proof. We assume that two users have transactions $T_1$ and $T_2$ with lengths $l_1$ and $l_2$, respectively. Let $k$ be any position and $RC$ be the ratio of two conditional probabilities with $T_1$ and $T_2$ transactions. The sensitivity is maximized when $b_1$ is maximum and $b_2$ is minimum (i.e., $b_1[k] = l_1$, and $b_2[k] = -l_2$):

Theorem 1. IHFO provides higher protection than Item-Level $\varepsilon$-LDP but also lower protection than $\varepsilon$-LDP.

Proof. If a mechanism satisfies the LDP, it provides privacy protection at a high level. Lemma 2 proves that the value $z_i$ in IHFO satisfies $\varepsilon$-LDP. If we send the actual length of the transaction, IHFO satisfies Item-Level $\varepsilon$-LDP. However, we also protect the length of transaction in Lemma 1. Thus, IHFO provides higher protection than Item-Level $\varepsilon$-LDP but also lower protection than rigorous $\varepsilon$-LDP.□

4.2   Accuracy Analysis

Here, we analyze the accuracy improvement of the proposed framework by evaluating unbiased estimation in Theorem 2 and the error bound in Lemma 3. Then, we compare the variance between IHFO and PSFO. Finally, we analyze the communication cost and computational complexity of PSFO and IHFO.

Theorem 2.The estimated frequency $f_v$ is unbiased.

Proof. We assume that $\hat{z}$ is the real summation of the encoding bits, where $\hat{z} = \sum_i^n \boldsymbol b_i$. Then, the real frequency of any item $v$ is given by

Considering that each user $i$ randomly selects the $k$-th entry of $\boldsymbol b_i$ with the probability of $1/{2^r}$, the mean value of the $k$-th entry in $z$ can thus be expressed as

Hence, the mean frequency of item $v$ is as follows.

Theorem 3 (Upper Bound). Let $d = 2^r$. As described previously, $\hat{f_v} =(1/d){\boldsymbol{H}}(v)^{\rm{T}}\sum_{i = 1}^n\boldsymbol b_i$ and $f_v = (({{\rm{e}}^{\varepsilon}+1})/({{\rm{e}}^{\varepsilon}-1})) {\boldsymbol{H}}(v)^{\rm{T}}\cdot\sum_{i = 1}^nz_i l_i$. With the probability of at least $1-\beta$,

Proof. In the IHFO algorithm, $f_v$ is the unbiased counterpart of $\hat{f_v}$ obtained by Theorem 2. Let $\hat{t_i} =$ $(1/d)({\boldsymbol{H}}(v)^{\rm{T}} \cdot b_i)$ and $t_i = (({{\rm{e}}^{\varepsilon} + 1})/({{\rm{e}}^{\varepsilon} - 1}))({\boldsymbol{H}}(v)^{\rm{T}} \cdot z_i l_i)$. Thus, $|f_v-\hat{f_v}|\leqslant (({{\rm{e}}^\varepsilon+1})/({{\rm{e}}^\varepsilon-1}))\ l_i +1$. Then, by Bernstein's inequality,

For each position $k$ in $z_i$, if $k\ne k_i$, then $z_i[k] = 0$; the other case satisfies (5).

Thus,

Substituting (8) and $({{\rm{e}}^\varepsilon+1})/({{\rm{e}}^\varepsilon-1})\times l_i +1 =$ $O\left({l_i}/\varepsilon\right)$ into inequality (7), we obtain

By the union bound, there exists

Variance. The variance in the frequency of item $v$ in IHFO is denoted as

Theorem 4. The mean of $Var_{\rm{IHFO}}$ is lower than that of $Var_{\rm{PSFO}}$ when $\varepsilon<\log{\sqrt{1440}}\approx 3.6$ and

for a distribution ${\cal{X}}$ with mean $\mu$ and variance $\sigma^2$.

Proof. We should compare the variance of

$Var_{\rm{IHFO}} = ({({\rm{e}}^{\varepsilon}+1)^2})/{({\rm{e}}^{\varepsilon}-1)^2})\sum_{i = 1}^m p_i\times l_i^2$

and

$Var_{\rm{PSFO}}= {4 {\rm{e}}^\varepsilon}/({({\rm{e}}^{\varepsilon}-1)^2}) l^2$

where $l: inf\sum_{i = 1}^l p_i\geqslant 0.9$ (we omit the same $n$ for the sake of calculation). According to Chebyshev's inequality (9) and $1- {\sigma^2}/{\omega^2} = 0.9$ for a distribution with mean $\mu$ and $\sigma^2$,

We obtain $\omega \geqslant \sqrt{10}\sigma$. Then $l \geqslant \omega+\mu$ in PSFO.

From (10), if $\varepsilon<\log{\sqrt{1440}\approx 3.6}$ and

the variance of IHFO is lower than that of PSFO.□

We use the mean of variance to compare, which may lose efficacy. Owing to padding and sampling, PSFO must transmit a value unrelated to the transaction, contributing little to calculating the item frequency. However, each value transferred through IHFO contributes part of the information on all items in this transaction. For example, in the practical setting, the privacy budget $\varepsilon\in[1,2]$, and the dataset confirms Poisson distribution ${\cal{X}}(\lambda)$. Thus, we set $\varepsilon$ = $\ln 3$ for the general cases. We can obtain that the variance of IHFO is better when $\lambda\leqslant$31, which can be applied in most real FIM cases.

4.3   Complexity Analysis

The Hadamard transform approach has been cited in many LDP papers^{[17, 18, 37]} and is variously described, though always with the same core concept. Every user value is mapped to a column in the Hadamard matrix and then sends a random entry to the aggregator after combining with the LDP noise. Advantages exist on both the user side and the aggregator side: at the user side, the HTR achieves a good tradeoff between data availability and communication cost since each user transmits only $r+1$ bits (if a random number is generated by the aggregator, $1$ bit is sufficient). The computational complexity of the aggregator in reconstructing the FO is $O(n+r\times 2^r)$, versus $O(2^r\times n)$ for the OLH, since the aggregator needs to sum up only the collected information and then takes the linear product of the matrices.

The communication costs of IHFO and PSFO are related to different parameters, but the aggregator's computational complexity is lower than that of the PSFO approach in Table 3. For PSFO, each user should transform $O(\log_2 \sqrt n+\log_2 g) =O(\max\{\log \sqrt n,$ $\log g\})$ bits using the OLH algorithm. Then, the computational complexity of the aggregator is $\varOmega (n^{\tfrac 32})$($\sqrt n$ hash functions). For IHFO, each user should send three parameters: the location of the sampling, positive and negative values, and transaction length. Thus, the communication cost is $O(\lceil \log_2{|I|} \rceil+\log_2 l_i+ 1 ) = O(\log{|I|})$. After summing all vectors, the aggregator needs only to calculate the inner matrix product once to obtain the frequency estimation; thus, the computational complexity is $\varOmega(n)$.

Table  3.  Communication and Computation Cost

FO Method	Communication (Each User)	Computation (Aggregator)
PSFO	$O(\max\{\log \sqrt n, \log g\})$	$\varOmega (n^{3/2})$
IHFO	$O(\log{|I|})$	$\varOmega(n)$
Note: Communication cost denotes the bits in the collection that each user should send to the aggregator; computation cost denotes the computation complexity of the aggregator in correction.

下载: 导出CSV 

| 显示表格

As O-UISM applies IHFO to estimate frequent itemsets with their frequencies, it also achieves the goal of unbiased estimating with lower variance and reducing the computation complexity.

5.   Experimental Evaluation

In this section, we report experiments on real datasets to validate our analysis with different protocols.

5.1   Experimental Setup

Environment. All algorithms were implemented in Python 3.7.3, and all experiments were conducted on an Intel Core^TM i7-6700 3.40 GHz PC with 16 GB RAM. We report the average results over 10 runs.

Datasets. We ran experiments on the following datasets.

● Online ¹. This dataset contains the merchant transactions of 500000 users with 2603 categories.

● IBM ². This dataset was generated by the IBM Synthetic Data Generation Code for Associations and Sequential Patterns with 1.8 million transactions generated over 1000 categories. The average transaction length is 5.

Metrics. This study aims to find frequent itemsets together with their frequencies, which requires different metrics to evaluate their utilities. We adopt the normalized cumulative rank (NCR)^[3], squared error (SE) and Kullback-Leibler divergence (KLD) to assess the frequent itemsets and frequencies, respectively. NCR is used to measure the accuracy ranks of the frequent items/itemsets, and SE and KLD are used to measure the accuracy frequencies of the frequent items.

1) Normalized Cumulative Rank (NCR). The quality function with the most $k$ values ranked is as follows: the highest ranked value has a score of $k$, the next one has a score of $k-1$, and so on. The $k$-th value has a score of 1, and all the other values have scores of 0. To normalize this into a value between 0 and 1, we divide the sum of scores by the maximum possible score (i.e., ${k(k+1)}/2$).

2) Squared Error (SE). We measure the estimation accuracy using the squared error. That is,

where $RS$ is the real set of frequent itemsets with frequencies $f^{RS}$. Note that we account only for heavy hitters that are successfully identified by the protocol (i.e., $y\in FIS\cap RS$). Thus, lower variance means more accurate estimation.

3) Kullback-Leibler Divergence (KLD). Csisz$\acute{a}$rs f-divergence is used to measure whether a privacy mechanism is an information-theoretic quantity, and the distributional difference is defined in (11)^[39].

where $f(x) = x \log{x}$. To express divergence more accurately, this paper detects data availability by (12).

Parameter Settings. As described in [3], SVSM uses $50\%$ of all users to find frequent singleton items, $10\%$ to report the size of their itemsets that intersect with $CS$, and $40\%$ to update the frequent itemsets and their frequencies. Thus, we divide users into two parts, where $\eta$ is the percentage assigned in the first part. For fairness, we set $\eta = 0.5$, which implies that half of the users report frequent singleton items, while the other half update the estimated frequencies of the candidate frequent itemsets.

Selected Approaches for Evaluation of FO. The approaches used in the evaluation are as follows.

● Real-IHFO. The first phase returns the real FO, and the second and third phases use IHFO.

● Real-PSFO. The first phase returns the real FO, and the second and third phases use PSFO.

● Sample-IHFO. The first phase uses sampling (IFHO without perturbation), and the second and third phases use IHFO.

● Sample-Sampling. Both the first and second phases use sampling to obtain FO. It denotes the upper bound of UISM.

Selected Approaches for Evaluation of FIM. The approaches used in the evaluation are as follows.

● UIIM and UISM. Both the first and second phases use IHFO to obtain FO.

● SVIM and SVSM^[3]. The first phase uses PSFO (OLH, l = 1), and the second and third phases use PSFO (OLH, $l$ = adaptive$L$) to obtain FO.

● O-UIIM and O-UISM. It is an optimal version of UISM. The first phase uses PSFO (OLH, l = 1), and the second phase uses IHFO to obtain FO.

● PrivSet. The first phase uses PSFO (OLH, l = 1), and the second and third phases use Privset to obtain FO.

5.2   Evaluation of FO

In this subsection, we mainly compare the performance for frequency oracle.

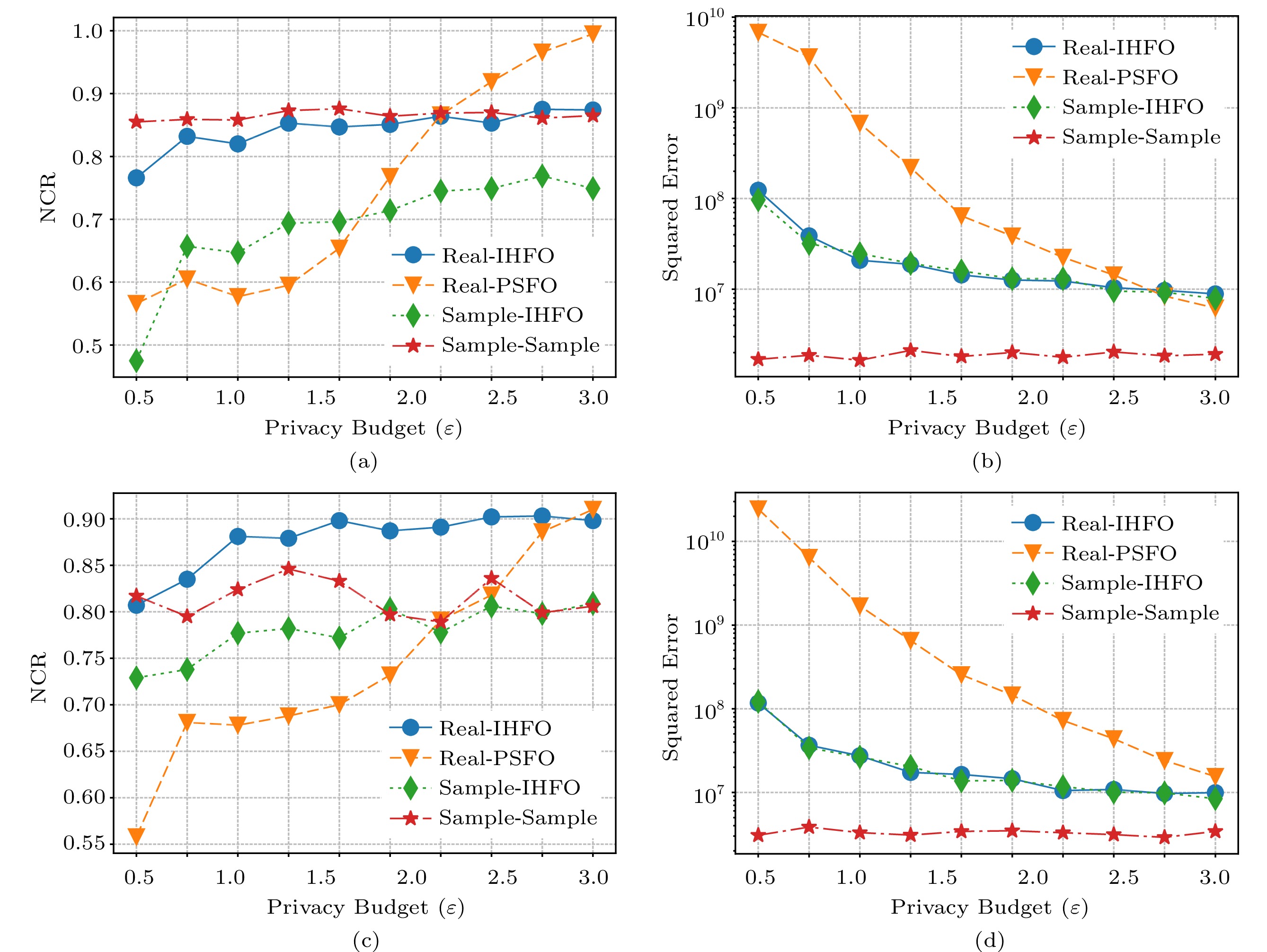
First, we compare Real-IHFO and Real-PSFO. In Fig.4(a) and Fig.4(c), the NCR trendlines of Real-IHFO show a stable performance, with a small increase as the privacy budget increases in Online and IBM. The NCR trendlines of Real-PSFO increase rapidly as the privacy budget increases and the results are better than those of Real-IHFO when the privacy budgets are large, but the exceeded point of IBM is larger than that of Online. A higher score indicates better identification. In Fig.4(b) and Fig.4(d), the trendlines of Real-IHFO are lower than those of Real-PSFO. A lower score denotes better frequency estimation. These indicate that: 1) as privacy budgets grow, the error caused by sampling in the IHFO algorithm is greater than that caused by perturbation; 2) the increase of the data size has a greater effect on IHFO than on PSFO, since the amount of the IBM data is greater than the amount of the online data; and 3) IHFO has a lower variance of frequency estimation.

Figure  4.  Performance under different protocols. (a) Online dataset, NCR (normalized cumulative rank), k = 64. (b) Online dataset, squared error, k = 64. (c) IBM dataset, NCR, k = 64. (d) IBM dataset, squared error, k = 64.

下载: 全尺寸图片 幻灯片

Second, we compare Real-IHFO and Sample-IHFO. The SE trendlines of them are close in Fig.4(b) and Fig.4(d). However, the NCR trendlines of Real-IHFO are much higher than those of Sample-IHFO in Fig.4(a) and Fig.4(c). These indicate that it is more useful in the first stage to obtain an accurate frequency ranking than a frequency estimation. Therefore, choosing PSFO ($l$ = 1) has advantages in O-UISM. In addition, the NCR of Real-IHFO and Sample-Sample shows that even if the perturbed collection is adopted in the second stage, the result reflects an advantage when the privacy budget is slightly larger.

Third, we compare Sample-IHFO and Sample-Sample. Fig.4(b) and Fig.4(d) show that the trendlines of Sample-Sample are far lower than those of all the other protocols regarding the squared error. They are also the upper bound errors that can be attained by UISM. Fig.4(a) shows the NCR on the Online dataset, Sample-Sample is always higher than that of Sample-IHFO. On the other hand, in Fig.4(c), the NCR on the IBM dataset is similar when the privacy budget is greater than 2. These indicate that the increase in the data size significantly affects IHFO.

In summary, this experiment shows that IHFO has a lower variance of frequency estimation and the dataset size has an obvious effect on IHFO.

5.3   Evaluation of FIM

In this subsection, we mainly compare the performance between our approaches and the state-of-the-art protocol for frequent item/itemset mining.

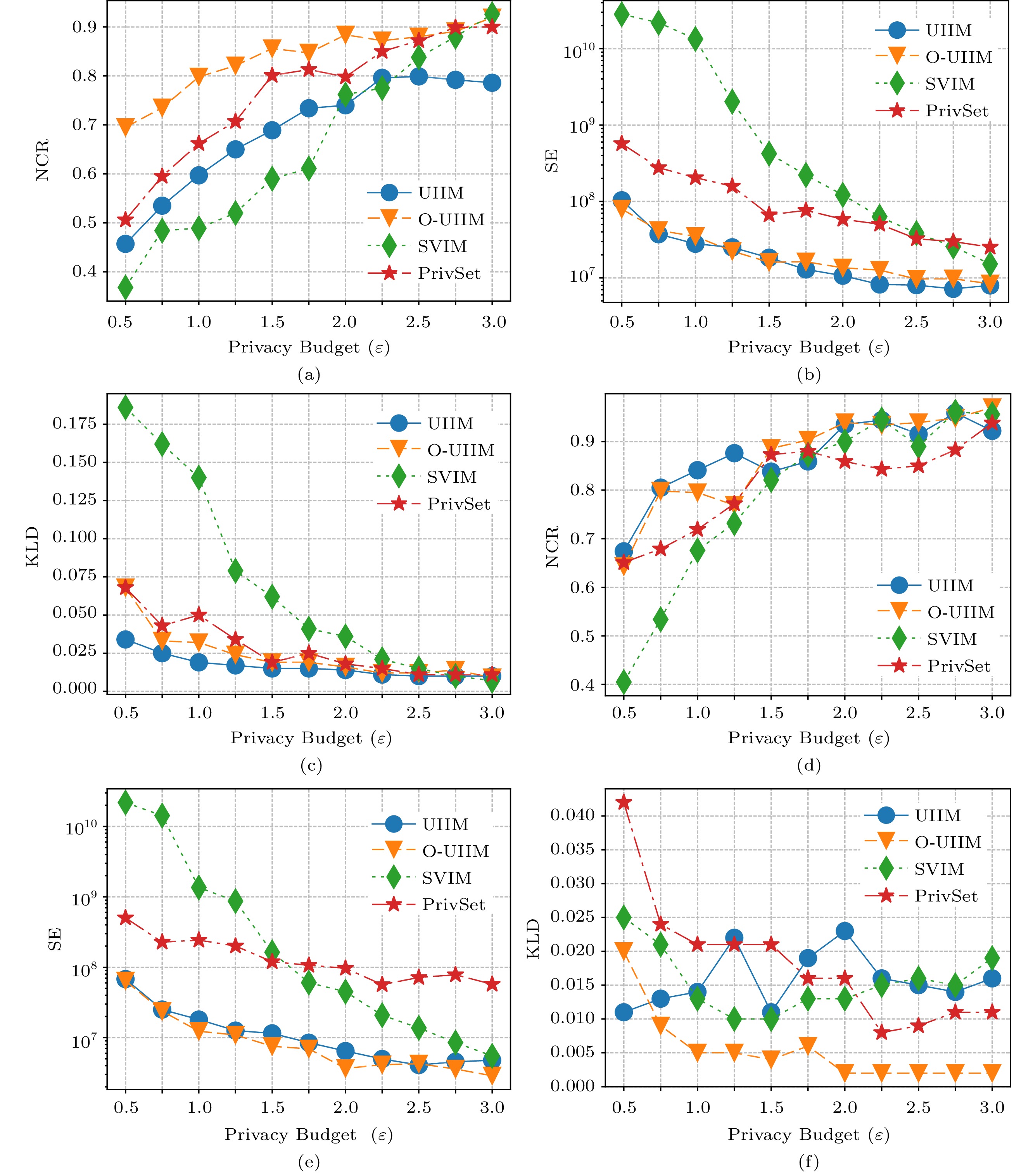
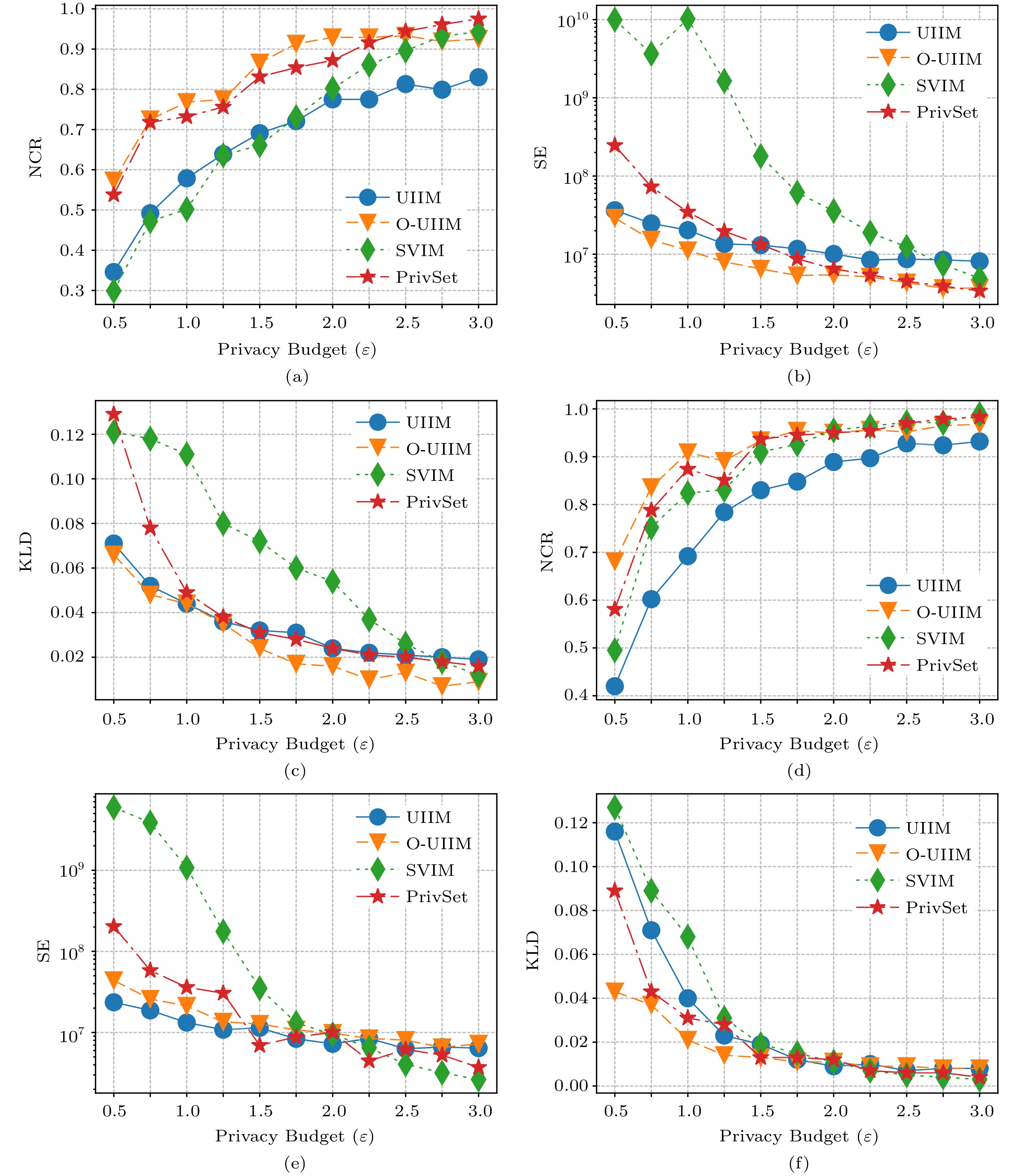
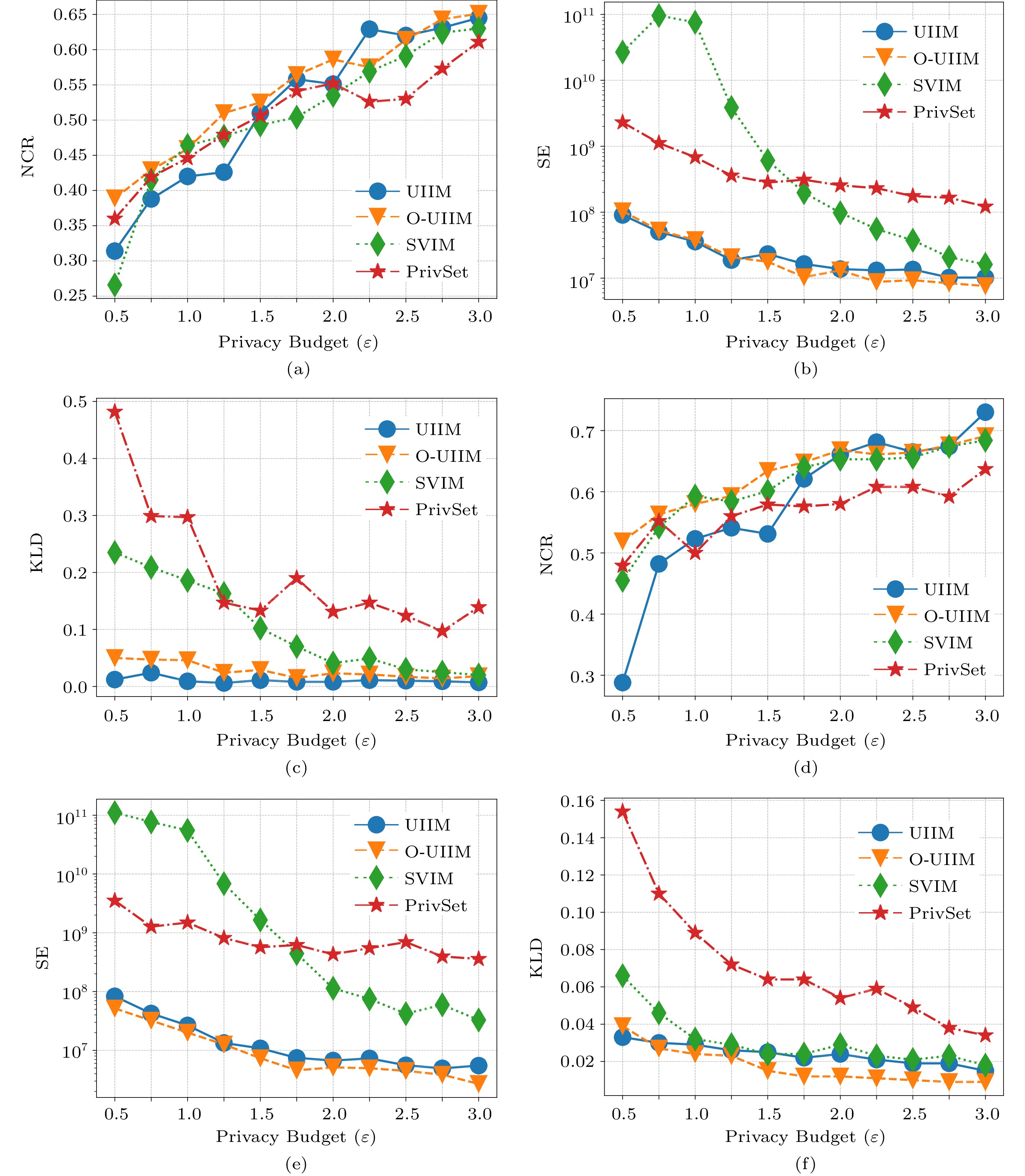
Singleton Frequent Items. We first identify the frequent singleton items in Fig.5 and Fig.6. First, Fig.5(a) and Fig.6(a) demonstrate the trendlines of NCR scores of all protocols when $k$ = 64. The trendlines of O-UIIM are the highest in most privacy budgets $\varepsilon$, and the score of SVIM is the highest at the last $\varepsilon$. A higher score indicates better identification. Figs.5(d) and 6(d) demonstrate the trendlines of NCR scores of all protocols when $k$ = 32. The trendlines of O-UIIM are the highest in most privacy budgets $\varepsilon$, and the scores of PrivSet are the highest at the last two $\varepsilon$. These results suggest that O-UISM performs the best in these metrics. Second, Figs.5(b), 5(e), 6(b), and 6(e) and Figs.5(c), 5(f), 6(c), and 6(f) demonstrate the trendlines of SE and KLD, respectively. The trendlines of UIIM and O-UIIM are lower in most privacy budgets $\varepsilon$ when $k$ = 64 and $k$ = 32. The reason for SVIM performing the best in several big privacy budgets is that the error caused by sampling in the IHFO algorithm is greater than that caused by perturbation. We combine SE and KLD for analysis because the frequency (SE) and distribution (KLD) of data are essential data availability standards. A lower score means a more accurate estimation. These results indicate that the UIIM and O-UIIM estimated data are more accurate. Third, NCR and SE are reviewed together in Figs.5(a) and 6(a) and Figs.5(b) and 6(b), respectively. A higher NCR and a lower SE imply that more items are identified with an estimation that is more accurate. Even though the SE score of UIIM is lower than that of O-UIIM, O-UIIM performs better because its NCR trendlines are notably higher than those of UIIM.

Figure  5.  Singleton identification for the IBM dataset. (a) IBM dataset, NCR (normalized cumulative rank), k = 64. (b) IBM dataset, SE (squared error), k = 64. (c) IBM dataset, KLD (Kullback-Leibler divergence), k = 64. (d) IBM dataset, NCR, k = 32. (e) IBM dataset, SE, k = 32. (f) IBM dataset, KLD, k = 32.

下载: 全尺寸图片 幻灯片

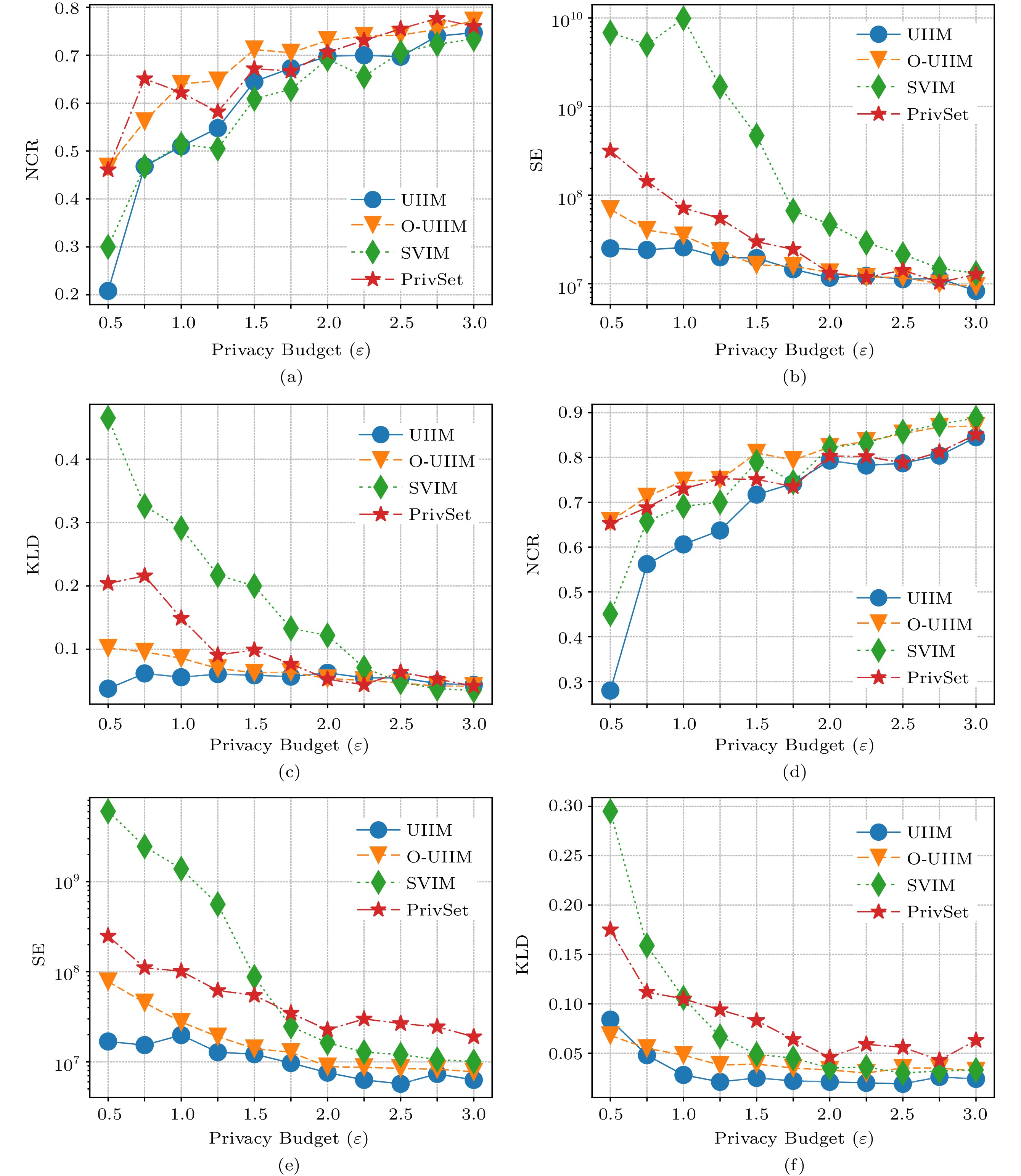
Figure  6.  Singleton identification for the Online dataset. (a) Online dataset, NCR, k = 64. (b) Online dataset, SE, k = 64. (c) Online dataset, KLD, k = 64. (d) Online dataset, NCR, k = 32. (e) Online dataset, SE, k = 32. (f) Online dataset, KLD, k = 32.

下载: 全尺寸图片 幻灯片

Itemset Mining. We evaluate the effectiveness of our protocols on frequent itemset mining. The results are similar to the results of frequent singleton items. First, Figs.7(a) and 8(a) and Figs.7(d) and 8(d) demonstrate the trendlines of NCR scores of all protocols when $k = 64$ and $k = 32$, respectively. The trendlines of O-UISM are the highest in most privacy budgets $\varepsilon$. A higher score indicates better identification. These suggest that O-UISM performs the best in these metrics. Second, Figs.7(b), 7(e), 8(b), and 8(e) and Figs.7(c), 7(f), 8(c), and 8(f) demonstrate the trendlines of SE and KLD, respectively. The trendlines of UIIM and O-UIIM are lower in most privacy budgets $\varepsilon$.

Figure  7.  Itemset mining results for the IBM dataset. (a) IBM dataset, NCR, k = 64. (b) IBM dataset, SE, k = 64. (c) IBM dataset, KLD, k = 64. (d) IBM dataset, NCR, k = 32. (e) IBM dataset, SE, k = 32. (f) IBM dataset, KLD, k = 32.

下载: 全尺寸图片 幻灯片

Figure  8.  Itemset mining results for the Online dataset. (a) Online dataset, NCR, k = 64. (b) Online dataset, SE, k = 64. (c) Online dataset, KLD, k = 64. (d) Online dataset, NCR, k = 32. (e) Online dataset, SE, k = 32. (f) Online dataset, KLD, k = 32.

下载: 全尺寸图片 幻灯片

We can also see that the trendlines of O-UIIM start and rise quickly and level off since $\varepsilon>1.75$. This indicates that O-UISM performs the best when $\varepsilon$ is not large, and O-UISM cannot offset the error caused by the Hadamard encoding and sampling with increasing privacy budget. Moreover, UISM does not perform as well as O-UISM in NCR under different privacy budgets but performs well in SE and KLD. This indicates that the IHFO algorithm is good at updating frequent itemsets and their corresponding frequencies.

In summary, this experiment shows that O-UISM performs the best in FIM.

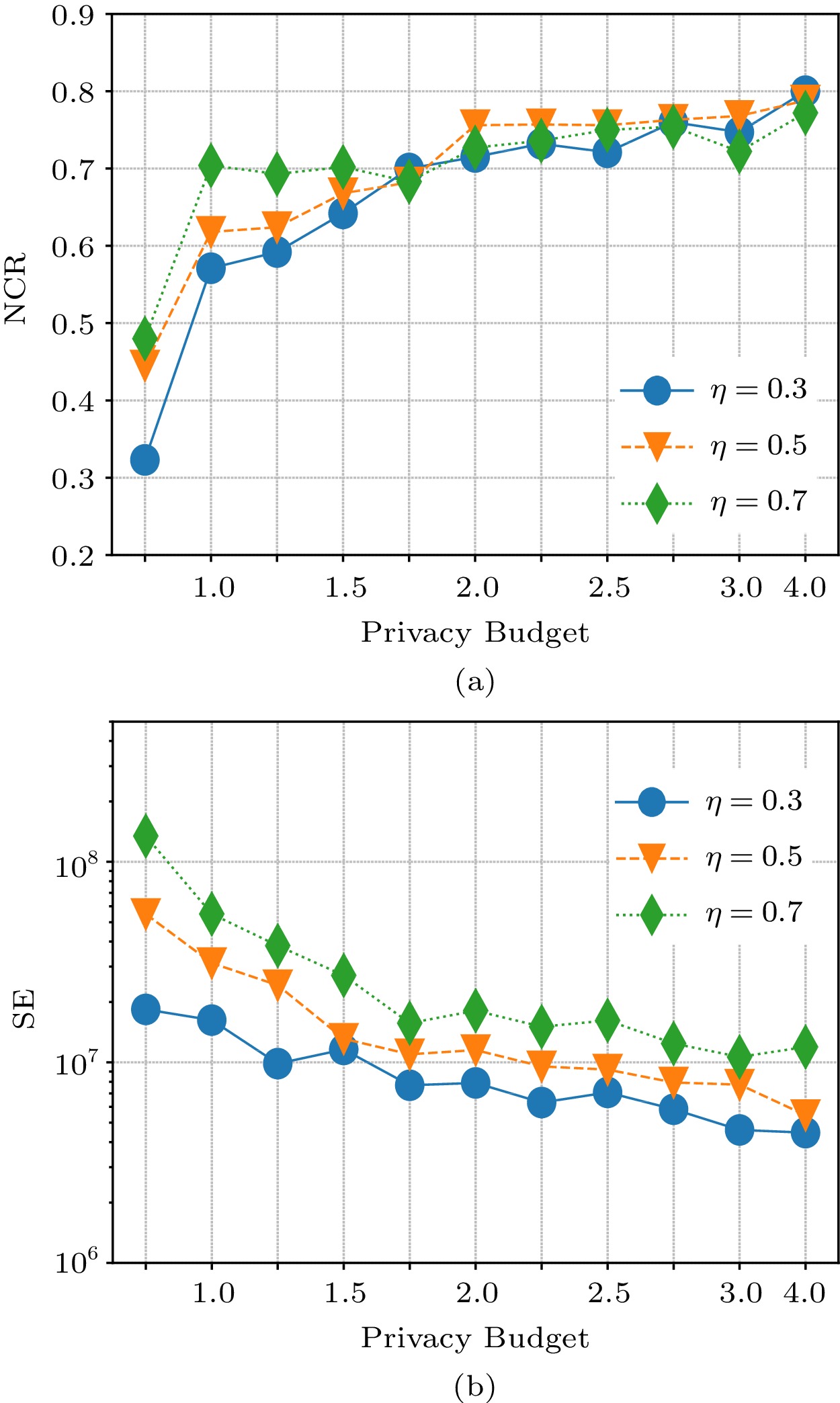
Different $\eta$. Fig.9 shows the impact of the dataset division $\eta$ which means the aggregator applies the percent to obtain the rank of the items in the first part of the dataset. If $\eta$ is small, fewer data in the first part are applied to identify frequent singleton items. If the amount of data in the second part is less, the squared error is higher under the same privacy budget. Trendlines of NCR are interwoven to different $\eta$. We consider $\eta = 0.5$ to be the appropriate choice.

Figure  9.  (a) NCR and (b) SE of varying dataset division $\eta$ under different $\varepsilon$.

下载: 全尺寸图片 幻灯片

6.   Conclusions

In this study, we investigated LDP (local differential privacy) approaches for FIM (frequent itemset mining) when each user transaction has a set of items whose length is varied. One natural LDP algorithm (e.g., SVSM) is for each user to sample only one item and use a known algorithm to send, which should balance the bias and variance. We sacrificed non-sensitivity privacy to develop an unbiased approach for FIM while protecting the privacy of items in each transaction. In most cases, our approach results in the lowest variance, ensuring the most accurate outcome. We theoretically and experimentally demonstrated that the proposed FIM approach, O-UISM, significantly outperforms the extant approaches in finding frequent itemsets and estimating their frequencies under the same privacy guarantee.