基于图卷积和循环神经网络的城市服务设施时空位置推荐
Spatio-Temporal Location Recommendation for Urban Facility Placement via Graph Convolutional and Recurrent Networks
-
摘要:
POI服务设施的选址规划是城市计算的重要内容,良好的选址能为居民的工作生活带来便利,提高POI设施的服务效率,还能缓解城市的交通和环境等压力。现阶段大部分城市都已经发展到了一定的阶段,相应的服务设施都存在于城市的不同区域中。因此,选址工作不仅要考虑时空域上城市居民对候选地址的影响力,还要综合分析已经存在的服务设施对候选地址的影响效应,以及新建设施对现存设施的影响等因素。为此,本文提出了半监督环境下的选址模型STGCRN。该模型首先以地址为中心,将城市区域分块划分并提取对应的多维度特征,以此为基础构建地址关联图。然后,引入基于多头注意力机制的上下文图卷积模块对地址设施的空间关联关系建模,捕获地址的局部空间相关性和全局空间相关性,并采用循环神经网络对地址设施的动态时间依赖关系建模,捕获周期性时间片内流行度的前后依赖性。最后,分别从空间域和时间域预估地址缺失的流行度分布,使用熵机制融合后,与时空特征一并再次送入循环神经网络模块,获得最终的候选地址流行度用于选址推荐。在两个实验数据集中的共计6类具体服务设施上,本文所提预测模型STGCRN的性能都优于其他的比较算法。因为STGCRN重点分析和提取了城市区域内用户群体的时空轨迹特征和社交关联等特征,在半监督的环境下,采用基于多头注意力机制的上下文图卷积模块建模地址的空间局部相关性和空间全局相关性,并使用LSTM模块捕捉地址的动态时间依赖关系,从而解决了候选地址流行度预测中所面临的用户自相关、空间自相关和时间自相关等难题。本文充分挖掘了用户签到、行程轨迹和社交行为等数据,与时空域结合得到的预测结果准确科学,在此基础上根据预测结果进行的增量选址,效率高、效果好,本研究可以为各类城市服务设施的选址提供理论支撑和算法参考。
Abstract:The ability to recommend candidate locations for service facility placement is crucial for the success of urban planning. Whether a location is suitable for establishing new facilities is largely determined by its potential popularity. However, it is a non-trivial task to predict popularity of candidate locations due to three significant challenges: 1) the spatio-temporal behavior correlations of urban dwellers, 2) the spatial correlations between candidate locations and existing facilities, and 3) the temporal auto-correlations of locations themselves. To this end, we propose a novel semi-supervised learning model, Spatio-Temporal Graph Convolutional and Recurrent Networks (STGCRN), aiming for popularity prediction and location recommendation. Specifically, we first partition the urban space into spatial neighborhood regions centered by locations, extract the corresponding features, and develop the location correlation graph. Next, a contextual graph convolution module based on the attention mechanism is introduced to incorporate local and global spatial correlations among locations. A recurrent neural network is proposed to capture temporal dependencies between locations. Furthermore, we adopt a location popularity approximation block to estimate the missing popularity from both the spatial and temporal domains. Finally, the overall implicit characteristics are concatenated and then fed into the recurrent neural network to obtain the ultimate popularity. The extensive experiments on two real-world datasets demonstrate the superiority of the proposed model compared with state-of-the-art baselines.
-
1. Introduction
The recent research of urban planning focuses primarily on identifying appropriate new geographical locations for placing service facilities (e.g., supermarket, vehicle charging station, and coffee shop), especially in the fact that congener facilities have already been established in urban regions. According to the corresponding facility placement expectation, both service providers and urban dwellers will gain significant benefits, including a prosperous economy, convenient life, and smooth traffic. Many essential factors should be considered in recommending candidate locations in urban areas, but one of the most important factors is the profit of the facility placement. Establishing a particular service facility at different locations will lead to varied incomes. For instance, opening new fast-food restaurants near business districts or railway stations can yield higher profits than those located in residential areas. Therefore, before deciding where to place new facilities, it is necessary to appraise the profits incurred along the time on these candidate locations.
In this paper, popularity is seen as the reflection of profits or earnings intuitively for a particular facility's location recommendation, which is measured by the number of customers who are served. Specifically, facility popularity is formally quantified by the number of customer check-ins during a certain period on location-based social networks (e.g., Weibo, Douban, and Twitter). Consequently, the potential popularity of candidate locations can facilitate the determination of location selection for service facility placement, namely, incremental candidate location recommendation (ICLR). For instance, as shown in Fig.1, there are two candidate locations, A and B, for a new Starbucks in an urban area where five Starbucks exist with their historical popularity in terms of month-by-month check-in records available. Therefore, ICLR aims to predict potential monthly popularity for the most profitable location based on the corresponding historical data and other relevant characteristics. Further, a more profitable time node can also be predicted, such as certain seasons and months.
Many efforts have been put into location recommendations. The most commonly used model of popularity prediction is feature engineering, whose rationale is that locations with similar characteristics tend to have closer popularity. Traditional approaches are usually based on the features of location geography and user mobility[1–3]. In recent studies, analyzing characteristics from different location-based online services has attracted much more attention[4-8], such as check-in records[5], social preferences[6], and transitional trajectories[8]. Despite the significant progress brought by recent research, it is a non-trivial task to predict the popularity transformations over time or within a time period (e.g., month by month, or national holidays), due to the difficulty in capturing the spatio-temporal correlations among locations themselves or between candidate locations and existing facilities, as well as the incompleteness and scarcity of location characteristics. To sum up, we need to resolve the following three significant challenges.
1) Customer Effect. The spatio-temporal effects for location popularity are implicitly made by urban dwellers (facility customers). In addition to the conventional features (e.g., residential place, daily travel trajectory, and POI check-in), social relationship is also one of the essential factors affecting the choices of service facility locations on online social networks, such as reciprocal recommendation or internet celebrity economy.
2) Spatial Correlation. The non-linear spatial correlations rest among locations. The location popularity is not only explicitly affected by the occupancy of both candidate locations and existing facilities nearby, but can also have implicitly irregular correlations with distant facilities. For example, two facilities far away from each other can have comparable popularity if the regional environments are similar.
3) Temporal Dependency. The dynamic temporal correlations exist within the locations themselves. Future popularity of candidate locations is auto-depended on their popularity in previous time periods. In addition, customer effect and spatial correlation can vary over time, which makes the dependencies even harder to capture.
In recent years, deep learning has been widely employed to model high-dimensional spatio-temporal data. For example, Graph Convolutional Network (GCN) extends the well-known Convolutional Neural Network (CNN) to a non-Euclidean graph structure. The latent representation of each graph node in GCN is evolved by aggregating and then propagating representations of its various neighbors[9]. In addition, Recurrent Neural Network (RNN)[10] and its successors, e.g., Long-Short-Term-Memory (LSTM) network[11] and Gated Recurrent Unit (GRU) network[12], are initially proposed to solve natural language processing problems, as they can be directly employed to effectively learn complicated schemes from a large amount of sequential information. Therefore, these useful technologies can be introduced into the recommendation of candidate locations. Specifically, graph nodes serve as locations, and edges represent spatial correlations between pair-wise locations. Both the spatial characteristics and temporal impacts can be well modeled for popularity prediction.
This paper aims to address these aforementioned problems with the help of GCN and RNN, by proposing the Spatio-Temporal Graph Convolutional and Recurrent Networks (STGCRN) framework for popularity prediction and location recommendation, where congener facilities have already been established and their historical popularity is available. Specifically, the main contributions of our work are summarized as follows.
● With the significant consideration of spatio-temporal trajectories and online social services of dwellers, we partition the urban space into spatial regions centered by locations, and extract the corresponding multi-dimensional characteristics from existing facilities, candidate locations, and regional dwellers. Based on these we develop the location correlation graph.
● We introduce a novel semi-supervised spatio-temporal learning model to incorporate graph characteristics and historical popularity of existing facilities based on the location correlation graph, whose goal is to predict the popularity of candidate locations over time to facilitate the geographical placement of new facilities.
● We propose an attention mechanism based contextual graph convolution module to incorporate both local and global spatial correlations among locations, and also introduce an RNN to capture the dynamic temporal dependencies. Furthermore, a popularity approximation block is employed to estimate the missing popularity from both spatial and temporal domains.
● Extensive experiments are carried out on two real-world datasets from Beijing and New York, which all verify that our model significantly achieves the best prediction performance compared with state-of-the-art baselines.
The rest of the paper is organized as follows. We review related work in Section 2, and present some preliminary concepts and formulate the location recommendation problem in Section 3. We introduce the pre-processing of inputs in Section 4. The proposed model is discussed in more detail in Section 5. The experiments are conducted in Section 6, and the paper is concluded in Section 7.
2. Related Work
2.1 Location Recommendation
Facility location recommendation identifies the optimal candidate locations to set up new service facilities for dwellers of cadidate locations, according to the primary selection criterion of the popularity of each candidate location. Karamshuk et al.[1] first formally proposed the popularity to rank all candidate locations for the best retail store placement, using a linear model to evaluate popularity by recognizing geographic and user mobility features and translating them into scores. Li et al.[13] first introduced dweller trajectories to appraise a candidate location based on the number of potential customers it can attract, for which each trajectory is assigned a score according to a distribution model. Mitra et al.[14] developed Trajectory-Aware Optimal Placement of Services (TOPS) that selects the best k candidate locations on the road network to optimize a wide class of objective functions defined over dweller trajectories. They proved that TOPS is NP-hard and accordingly developed a multi-resolution clustering-based approximation framework of NetClus. Mitra et al.[4] further extended TOPS to Trajectory-Aware Inconvenience-Minimizing Placement of Services (TIPS), aiming to minimize the dweller inconvenience in trajectory-aware service placement.
Furthermore, Ma et al.[6] and Wang et al.[7] incorporated both geographical and categorical preferences of candidate locations, and especially considered the effect of social relationships among online service customers for ultimate popularity prediction. For the next optimal restaurant placement, Wang et al.[2] additionally took advantage of customer reviews to construct predictive characteristics, and incorporated them into a regression model to predict the number of check-ins that a candidate location would likely attract. Li et al.[15] only recognized the unique trajectories that directly pass by the locations to identify the most influential k candidate locations for facility placement. However, these above approaches ignore the primary temporal dependencies among locations, where the recommended locations may vary at different time periods.
Recently, Hsieh et al.[5] devised a semi-supervised learning model API, which predicts the temporal popularity of candidate locations for retail store placement. API first defines a set of location affinity functions for each relevant feature and then constructs the location affinity graph to model spatial and temporal correlations among locations, and is finally implemented by Gaussian random fields. Although both spatial and temporal correlations are considered, API fails to incorporate them into a unified framework to improve recommendation accuracy.
In addition, Ruan et al.[16] formulated the dynamic allocation problem of public resources in a small area (e.g., trash bins in an amusement park), and the proposed MALMCS framework employs matrix factorization for spatio-temporal neural networks (MF-STN)[17] to predict crowd flows. MF-STN captures spatio-temporal correlations between urban regions by a spatio-temporal (ST) feature learner and then leverages the learned latent characteristics to make predictions within a specific region. Hsieh et al.[18] designed the GEM framework for air quality prediction, which utilizes existing monitoring data and heterogeneous city dynamics, such as meteorology, human mobility, road network structure, and urban POIs.
Zheng et al.[19] proposed a semi-supervised learning approach to infer real-time and fine-grained urban air quality, where an artificial neural network and a linear-chain conditional random field are adopted to resolve spatial and temporal features, respectively. For the next POI recommendation that people will visit in future trips, Liu et al.[20] proposed ST-RNN by extending RNN. ST-RNN models time intervals in a recurrent architecture, and incorporates distance-specific transition matrices for modeling geographical distances. Luo et al.[21] developed STAN, a bi-layer attention architecture that aggregates spatio-temporal correlation in trajectories and recalls the targets with the help of personalized item frequency for POI recommendation. Although these studies are not directly relevant to the popularity prediction of locations, we can consider the dynamic allocation and air quality prediction as a special kind of recommendation problem under study.
2.2 Graph Convolutional and Recurrent Network
GCN-based models are generally more progressive and flexible than purely CNN-based approaches. Due to its remarkable effectiveness, GCN has been successfully applied to several spatio-temporal forecasting tasks with the help of a recurrent neural network. Zheng et al.[22] predicted the transportation requests by Spatial-Temporal Graph Convolutional Sequential Learning (ST-GCSL) across different positions and time slots. It builds a granular model within both the spatio-temporal gate block and clustering context feature sequence. As for traffic flow prediction, Wang et al.[23] proposed a novel spatio-temporal graph neural network, which can comprehensively capture spatial and temporal patterns by a learnable positional attention mechanism and a sequential component, respectively. Zhang et al.[24] further designed SHARE for predicting city-wide parking availability whose main advantages lie in a hierarchical graph convolutional structure and a GRU-based recurrent neural network. In addition, they developed an approximation module to estimate missing real-time parking availability. By considering temporal properties of traffic flows, i.e., recent, daily-periodic, and weekly-periodic dependencies, Guo et al.[25] used the ASTGCN model to solve traffic flow forecasting problems, where the temporal dependencies are also implemented by the attention mechanism of GCN.
Moreover, Bai et al.[26] investigated the challenges of passenger demand over multiple time horizons and then present STG2Seq, a multiple hierarchical gate graph convolution module with two attention mechanisms, to simultaneously capture both spatial and temporal correlations. Geng et al.[27] performed a regional demand forecast of accurate ride-hailing, ST-MGCN. It first encodes pair-wise correlations among regions into multiple graphs and then explicitly models them by multi-graph convolution. Finally a GRU block is employed to re-weigh different historical characteristics.
Liu et al.[28] proposed HMTRL, a unified route representation learning framework for multi-modal transportation recommendation, where both the spatio-temporal dependencies in transportation networks and the semantic coherence of historical routes are exploited. Wang et al.[29] introduced a knowledge graph with temporal information into POI recommendation and then devised the framework of STGCAN, to learn user preferences by dynamically capturing the spatio-temporal neighborhoods. For effective traffic flow forecasting, Li and Zhu[30] proposed STFGNN, which learns hidden spatio-temporal dependencies by a novel fusion operation, and handles long sequences with the help of an integrated graph module and a gated convolution module. Consequently, these above concrete studies on the graph convolutional and recurrent network in request predictions make the graph convolutional and recurrent network credible in the practice of spatio-temporal location recommendation.
Despite the great contributions of the existing researches, there has been a lack of practical work on spatio-temporal popularity prediction and location recommendation for urban facility placement from a comprehensive perspective. Therefore, we propose the novel model STGCRN based on the graph convolutional and recurrent network, whose effectiveness and stability are significantly guaranteed.
3. Preliminaries
In this section, we present the notations used throughout the paper in Table 1, provide a range of definitions, formulate the recommendation problem, and present an overview of the proposed model.
Table 1. Definition of NotationsNotation Definition l Particular location τ Route trajectory Gs Social network X Contextual characteristics Y Historical popularity ˜y Predicted popularity F(⋅) Mapping function r Urban region G Location correlation graph Si(ri,rj) Semantic similarity of ri and rj {{\boldsymbol{x}}}_{l_i}^{l,t} Local spatial implicit feature {{\boldsymbol{x}}}_{l_i}^{g,\ t} Global spatial implicit feature {{\boldsymbol{h}}}_{l_i}^{t} Temporal hidden state {{{\boldsymbol{y}}}}_{l_i}^{{\rm sdl},\ t} Local spatial popularity {{{\boldsymbol{y}}}}_{l_i}^{{\rm sdg},\ t} Global spatial popularity {\boldsymbol{y}}_{l_i}^{{\rm td},\ t} Approximated temporal popularity \boldsymbol{y}_{l_i}^{f,\ t} Fused popularity distribution 3.1 Definitions and Problem Statement
To begin with, an undirected graph G_r = (V_r, E_r, \boldsymbol W_r) is introduced to represent an urban space with numerous inhabits and the corresponding road network. V_r is the set of road intersections (nodes), E_r denotes the set of road segments (edges), and \boldsymbol W_r is the symmetric weight matrix. Each edge e(u,v) \in E_r has a positive weight w(u,v) \in \boldsymbol W_r , i.e., actual spatial distance.
Definition 1 (Location). A location l \in L is a particular site where a specific service facility has already been established or will be as planned in specific urban areas. We denote a set of locations L = L_l \cup L_u = \{l_1,l_2,\ldots,l_m\} , L_l \ne L_u , where m is the total number of locations, L_l and L_u represent a set of locations with and without facilities, respectively, and l \in L_u is referred to as a candidate location.
Definition 2 (Trajectory). A trajectory \tau \in \Gamma illustrates the daily travel pattern of the dweller in the road network, which is described in the sequential forms of \tau = \{(p_1,t_1),(p_2,t_2),\ldots,(p_\zeta,t_\zeta)\} , where p_i represents a specific geographical position at a road segment (including road intersection) collected by GPS-liked devices, and t_i denotes the corresponding timestamp when the dweller passing by, t_i < t_j , if i<j , 1 \leqslant i,j \leqslant \zeta .
Definition 3 (Social Relationship). The online social relationships among urban dwellers are defined by a directed graph G_s = (V_s, E_s) in the location-based social network, where V_s is the set of dwellers (customers), and E_s represents the set of edges. Each edge e(u,v) \in E_s from node u to v denotes that u has followed v with a positive weight of 1.
Definition 4 (Popularity). The popularity y_{{l_i} \circ {t_j}} of the candidate location l_i for a particular facility represents the prospective number of customers who will consume there in a future time period t_j .
Note that the location popularity of an existing facility is indicated by the number of historical check-ins made by customers in a certain time period.
Definition 5 (Location Popularity Prediction). Given historical consecutive time steps T_{\rm h} , a set of contextual characteristics for all locations {\cal{X}}_{L \circ {T_{\rm h}}} = \{{{{\boldsymbol{X}}}^{t - T_{\rm h} + 1}},{{\boldsymbol{X}}^{t - T_{\rm h} + 2}},\ldots,{{\boldsymbol{X}}^t}\} , and a set of historical popularity {\cal{Y}}_{{L_l} \circ {T_{\rm h}}} = \{ {\boldsymbol{Y}}_{L_l}^{t - T_{\rm h} + 1} , {\boldsymbol{Y}}_{L_l}^{t - T_{\rm h} + 2},\ldots,{\boldsymbol{Y}}_{L_l}^t\} for L_l , location popularity prediction is to calculate the future popularity for candidate locations L_u over the next consecutive periods T_{\rm f} :
{\cal{F}}({\cal{X}};{\cal{Y}}_{{L_l} \circ {T_{\rm h}}} ) \to ( \hat{{\boldsymbol{Y}}}_{{L_u}}^{t + 1},\hat{{\boldsymbol{Y}}}_{{L_u}}^{t + 2},\ldots,\hat{{\boldsymbol{Y}}}_{{L_u}}^{t + T_{\rm f} }), where {\cal{F}}( \cdot ) is the mapping function that needs to be learned, and \hat{{\boldsymbol{Y}}}_{{L_u}}^{t + i} is the predicted popularity, 1 \leqslant i \leqslant T_{\rm f} , and T_{\rm f} > 1 .
Definition 6 (The ICLR Problem). Given an urban area within the road network G_r , all the locations L , the multi-dimensional features {\cal{X}}_{L \circ {T_{\rm h}}} , the historical popularity {\cal{Y}}_ {{L_l} \circ {T_{\rm h}}} , and the dwellers U with both the corresponding trajectories \Gamma and social relationships G_s , the ICLR problem seeks to select the optimal candidate locations {\cal{L}}_{u \circ t}^k \subset L_u in a future period t , | {{\cal{L}}_{u \circ t}^k} | = k , which will obtain the maximum popularity when establishing a specific type of facility in those candidate locations.
3.2 Framework Overview
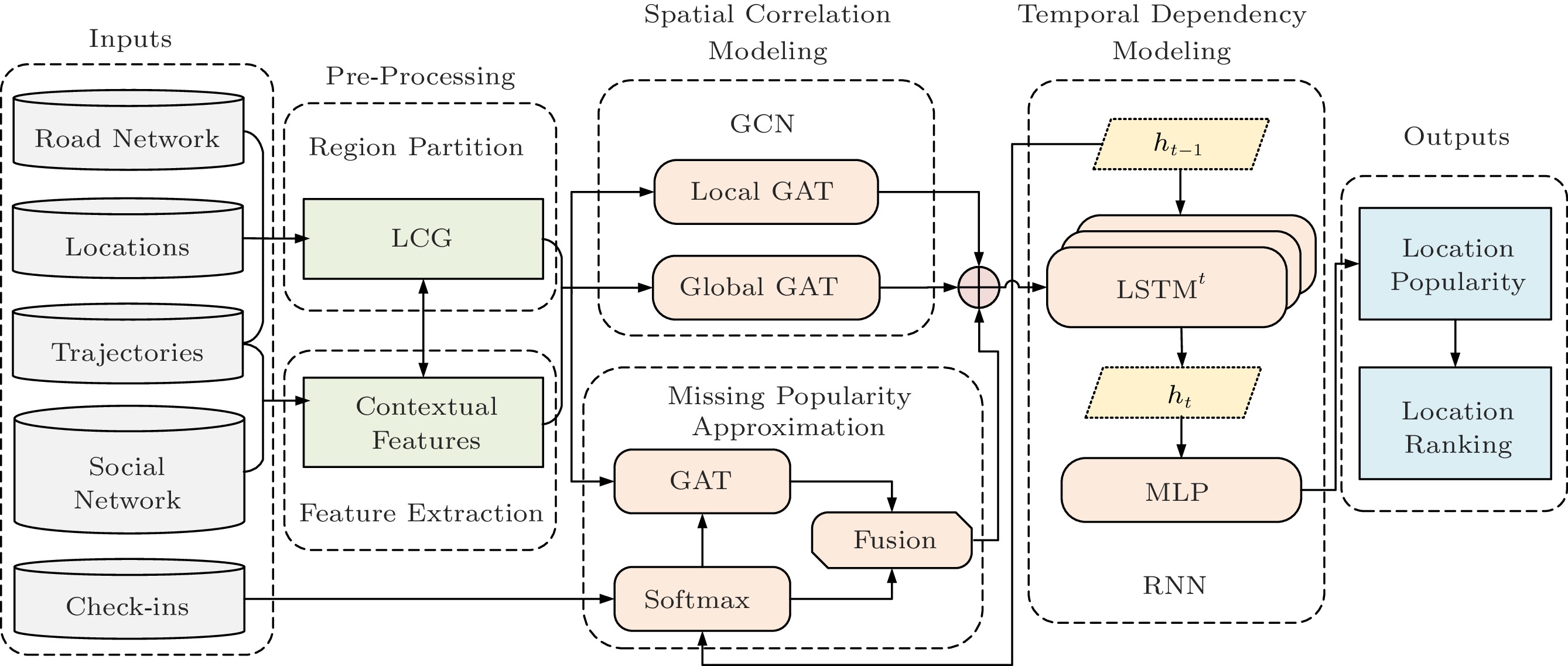
The framework of STGCRN is shown in Fig.2, where the inputs are the multi-dimensional characteristics of all locations and historical check-ins of existing facilities, and the outputs are the predicted popularity of candidate locations in future periods. Specifically, it includes five major components.
First, for data pre-processing, the urban space is partitioned into spatial regions, where there is only one location in each region. The contextual features are extracted from locations and regional dwellers, and subsequently the location correlation graph is developed. Second, a graph convolutional module is proposed to model spatial correlations among locations. Both the local and global spatial correlations are captured by two multi-head attention mechanism based graph convolutional blocks. Third, a recurrent neural network module is introduced, employing the LSTM blocks to model the dynamic temporal dependencies inside the locations themselves. Fourth, an approximation block is employed to estimate the probabilistic distributions of missing popularity from spatial and temporal domains. In the spatial domain, a multi-head attention mechanism based graph convolutional block is additionally utilized to propagate the observed popularity to the missing popularity based on the contextual similarity of locations. In the temporal domain, the LSTM blocks are reused to approximate the current popularity distributions based on their previous outputs. Subsequently, the two estimated popularity results are integrated through an entropy-based mechanism and then concatenated with both local and global spatial characteristics. Fifth, the previous concatenated characteristics are fed into the LSTM blocks to generate the ultimate popularity for location recommendation.
4. Pre-Processing
This section introduces the data pre-processing of STGCRN in detail, including region partition, feature extraction, and location correlation graph construction.
4.1 Region Partition
The intuitive consideration of region partition is that urban dwellers are more prone to access services from nearby facilities, e.g., shopping in a nearby mall, or dining within walking distance. Therefore, it can easily form the agglomeration effects centered by the location in the road network.
Definition 7 (Urban Region). An urban region r \in R is illustrated as a spatial complex that consists of a location and a neighborhood area. There are also many different kinds of facilities that provide a variety of urban functions and living services for dwellers.
As aforementioned that a location corresponds to an urban region one-to-one, we partition the urban space into a two-level structure considering urban characteristics and dweller mobility.
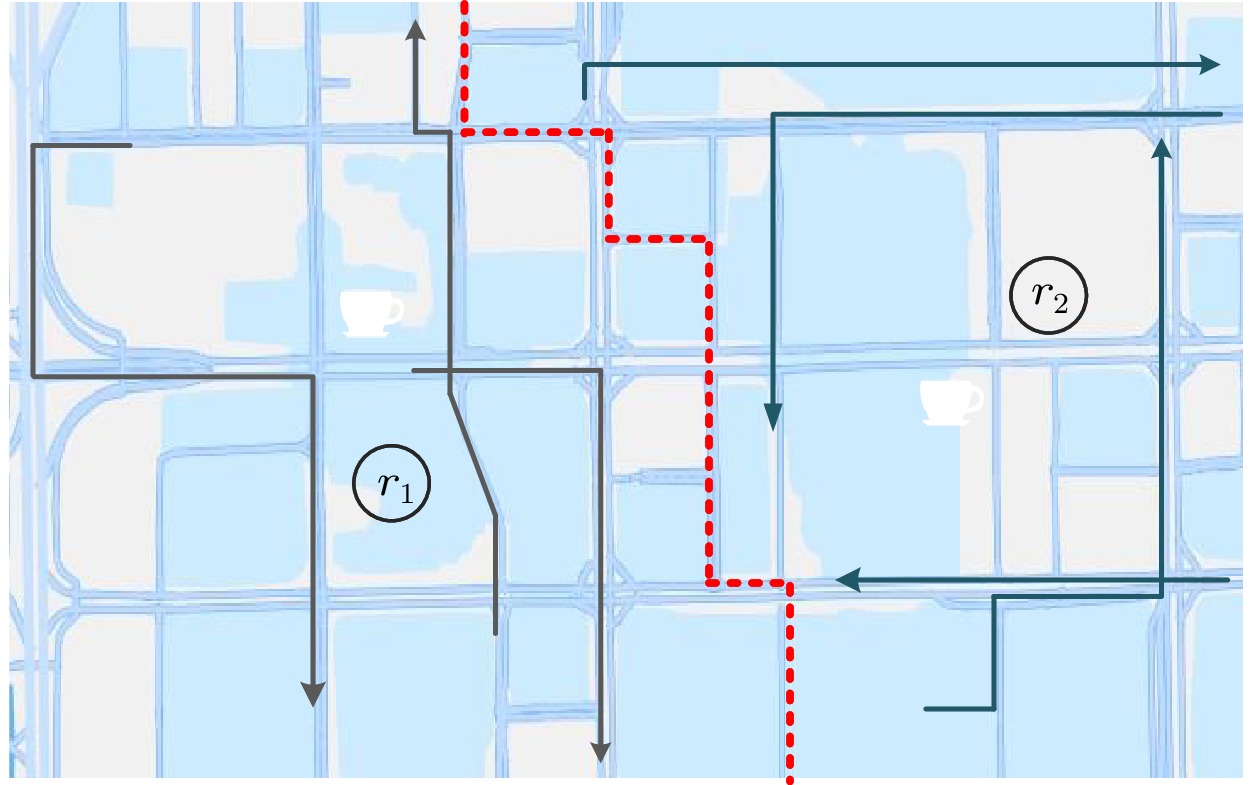
For the first level, the urban area is partitioned into sub-areas based on lower administrative boundaries. The intuitions are that the urban planning can differ in these administrative regions, and the functionalities of each region are usually different, but the living patterns of dwellers in the same region are generally similar. For the second level, we continue to partition the first-level sub-areas by applying a k -Medoids based approach[31] according to locations, dweller trajectories, and road networks, and then obtain \kappa regions, where \kappa is the number of locations in this urban space. Specifically, we first cluster all trajectories to the nearest location according to the metric of the shortest spatial distance between trajectories and locations in the road network. Then we partition two neighboring clusters by the road edges with the average minimum intervals to their corresponding outer trajectories. The intuition is similar to the classification principle of the Support Vector Machine (SVM)[32].
An example is illustrated in Fig.3, where two coffee shops and seven dweller trajectories (solid lines) are located. According to the two-level partition method, the road edges coverd with dotted lines are the partition boundary between regions r_1 and r_2 .
4.2 Feature Extraction
The candidate location recommendation is highly contextualized. Therefore, four typical views are chosen to capture the features of the regional contexts: spatio-temporal trajectory, social relationship, public transportation, and similar facility. These views return multiple scores corresponding to quality assessment in each of the time periods.
4.2.1 Spatio-Temporal Trajectory
We consider the two most relevant features: the numbers of inflow and outflow of crowds, as well as their corresponding distributions of spatial distances between trajectories and locations.
Specifically, given an urban region r_i within the location l_i , the corresponding inflow of trajectories in time period t \in [t^s,t^e] can be denoted as the set of \Gamma _{\rm in}^t({r_i}) , for each trajectory \tau = \{(p_1,t_1),(p_2,t_2),\ldots, (p_\zeta,t_\zeta)\} , \tau \in \Gamma _{\rm in}^t({r_i}) , iff \tau \in \Gamma , {p_{j - 1}} \notin {r_i} \wedge {p_j} \in {r_i} , and t_j \geqslant t^s , j > 1 , where t^s and t^e are the starting and ending timestamps in time period t , respectively. Similarly, the outflow of crowds in time period t is illustrated as the set of \Gamma _{\rm out}^t({r_i}) , for each \tau \in \Gamma _{\rm out}^t({r_i}) , iff \tau \in \Gamma , {p_{j }} \in {r_i} \wedge {p_{j+1}} \notin {r_i} , and t_j \leqslant t^e , j > 0 . Therefore, the features of the inflow and outflow of crowds of region r_i in time period t can be represented as:
{N_{\rm in}^{t}({r_i}) } = | {\Gamma_{\rm in}^{t}({r_i}) } |,{N_{\rm out}^{t}({r_i}) } = | {\Gamma_{\rm out}^{t}({r_i}) } |. Meanwhile, the shortest spatial commuting distance from trajectory \tau_j to location l_i is defined as:
{d_{\rm m}}({l_i},{\tau_j}) = {\min \limits_{\forall p_j^k,\,p_j^\iota \in {\tau_j}}}\{ {d_{\rm s}}(p_j^k,{l_i}) + {d_{\rm s}}({l_i},p_j^\iota) - {d_{\rm a}}(p_j^k,p_j^\iota)\}, (1) where {d_{\rm s}}(p_j^k,{l_i}) is the shortest spatial distance from p_j^k to {l_i} in the road network, and {d_{\rm a}}(p_j^k,p_j^\iota) is the spatial distance from p_j^k to p_j^\iota by going along {\tau_j} . By calculating all the commuting distances between location and trajectories in {N_{\rm in}^{t}({r_i}) } and {N_{\rm out}^{t}({r_i}) } according to (1), we can obtain two distance sets D_{\rm in}^{t}({r_i}) and D_{\rm out}^{t}({r_i}) . Subsequently, two normal distributions of {{\cal{N}}_{\rm in}^{t}}({\mu _{r_i}},{\sigma _{r_i}}^2) and {{\cal{N}}_{\rm out}^{t}}({\mu _{r_i}},{\sigma _{r_i}}^2) are employed to fit the data distributions in D_{\rm in}^{t}({r_i}) and D_{\rm out}^{t}({r_i}) , respectively.
The intuition behind this is that a location has higher popularity if there are a greater number of inflow and outflow of crowds, or if the distance between the location and the trajectory is shorter.
4.2.2 Social Relationship
Two essential characteristics of social relationships are acknowledged: the reciprocal recommendation denoted by the number of social friends of dwellers, and the recommending effect of influencers represented by the number of followers. For the first sub-feature, two users (dwellers) are supposed to be close friends if they have followed each other in online social services. Assuming that the corresponding user sets of \Gamma _{\rm in}^t({r_i}) and \Gamma _{\rm out}^t({r_i}) are U_{\rm in}^{t}({r_i}) and U_{\rm out}^{t}({r_i}) , respectively, then the reciprocal recommendation is represented as:
S_{\rm{i}n}^t(r_i)=\sum\limits_{u\in U_{\rm{i}n}^t(r_i)}^{ }|F_s^t(u)|,\ S_{\rm{o}ut}^t(r_i)=\sum\limits_{u\in U_{\rm{o}ut}^t(r_i)}^{ }|F_s^t(u)|, where F_s^{t}(u) is the set of close friends of user u , which only includes those social friends that have trajectory activities in time period t , as the user sets are split by time period for processing.
For the second sub-feature, a user is called an influencer or celebrity if the number of followed users on social networks is greater than the threshold {\varepsilon _{\rm f}} , i.e., | F^{f}(u) | \geqslant {\varepsilon _{\rm f}} . For simplicity, it is supposed that the impact of influencers' recommendations can be seen in all time periods. Therefore, the recommending effect of r_i in all time periods can be defined as the set of V(r_i) = \{ | F^{f}(u_1) |, | F^{f}(u_2) | ,\ldots, | F^{f}(u_m) | \} , \forall j \in [1,m] , | F^{f}(u_1) | \geqslant {\varepsilon _{\rm f}} .
4.2.3 Public Transportation
Public transportation (e.g., bus or metro) is one of the most popular travel modes in large cities due to its cheapness and convenience, and thus it is acknowledged as another essential factor in dweller mobility intentions. In more detail, given an urban region r_i within location l_i and time period t , we follow the extracted sub-features as described in LUCGAN[33], i.e., the set of inflow and outflow of r_i denoted by {\cal{T}} _{\rm in}^t({r_i}) and {\cal{T}} _{\rm out}^t({r_i}) , respectively. Therefore the number of inflow and outflow of public transportation can be represented as:
{{TN}_{\rm in}^{t}({r_i}) } = | {{\cal{T}}_{\rm in}^{t}({r_i}) } |,{{TN}_{\rm out}^{t}({r_i}) } = | {{\cal{T}}_{\rm out}^{t}({r_i}) } |. In addition, the densities of bus stops and metro stations are denoted by D_{\rm b}(r_i) and D_{\rm m}(r_i) , which reflect the numbers of bus stops and metro stations in r_i , respectively.
4.2.4 Similar Facility
The existing facilities of similar categories can adversely affect locations' regional popularity due to homogeneous competition. For example, the decision of opening a Luckin Coffee in a candidate location would entail investigation of similar facilities (e.g., Starbucks and Pacific Coffee) within the same region. To this end, the feature of similar facilities can be denoted as the set of M^{t}(r_i) = \{ y_{l_1}^t(r_i), y_{l_2}^t(r_i), \ldots, y_{l_m}^t(r_i) \} , where y_{l_j}^t(r_i) is the facility popularity of {l_j} over time period t in region r_i , 1 \leqslant j \leqslant m .
To sum up, the multi-dimensional characteristics of location {l_i} (region r_i ) can be represented as a vector {\boldsymbol{X}}_{r_i}^t =\{ {N_{\rm in}^{t}({r_i}) }, \,{N_{\rm out}^{t}({r_i}) } ,\,{\mu _{r_i}}({\rm in},t),\,{\sigma _{r_i}}^2({\rm in},t),\, {\mu _{r_i}}({\rm out},t), {\sigma _{r_i}}^2({\rm out},\,t) ,\;{S}_{\rm in}^{t}(r_i),\; {S}_{\rm out}^{t}(r_i) , \; V(r_i),\, {{TN}_{\rm in}^{t}({r_i}) },\, {{TN}_{\rm out}^{t}({r_i}) }, D_{\rm b}(r_i), D_{\rm m}(r_i),M^{t}(r_i) \} over time period t , where {\mu _{r_i}}({\rm in},t) and {\sigma _{r_i}}^2({\rm in},t) are the mean and square of variance of {{\cal{N}}_{\rm in}^{t}} , respectively. For all time periods T and regional set {\cal{R}} , the feature vectors can be formally aligned by padding 0 to the end if their lengths are inconsistent. Finally, the aggregated characteristics of the three different dimensions, i.e., time period, urban region, and location, are incorporated into tensor {\cal{X}} .
4.3 Location Correlation Graph Construction
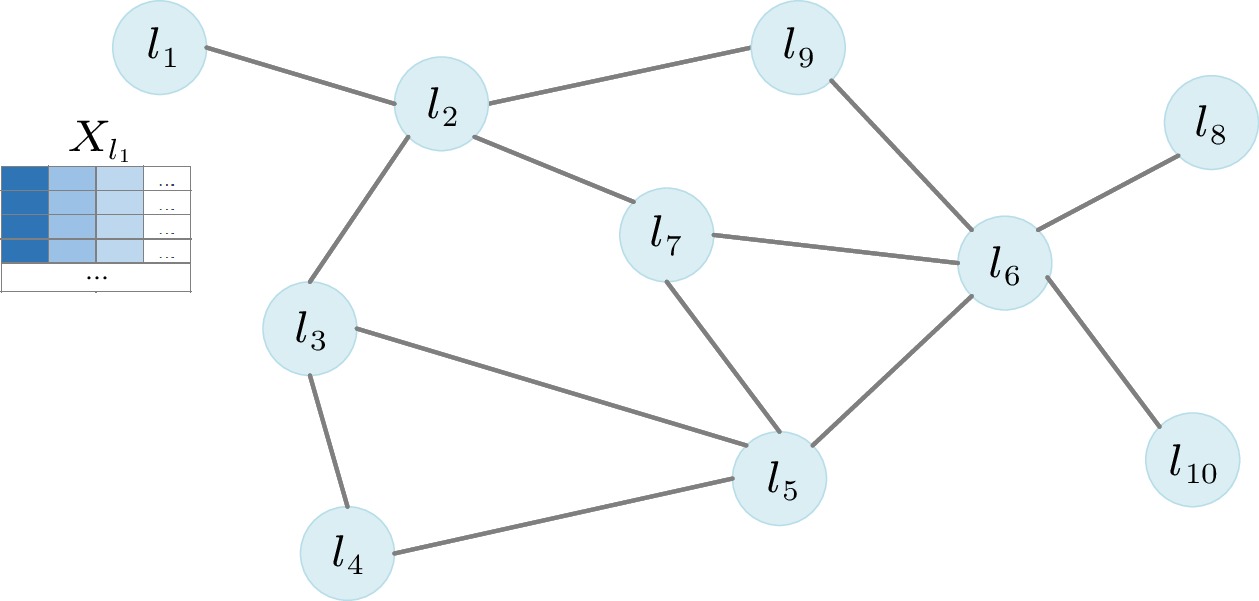
Graph structure Location Correlation Graph (LCG) is introduced to model the real-world correlations among locations. Specifically, as illustrated in Fig.4, locations serve as nodes, and spatial correlations of pair-wise locations are represented as edges, ensuring that both the spatial characteristics and temporal impacts can be captured for the popularity prediction of candidate locations.
Definition 8 (Location Correlation Graph). LCG is an undirected graph that includes locations, regional features, and the corresponding connectivity. It is formally represented as {\cal{G}} = (V,{\cal{X}},\boldsymbol A) , where V is the locations, V = L , |V| = |L| = |R| , and \boldsymbol A denotes the adjacency matrix of {\cal{G}} .
Following a previous study[22], two types of neighbors are designated among the locations (nodes) in {\cal{G}} , i.e., geographical neighbors and semantic neighbors, with the intuition that two corresponded urban regions are geographically close or have similar inflow and outflow patterns. In addition, they are regarded as reflections of local correlations and global correlations among locations.
Specifically, according to the first law of geography that near things are more related than distant things[34], the geographical neighbors are devised to capture local spatial correlations between a location and its adjacent locations. Moreover, for the administrative integrity of urban planning in a city, two locations of l_i and l_j are still considered as geographical neighbors, if the spatial distance between them is no more than a threshold {\varepsilon_g} , i.e., {d_s}({l_i}, {l_j}) \leqslant {\varepsilon_g} .
In addition to local correlations, distant locations can also be correlated through similar contextual features. For example, distant locations in similar functional regions can show similar popularity distributions over time periods. Therefore, we introduce semantic neighbors to denote global correlations among locations with similar inflow and outflow patterns. The Pearson correlation coefficient is utilized to quantify the flow patterns of two regions r_i and r_j . The semantic similarity can be defined as:
\begin{split} {Si}({r_i},{r_j}) = &{\alpha_{\rm s}} P_{\rm s}({Q_{\rm in}^{T}({r_i}) } ,{Q_{\rm in}^{T}({r_j}) } )\;+ \\& (1-{\alpha_{\rm s}}) P_{\rm s}({Q_{\rm out}^{T}({r_i}) },{Q_{\rm out}^{T}({r_j}) }), \end{split} where P_{\rm s} is the function of the Pearson Correlation Coefficient, {\alpha_{\rm s}} is the parameter that controls the weight, Q_{\rm in}^{T}({r_i}) and Q_{\rm out}^{T}({r_i}) denote the count sequences (vectors) of inflow and outflow in r_i over time periods T , respectively.
\begin{split} &{Q_{\rm in}^{T}({r_i}) } = \{ {N_ {\rm in}^{t-T+1}({r_i})},{N_{\rm in}^{t-T+2}({r_i})} ,\ldots,{N_{\rm in}^{t}({r_i})} \}, \\& {Q_{\rm out}^{T}({r_i}) } = \{ {N_ {\rm out}^{t-T+1}({r_i})},{N_{\rm out}^{t-T+2}({r_i})}, \ldots,{N_{\rm out}^{t}({r_i})} \}. \end{split} Therefore, we regard two distant locations as semantic neighbors if their semantic similarity is greater than the threshold {\varepsilon_s} , i.e., {Si}({r_i}, {r_j}) \geqslant {\varepsilon_s} . Subsequently, the adjacency matrix \boldsymbol A of {\cal{G}} is defined as:
{{A}_{ij}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{if}} \; {l_i},{l_j} \; \rm{are} \; \rm{neighbors,}}\\ {0,}&{\rm{otherwise.}} \end{array}} \right. 5. Proposed Model
To facilitate spatio-temporal popularity prediction and candidate location recommendation, we present details of the proposed STGCRN model based on LCG, including four steps: spatial correlation modeling, temporal dependency modeling, popularity prediction and location recommendation, and model training.
5.1 Spatial Correlation Modeling
In the spatial domain, the popularity of adjacent facilities is usually correlated and mutually influenced. For example, when a location has more visits at a time period, the visits of nearby locations tend to be adversely influenced, and the influence of local locations can vary non-linearly. In addition to the local correlation, distant locations can also show similar popularity if they are located in regions with similar functions; for example, large residential regions tend to have lower crowd flows during office hours.
To capture local and global spatial correlations among locations, a contextual convolution (CttConv) block based on LCG is proposed to compute the corresponding coefficients, implemented by the Multi-Head Graph Attention (MGAT) mechanism. The intuition behind CttConv is that graph node v_i \in {\cal{G}} (i.e., location l_i ) can aggregate the multi-dimensional contextual characteristics {{{\boldsymbol{x}}}_{l_j}} of neighboring locations by convolution, where {l_j} \in {N}{({l_i})} , 1 \leqslant j \leqslant |{N}({l_i})| , {N}({l_i}) is the geographical and semantic neighbor set of location {l_i} . Then new implicit features can be generated through characteristic transformation by MGAT. Therefore, the local implicit feature of location l_i at time period t is defined as:
{{\boldsymbol{x}}}_{l_i}^{l,\ t} = \mathop {||}\limits_{k = 1}^K \sigma \left( { \sum\limits_{{l_j} \in {N_l}({l_i})} {{\alpha _{ij}^{k}}{\boldsymbol{W}}_a^{k} {{\boldsymbol{x}}}_{l_j}^{l,\ t - 1}} } \right), where \mathop {||}\nolimits_{k = 1}^K is the concatenation of K implicit sub-features in MGAT, \sigma is a non-linear activation function (e.g., ReLU or Sigmoid), {{\boldsymbol{x}}}_{l_j}^{l,\ t - 1} is the explicit characteristic of l_j over time period t-1 , {N_l}({l_i}) is the geographical neighbor set of l_i , {\boldsymbol{W}}_a^{k} is a learnable weighted matrix shared among locations in the k -th local sub-features, and {\alpha _{ij}^{k}} denotes the proximity score between l_i and l_j in the k -th local sub-features as defined below:
{\alpha _{ij}^{k}} = \frac{{\exp (An({\boldsymbol{W}}_l^{k}{{\boldsymbol{x}}}_{l_i}^{l,\ t - 1},{\boldsymbol{W}}_l^{k}{{\boldsymbol{x}}}_{l_j}^{l,\ t - 1}))}}{{\sum\limits_{{l_k} \in {N_l}({l_i})} {\exp (An({\boldsymbol{W}}_l^{k}{{\boldsymbol{x}}}_{l_i}^{l,\ t - 1},{\boldsymbol{W}}_l^{k}{{\boldsymbol{x}}}_{l_k}^{l,\ t - 1}))} }}, (2) where {\boldsymbol{W}}_l^{k} is also a learnable weighted matrix shared over all edges in {\cal{G}} in the k -th local sub-features, and An is a shared specific attention mechanism, e.g., dot-product.
Meanwhile, the global implicit characteristic of location l_i over a time period t is similarly calculated as:
{{\boldsymbol{x}}}_{l_i}^{g,\ t} = \mathop {||}\limits_{k = 1}^K \sigma \left( { \sum\limits_{{l_j} \in {N_g}({l_i})} {{\beta _{ij}^{k}}{\boldsymbol{W}}_s^{k}{{\boldsymbol{x}}}_{l_j}^{g,\ t - 1}} } \right), where {N_g}({l_i}) is the semantic neighbor set of l_i , {\boldsymbol{W}}_s^{k} is a learnable weighted matrix shared over all locations in the k -th global sub-features, and {\beta _{ij}^{k}} denotes the proximity score between l_i and l_j in the k -th global sub-features as defined below:
{\beta _{ij}^{k}} = \frac{{\exp (An({\boldsymbol{W}}_g^{k}{\boldsymbol{x}}_{l_i}^{g,\ t - 1},{\boldsymbol{W}}_g^{k}{{\boldsymbol{x}}}_{l_j}^{g,\ t - 1}))}}{{\sum\limits_{{l_k} \in {N_g}({l_i})} {\exp (An({\boldsymbol{W}}_g^{k} {{\boldsymbol{x}}}_{l_i}^{g,\ t - 1},{\boldsymbol{W}}_g^{k}{{\boldsymbol{x}}}_{l_k}^{g,\ t - 1}))} }}, (3) where {\boldsymbol{W}}_g^{k} is a learnable weighted matrix shared over all edges in {\cal{G}} in the k -th global sub-features.
5.2 Temporal Dependency Modeling
In the temporal domain, dependencies consistently exist inside locations themselves. Therefore, we employ LSTM, an effective variant implementation of RNN, to extract the sequential hidden characteristics and then model the corresponding temporal dependencies. Specifically, let the input characteristic sequences of l_i be defined as {\boldsymbol{X}}_{l_i} = \{{{{\boldsymbol{x}}}_{l_i}^{t - T + 1}},{{{\boldsymbol{x}}}_{l_i}^{t - T + 2}},\ldots, {{{\boldsymbol{x}}}_{l_i}^t}\} in previous T steps, and let the implicit status of l_i at time steps t-1 and t be denoted as {{\boldsymbol{h}}}_{l_i}^{t - 1} and {{\boldsymbol{h}}}_{l_i}^{t} , respectively. Then the temporal dependency between {{\boldsymbol{h}}}_{l_i}^{t - 1} and {{\boldsymbol{h}}}_{l_i}^{t} can be represented as follows:
\begin{split} &{\boldsymbol{f}}_{l_i}^t = \sigma ({{\boldsymbol{W}}_{\rm f}}[{{\boldsymbol{h}}}_{l_i}^{t - 1},{{\boldsymbol{x}}}_{l_i}^t] + {{\boldsymbol{b}}_{\rm f}}), \\&{\boldsymbol{z}}_{l_i}^t = \sigma ({{\boldsymbol{W}}_z}[{{\boldsymbol{h}}}_{l_i}^{t - 1} \oplus {{\boldsymbol{x}}}_{l_i}^t] + {{\boldsymbol{b}}_z}), \\&{\tilde{\boldsymbol{C}}}_{l_i}^{t} = tanh ({{\boldsymbol{W}}_C}[{{\boldsymbol{h}}}_{l_i}^{t - 1} \oplus {{\boldsymbol{x}}}_{l_i}^t] + {{\boldsymbol{b}}_C}), \\&{\boldsymbol{C}}_{l_i}^t = {\boldsymbol{f}}_{l_i}^t \odot {{\boldsymbol{C}}_{l_i}^{t - 1}} + {{\boldsymbol{z}}_t} \odot {{\tilde{\boldsymbol{C}}}_{l_i}^{t}}, \\&{\boldsymbol{o}}_{l_i}^t = \sigma ({{\boldsymbol{W}}_o}[{{\boldsymbol{h}}}_{l_i}^{t - 1} \oplus {{\boldsymbol{x}}}_{l_i}^t] + {{\boldsymbol{b}}_o}), \\&{{\boldsymbol{h}}}_{l_i}^t = {\boldsymbol{o}}_{l_i}^t \odot tanh {\boldsymbol{C}}_{l_i}^t, \end{split} where {{\boldsymbol{f}}_{l_i}^t} is the forget gate in LSTM, {{\boldsymbol{z}}_{l_i}^t} is the input gate, {{\tilde{\boldsymbol{C}}}_{l_i}^{t}} denotes the cell state, {{\boldsymbol{C}}_{l_i}^t} denotes the cell update, {{\boldsymbol{o}}_{l_i}^t} is the output gate, {{\boldsymbol{W}}_{\rm f}} , {{\boldsymbol{W}}_z} , {{\boldsymbol{W}}_C} , {{\boldsymbol{W}}_o} , {{\boldsymbol{b}}_{\rm f}} , {{\boldsymbol{b}}_z} , {{\boldsymbol{b}}_C} , and {{\boldsymbol{b}}_o} are learnable parameters, \oplus is the concatenation operation, tanh is the activation function, tanh (z) = {{({{\rm{e}}^z} - {{\rm{e}}^{ - z}})} / {({{\rm{e}}^z} + {{\rm{e}}^{ - z}})}} , and \odot is the hadamard product. In addition, the hidden state {{\boldsymbol{h}}}_{l_i}^{t} can be directly used to predict the popularity of the next consecutive T_{\rm f} periods:
(\hat{y}_{l_i}^{t+1},\hat{y}_{l_i}^{t+2},\ldots,\hat{y}_{l_i}^{t+T_{\rm f}}) = \sigma({\boldsymbol{W}}_o {{\boldsymbol{h}}}_{l_i}^{t}), where {\boldsymbol{W}}_o \in {\mathbb{R}}^{|{{\boldsymbol{h}}}_{l_i}^{t}|\times T_{\rm f}} .
5.3 Popularity Prediction and Location Recommendation
The historical popularity (check-ins) of existing facilities is an exceptional input characteristic that can help to improve the accuracy of the future popularity prediction for candidate locations. However, due to data privacy concerns, only a small percentage of valid historical check-in information is collected through online social services.
To better employ the information hidden in these few existing facilities, we propose the approximation module for missing popularity from both the spatial and temporal domains, consisting of three blocks: the spatial graph convolution block, the temporal LSTM block, and the fusion block. Moreover, we learn the probability distribution of location popularity, i.e., {{{\boldsymbol{y}}}_{l_i}^{v}} = P({y}_{l_i}) , rather than approximate a scalar popularity {y}_{l_i} , for better information preservation. For historical popularity {\cal{Y}} _{{L_l}} , the one-hot encoding is employed to discretize {\cal{Y}} _{{L_l}} to vectors. Finally, the approximated popularity distributions are concatenated with both local and global spatial characteristics, and are subsequently fed into the LSTM blocks to obtain the ultimate popularity for the recommendation.
5.3.1 Spatial Approximation
Similar to CttConv, we propose the prediction convolution (PrdConv) block also implemented by MGAT, to estimate location popularity from both the local and global spatial domains. Unlike CttConv, the approximated popularity is only the aggregated historical popularity of existing location facilities. Therefore, PrdConv can improve node connectivity for more sufficient propagation of historical popularity, which alleviates the data scarcity problem. The aggregated vector representations can be preserved for further processing without extra activation functions. Specifically, in a time period t , the local spatial popularity distribution {{{\boldsymbol{y}}}}_{l_i}^{{\rm sdl},\ t} of each location {l_i} \in {L_u} is defined as:
{{{\boldsymbol{y}}}}_{l_i}^{{\rm sdl},\ t} = \frac{1}{K}\sum\limits_{k = 1}^K { \sum\limits_{j \in {N_l}({l_i})} {{\alpha _{ij}^{k}{{\boldsymbol{y}}}_{l_i}^{t}}} }, and the global spatial popularity {{{\boldsymbol{y}}}}_{l_i}^{{\rm sdg},\ t} of each location {l_i} \in {L_u} is defined in a similar way:
{{{\boldsymbol{y}}}}_{l_i}^{{\rm sdg},\ t} = \frac{1}{K}\sum\limits_{k = 1}^K { \sum\limits_{j \in {N_g}({l_i})} {{\beta _{ij}^{k}{{\boldsymbol{y}}}_{l_i}^{t}}} }, where \alpha _{ij}^{k} and \beta _{ij}^{k} are the local and global proximity scores between {l_i} and {l_j} computed through MGAT in (2) and (3), respectively.
5.3.2 Temporal Approximation
In the temporal domain, we reuse the outputs of the LSTM block to approximate the missing popularity distributions. Unlike the implementation of final popularity prediction, the missing popularity estimation adopts a different Softmax function. Specifically, suppose that the hidden state obtained from LSTM is {{\boldsymbol{h}}}_{l_i}^{t-1} in previous time period t-1 , then the approximated missing popularity distribution at t is defined as:
{\boldsymbol{y}}_{l_i}^{{\rm td},\ t} = {\rm Softmax}({{\boldsymbol{W}}_{td}}{{\boldsymbol{h}}}_{l_i}^{t-1}), where {\boldsymbol{W}}_{td} is a learnable weighted matrix shared by all hidden states. In addition, this step involves no additional computation of LSTM, and all the vector elements in {{\boldsymbol{y}}}_{l_i}^{{\rm td},\ t} can be normalized and their sum is 1.
5.3.3 Distribution Fusion
According to previous studies[18, 24], the ultimate popularity estimation weighs more on approximation and has less uncertainty in recommendation model. Therefore, an entropy-based mechanism is employed to fuse the spatio-temporal distributions rather than average them directly, and subsequently the approximation results with smaller entropy are the outcome. Given an approximated popularity distribution {{\boldsymbol{y}}}_{l_i}^{t} , the entropy is defined as:
H({{\boldsymbol{y}}}_{l_i}^t) = - \sum\limits_{j = 1}^p {{{\boldsymbol{y}}}_{l_i}^t(j) \log {{\boldsymbol{y}}}_{l_i}^t(j)}, where {{\boldsymbol{y}}}_{l_i}^t(j) denotes the j-th dimension of {{\boldsymbol{y}}}_{l_i}^t , {{\boldsymbol{y}}}_{l_i}^t \in {\mathbb{R}}^p . The spatio-temporal distribution fusion is defined in (4).
\begin{split} {{\boldsymbol{y}}}_{l_i}^{f,\ t} =& \Big(\exp ( - H({{\boldsymbol{y}}}_{l_i}^{{\rm sdl},\ t})){{\boldsymbol{y}}}_{l_i}^{{\rm sdl},\ t} + \exp ( - H({{\boldsymbol{y}}}_{l_i}^{{\rm sdg},\ t})){{\boldsymbol{y}}}_{l_i}^{{\rm sdg},\ t} +\\&\, \exp ( - H({{\boldsymbol{y}}}_{l_i}^{{\rm td},\ t})){{\boldsymbol{y}}}_{l_i}^{{\rm td},\ t}\Big)\Big/ \Big(\exp ( - H({{\boldsymbol{y}}}_{l_i}^{{\rm sdl},\ t})) +\\&\, \exp ( - H({{\boldsymbol{y}}}_{l_i}^{{\rm sdg},\ t})) + \exp ( - H({{\boldsymbol{y}}}_{l_i}^{{\rm td},\ t}))\Big). \\[-1pt]\end{split} (4) 5.3.4 Popularity Prediction and Location Recommendation
The approximated popularity distribution is combined with the outputs of CttConv, to obtain the overall hidden characteristics {{\boldsymbol{x}}}_{l_i}^{t} for each location l \in L at time period t , i.e., {{\boldsymbol{x}}} _{l_i}^{t} = {{\boldsymbol{x}}}_{l_i}^{l,t} \oplus {{\boldsymbol{x}}}_{l_i}^{g,\ t} \oplus {{\boldsymbol{y}}}_{l_i}^{f,t} . Next, the hidden location representations are fed into the LSTM module to generate ultimate popularity distributions. Subsequently, a multi-layer perceptron (MLP) module is employed to scalarize the generated distributions, to obtain the final popularity prediction results for each candidate location.
In the recommendation process, we can sort the candidate location set from the spatial dimension or the temporal dimension according to the predicted popularity, and then generate a series of well-ranked candidate location lists for top- k incremental recommendation. For instance, they can predict the top-10 popular candidate locations in an upcoming month or popularity trends of a particular candidate location in the next six months.
5.4 Model Training
STGCRN is a typical semi-supervised model based on existing location facilities with historical popularity, and therefore a number of semi-supervised learning paradigms can be adopted in the model training. In missing popularity approximation, the cross entropy (CE) loss is introduced to minimize the errors between actual popularity ( {{\boldsymbol{y}}} _{l_i}^t ) and estimated popularity distributions, i.e., {{\boldsymbol{y}}} _{l_i}^{{\rm sdl},\ t} , {{\boldsymbol{y}}}_{l_i}^{{\rm sdg},\ t} , and {{\boldsymbol{y}}}_{l_i}^{{\rm td},\ t} . The three loss functions are separately defined as follows:
\begin{split} &{O_{\rm sdl}} = - \dfrac{1}{{|{L_{\rm l}}||{T_{\rm h}}|}}\sum\limits_{i = 1}^{|{L_{\rm l}}|} {} \sum\limits_{j = 1}^{|{T_{\rm h}}|} {{{\boldsymbol{y}}}_{l_i}^{t - {T_{\rm h}} + j}\log {{\boldsymbol{y}}}_{l_i}^{{\rm sdl},\ t - {T_{\rm h}} + j}}, \\& {O_{\rm sdg}} = - \dfrac{1}{{|{L_{\rm l}}||{T_{\rm h}}|}}\sum\limits_{i = 1}^{|{L_{\rm l}}|} {} \sum\limits_{j = 1}^{|{T_{\rm h}}|} {{{\boldsymbol{y}}}_{l_i}^{t - {T_{\rm h}} + j}\log {{\boldsymbol{y}}}_{l_i}^{{\rm sdg},\ t - {T_{\rm h}} + j}}, \\& {O_{\rm td}} = - \dfrac{1}{{|{L_{\rm l}}||{T_{\rm h}}|}}\sum\limits_{i = 1}^{|{L_{\rm l}}|} {} \sum\limits_{j = 1}^{|{T_{\rm h}}|} {{{\boldsymbol{y}}}_{l_i}^{t - {T_{\rm h}} + j}\log {{\boldsymbol{y}}}_{l_i}^{{\rm td},\ t - {T_{\rm h}} + j}}. \end{split} In the process of final popularity prediction, we aim to minimize the mean square error (MSE) between the predicted popularity ( \tilde{\boldsymbol y}_{l_i}^{t} ) and actual popularity, therefore the loss function is defined as:
O_{\rm p} = \frac{1}{{|{L_{\rm l}}||{T_{\rm f}}|}}\sum\limits_{i = 1}^{|{L_{\rm l}}|} {} \sum\limits_{j = 1}^{|{T_{\rm f}}|} {{{(\tilde{y}_{l_i}^{t + j} - y_{l_i}^{t + j})}^2}}. By acknowledging the CE loss and MSE loss, the learning objective of STGCRN is to minimize the following function on the basis of comprehensive analysis of both:
O = {\alpha _{\rm l}}({O_{\rm sdl}} + {O_{\rm sdg}} + {O_{\rm td}}) +(1 - {\alpha _{\rm l}} ) {O_{\rm p}}, where {\alpha _{\rm l}} is the parameter that controls the weight of two losses.
6. Experimental Study
Extensive experiments are conducted in this section. First, we introduce the experimental setup, including dataset description and experimental implementation. Next, the baselines and evaluation metrics are established. The effectiveness and stability of the proposed model compared with baselines are finally reported.
6.1 Experimental Setup
6.1.1 Datasets
This paper does not focus on discussing the factors that affect the determination of candidate locations. Instead, it uses the road intersections as candidate locations for the input of the proposed approach. We choose the Beijing central district and the New York Manhattan district as the geographical areas for location recommendation by extracting the structures of the road network from Openstreet[35] and initializing the candidate location set, and then combining them with the corresponding location-based social datasets, i.e., spatio-temporal trajectories, social networks, and POI check-ins. As a result, two real datasets of Beijing Central District (BJCD) and New York Manhattan District (NYMD) are established to conduct the entire experiments, as described in detail in Table 2. Meanwhile, we predict location popularity in future successive time periods according to the timestamps of both trajectory stay points and POI check-ins. Specifically, the datasets are collected from February 2014 to January 2015, divided into 12 consecutive months and 52 weeks.
Table 2. Summary of Dataset StatisticsDataset Number of
Road
IntersectionsNumber of
Road
SegmentsNumber of
Candidate
LocationsNumber of
Customers/
TrajectoriesNumber of
Social
Network NodesNumber of
Social
RelationshipsNumber of
POI
Check-insBJCD 136903 176384 110102 13936 709671 3530549 3547711 NYMD 5310 6891 5008 3381 71817 1414519 836482 1) BJCD. The first dataset contains
13936 customers (urban dwellers) within three offline-online location-based social characteristic sets, i.e., offline spatio-temporal trajectories obtained from traveling records of Beijing taxis, online social friend relationships crawled from Sina Weibo1 , and POI check-in records also crawled from Sina Weibo.2) NYMD. The second dataset contains
3381 customers, where social friend relationships and POI check-ins are crawled from Twitter2 and Instagram3 , and trajectories are extracted from traveling records of taxis and shared bikes in the Manhattan district. However, the original trajectories only include the information (e.g., positions and timestamps) of departures and arrivals, which prevents us from capturing the whole process of customer travels. Since the road network structure in Manhattan is straight and regular, we employ the road route that has the shortest spatial distance from departure to arrival as the complete trajectory.A series of existing facilities datasets is also collected for model training, and the corresponding statistics are reported in Table 3. In BJCD, we choose three types of service facilities from the open LBS platform of AutoNavi
4 : Baby Service Place (BSP), China Unicom Service Hall (CUSH), and fast Vehicle Charging Station (VCS). In NYMD, three types of fast-moving consuming facilities, i.e., Starbucks (SBS), 7-Eleven (7-11), and McDonald's (MDS), are extracted from the open platform of Google Maps5 .Table 3. Statistics of Existing FacilitiesFacility Number of
StoresNumber of
Check-insNumber of
Average Check-insBSP 416 387025 930 CUSH 585 237123 405 VCS 729 319957 439 SBS 203 104681 516 7-11 118 19548 166 MDS 84 39069 465 6.1.2 Implementation
All models are implemented with Python 3.6.0 and Pytorch 1.6.0. The datasets of trajectory and POI check-in are divided into 12 parts and 52 parts, according to month and week, respectively. We choose T_{\rm h} = 9 and T_{\rm f} = 3 for monthly prediction, and set T_{\rm h} = 28 and T_{\rm f} = 6 for weekly prediction. We set {\varepsilon_{\rm f}} =
1000 , {\varepsilon_g} =2000 , {\varepsilon_s} = 0.4, and {\alpha_s} = 0.5 for the thresholds and weight, respectively. The number of layers of CxtConv and PrdConv are all set to 2, and the number of latent characteristics is K = 6 in MGAT. The dot-product attention mechanism is employed in this paper. The activation function is set to Parametric ReLU (PReLU, \alpha = 0.2) in CxtConv and PrdConv, and Sigmoid in the other layers, e.g., MLP. We adopt the “6/2/2” principle to utilize the datasets, where the first 60% are taken as the training set, the following 20% for validation, and the rest is the test set. In each dataset, 70% POI facilities are marked as unlabeled. We set the batch size as 32 for training, and the Adam Optimizer is adopted with the fixed learning rate of \alpha = 0.001 and \beta s = (0.9, 0.999). The recommendation number set of candidate locations is k \in \{20,30,50,80\} , where k = 30 is set as the default.6.2 Baselines
We compare the performance of proposed STGCRN with a range of competitive methods and two variants of STGCRN. Although some models[19, 24] are not initially designed for popularity prediction or location recommendation of urban facilities, we extend them for contrast due to the similarity of their predictive theory.
● RK. Regression Kriging[36] is a hybrid approach of Generalized Linear Model and Ordinary Kriging, where location popularity is calculated based on the weighted averages of geographical neighbors in LCG. This study extends RK to multi-step popularity prediction in the temporal domain by concatenating concessive predicted popularity in each time step.
● MF-STN. Matrix Factorization for Spatio-Temporal Neural Networks (MF-STN)[17] decomposes the region-specific parameters into learnable matrices to model latent functions and correlations among regions for popularity prediction in the spatial and temporal domains. The region partition is implemented by LCG as explained in Definition 8.
● L-CoT. Co-Training[19] is a semi-supervised learning framework based on two separated classifiers, including a spatial classifier based on an artificial neural network and a temporal classifier based on a linear-chain conditional random field. We extend it to the popularity prediction of L-CoT (Location-CoT), where the monitor station is taken as the location.
● L-SHARE. Semi-Supervised Hierarchical Recurrent Graph Neural Network[24] is a state-of-the-art method devised for city-wide parking availability prediction. A hierarchical graph convolution module and a gated recurrent unit module are proposed to model the spatial and temporal correlations between parking lots. We extend it to L-SHARE, where the parking lot is regarded as the location.
● API. Affinity-Based Popularity Inference[5] is a state-of-the-art graph-based semi-supervised learning method. It employs a set of location affinity functions to model the affinities (similarities) between locations. Then, based on the intuition that nearby locations with high affinity scores may have similar popularity distributions, the Gaussian random field is employed to evaluate the temporal popularity of candidate locations.
● STGCRN-GA. STGCRN-GA is an elementary version of STGCRN, where both the global CttConv (MGAT) and the missing popularity approximation module are removed.
● STGCRN-A. STGCRN-A is another essential variant of our proposed model, but excludes the missing popularity approximation module, where the hidden states obtained from LSTM are directly fed into MLP to predict the final popularity.
● STGCRN. STGCRN is the final approach, where the spatio-temporal popularity is evaluated as described in Section 5.
6.3 Evaluation Metrics
To evaluate the effectiveness of popularity prediction, two typical metrics are designed: accuracy (Acc) and root mean square error (RMSE). Suppose that the predicted popularity and the ground-truth popularity of l_i \in L_u in time period t_j \in T_{\rm f} are \tilde{y}_{l_i}^{t} and y_{l_i}^t , respectively, then the accuracy can be defined as:
{{{Acc}} = }\frac{{\sum\nolimits_{{l_i} \in {L_u} } \sum\nolimits_{{t_j} \in {T_{\rm f}} } {hit(\tilde{y}_{l_i}^{t_j},y_{l_i}^{t_j})} }}{{|T_{\rm f}| \times |{L_u}|}}, where hit() is the hit function, and {hit(\tilde{y}_{l_i}^{t},y_{l_i}^{t})} = 1, if \tilde{y}_{l_i}^{t}-\varepsilon_a \leqslant y_{l_i}^{t} \leqslant \tilde{y}_{l_i}^{t}+\varepsilon_a , otherwise {hit(\tilde{y}_{l_i}^{t},y_{l_i}^{t})} = 0. The parameter \varepsilon_a controls the evaluation strictness by varying the granularity of the ground-truth popularity. Specifically, a lower \varepsilon_a value implies a stricter evaluation that the accuracy tends to be lower for different approaches, and vice versa. To balance the evaluation strictness and accuracy, we set \varepsilon_a to 5. In addition, we use RMSE to measure the variances between the predicted and the ground-truth popularity in spatio-temporal domains, where a lower RMSE value refers to better evaluation performance. Specifically, RMSE is defined as:
{{RMSE}} = \sqrt {\frac{{\displaystyle\sum\limits_{{l_i} \in {L_u}} \displaystyle\sum\limits_{{t_j} \in {T_{\rm f}} } {{{(\tilde{y}_{l_i}^{t_j} - y_{l_i}^{t_j})}^2}} }}{{|T_{\rm f} | \times |{L_u}|}}}. To measure the ranking quality of the recommended top- k candidate locations, we employ the normalized discounted cumulative gain (NDCG) metric that is frequently used in the performance evaluation of information retrieval systems[1]. Given the two top- k descending-ordered lists of the estimated and the ground-truth popularity: \tilde{R} and R , NDCG@ k is defined as:
{NDCG}@k = \frac{{{DCG}@k}}{{{IDCG}@k}} = \frac{{\displaystyle\sum\limits_{i = 1}^k {\frac{{{2^{\tilde{r}({l_i})}} - 1}}{{{{\log }}(i + 1)}}} }}{{\displaystyle\sum\limits_{i = 1}^k {\frac{{{2^{r({l_i})}} - 1}}{{{{\log }}(i + 1)}}} }}, where IDCG@ k is the maximum possible DCG@ k for the ground-truth set of the ranking list, and \tilde{r}({l_i}) and {r}({l_i}) denote the relative scores of l_i at position i in \tilde{R} and R , respectively. Taking DCG@ k as an example, we have r({l_i}) = ({{|{L_u}| - p({l_i}) + 1}})/{{|{L_u}|}} , r({l_i}) \in [0,1] , and p({l_i}) indicates the relative position number from left to right in R . In addition, NDCG @k \in (0,1] , and a greater value of NDCG implies a more precise recommendation result.
6.4 Evaluation Results
6.4.1 Effectiveness Evaluation
The weekly and monthly experimental results of Acc and RMSE for six specific facilities in BJCD and NYMD are shown in Table 4 and Table 5, respectively, and the results of the proposed STGCRN model (including its two variants) are bolded in this subsection. As expected, we can see that the proposed STGCRN model (including its two variants) significantly outperforms all competitors under all conditions. Specifically, STGCRN achieves, on average, (21.18%, 21.71%, 21.73%) and (48.68%, 45.56%, 49.17%) improvements beyond the state-of-the-art API framework on Acc and RMSE in BJCD for BSP, CUSH, and VCS, respectively. Similarly, the averaged improvements of Acc and RMSE are (25.64%, 16.58%, 17.54%) and (44.57%, 31.57%, 36.39%) in SBS, 7-11, and MDS, respectively. This is because STGCRN not only considers both the spatio-temporal activity trajectory and the social friend relationship of urban dwellers, but also captures the spatial correlation of locations through contextual graph convolutional module and the temporal dependency through the LSTM module, which better resolves the intractable problems of customer effect, spatial correlation, and temporal dependency in popularity prediction.
Table 4. Effectiveness Evaluation in BJCD w.r.t. k = 30Method BSP CUSH VCS Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.17 63.10 0.16 71.67 0.15 68.77 0.13 78.67 0.14 72.34 0.15 76.07 MF-STN 0.25 52.48 0.19 58.24 0.26 53.49 0.20 63.51 0.27 56.52 0.22 60.33 L-CoT 0.28 37.38 0.24 44.71 0.30 40.70 0.22 51.08 0.25 31.11 0.25 49.15 L-SHARE 0.39 28.55 0.36 36.37 0.39 29.14 0.29 40.22 0.35 32.89 0.32 43.90 API 0.41 25.79 0.35 22.32 0.38 28.12 0.32 28.88 0.38 27.36 0.35 29.16 STGCRN-GA 0.42 20.09 0.35 21.65 0.40 22.60 0.33 28.61 0.40 23.92 0.37 28.39 STGCRN-A 0.44 14.41 0.38 19.06 0.42 17.31 0.35 24.70 0.43 18.55 0.38 22.14 STGCRN 0.49 8.92 0.43 15.19 0.45 11.66 0.40 19.41 0.48 10.13 0.41 18.85 Table 5. Effectiveness Evaluation in NYMD w.r.t. k = 30Method SBS 7-11 MDS Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.21 67.04 0.18 77.13 0.19 63.99 0.19 85.20 0.23 69.97 0.20 79.19 MF-STN 0.31 54.83 0.23 63.75 0.30 53.10 0.21 66.58 0.28 55.18 0.24 64.77 L-CoT 0.33 41.98 0.24 49.28 0.34 39.84 0.27 48.19 0.31 43.72 0.28 59.11 L-SHARE 0.37 30.67 0.28 40.39 0.35 29.04 0.30 44.81 0.37 28.30 0.29 42.74 API 0.39 23.10 0.33 25.61 0.38 25.22 0.35 29.03 0.38 24.22 0.36 32.66 STGCRN-GA 0.41 20.33 0.36 22.69 0.38 24.77 0.37 25.82 0.41 22.14 0.38 28.79 STGCRN-A 0.42 17.84 0.38 19.01 0.40 20.37 0.38 24.20 0.43 18.65 0.39 25.94 STGCRN 0.46 12.71 0.44 14.30 0.43 16.47 0.42 20.77 0.45 15.01 0.42 21.31 However, most competitors purely learn popularity from urban macro characteristics, such as traffic flow, facility check-in, or facility category, rendering suboptimal results. Although L-SHARE and API consider temporal characteristics and employ a graph-based structure to model the correlations among locations, they fail to capture multi-dimensional features of dwellers, and predict missing popularity in terms of existing check-ins. Therefore, all the above results demonstrate the effectiveness of the missing popularity approximation, hierarchical graph convolution, and recurrent neural network of STGCRN.
In addition, it is observed that the performance during the weekly period is generally superior to that during the monthly period. We think such results are likely due to the far more partitioned time slots in weekly periods, which facilitates a better model learning process as the characteristics accumulated in each month is lower than that in each week. Therefore, the popularity across weeks tend to be closer to each other, making the corresponding prediction relatively easier.
We proceed to report the effectiveness of all approaches by varying parameter k , which enables the detailed demonstration of the performance of two typical facilities out of the six ones in terms of BSP and SBS. According to the results in Table 6 and Table 7, the proposed model still beats all competitors under different k values, which corresponds to the results of a fixed k reported in Table 4 and Table 5.
Table 6. Effectiveness Evaluation Using BSP in BJCD w.r.t. Varied kMethod k = 20 k = 30 k = 50 k = 80 Week Month Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.19 60.46 0.20 61.82 0.17 63.10 0.16 71.67 0.14 82.21 0.13 85.63 0.11 89.77 0.09 107.25 MF-STN 0.24 49.86 0.22 47.75 0.25 52.48 0.19 58.24 0.21 65.76 0.18 69.55 0.19 72.10 0.15 84.52 L-CoT 0.27 38.90 0.25 45.24 0.28 37.38 0.24 44.71 0.27 51.60 0.23 56.30 0.24 61.38 0.21 69.71 L-SHARE 0.41 26.17 0.34 37.72 0.39 28.55 0.36 36.37 0.35 37.23 0.32 45.58 0.29 53.14 0.27 58.44 API 0.45 22.33 0.40 25.41 0.41 25.79 0.35 22.32 0.37 21.86 0.32 40.41 0.34 45.02 0.29 57.19 STGCRN-GA 0.48 18.93 0.45 19.17 0.42 20.09 0.35 21.65 0.40 16.19 0.34 26.09 0.37 30.50 0.32 43.63 STGCRN-A 0.50 15.35 0.47 16.96 0.44 14.41 0.38 19.06 0.41 11.78 0.37 23.13 0.38 24.41 0.35 34.11 STGCRN 0.55 8.19 0.53 10.70 0.49 8.92 0.43 15.19 0.46 10.04 0.40 19.96 0.43 15.14 0.39 22.67 Table 7. Effectiveness Evaluation Using SBS in NYMD w.r.t. Varied kMethod k = 20 k = 30 k = 50 k = 80 Week Month Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.25 60.31 0.22 65.28 0.21 67.04 0.18 77.13 0.20 70.07 0.15 84.93 0.15 89.60 0.11 103.99 MF-STN 0.34 50.49 0.29 58.50 0.31 54.83 0.23 63.75 0.27 64.60 0.19 79.64 0.22 76.82 0.14 91.02 L-CoT 0.35 48.87 0.33 40.04 0.33 41.98 0.24 49.28 0.31 56.03 0.23 73.90 0.29 55.88 0.20 77.08 L-SHARE 0.40 23.79 0.36 32.21 0.37 30.67 0.28 40.39 0.34 47.41 0.24 62.23 0.32 50.25 0.22 70.89 API 0.44 18.32 0.41 22.12 0.39 23.10 0.33 25.61 0.36 45.45 0.29 48.51 0.35 47.77 0.27 54.01 STGCRN-GA 0.45 15.03 0.42 18.20 0.41 20.33 0.36 22.69 0.39 35.21 0.32 40.54 0.37 36.10 0.30 43.33 STGCRN-A 0.47 11.77 0.44 14.97 0.42 17.84 0.38 19.01 0.40 33.95 0.35 36.09 0.38 32.47 0.34 37.57 STGCRN 0.53 8.17 0.50 9.71 0.46 12.71 0.44 14.30 0.43 22.10 0.39 27.15 0.42 23.36 0.37 31.44 Specifically, STGCRN achieves, on average, (27.36%, 21.18%, 24.66%, 38.48%) and (60.61%, 48.68%, 52.34%, 63.37%) improvements beyond the state-of-the-art API approach on Acc and RMSE in BSP for k = 20, 30, 50, and 80, respectively. Similarly, the averaged improvements of Acc and RMSE are (21.20%, 25.64%, 26.96%, 28.52%) and (55.75%, 44.57%, 47.15%, 46.44%) in SBS. The results show that the performance of BSP is superior to that of SBS. It is due to the fact that the dataset of BSP is well-collected, where the numbers of spatio-temporal trajectories, social friend relationships, BSP facilities, and the corresponding check-ins are larger in BJCD. Therefore, the models are more prone to learn the latent characteristics and complex parameters. Besides, it consistently reveals the advantage of incorporating multi-dimensional characteristics of dwellers for popularity prediction and location recommendation.
On the contrary, the overall effectiveness decreases successively with the increase of k in all cases, and these approaches achieve the best performance when setting k to 20. We think such understandable results are due to more comparisons between the pairs of recommended locations and ground-truth locations driven by a larger k value, which leads to the rise of result uncertainty. For instance, a facility located in a prosperous district of an urban center will gain more check-ins than one in an underdeveloped district due to huge visitor flows with great consumption. Thus, the prediction performance becomes more accurate due to the abundant characteristics of this location. In contrast, the performance of popularity prediction in remote locations has a modest reduction since they lack adequate explicit features. However, as k increases, our proposed STGCRN still has the best performance, and its performance decline is not significant compared with the baselines.
Furthermore, we have implemented two variants of STGCRN, i.e., STGCRN-GA and STGCRN-A, to evaluate the module improvements. As expected, the overall performance of STGCRN-GA and STGCRN-A generally outperforms the five baselines. This is because our proposed variants significantly consider and incorporate the spatio-temporal characteristics of urban dwellers and locations. There is a successive effectiveness improvement by comparing STGCRN with its two variants. For instance, by adding the MGAT block, STGCRN-A achieves, on average, 5.77% greater Acc and 20.29% lower RMSE compared with STGCRN-GA in BJCD when k = 30. By further adding the missing popularity approximation module, STGCRN achieves, on average, 10.91% greater Acc and 28.67% lower RMSE compared with STGCRN-A. Improvements are also consistent under other conditions, such as in NYMD and with varied k . All above results demonstrate the promising effectiveness of global spatial correlation capturing and missing popularity approximating.
6.4.2 Stability Evaluation
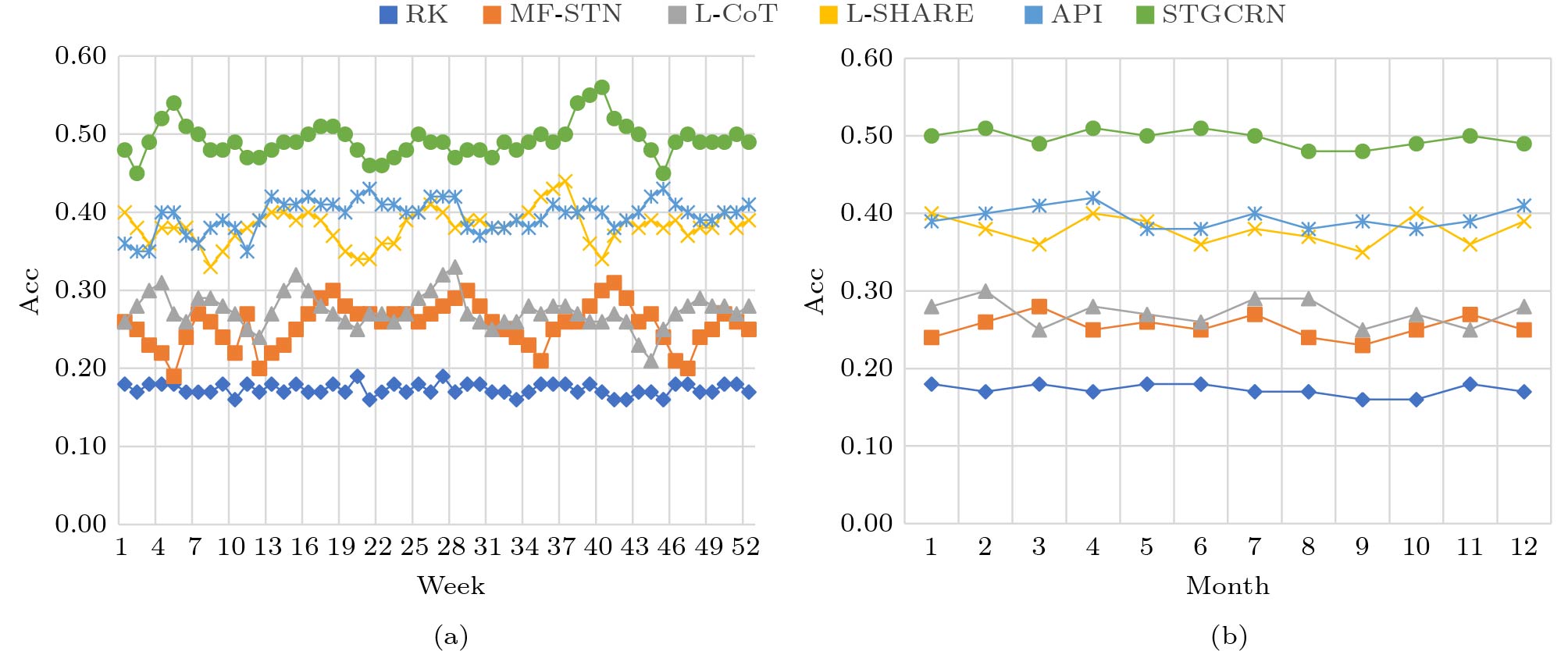
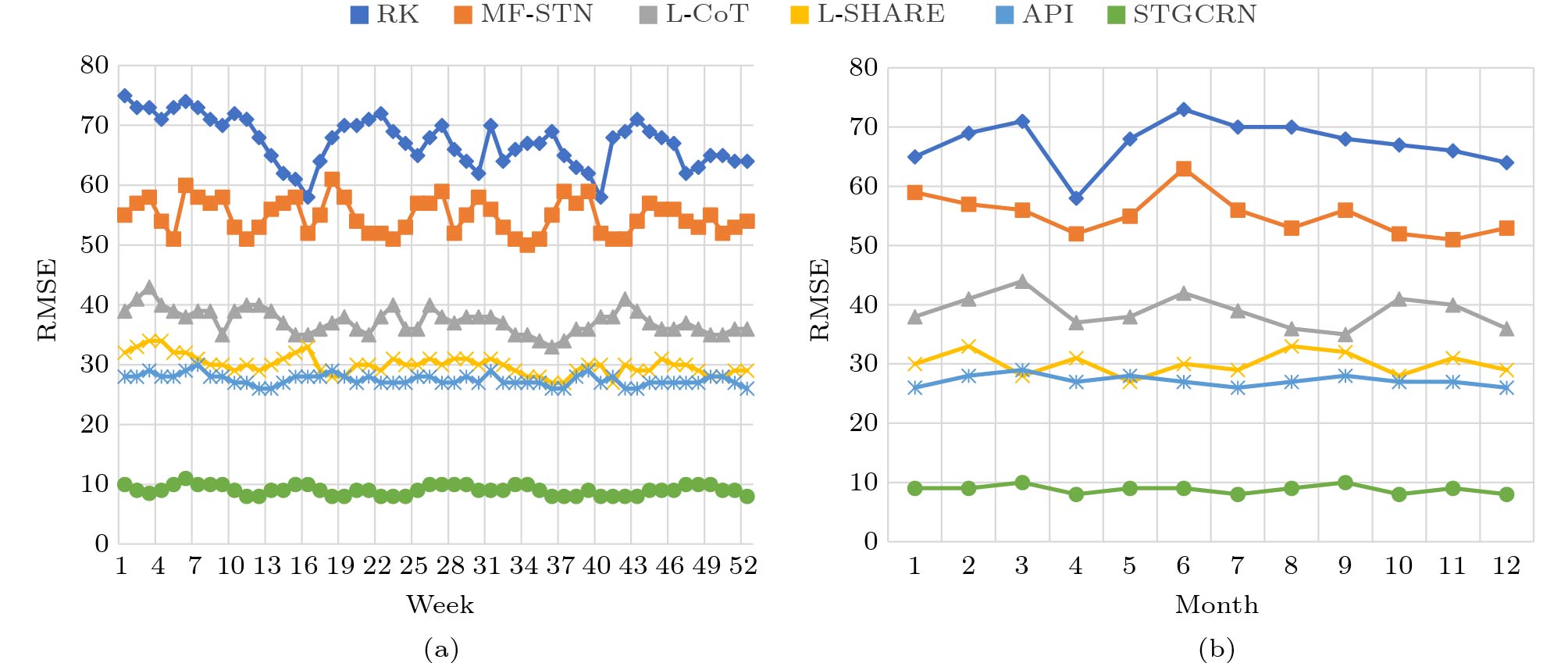
To investigate the prediction stability over time, we present the weekly and monthly performance of BSP in Fig.5 and Fig.6. As expected, the Acc and RMSE of STGCRN are stably superior to those of all the competitors, which especially reflects so during the time period of a month, and the stability performance is not directly affected by the number of time slots. We argue that such promising results are not due to the multi-domain spatio-temporal features that are carefully designed, but the learning of attention mechanism and LSTM that separately capture the spatial correlations and temporal dependencies, as well as approximation of missing popularity and characteristic fusion. Thus these efforts ensure a better performance on model learning when the dataset is naturally uneven and sparse across different time slots. However, the other deep learning based approaches (e.g., L-CoT and L-SHARE) that only capture conventional characteristics and adopt relatively deficient models, present successively inferior results in unsatisfactory environments.
Looking further into the results, one extra interesting finding is that RK clearly achieves better stable performance in terms of both weekly and monthly time periods, but it turns out the lowest Acc and the highest RMSE compared with other approaches as shown in Tables 4-7. We think this is because RK is a linear-based spatial interpolation model, which rarely acknowledges any other significant influencing features for popularity prediction. Therefore, it results in the worst effectiveness performance.
6.4.3 Ranking Evaluation
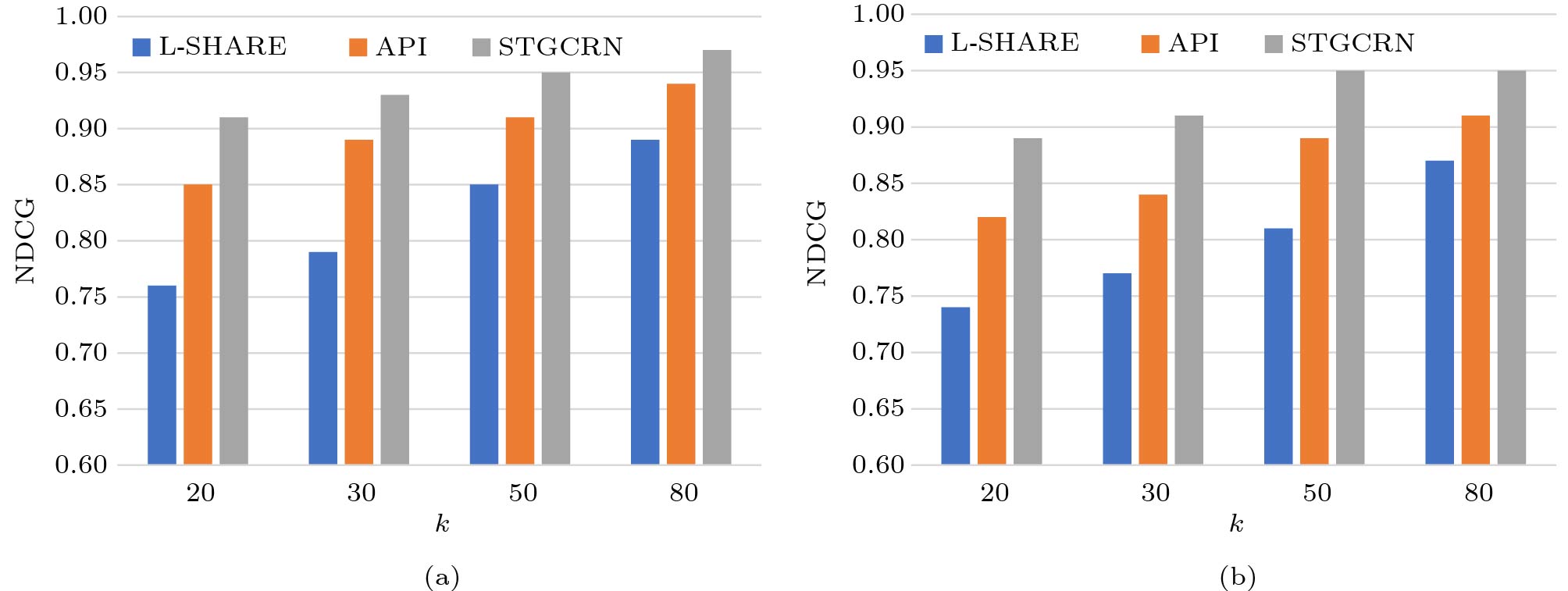
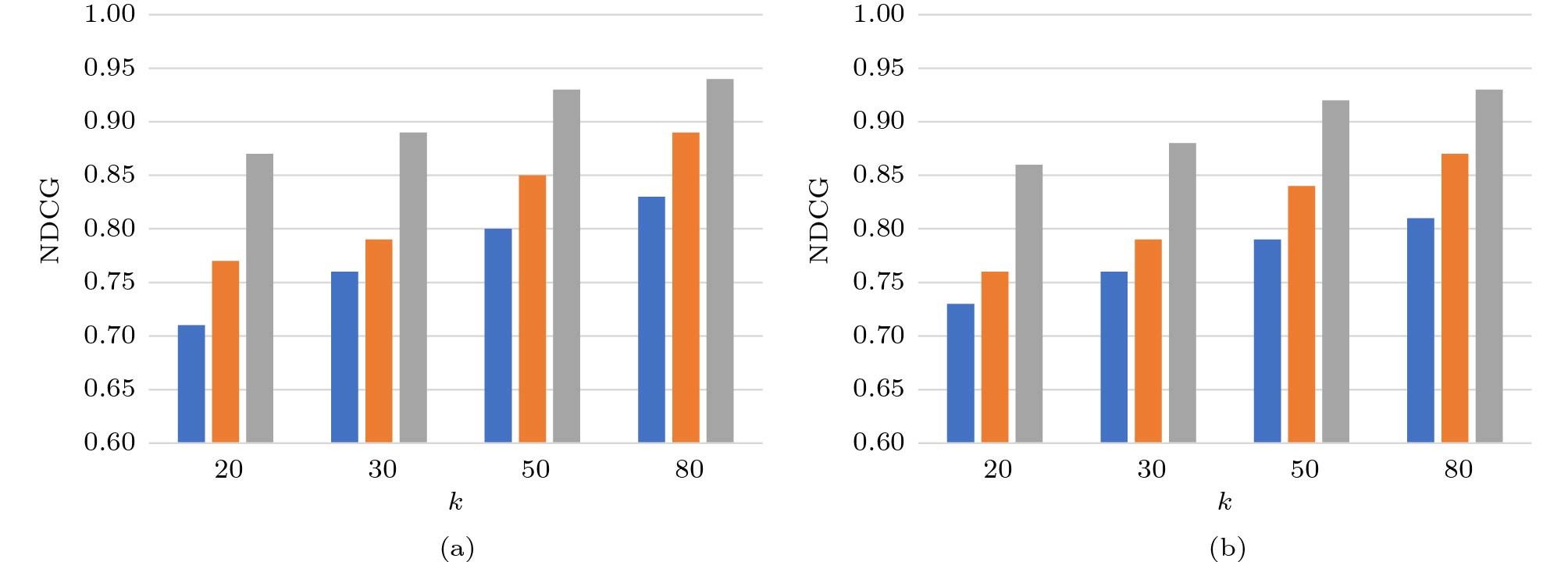
In order to examine the ranking effectiveness of recommended top- k popular candidate locations, we follow the experimental setting of Geo-Spotting[1] and API[5] for the two most related deep learning models (i.e., L-SHARE and API) under BSP and SBS with varied k , where the results are reported in Fig.7 and Fig.8.
As expected, our proposed STGCRN consistently achieves the best performance against the two competing baselines under all conditions. The reason is that STGCRN takes into consideration three significant correlations comprehensively (local spatial correlation, global spatial correlation, and dynamic temporal dependency), and also introduces an approximation block, which jointly facilitates a better popularity prediction performance of candidate locations and provide the most relevant recommendation lists. Therefore, we believe STGCRN can be quite effective for the top- k candidate location recommendation for urban facility placement, compared with state-of-the-art baselines.
6.4.4 Parameter Sensitivity
To further study the impact of different hyper-parameters of the proposed model, we evaluate STGCRN based on BSP by varying the four most important parameters: the historical time steps T_{\rm h} , the prediction time steps T_{\rm f} , the ratio of locations within urban facilities and popularity (labeled locations), and the number of attention heads in MGAT. When we vary a hyper-parameter, the others are set to default values as in Subsection 6.1.2.
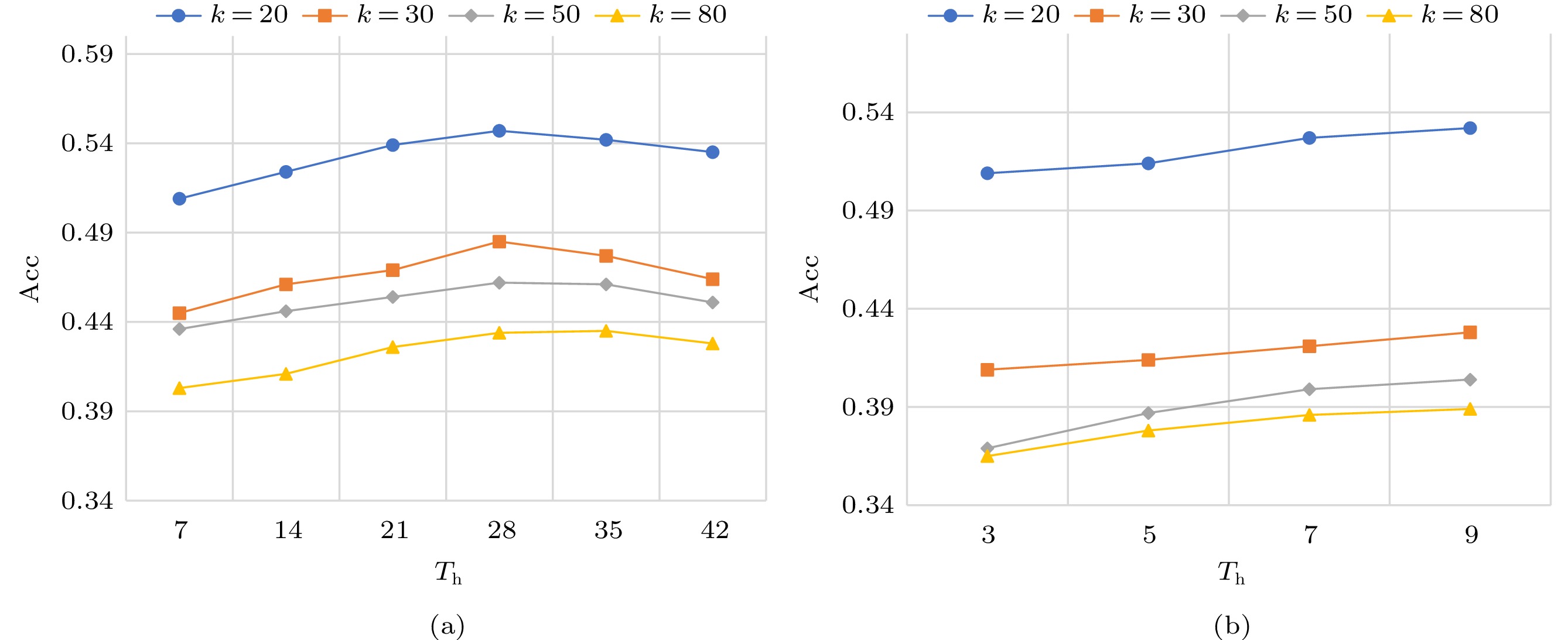
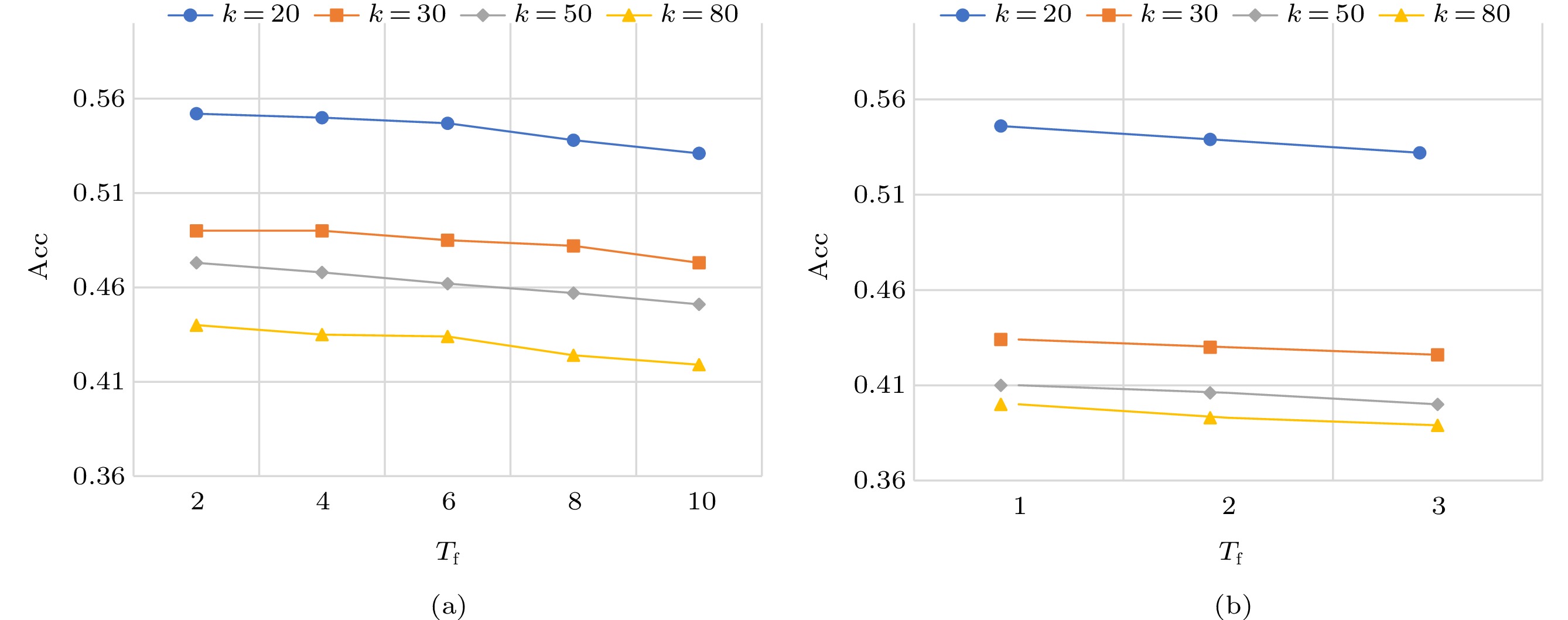
Varying T_{\rm h} . We evaluate the effect of historical input time steps T_{\rm h} in different k (i.e., 20, 30, 50, and 80), where T_{\rm h} varies from 7 to 42 weekly and 3 to 9 monthly, respectively. As shown in Fig.9, the weekly performance steadily improves when T_{\rm h} increases from 7 to 28 but the performance has a degradation when T_{\rm h} further rises from 28 to 42 as shown in Fig.9(a). This is because a relatively short input of characteristics cannot provide sufficient temporal-depended information in the LSTM blocks, whereas an excessively long-term historical input brings more noise to temporal dependency modeling. However, there are still significant performance improvements by increasing T_{\rm h} as displayed in Fig.9(b). We argue that collecting more monthly characteristics of locations enables us to acquire more accurately predicted popularity, but the effectiveness performance can eventually diminish as too long monthly input is introduced, as illustrated in Fig.9(a).
Varying T_{\rm f} . The results of the impact of prediction steps are shown in Fig.10. As expected, the overall predicted accuracy decreases slightly and consistently by increasing T_{\rm f} with varied k . We think such understandable results are due to the successive rise of noise among all locations with the increase of T_{\rm f} in weekly and monthly predictions. However, the degradation trends are acceptable due to our well-modeled STGCRN. For instance, there is only, on average, a 4.17% decrease in accuracy performance as shown in Fig.10(a), while the predicted future steps grow from 2 to 10.
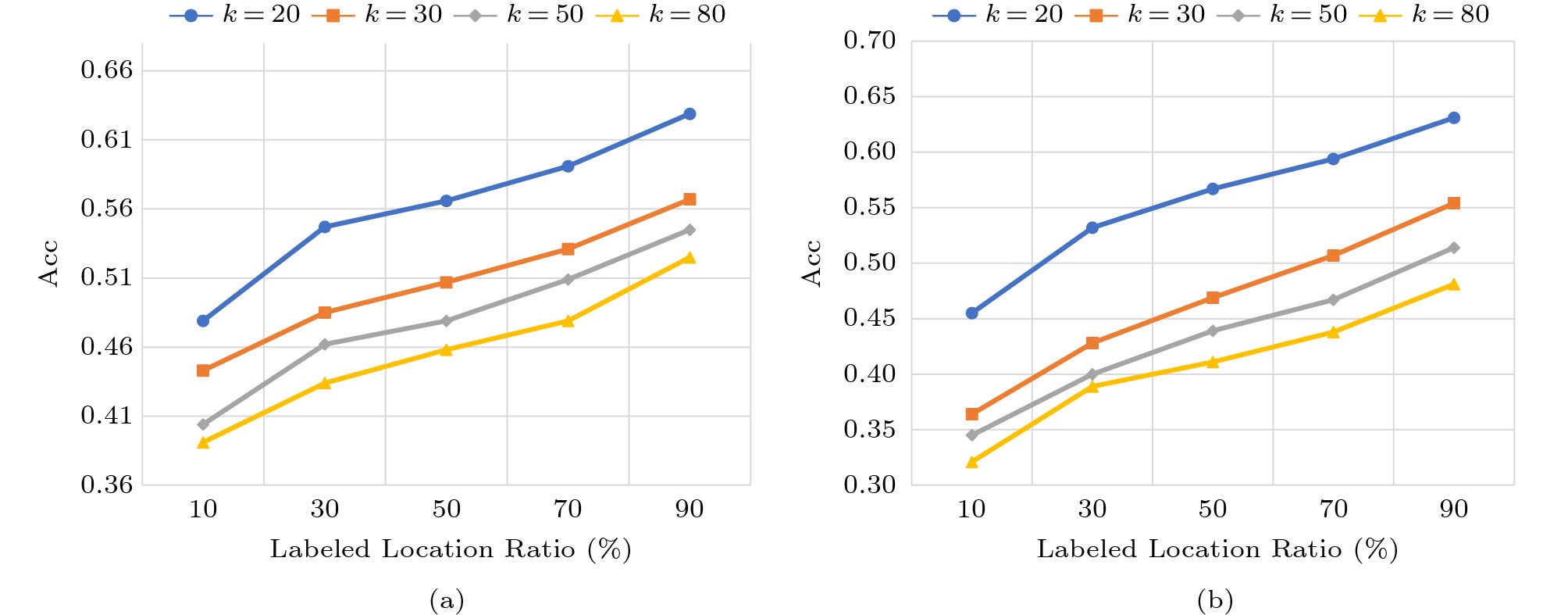
Varying the Ratio of Labeled Locations. To test the effect of the ratio of labeled locations (i.e., \left| {L_l} \right| / \left| {L} \right| ), we vary the proportion from 10% to 90%. The results are presented in Fig.11. As can be seen, employing more locations with popularity can progressively increase the accuracy of both weekly and monthly predictions. There are two major reasons for this remarkable results: a more precise model can be trained due to the increasing number of labeled locations, and the missing popularity approximation block can be more accurately learned based on the more abundant available popularity data. However, obtaining an enormous number of popularity-available locations in urban can lead to extra economic costs and may be constrained by privacy policies. Additional factors should be acknowledged to balance both the prediction effectiveness and data-collecting costs.
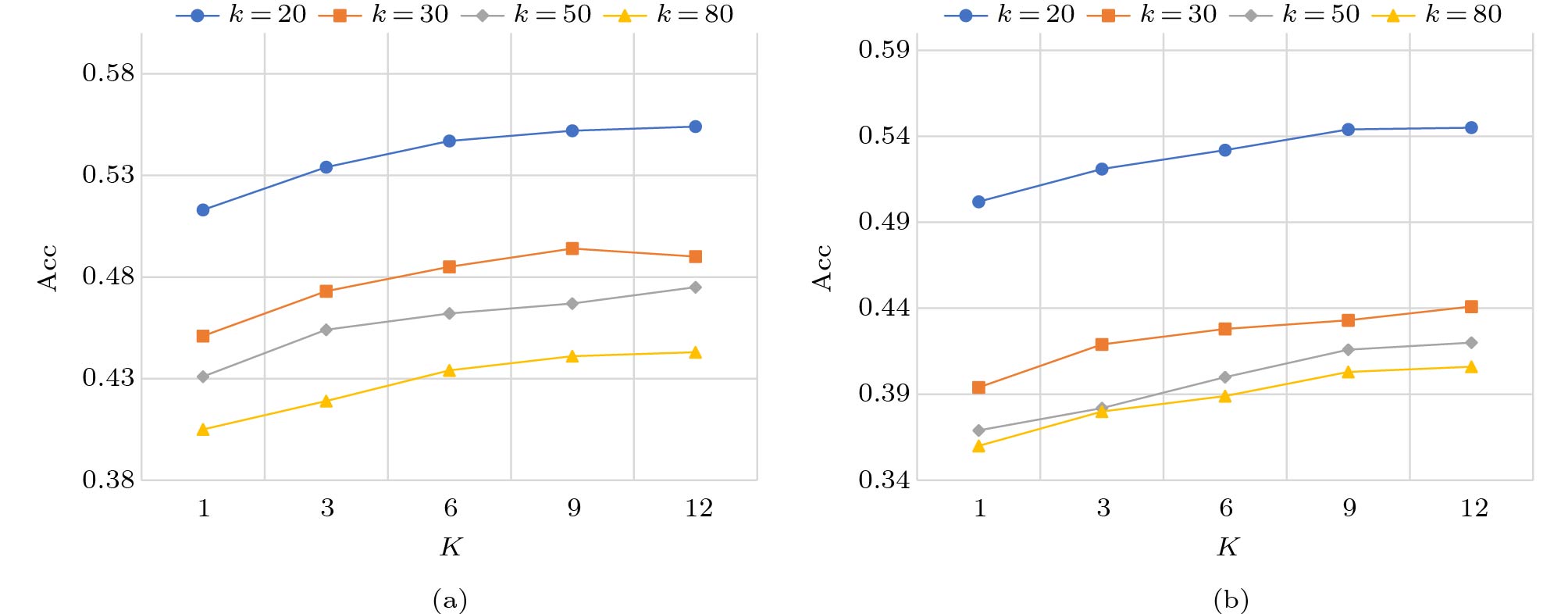
Varying K . We vary the attention head K from 1 to 12 for weekly and monthly predictions. As illustrated in Fig.12, employing more attention heads enables the proposed STGCRN to be more accurate in popularity prediction, but the improvement in accuracy begins to moderate when K = 6 in Fig.12(a) and K = 9 in Fig.12(b), respectively. One possible reason is that only a portion of attention heads in MGAT is essential and confident for the prediction task, and these “effective” heads potentially focus on different parts of LCG, which makes it possible to express sophisticated correlations, including attending to adjacent locations and then tracking spatio-temporal dependencies. Therefore, unimportant attention heads can be dropped for efficiency without significantly affecting the prediction performance.
7. Conclusions
In this paper, we developed STGCRN, a novel semi-supervised deep learning framework, with the goal of fine-grain popularity prediction. STGCRN first partitions an urban space into spatial neighborhoods, where each one is centered around a specific location, extracts corresponding features, and then forms a location correlation graph. Next, a contextual graph convolution module was introduced to incorporate both local and global spatial correlations of locations, and a recurrent neural network was further proposed to capture temporal dependencies between locations. Finally, a missing popularity approximation block was employed to predict location popularity from both the spatial and temporal domains. Extensive experiments conducted on two real-world datasets of Beijing and New York, demonstrated the superiority of our proposed STGCRN with proven effectiveness, stability, and ranking quality. Based on the location popularity prediction, we can obtain well-ranked candidate location lists for facility placement. Based on this study, we are motivated to explore the updates to candidate locations and dwellers in the future.
-
Table 1 Definition of Notations
Notation Definition l Particular location \tau Route trajectory G_s Social network {\cal{X}} Contextual characteristics {\cal{Y}} Historical popularity \tilde{y} Predicted popularity {\cal{F}}( \cdot ) Mapping function r Urban region {\cal{G}} Location correlation graph {Si}({r_i},{r_j}) Semantic similarity of r_i and r_j {{\boldsymbol{x}}}_{l_i}^{l,t} Local spatial implicit feature {{\boldsymbol{x}}}_{l_i}^{g,\ t} Global spatial implicit feature {{\boldsymbol{h}}}_{l_i}^{t} Temporal hidden state {{{\boldsymbol{y}}}}_{l_i}^{{\rm sdl},\ t} Local spatial popularity {{{\boldsymbol{y}}}}_{l_i}^{{\rm sdg},\ t} Global spatial popularity {\boldsymbol{y}}_{l_i}^{{\rm td},\ t} Approximated temporal popularity \boldsymbol{y}_{l_i}^{f,\ t} Fused popularity distribution Table 2 Summary of Dataset Statistics
Dataset Number of
Road
IntersectionsNumber of
Road
SegmentsNumber of
Candidate
LocationsNumber of
Customers/
TrajectoriesNumber of
Social
Network NodesNumber of
Social
RelationshipsNumber of
POI
Check-insBJCD 136903 176384 110102 13936 709671 3530549 3547711 NYMD 5310 6891 5008 3381 71817 1414519 836482 Table 3 Statistics of Existing Facilities
Facility Number of
StoresNumber of
Check-insNumber of
Average Check-insBSP 416 387025 930 CUSH 585 237123 405 VCS 729 319957 439 SBS 203 104681 516 7-11 118 19548 166 MDS 84 39069 465 Table 4 Effectiveness Evaluation in BJCD w.r.t. k = 30
Method BSP CUSH VCS Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.17 63.10 0.16 71.67 0.15 68.77 0.13 78.67 0.14 72.34 0.15 76.07 MF-STN 0.25 52.48 0.19 58.24 0.26 53.49 0.20 63.51 0.27 56.52 0.22 60.33 L-CoT 0.28 37.38 0.24 44.71 0.30 40.70 0.22 51.08 0.25 31.11 0.25 49.15 L-SHARE 0.39 28.55 0.36 36.37 0.39 29.14 0.29 40.22 0.35 32.89 0.32 43.90 API 0.41 25.79 0.35 22.32 0.38 28.12 0.32 28.88 0.38 27.36 0.35 29.16 STGCRN-GA 0.42 20.09 0.35 21.65 0.40 22.60 0.33 28.61 0.40 23.92 0.37 28.39 STGCRN-A 0.44 14.41 0.38 19.06 0.42 17.31 0.35 24.70 0.43 18.55 0.38 22.14 STGCRN 0.49 8.92 0.43 15.19 0.45 11.66 0.40 19.41 0.48 10.13 0.41 18.85 Table 5 Effectiveness Evaluation in NYMD w.r.t. k = 30
Method SBS 7-11 MDS Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.21 67.04 0.18 77.13 0.19 63.99 0.19 85.20 0.23 69.97 0.20 79.19 MF-STN 0.31 54.83 0.23 63.75 0.30 53.10 0.21 66.58 0.28 55.18 0.24 64.77 L-CoT 0.33 41.98 0.24 49.28 0.34 39.84 0.27 48.19 0.31 43.72 0.28 59.11 L-SHARE 0.37 30.67 0.28 40.39 0.35 29.04 0.30 44.81 0.37 28.30 0.29 42.74 API 0.39 23.10 0.33 25.61 0.38 25.22 0.35 29.03 0.38 24.22 0.36 32.66 STGCRN-GA 0.41 20.33 0.36 22.69 0.38 24.77 0.37 25.82 0.41 22.14 0.38 28.79 STGCRN-A 0.42 17.84 0.38 19.01 0.40 20.37 0.38 24.20 0.43 18.65 0.39 25.94 STGCRN 0.46 12.71 0.44 14.30 0.43 16.47 0.42 20.77 0.45 15.01 0.42 21.31 Table 6 Effectiveness Evaluation Using BSP in BJCD w.r.t. Varied k
Method k = 20 k = 30 k = 50 k = 80 Week Month Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.19 60.46 0.20 61.82 0.17 63.10 0.16 71.67 0.14 82.21 0.13 85.63 0.11 89.77 0.09 107.25 MF-STN 0.24 49.86 0.22 47.75 0.25 52.48 0.19 58.24 0.21 65.76 0.18 69.55 0.19 72.10 0.15 84.52 L-CoT 0.27 38.90 0.25 45.24 0.28 37.38 0.24 44.71 0.27 51.60 0.23 56.30 0.24 61.38 0.21 69.71 L-SHARE 0.41 26.17 0.34 37.72 0.39 28.55 0.36 36.37 0.35 37.23 0.32 45.58 0.29 53.14 0.27 58.44 API 0.45 22.33 0.40 25.41 0.41 25.79 0.35 22.32 0.37 21.86 0.32 40.41 0.34 45.02 0.29 57.19 STGCRN-GA 0.48 18.93 0.45 19.17 0.42 20.09 0.35 21.65 0.40 16.19 0.34 26.09 0.37 30.50 0.32 43.63 STGCRN-A 0.50 15.35 0.47 16.96 0.44 14.41 0.38 19.06 0.41 11.78 0.37 23.13 0.38 24.41 0.35 34.11 STGCRN 0.55 8.19 0.53 10.70 0.49 8.92 0.43 15.19 0.46 10.04 0.40 19.96 0.43 15.14 0.39 22.67 Table 7 Effectiveness Evaluation Using SBS in NYMD w.r.t. Varied k
Method k = 20 k = 30 k = 50 k = 80 Week Month Week Month Week Month Week Month Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE Acc RMSE RK 0.25 60.31 0.22 65.28 0.21 67.04 0.18 77.13 0.20 70.07 0.15 84.93 0.15 89.60 0.11 103.99 MF-STN 0.34 50.49 0.29 58.50 0.31 54.83 0.23 63.75 0.27 64.60 0.19 79.64 0.22 76.82 0.14 91.02 L-CoT 0.35 48.87 0.33 40.04 0.33 41.98 0.24 49.28 0.31 56.03 0.23 73.90 0.29 55.88 0.20 77.08 L-SHARE 0.40 23.79 0.36 32.21 0.37 30.67 0.28 40.39 0.34 47.41 0.24 62.23 0.32 50.25 0.22 70.89 API 0.44 18.32 0.41 22.12 0.39 23.10 0.33 25.61 0.36 45.45 0.29 48.51 0.35 47.77 0.27 54.01 STGCRN-GA 0.45 15.03 0.42 18.20 0.41 20.33 0.36 22.69 0.39 35.21 0.32 40.54 0.37 36.10 0.30 43.33 STGCRN-A 0.47 11.77 0.44 14.97 0.42 17.84 0.38 19.01 0.40 33.95 0.35 36.09 0.38 32.47 0.34 37.57 STGCRN 0.53 8.17 0.50 9.71 0.46 12.71 0.44 14.30 0.43 22.10 0.39 27.15 0.42 23.36 0.37 31.44 -
[1] Karamshuk D, Noulas A, Scellato S, Nicosia V, Mascolo C. Geo-spotting: Mining online location-based services for optimal retail store placement. In Proc. the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2013, pp.793–801. DOI: 10.1145/2487575.2487616.
[2] Wang F, Chen L, Pan W. Where to place your next restaurant?: Optimal restaurant placement via leveraging user-generated reviews. In Proc. the 25th ACM International Conference on Information and Knowledge Management, Oct. 2016, pp.2371–2376. DOI: 10.1145/2983323.2983696.
[3] Xu M, Wang T, Wu Z, Zhou J, Li J, Wu H. Demand driven store site selection via multiple spatial-temporal data. In Proc. the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Oct. 31–Nov. 3, 2016, Article No. 40. DOI: 10.1145/2996913.2996996.
[4] Mitra S, Saraf P, Bhattacharya A. TIPS: Mining top-k locations to minimize user-inconvenience for trajectory-aware services. IEEE Trans. Knowledge and Data Engineering, 2021, 33(3): 1238–1250. DOI: 10.1109/TKDE.2019.2935448.
[5] Hsieh H P, Lin F, Li C T, Yen I E H, Chen H Y. Temporal popularity prediction of locations for geographical placement of retail stores. Knowledge and Information Systems, 2019, 60(1): 247–273. DOI: 10.1007/s10115-018-1311-x.
[6] Ma Y, Mao J, Ba Z, Li G. Location recommendation by combining geographical, categorical, and social preferences with location popularity. Information Processing & Management, 2020, 57(4): 102251. DOI: 10.1016/j.ipm.2020.102251.
[7] Wang P, Chen W, Zhao L. Towards effective top-k location recommendation for business facility placement. In Proc. the 13th International Conference on Knowledge Science, Engineering and Management, Aug. 2020, pp.51–63. DOI: 10.1007/978-3-030-55393-7_5.
[8] Wang P, Chen W, Huang J, Wei Y, Fang J, Zhao L. Location prediction for facility placement by incorporating multi-characteristic information. Intelligent Data Analysis, 2021, 25(5): 1187–1210. DOI: 10.3233/IDA-205420.
[9] Zhou J, Cui G, Hu S, Zhang Z, Yang C, Liu Z, Wang L, Li C, Sun M. Graph neural networks: A review of methods and applications. AI Open, 2020, 1: 57–81. DOI: 10.1016/j.aiopen.2021.01.001.
[10] Zaremba W, Sutskever I, Vinyals O. Recurrent neural network regularization. arXiv: 1409.2329, 2014. https://arxiv.org/abs/1409.2329, Sept. 2024.
[11] Hochreiter S, Schmidhuber J. Long short-term memory. Neural Computation, 1997, 9(8): 1735–1780. DOI: 10.1162/neco.1997.9.8.1735.
[12] Cho K, van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, Bengio Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In Proc. the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Oct. 2014, pp.1724–1734. DOI: 10.3115/v1/D14-1179.
[13] Li X, Čeikute V, Jensen C S, Tan K L. Trajectory based optimal segment computation in road network databases. In Proc. the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Nov. 2013, pp.396–399. DOI: 10.1145/2525314.2525444.
[14] Mitra S, Saraf P, Sharma R, Bhattacharya A, Ranu S, Bhandari H. NetClus: A scalable framework for locating top-k sites for placement of trajectory-aware services. In Proc. the 33rd International Conference on Data Engineering, Apr. 2017, pp.87–90. DOI: 10.1109/ICDE.2017.46.
[15] Li Y, Bao J, Li Y, Wu Y, Gong Z, Zheng Y. Mining the most influential k-location set from massive trajectories. In Proc. the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Oct. 31–Nov. 3, 2016, Article No. 51. DOI: 10.1145/2996913.2997009.
[16] Ruan S, Bao J, Liang Y, Li R, He T, Meng C, Li Y, Wu Y, Zheng Y. Dynamic public resource allocation based on human mobility prediction. Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 2020, 4(1): Article No. 25. DOI: 10.1145/3380986.
[17] Pan Z, Wang Z, Wang W, Yu Y, Zhang J, Zheng Y. Matrix factorization for spatio-temporal neural networks with applications to urban flow prediction. In Proc. the 28th ACM International Conference on Information and Knowledge Management, Nov. 2019, pp.2683–2691. DOI: 10.1145/3357384.3357832.
[18] Hsieh H P, Lin S D, Zheng Y. Inferring air quality for station location recommendation based on urban big data. In Proc. the 21st ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2015, pp.437–446. DOI: 10.1145/2783258.2783344.
[19] Zheng Y, Liu F, Hsieh H P. U-air: When urban air quality inference meets big data. In Proc. the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2013, pp.1436–1444. DOI: 10.1145/2487575.2488188.
[20] Liu Q, Wu S, Wang L, Tan T. Predicting the next location: A recurrent model with spatial and temporal contexts. In Proc. the 30th AAAI Conference on Artificial Intelligence, Feb. 2016, pp.194–200. DOI: 10.1609/aaai.v30i1.9971.
[21] Luo Y, Liu Q, Liu Z. STAN: Spatio-temporal attention network for next location recommendation. In Proc. the 2021 Web Conference, Apr. 2021, pp.2177–2185. DOI: 10.1145/3442381.3449998.
[22] Zheng B, Hu Q, Ming L, Hu J, Chen L, Zheng K, Jensen C S. SOUP: Spatial-temporal demand forecasting and competitive supply in transportation. IEEE Trans. Knowledge and Data Engineering, 2023, 35(2): 2034–2047. DOI: 10.1109/TKDE.2021.3110778.
[23] Wang X, Ma Y, Wang Y, Jin W, Wang X, Tang J, Jia C, Yu J. Traffic flow prediction via spatial temporal graph neural network. In Proc. the 2020 Web Conference, Apr. 2020, pp.1082–1092. DOI: 10.1145/3366423.3380186.
[24] Zhang W, Liu H, Liu Y, Zhou J, Xiong H. Semi-supervised hierarchical recurrent graph neural network for city-wide parking availability prediction. In Proc. the 34th AAAI Conference on Artificial Intelligence, Feb. 2020, pp.1186–1193. DOI: 10.1609/aaai.v34i01.5471.
[25] Guo S, Lin Y, Feng N, Song C, Wan H. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. In Proc. the 33rd AAAI Conference on Artificial Intelligence, Jan. 27–Feb. 1, 2019, pp.922–929. DOI: 10.1609/aaai.v33i01.3301922.
[26] Bai L, Yao L, Wang X, Li C, Zhang X. Deep spatial-temporal sequence modeling for multi-step passenger demand prediction. Future Generation Computer Systems, 2021, 121: 25–34. DOI: 10.1016/j.future.2021.03.003.
[27] Geng X, Li Y, Wang L, Zhang L, Yang Q, Ye J, Liu Y. Spatiotemporal multi-graph convolution network for ride-hailing demand forecasting. In Proc. the 33rd AAAI Conference on Artificial Intelligence, Jan. 27–Feb. 1, 2019, pp.3656–3663. DOI: 10.1609/aaai.v33i01.33013656.
[28] Liu H, Han J, Fu Y, Li Y, Chen K, Xiong H. Unified route representation learning for multi-modal transportation recommendation with spatiotemporal pre-training. The VLDB Journal, 2023, 32(2): 342–350. DOI: 10.1007/s00778-022-00748-y.
[29] Wang X, Sun G, Fang X, Yang J, Wang S. Modeling spatio-temporal neighbourhood for personalized point-of-interest recommendation. In Proc. the 31st International Joint Conference on Artificial Intelligence, Jul. 2022, pp.3530–3536. DOI: 10.24963/ijcai.2022/490.
[30] Li M, Zhu Z. Spatial-temporal fusion graph neural networks for traffic flow forecasting. In Proc. the 35th AAAI Conference on Artificial Intelligence, Feb. 2021, pp.4189–4196. DOI: 10.1609/aaai.v35i5.16542.
[31] Park H S, Jun C H. A simple and fast algorithm for K-medoids clustering. Expert Systems with Applications, 2009, 36(2): 3336–3341. DOI: 10.1016/j.eswa.2008.01.039.
[32] Brereton R G, Lloyd G R. Support vector machines for classification and regression. Analyst, 2010, 135(2): 230–267. DOI: 10.1039/B918972F.
[33] Wang D, Fu Y, Wang P, Huang B, Lu C T. Reimagining city configuration: Automated urban planning via adversarial learning. In Proc. the 28th International Conference on Advances in Geographic Information Systems, Nov. 2020, pp.497–506. DOI: 10.1145/3397536.3422268.
[34] Tobler W. On the first law of geography: A reply. Annals of the Association of American Geographers, 2004, 94(2): 304–310. DOI: 10.1111/j.1467-8306.2004.09402009.x.
[35] Haklay M, Weber P. OpenStreetMap: User-generated street maps. IEEE Pervasive Computing, 2008, 7(4): 12–18. DOI: 10.1109/MPRV.2008.80.
[36] Hengl T, Heuvelink G B M, Stein A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma, 2004, 120(1/2): 75–93. DOI: 10.1016/j.geoderma.2003.08.018.
-
其他相关附件
-
本文附件外链
https://rdcu.be/d6X8R -
PDF格式
2024-6-13-2608-Highlights 点击下载(173KB)
-




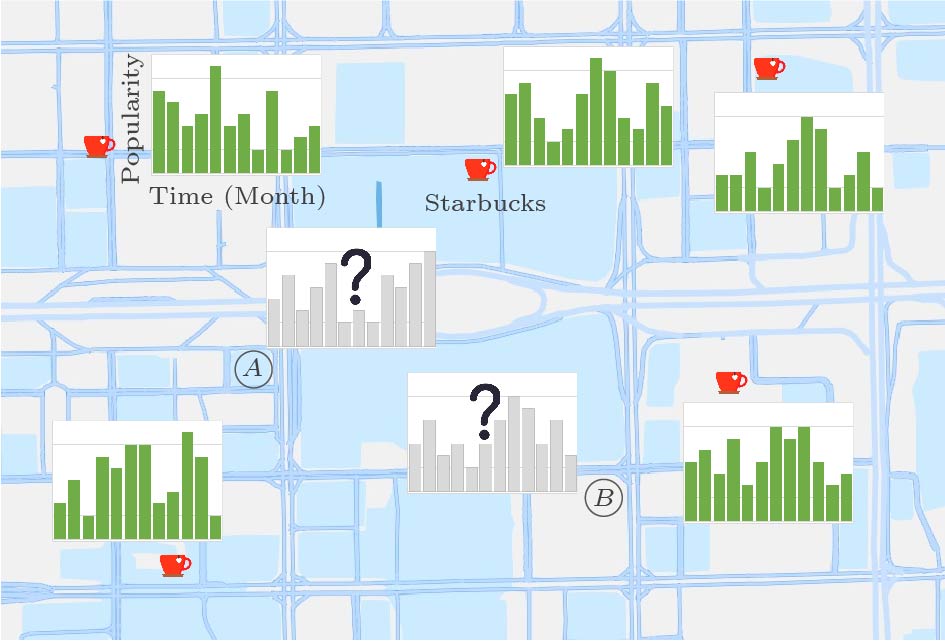
 下载:
下载: