移动群智感知环境下迭代博弈中社会福利的单边控制方法
-
摘要:研究背景
移动群智感知是常见的感知数据的一种方式。在群智感知应用中,群智感知平台与互联网服务提供商(Internet service provider, ISP)之间的交互可以被视为博弈,社会福利是群智感知中很重要的一个指标,因此有必要研究不同策略下的社会福利控制问题,为决策者提供决策支持。
目的在车辆群智感知场景下的迭代博弈中,提出适用的零行列式策略,使得群智感知平台单方面控制社会福利而不考虑对手的策略,旨在实现稳定和尽可能最大化的社会福利。
方法受益于博弈论中的零行列式策略,我们提出了一种适用于车辆群智感知平台的零行列式策略(ZD-VCS),该策略可以推导出群智感知平台的预期收益与互联网服务提供商的预期收益之间的线性关系,在此基础上设置适当的参数来获得ZD-VCS策略,并推导离散和连续模型中的ZD-VCS策略的计算方法。另外,我们研究了ZD-VCS的一种变体-勒索策略,来控制感知平台和ISP之间收益期望的比率。
结果为了验证ZD-VCS策略对社会福利控制的有效性,我们使用Taxi-Roma数据集进行仿真实验,将ZD-VCS与典型的策略进行比较,实验结果表明群智感知平台使用ZD-VCS策略可以单方面控制社会福利,带来较高且稳定的社会福利值
结论1、本文将车辆群智感知平台与互联网服务提供商之间的互动当做一个迭代博弈,解决了该博弈中的社会福利控制问题。在不考虑互联网服务提供商的策略的情况下,本文提出了一种用于车辆众感平台(ZD-VCS)的零行列式策略,用来控制整体社会福利。在这种零行列式策略下,无论网络服务提供商采取何种策略,该平台都能获得稳定且尽可能大的社会福利。实验结果验证了采用ZD-VCS策略的感知平台对社会福利实现了单边控制。未来,我们将研究零行列式策略的不同变体,并将其应用于其他场景。
Abstract:Mobile crowdsensing is a popular platform that takes advantage of the onboard sensors and resources on mobile nodes. The crowdsensing platform chooses to assign several sensing tasks each day, whose utility is based on the quality of harvested sensing data, the payment of transmitting data, and the recruitment of mobile nodes. An Internet service provider (ISP) selects a portion of access points (APs) to power on for uploading data, whose utility depends on three parts: the traffic income of transmitting sensing data, the energy cost of operating APs, and the energy cost of data transmissions by APs. The interaction between the crowdsensing platform and ISP is formulated as an iterated game, with social welfare defined as the sum of their expected utilities. In this paper, our objective is to unilaterally control social welfare without considering the opponent’s strategy, with the aim of achieving stable and maximized social welfare. To achieve this goal, we leverage the concept of a zero-determinant strategy in the game theory. We introduce a zero-determinant strategy for the vehicular crowdsensing platform (ZD-VCS) and analyze it in discrete and continuous models in the vehicular crowdsensing scenario. Furthermore, we analyze an extortion strategy between the platform and ISP. Experimental results demonstrate that the ZD-VCS strategy enables unilateral control of social welfare, leading to a high and stable value.
-
1. Introduction
With the rapid growth in various types of equipped sensors, including cameras, microphones, and GPS devices, mobile crowdsensing can now provide a wide range of services, such as urban monitoring[1], road and traffic condition monitoring[2], pollution level measurements, wildlife habitat monitoring[3], and cross-space public information sharing[4]. Particularly, vehicular crowdsensing (VCS)[5, 6] has emerged as the most promising Internet of Things (IoT) applications. VCS takes advantage of the mobility of vehicles to provide location-based services in a large-scale area, and plays a crucial role in creating a comfortable and convenient environment for urban cities.
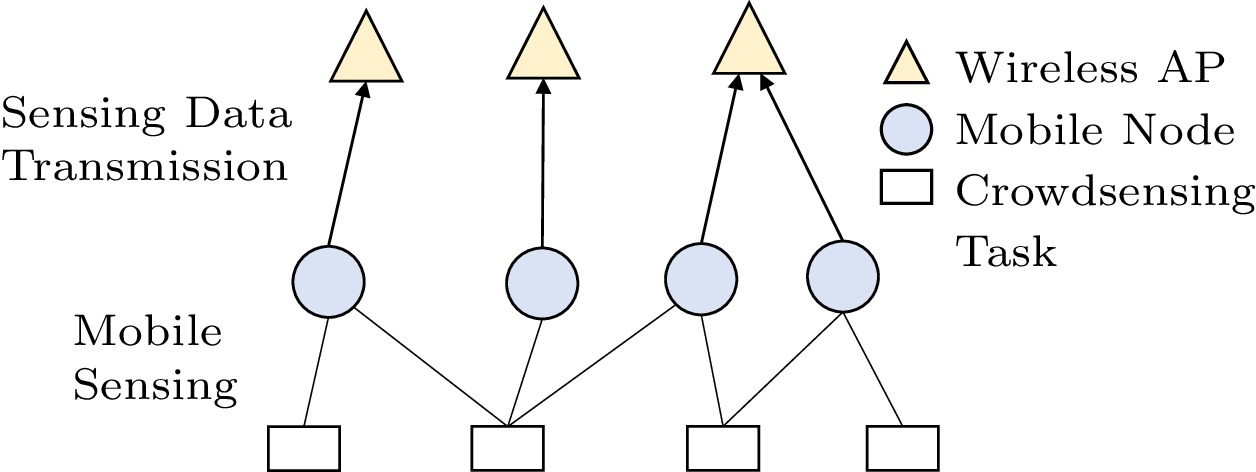
In the crowdsensing application, interactions between the crowdsensing platform and an Internet service provider (ISP) are treated as a game[7, 8]. We take vehicular crowdsensing in Fig.1 as a special case to study the game. The vehicular crowdsensing platform (simply called platform) is responsible for publishing the crowdsensing tasks. This income is determined by the quality of sensing data, which is calculated based on the quantity of sensing data and the diversity of tasks. The platform pays the traffic cost of transmitting sensing data via road-side units (RSUs) to an ISP. To reduce energy costs, the switch-mode of cell activation is widely employed[9]. Thus, the ISP schedules to partially activate RSUs for uploading the sensing data generated by the moving vehicles[10, 11]. The income of the ISP is generated from the traffic income obtained through transmitting the sensing data. When the platform publishes more tasks to cooperate, it is expected to receive a greater volume of sensing data. While the ISP activates fewer RSUs to defect, the quality of sensing data is reduced, and the platform’s income is also reduced. When the ISP activates more RSUs to cooperate, it is expected to earn more traffic income from data transmissions. However, if the platform publishes fewer tasks to defect, the income of the ISP will be reduced. Fig.1 shows an iterated game in vehicular crowdsensing where the platform and ISP interact by playing a game repeatedly (infinitely many times). On each day, the crowdsensing platform publishes the selected tasks and the ISP powers on a portion of RSUs for uploading data, independently. Based on their utilities and actions from the previous day, both of them will adjust their actions the next day according to their strategies.
In the iterated game, social welfare is defined as the sum of expected utilities of the platform and ISP. Unilateral control for social welfare in the iterated games has been discussed in much previous work. These discussions include topics like controlling social welfare (total quality of data) in mobile crowdsensing[12], addressing the crowdsourcing dilemma through social welfare control[13–15], ensuring comprehensive Quality of Services (QoS) control for all participants in wireless communication[16], unilateral control over expected payoffs for both opponents and oneself in block withholding attacks[16], and administrator-led unilateral control over the total utilities of all players in wireless network resource management[17], among others. Crowdsensing games[18–20] are ubiquitous and worth studying since crowdsensing is a widely adopted method for data sensing in various daily applications[6, 21]. Social welfare is an important metric in crowdsensing games, therefore we study the social welfare control problem with different strategies to help operators in their decision-making.
In this paper, we aim to investigate the unilateral control for social welfare of the iterated game in vehicular crowdsensing. The word “unilateral” represents that a player can control social welfare regardless of the opponent’s strategy. We consider the crowdsensing platform belonging to the government[22], who is concerned about the social welfare of the whole crowdsensing system, and thus the platform has the responsibility to control the social welfare regardless of ISP’s actions
1 2 .We discuss such unilateral control for maximizing the social welfare of the iterated game with a stable value. We prove that an equilibrium exists in each iteration of the game between the platform and ISP, but finding the equilibrium point can not achieve our goal of social welfare control.
Inspired by [15, 23], we propose a zero-determinant strategy for the Vehicular CrowdSensing platform (ZD-VCS) to control the social welfare of the crowdsensing system. The idea is that the strategy can derive a linear relationship between the expected payoff of the platform and that of the ISP, then we can set proper parameters for the to-be-adopted ZD-VCS to obtain the strategy, and the details are presented in Section 5. More specifically, we analyze the problem of unilateral control for social welfare in the discrete model. We calculate the ZD-VCS strategy that is to be adopted by the platform, regardless of ISPs’ chosen strategies (such as TFT, Pavlov, random and evolved strategy). In a discrete case, ZD-VCS takes the form of a probability vector. In a continuous case, where the payoff function is continuous, ZD-VCS becomes a piece-wise function used to calculate the probability of cooperation. Each element of the strategy represents the probability of cooperation in the current round based on the actions taken in the previous round, and the probability is calculated by the payoff functions of the platform and ISP. Actions of the platform or the ISP in each iteration are calculated by their strategies. Furthermore, we propose an extortion strategy to control the ratio of the expected utilities between the platform and the ISP. Our main contributions are summarized as follows.
1) We formulate the interactions between the platform and ISP as an iterated game and verify that an equilibrium exists in each iteration of the game.
2) To help the platform establish unilaterally control, we propose the ZD-VCS strategy and analyze it in both discrete and continuous models. Furthermore, we study an extortion strategy, which enforces an extortion relationship between the platform’s and the ISP’s expected utilities.
3) We implement the ZD-VCS strategy with real trace driven simulations. By setting proper parameters for the to-be-adopted ZD-VCS, experimental results show that the platform can control social welfare to achieve a high and stable value, and a ratio between the platform’s and the ISP’s expected utilities.
This paper is organized as follows. In Section 2, we survey the related work. Section 3 presents the preliminaries of the Zero-determinant strategy. Section 4 discusses the game between the crowdsensing platform and the ISP, and analyzes the game by the Markov Decision Model. Section 5 discusses the ZD-VCS strategy in discrete and continuous models. Section 6 evaluates the performance of the ZD-VCS strategy. The last section draws conclusions and presents our future work.
2. Related Work
We briefly review the related work on vehicular crowdsensing, the mobile crowdsensing game, and the zero-determinant strategy.
Vehicular Crowdsensing. There are many applications of vehicular crowdsensing. Pu et al.[24] proposed Chimera, which is an energy-efficient and deadline-aware hybrid edge computing framework for vehicular crowdsensing applications. Morselli et al.[25] developed a framework for analyzing multidimensional stochastic sampling in vehicular crowdsensing, where samples are gathered from the sensors on vehicles. This work is important for different kinds of applications based on environmental monitoring via IoT and vehicular communications. Campioni et al.[5] investigated the recruitment problems for vehicular crowdsensing and proposed several heuristics that outperform existing algorithms and obtain near-optimal solutions.
Mobile Crowdsensing Game. Mobile crowdsensing (MCS) games can be categorized into two types: repeated (iterated) and static games. Some problems in mobile crowdsensing can be formulated as games, which inspires researchers to find an efficient way to solve them using game theory. The repeated interactions between the MCS server and independent vehicles in a dynamic network were introduced as a dynamic vehicular crowdsensing game[20]. A Q-learning-based MCS payment strategy and sensing strategy are proposed for the dynamic vehicular crowdsensing game. Di Stefano et al.[19] modeled and quantified the evolutionary dynamics of human sensing behaviors through the rounds of iterated social dilemmas, and they validated the methodology in a vehicular crowdsensing scenario. An incentive mechanism for vehicular crowdsensing in the context of autonomous vehicles was presented to address the problem of sensing coverage in regions outside the planned trajectories of the AVs[18]. However, these studies focus on the interactions between task requestors and workers (users, vehicles), neglecting the role and actions of ISPs, and they applied the strategy obtained from reinforcement learning[20] or a greedy method[18] to maximize their utilities, which may fall into local optimum.
Zero-Determinant Strategy. The zero-determinant strategy can achieve different goals with different parameter settings. With the zero-determinant strategy, a player can control the total expected utilities of players as a stable value, and unilaterally set the expected utilities of an opponent or set a ratio between his/her and his/her opponent’s expected payoff, regardless of the opponent’s strategy. The zero-determinant strategy also evolves to extortion and generosity strategies[26]. Press et al.[23] proposed the zero-determinant strategy in the 2×2 Iterated Prisoner’s Dilemma game, and then the zero-determinant strategy is extended to the general 2×2 iterated game by other researchers and has been widely applied[27, 28]. Zhang et al.[29] investigated the power control problem in resource sharing among wireless users and network operators, and the network operator applied zero-determinant strategies to control social welfare. The interaction between a requestor and any workers in mobile crowdsensing was formulated as an iterated game, in order to improve data quality in mobile crowdsensing quality control[12]. Hu et al.[13] proposed a zero-determinant strategy to address the malicious attack problem in crowdsourcing. A sequential zero-determinant strategy[15] was applied for quality control in crowdsourcing. A zero-determinant strategy is also extended to multi-player multi-action iterated games[30]. A more comprehensive class of autocratic strategies was introduced[31], by extending the concept of zero-determinant strategies to iterated games with more diverse and generalized action spaces. In order to address the challenge of dimensionality that arises when the complexity of games increases, Tan et al.[32] presented a novel mathematical framework for analyzing strategic choices in repeated games with a varying number of actions or players, as well as arbitrary continuation probabilities. Our goal in this paper is to unilaterally study social welfare control in the iterated vehicular crowdsensing game.
3. Preliminaries: Zero-Determinate Strategy
The zero-determinant strategy[23] comprises a set of strategies in the general memory-one iterated game. With different parameter settings, the zero-determinant strategy can generate different strategies with different goals such as controlling the total expected utilities of players as a stable value, unilaterally controlling the other players’ payoff, or setting a ratio between its and the other players’ payoff.
We utilize a Markov chain to illustrate the zero-determinant strategy. The iterated game starts with an initial action. Actions of players in each iteration are obtained from the strategy, and each player performs an action and obtains a utility (reward) in each round. The strategies of players decide a stochastic process. The state of each player is represented by their union action from the previous round. It is proven that the long-memory players in the iterated game have no advantage over the short-memory players[23], since players in each iteration determine their actions based on the outcome of the previous round. This means that the corresponding stochastic process can be represented by a Markov chain, where the state transitions are joint probabilities calculated from the probabilistic strategies of players.
In the discrete case, the zero-determinant strategy is a probability vector. In contrast, in the continuous case (payoff function is continuous), the zero-determinant strategy is a piece-wise function to calculate the probability of cooperation. In the two cases, each probability element represents the probability of cooperation in the current round given the actions taken in the previous round, and the probability is calculated by the payoff functions in the game. A discrete case is taken as an example, and both players have two actions: {cooperation, defection} ( {c,d} for short). Their action pairs are {cc,cd,dc,dd}. Each player has a mixed strategy at each round, which denotes the probabilities for the next cooperation based on the actions taken in the previous round. Accordingly, we define the mixed strategy of player X as {\boldsymbol{p}} = (p_{1}, \;p_{2},\; p_{3},\; p_{4}) and that of his/her opponent Y as {\boldsymbol{q}} = (q_{1}, \;q_{2},\; q_{3}, \;q_{4}) . p_{i} represents that X chooses cooperation in the current round conditioned on the i -th action pair of the previous round, and q_{i} has a similar meaning. We assume the corresponding payoff matrices of X and Y are {\boldsymbol{P}}= (P_{\rm 1},\; P_2,\; P_3,\; P_4) and {\boldsymbol{Q}} = (Q_{\rm 1}, \;Q_2,\; Q_3,\; Q_4) , respectively. P_{i} (or Q_{i} ) is the utility of X (or Y ) corresponding to the i -th action pair. Let {\boldsymbol{p}} be a zero-determinant strategy. If a player adopts the zero-determinant strategy {\boldsymbol{p}} with different settings, the player can unilaterally set the expected utility of an opponent, control the total expected utilities of players as a stable value, or control a ratio between the player’s and his/her opponent’s expected payoff, etc., regardless of the strategy of his/her opponent. That is, there is a linear relationship between the expected payoff of two players. When player X adopts the zero-determinant strategy {\boldsymbol{p}} in the iterated game, {\boldsymbol{p}} satisfies the following equation:
\begin{split} &p_{i} =\left\{ \begin{array}{lc} \phi(\alpha P_{i}+ \beta Q_{i} + \gamma) +1, &\quad i =1,\;2, \\ \phi(\alpha P_{i}+ \beta Q_{i} + \gamma), &\quad i = 3,\;4, \\ \end{array} \right. \end{split} where \alpha,\; \beta,\; \gamma,\; \phi are parameters, \phi \neq 0 , and p_{i} could be calculated by the parameters and payoff matrices. No matter which strategy Y adopts, the expected payoff of X and Y ( U^{\rm x} and U^{\rm y} ) satisfies:
\begin{aligned} \alpha U^{\rm x}+ \beta U^{\rm y} + \gamma = 0. \end{aligned} (1) For example, when \alpha = 0 , U^{\rm y} is controlled by X . With different settings of parameters, (1) generates various strategies. Such strategies, which are referred to as zero-determinant strategies, are realized if the process of the game can be formulated as a one-step Markov process. The frequently-used notations are listed in Table 1.
Table 1. Description of Frequently-Used NotationsNotation Description E = \{ e_{\rm1},\; \ldots, \;e_{\rm M} \} Set of M candidate sensing tasks R = \{ r_{\rm1},\; \ldots, \; r_{\rm N} \} Set of N candidate RSUs x_{\rm e}/x_{\rm r} Number of selected sensing tasks/RSUs {\boldsymbol{W}} Task-RSU weighted traffic matrix \vec{{\boldsymbol{X}}_{\rm e}}/\vec{{\boldsymbol{X}}_{\rm r}} Vector of selected sensing tasks/RSUs f_{\rm g}/f_{\rm t} Payoff function of platform/ISP u_{\rm r}/u_{\rm t},\; C Energy cost/traffic cost, operating cost {\boldsymbol{M}}^{\rm e},\; {\boldsymbol{M}}^{\rm r} Payoff matrix of platform and ISP m^{\rm e}_{i},\; m^{\rm r}_{i} Elements in M^{\rm e} and M^{\rm r} {\boldsymbol{p}},\; {\boldsymbol{q}} Mixed strategy of platform and ISP {\boldsymbol{v}}_{\rm s}/ {\boldsymbol{f}} Stationary vector/any vector U^{\rm e}/ U^{\rm r}/ U_{\rm all} Utility of platform/ISP/both {\boldsymbol{H}} Markov state transition matrix \alpha,\;\beta,\;\gamma Parameters to determine the ZD-VCS strategy \chi Extortion factor l^{\rm r}/ l^{\rm e} Lowest number of RSU/sensing tasks h^{\rm r}/ h^{\rm e} Highest of RSU/sensing tasks 4. System Model
In this section, we introduce the mobile crowdsensing model and the game formulation between the platform and ISP.
4.1 Mobile Crowdsensing Model
Considering the general scenario of the mobile crowdsensing shown in Fig.2, there are three participants: the crowdsensing platform, mobile nodes, and wireless access points (APs). The platform is responsible for publishing crowdsensing tasks (such as monitoring the temperatures in some areas[3, 33]) and assigning tasks to mobile nodes (e.g., vehicles, mobile users). We denote the set of M sensing tasks as E = \{ e_{\rm1}, \;\ldots, \;e_{\rm M} \} . The crowdsensing platform could belong to the government[22] or a service platform company (such as Uber[34]). The recruited mobile nodes are responsible for sensing the data from the sensing tasks. The platform pays a constant operating cost (denoted as C ) to the recruited mobile nodes every day. The mobile nodes sense data passively when they are in the sensing areas, rather than actively go to the sensing areas. The incentive mechanism for mobile nodes has been proposed in [14, 35, 36], but it is out of the scope of our paper.
Wireless APs, such as Wi-Fi, femtocell
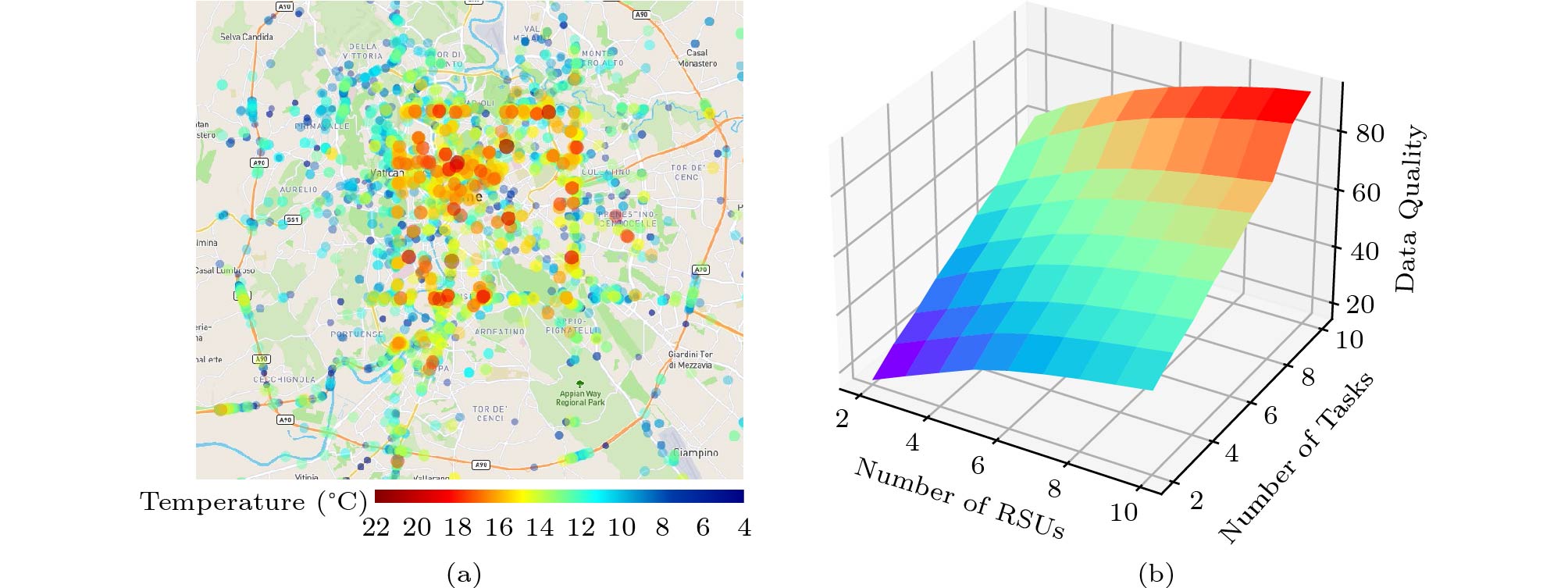
3 , Smart Pole4 , and other RSUs, are installed by the ISP and provide communication for the mobile nodes, which are denoted by R = \{ r_{\rm1}, \;\ldots, \; r_{\rm N} \} . These N APs are responsible for uploading the sensing data generated by the mobile nodes. Generally, compared with a cell-tower in cellular systems, the coverage of each AP is relatively small[37]. For example, the coverage of RSU is about 100-500 meters. As a result, it is hard to provide seamless roaming for vehicles[38], and therefore, the sensing data’s offloading will be delayed during its lifetime through an AP that acts as a gateway. If there are no available APs, some sensing data will be delayed rather than immediately sent or received through an AP. This kind of technology has been extensively investigated[39, 40]. The distributions of sensing tasks, mobile modes, and the available APs have an influence on the quality of sensing data. Data quality can only be measured when the quantity of sensing data is large enough. The quantity of sensing data is closely related to sensing tasks, mobile modes, and the available APs. When the mobile nodes sense the data in the area of a sensing task, the sensing data will be transmitted through an AP, and then the sensing data can be uploaded successfully. When the wireless APs and crowdsensing tasks belong to different operators, the interactions between the published tasks and the available APs will form a game. We formulate this game in Subsection 4.2.Fig.3(a) is an example of a temperature monitoring scenario in Rome, Italy from the real data trace
5 . The points in Fig.3(a) are the temperature data sensed by the vehicles, which is also called sensing data. The color of a point close to red refers to a place with a higher temperature, and that close to blue refers to a place with a lower temperature. On each day, the platform publishes several tasks for sensing the temperatures of some areas in Fig.1, and the ISP powers on a portion of RSUs for uploading the sensing data to save energy costs. When a vehicle passes by an area that needs to be sensed, it will generate a sensing data packet with temperature records. When a vehicle leaves the current sensing area with the sensing data and moves into the communication range of a working RSU, the sensing data packet will be uploaded to a remote cloud server via the RSU.The traffic distribution of vehicles is different each day, therefore different RSUs have different contributions to the data quality in crowdsensing. In order to measure the importance of each RSU, when assigning the sensing tasks with different priorities, we apply a matching algorithm to obtain the selected important RSUs. Thus, the number of RSUs can be used as the ISP’s action in the game, which will be formulated in the following Subsection 4.2. Fig.3(b) shows the trends of data quality in different numbers of sensing tasks and RSUs.
4.2 Game Formulation
We denote the action of assigning tasks by the platform as vector \vec{{\boldsymbol{X}}_{\rm e}} with dimension M , where the element is 0 or 1 , indicating whether a candidate task is selected or not. Let x_{\rm e} denote the number of selected tasks, i.e., x_{\rm e} = ||\vec{{\boldsymbol{X}}_{\rm e}}||_{1} . The action of operating RSUs by an ISP is denoted by vector \vec{{\boldsymbol{X}}_{\rm r}} with dimension N , where the element is 0 or 1 , indicating whether the RSU is powered on or not. Let x_{\rm r} denote the number of selected RSUs, x_{\rm r} = ||\vec{{\boldsymbol{X}}_{\rm r}}||_{1} . We denote {\boldsymbol{W}} \in \mathbb{R}^{M \times N} as a task-RSU weighted traffic matrix, where element {{W}}_{ij} is the number of sensing data uploaded by the RSU j for task i . \boldsymbol{W}^{x_{\rm{e}},\ x_{\rm{r}}}=(\vec{\boldsymbol{X}_{\rm{e}}}^{\mathrm{T}}\cdot\vec{\boldsymbol{X}_{\rm{r}}})\circ \boldsymbol{W} , which refers to the traffic distribution of x_{\rm e} sensing tasks under x_{\rm r} RSUs. The symbol \circ refers to the Hadamard product, and the element {{W}}^{x_{\rm e},x_{\rm r}}_{i,j} also represents the traffic count of the i -th sensing task under the j -th RSU.
We take an example to illustrate how to obtain the matrix {\boldsymbol{W}}^{x_{\rm e},x_{\rm r}} . In the case of \vec{{\boldsymbol{X}}_{\rm e}}=(1,\; 0, \;1,\; 1) and \vec{{\boldsymbol{X}}_{\rm r}}=(1, \;0,\; 1) , that is, M=4 , N=3 , x_{\rm e} = 3 , and x_{\rm r} = 2 . Then,
\begin{aligned} \nonumber \vec{{\boldsymbol{X}}_{\rm e}}^{\rm T} \cdot \vec{{\boldsymbol{X}}_{\rm r}}= \begin{pmatrix} 1 & 0 & 1\\ 0 & 0 & 0\\ 1 & 0 & 1\\ 1 & 0 & 1 \end{pmatrix}. \end{aligned} When {\boldsymbol{W}} is set as:
\begin{aligned} \nonumber {\boldsymbol{W}}= \begin{pmatrix} 15 & 20 & 31\\ 40 & 20 & 26\\ 20 & 20 & 18\\ 18 & 30 & 16 \end{pmatrix}, \end{aligned} {\boldsymbol{W}}^{3,\ 2} is calculated as:
\begin{aligned} \nonumber {\boldsymbol{W}}^{3,\ 2} = (\vec{{\boldsymbol{X}}_{\rm e}}^\mathrm{T} \cdot \vec{{\boldsymbol{X}}_{\rm r}})\circ {\boldsymbol{W}} = \begin{pmatrix} 15 & 0 & 31\\ 0 & 0 & 0\\ 20 & 0 & 18\\ 18 & 0 & 16 \end{pmatrix}, \end{aligned} referring to the traffic distribution of three sensing tasks under two RSUs.
We investigate the actions with different numbers of tasks and RSUs in the iterated game, and simplify each action with x_{\rm e} tasks or x_{\rm r} RSUs into a single case. Thus, we use x_{\rm e} or x_{\rm r} to represent the unique action, respectively. That is, x_{\rm e} and x_{\rm r} denote the number of selected tasks and RSUs, respectively. Generally, the sensing tasks and RSUs of different areas have different priorities, and top x_{\rm e} tasks and x_{\rm r} RSUs with higher priorities are selected. Bellow, we illustrate how to calculate the priorities.
In this paper, we use vehicular crowdsensing as a case study. We use the Taxi-Roma dataset
6 to explain how to determine the priority of crowdsensing tasks. The dataset includes the GPS coordinates of 320 taxi drivers working in the center of Rome. These GPS coordinates are collected over 30 days. The dataset is preprocessed by filtering out some outliers. The traces cover an area with a range of 66 km \times 59 km, and we divide the area into 10 \times 10 grids. We assume that each RSU in the grid serves as a gateway and each grid is viewed as an area with a sensing task. The priority of each sensing task and RSU are calculated by the number of GPS coordinates in each grid. The more GPS coordinates in a grid, the higher priority of each sensing task and RSU in this grid.4.2.1 Payoff of Platform
In our vehicular crowdsensing scenario, the platform earns values from the quality of harvested sensing data and the diversity of tasks, paying for data transmission and recruitment of vehicles. We assume that the size of each sensing data packet is the same[41]. The data quality is defined as
\begin{aligned} \nonumber Q_{\rm d}(x_{\rm e},\;x_{\rm r}) = \sum\nolimits_{i,\;j} \big(\log (W^{x_{\rm e},\;x_{\rm r}}_{i,\;j}+1) -P_{ij}\log P_{ij}\big),\; \end{aligned} where 1\leqslant i \leqslant M, 1\leqslant j \leqslant N , the term \sum_{i,\ j} {\rm log} (W^{x_{\rm e},\ x_{\rm r}}_{i,\ j} +1) reflects the growth rate of the platform’s data quality decreases (diminishing return) as the increment of sensing data[42], and the \rm log function also reflects that the redundant sensing data cannot substantially contribute to data quality. We utilize the entropy -P_{ij}\log P_{ij} to model the diversity of sensing data[43], which reflects the task and transmission diversity. The term P_{ij} = W^{x_{\rm e},\ x_{\rm r}}_{i,\ j}/\sum_{i,\ j} W_{i,\ j}^{x_{\rm e},\ x_{\rm r}} .
The utility of the vehicular crowdsensing platform depends on the data quality of the sensing data, payment of transmitting the sensing data and recruiting vehicles. We formulate the payoff function of the platform as the value of sensing data minus the costs of data transmission, and the payoff function is represented as
\begin{aligned} f_{\rm g}(x_{\rm e},x_{\rm r}) = u_{\rm d}\times Q_{\rm d}(x_{\rm e},x_{\rm r}) - u_{\rm t}\times \sum\nolimits_{i,\,j} W_{i,\,j}^{x_{\rm e},\,x_{\rm r}} - C, \end{aligned} (2) where u_{\rm d} is the benefit that per data quality could bring, u_{\rm t} is the transmission price per unit of data traffic and the constant C refers to the cost of recruiting vehicles. Note that the platform is expected to publish more tasks, so as to cover more areas with more sensing data and obtain more utilities.
4.2.2 Payoff of ISP
Fig.3(b) shows the changes of the data quality with the selected x_{\rm e} sensing tasks and x_{\rm r} RSUs from the real data trace⑥. We notice that the data quality increases with more sensing tasks and RSUs, which determines the platform’s income. To transmit more sensing data, the ISP is required to power on more RSUs, which causes more energy costs. The ISP earns the traffic income of transmitting the sensing data, and pays the energy costs of operating an RSU and data transmissions by RSUs. Thus, we formulate the payoff function of the ISP as the traffic income of sensing data minus the energy costs on RSUs as follows:
\begin{aligned} f_{\rm t}(x_{\rm e},x_{\rm r}) = (u_{\rm t}-u_{\rm e}) \times \sum\nolimits_{i,\ j} W_{i,\ j}^{x_{\rm e},\ x_{\rm r}} - x_{\rm r} u_{\rm r}, \end{aligned} (3) where x_{\rm r} represents the number of RSUs powered on, u_{\rm r} refers to the per-unit cost of operating an RSU, and u_{\rm e} refers to the average energy cost[44] to transmit each unit of sensing data.
From (2) and (3), we see that the platform’s cost of uploading sensing data is u_{\rm t}\times \sum_{i,\ j} W_{i,\ j}^{x_{\rm e},\ x_{\rm r}} , which is also the income of the ISP. In (3), when the number of sensing tasks reaches a certain level, the utility of the traffic from the sensing data is greater than the energy costs of the RSUs, and thus the ISP is willing to power on more RSUs.
4.2.3 Discussion
Fig.4 is an example of two actions in the game. Like the prisoner’s dilemma, cooperation denotes the highest number of sensing tasks or RSUs, and defection refers to the lowest one. x_{\rm e},\; x_{\rm r} \in \left\{{{cooperation}},\right. \left. {{defection}}\right\} . This example sets x_{\rm e} = x_{\rm r} = 4 when the platform and ISP cooperate and x_{\rm e} = x_{\rm r} = 2 when they defect. The value pair in Fig.4 is the utilities of the platform and the ISP. In each iteration, they move on to the next round based on the actions determined by their probabilistic strategies.
4.3 Nash Equilibrium
We analyze the equilibrium of the game between the platform and the ISP in each iteration. Proofs of all theorems are presented in the supplementary file
7 .Theorem 1. The game between the crowdsensing platform and the ISP has an equilibrium.
Theorem 2. The equilibrium point is unique in the game between the crowdsensing platform and the ISP.
Next, we take Fig.4 as an example to illustrate the equilibrium point. We can obtain equilibrium points from a solver
8 . In Fig.4, from the platform’s perspective, no matter what the ISP’s action is, the ISP’s best action is cooperation (x_{\rm e} = 4) , and similarly, the ISP’s best action is defection (x_{\rm r} = 2) . Thus, this game has an equilibrium of (20,\; 28) , where the social welfare is 20 + 28 , which is certainly less than that in the case when both the ISP and the platform cooperate. Generally, the ISP does not know how many sensing tasks the platform will publish, and therefore a selfish ISP tends to power on fewer RSUs in each game round, resulting in lower social welfare. Thus, an equilibrium point is not the optimal solution to maximize social welfare.4.4 MDP in the Iterated Game
The iterated game is viewed as a Markov decision process (MDP)[45]. For each player, an MDP is modeled as follows.
1) Action Space. The action spaces of the platform and the ISP are denoted as A_{\rm e} = \{l^{\rm e},\; h^{\rm e}\}, ( x_{\rm e} \in A_{\rm e}) and A_{\rm r} = \{l^{\rm r},\; h^{\rm r}\},\;( x_{\rm r} \in A_{\rm r}) , respectively. The platform chooses the action of assigning the highest or the lowest number of tasks, denoted as h^{\rm e} and l^{\rm e} , respectively. The ISP determines the action of providing the highest or the lowest number of RSUs, denoted as h^{\rm r} and l^{\rm r} respectively.
2) State Space. The state space is the action pairs from the previous round, and is denoted as S = \{( x_{\rm e},\; x_{\rm r})\} = \{ (h^{\rm e}h^{\rm r}),\; (h^{\rm e}l^{\rm r}),\; (l^{\rm e}h^{\rm r}),\; (l^{\rm e}l^{\rm r})\} , s_{\rm t} \in S .
3) Reward. R_{\rm e} or R_{\rm r} represent the immediate reward received by the platform and ISP after transitioning from state s to state s' , due to action a . We define the payoff matrices of the platform and ISP in each round as {\boldsymbol{M}}^{\rm e} and {\boldsymbol{M}}^{\rm r} , respectively. {\boldsymbol{M}}^{\rm e} = (f_{\rm g}(h^{\rm e},\;h^{\rm r}),\;f_{\rm g}(h^{\rm e}, l^{\rm r}),\; f_{\rm g}(l^{\rm e},\;h^{\rm r}),\; f_{\rm g}(l^{\rm e},\; l^{\rm r}))^\mathrm{T} , and {\boldsymbol{M}}^{\rm r} = (f_{\rm t}(h^{\rm e},\; h^{\rm r}),\; f_{\rm t}(h^{\rm e}, l^{\rm r}),\; f_{\rm t}(l^{\rm e},\; h^{\rm r}),\; f_{\rm t}(l^{\rm e},\; l^{\rm r}))^\mathrm{T} .
4) State Transition Probabilities. P_{a}(s,\;s') = \Pr(s_{t+1}=s'\mid s_{t}=s,\; a_{t}=a) is the probability that action a in state s at the round t will lead to state s' at the t+1 round.
A policy function \pi is a (potentially probabilistic) mapping from state space S to action space A . Once an MDP is combined with a policy, a Markov chain forms. Since the action chosen in state s is completely determined by \pi (s) , the state transition probability \Pr(s_{t+1}=s'\mid s_{t} = s,\;a_{t} = a) can reduce to \Pr(s_{t+1} = s'\mid s_{t} = s) (a Markov transition matrix).
Briefly speaking, in the Markov decision process, a player will repeatedly observe the current state s_t of the environment and take an action from all available actions in this state. Then, the state will transfer to s_{t+1} , and the agent will get a reward R_{\rm t} from the environment for the agent’s action.
In the iterated game, as RSU’s actions are variable, the social welfare can fluctuate sometimes being high and sometimes low, which makes it unstable. Thus, we aim to control social welfare at the highest stable value possible, and we model the problem of social welfare control as follows.
Problem 1 (Social Welfare Control). The social welfare is required to be controlled at a stable and maximum possible value, which indicates the social welfare is showing little change and remains around the maximum possible value as the game iterations increase.
\begin{split}&{\rm max} \quad U_{\rm all} = \alpha U^{\rm e} + \beta U^{\rm r},\\&{\rm s.t.} \qquad U^{\rm e} + U^{\rm r} = -\gamma,\\[-1pt] \end{split} (4) where \alpha and \beta refer to the weights of the expected utilities U^{\rm e} and U^{\rm r} , respectively, and \gamma is a variable in a range.
The constraint in (4) refers to the fact that the social welfare is a constant. The objective function and the constraint determine that the goal is to maintain social welfare at a stable and maximum possible value.
5. Social Welfare Control with ZD-VCS
In this section, we analyze the iterated game with the aim of controlling social welfare using the zero-determinant strategy, and then we discuss the discrete and continuous strategies.
5.1 Game Analysis: Zero-Determinant Strategy
We aim to maximize the social welfare of the iterated game at a stable value, and the social welfare is the sum of the expected payoff of the platform and the ISP. To achieve this goal, we take advantage of the zero-determinant strategy in game theory and propose a scheme named Zero-Determinant Strategy for Vehicular CrowdSensing Platform (ZD-VCS) to control social welfare. This strategy is a vector of conditional probabilities. Each element in the vector is a probability for cooperation in the current round based on the actions taken in the previous round, and the probability is calculated by the payoff functions of the platform and the ISP. Fig.4 shows the transfer process from the previous round to the current round, and p_{\rm 1}(1-q_{\rm 1}) is the probability from one state to another state. To simplify this game, we consider the discrete strategy, where the platform and the ISP adopt either an extremely amicable or a vicious action. While the continuous strategy refers to any integer action as long as it is in the corresponding continuous strategy space. It is essential to explore the integer actions because a larger action space may lead to higher social welfare.
5.2 ZD-VCS Strategy in the Discrete Model
In the discrete model, the player’s action is private at each round; thus, there are four outcomes for each game iteration. We label the four outcomes of each iteration as 1,\; 2,\; 3 , and 4 , respectively, corresponding to the four states. We assume that the two players (the platform and ISP) only have the state memory of the previous round. In the game, both players have mixed strategies at each round, denoting the cooperation probabilities under the four possible states of outcomes in the previous round. Accordingly, we define the mixed strategy of the platform as {\boldsymbol{p}} = (p_{1},\; p_{2},\; p_{3},\; p_{4}) , which is the zero-determinant strategy of the platform. The mixed strategy of the ISP is {\boldsymbol{q}} = (q_{1},\; q_{2},\; q_{3},\; q_{4}) . Here, p_{1},\; p_{2},\; p_{3},\; p_{4} and q_1,\ q_2,\ q_3,\ q_4 are the probabilities of choosing h^{\rm e} or h^{\rm r} in the current round when the outcome of the previous round is x_{\rm e}x_{\rm r} = (h^{\rm e}h^{\rm r},\; h^{\rm e}l^{\rm r},\; l^{\rm e}h^{\rm r},\; l^{\rm e}l^{\rm r}) , respectively. Fig.4 shows the probability transfer process from the previous round’s action to the current round’s action. In the current round, we denote the possibilities of the four potential states of outcomes as {\boldsymbol{v}} = (v_{1},\; v_{2},\; v_{3},\; v_{4})^\mathrm{T} , where \sum^{4}_{i=1}v_{i} = 1 . Thus, the expected payoffs of the platform and the ISP are U^{\rm e} = {\boldsymbol{v}}^\mathrm{T}{\boldsymbol{M}}^{\rm e} and U^{\rm r} = {\boldsymbol{v}}^\mathrm{T}{\boldsymbol{M}}^{\rm r} , respectively. Note that any character in bold in this paper refers to a vector or a matrix.
Based on the definitions of {\boldsymbol{p}} and {\boldsymbol{q}} , we denote the Markov state transition matrix as {\boldsymbol{H}} , and the stationary vector as {\boldsymbol{v}}_{\rm s} . {\boldsymbol{v}}^\mathrm{T}_{\rm s} {\boldsymbol{H}} = {\boldsymbol{v}}^\mathrm{T}_{\rm s} , where
\begin{aligned} \nonumber {\boldsymbol{H}}= \begin{pmatrix} p_{\rm 1}q_{\rm 1} & p_{\rm 1}(1-q_{\rm 1}) & (1-p_{\rm 1})q_{\rm 1} & (1-p_{\rm 1})(1-q_{\rm 1}) \\ p_{\rm 2}q_{\rm 2} & p_{\rm 2}(1-q_{\rm 2}) & (1-p_{\rm 2})q_{\rm 2} & (1-p_{\rm 2})(1-q_{\rm 2}) \\ p_{\rm 3}q_{\rm 3} & p_{\rm 3}(1-q_{\rm 3}) & (1-p_{\rm 3})q_{\rm 3} & (1-p_{\rm 3})(1-q_{\rm 3}) \\ p_{\rm 4}q_{\rm 4} & p_{\rm 4}(1-q_{\rm 4}) & (1-p_{\rm 4})q_{\rm 4} & (1-p_{\rm 4})(1-q_{\rm 4}) \\ \end{pmatrix}, \end{aligned} and each element in {\boldsymbol{H}} represents the transition probability from one state to another state. For example, the state p_{\rm 1}(1-q_{\rm 1}) refers to the transition probability of the game from state h^{\rm e}h^{\rm r} to state h^{\rm e}l^{\rm r} .
Inspired by [23], we suppose {\boldsymbol{H}}' = {\boldsymbol{H}} - {\boldsymbol{I}} , then {\boldsymbol{v}}^\mathrm{T}_{\rm s} {\boldsymbol{H}}' = 0 . According to Cramer’s rule, we can obtain {{Adj}}({\boldsymbol{H}}'){\boldsymbol{H}}' = {det}({\boldsymbol{H}}'){\boldsymbol{I}} = 0 , where {Adj}({\boldsymbol{H}}') denotes the adjugate matrix of {\boldsymbol{H}}' . Then, we obtain that every row of {Adj}({\boldsymbol{H}}') is proportional to {\boldsymbol{v}}_{\rm s}^\mathrm{T} . Thus, the dot product of any vector {\boldsymbol{f}} with the stationary vector {\boldsymbol{v}}_{\rm s} is calculated as follows:
\begin{aligned} {\boldsymbol{v}}^\mathrm{T}_{\rm s} \cdot {\boldsymbol{f}} = D({\boldsymbol{p}},\,{\boldsymbol{q}},\,{\boldsymbol{f}}) = {det} \left( \begin{array}{lllc} p_{\rm 1}q_{\rm 1} - 1 & p_{\rm 1} - 1 & q_{\rm 1} - 1 & f_{\rm 1} \\ p_{\rm 2}q_{\rm 2} & p_{\rm 2} - 1 & q_{\rm 2} & f_2 \\ p_{\rm 3}q_{\rm 3} & p_{\rm 3} & q_{\rm 3} - 1& f_3\\ p_{\rm 4}q_{\rm 4} & p_{\rm 4} & q_{\rm 4} & f_4 \\ \end{array} \right). \end{aligned} (5) It is clear that the second column of (5) consists of the elements of {\boldsymbol{p}} , and can be solely determined by the platform, which is denoted as \tilde{{\boldsymbol{p}}} = (p_{\rm 1} -1,\; p_{\rm 2} -1, p_{\rm 3},\; p_{\rm 4})^\mathrm{T} . Hence, when {\boldsymbol{f}} = \alpha {\boldsymbol{M}}^{\rm e} + \beta {\boldsymbol{M}}^{\rm r} + \gamma {\boldsymbol{1}} , where \alpha and \beta are weight factors, we have {\boldsymbol{v}}^\mathrm{T}_{\rm s} \cdot {\boldsymbol{f}} = {\boldsymbol{v}}^\mathrm{T}_{\rm s} \cdot (\alpha {\boldsymbol{M}}^{\rm e} + \beta {\boldsymbol{M}}^{\rm r} + \gamma {\boldsymbol{1}}) = \alpha U^{\rm e} + \beta U^{\rm r} + \gamma , where \gamma is a scalar, U^{\rm e} and U^{\rm r} are the expected utilities in the final stable state. Based on (5), we also have \alpha U^{\rm{e}}+\beta U^{\rm{r}}+\gamma=D(\boldsymbol{p},\boldsymbol{\ q},\ \alpha\boldsymbol{M}^{\rm{e}}+\beta\boldsymbol{M}^{\rm{r}}+\gamma\boldsymbol{1}). Namely, when \tilde{{\boldsymbol{p}}} = \phi(\alpha {\boldsymbol{M}}^{\rm e} + \beta {\boldsymbol{M}}^{\rm r} + \gamma {\boldsymbol{1}}) (\phi \neq 0) , the second column of the corresponding matrix is proportional to the fourth column. According to the properties of the matrix determinant, we have
\begin{aligned} \alpha U^{\rm e} + \beta U^{\rm r} + \gamma =0. \end{aligned} (6) (6) indicates the expected payoffs have a liner relationship, which is brought by the \tilde{{\boldsymbol{p}}} = \phi(\alpha {\boldsymbol{M}}^{\rm e} + \beta {\boldsymbol{M}}^{\rm r} + \gamma {\boldsymbol{1}}) (\phi \neq 0) . Note that \tilde{{\boldsymbol{p}}} is determined by {\boldsymbol{p}} , and \tilde{{\boldsymbol{p}}} = (p_{\rm 1} -1,\; p_{\rm 2} -1,\; p_{\rm 3},\; p_{\rm 4})^\mathrm{T} . Therefore, the strategy {\boldsymbol{p}} adopted by the platform is known as a ZD-VCS strategy. We define the weighted social welfare of this game as follows:
\begin{aligned} U_{\rm all} = \alpha U^{\rm e} + \beta U^{\rm r} = -\gamma. \end{aligned} (7) The above analysis implies that when the platform adopts the ZD-VCS strategy, the platform has unilateral control over the social welfare at a desired value ( U_{\rm all} =-\gamma ) no matter what strategy the ISP adopts. This provides the platform with a powerful tool to maintain the stability of the total utility. The maximal and stable social welfare that the platform maintains regardless of the ISP’s strategy can be achieved by solving the following problem:
\begin{split} &{\rm max} \quad U_{\rm all} = \alpha U^{\rm e}({\boldsymbol{p}},\ {\boldsymbol{q}}) + \beta U^{\rm r}({\boldsymbol{p}},\ {\boldsymbol{q}}), \quad \forall {\boldsymbol{q}},\\ &{\rm s.t.} \quad \left\{ \begin{array}{lc} {\bf 0}\leqslant {\boldsymbol{p}} \leqslant {\boldsymbol{1}}, \\ \alpha U^{\rm e} + \beta U^{\rm r} + \gamma =0.\\ \end{array} \right. \end{split} U^{\rm{e}}(\boldsymbol{p},\boldsymbol{\ q}) and U^{\rm{r}}(\boldsymbol{p},\boldsymbol{\ q}) refer to the expected payoffs of the platform and the ISP, which are determined by {\boldsymbol{p}} and {\boldsymbol{q}} . Accordingly, the problem is equivalent to solving the following problem:
\begin{split} &{\rm min} \quad \gamma,\\ &{\rm s.t.} \quad \left\{ \begin{array}{lc} {\bf 0}\leqslant {\boldsymbol{p}} \leqslant {\boldsymbol{1}}, \\ \tilde{{\boldsymbol{p}}} = \phi(\alpha {\boldsymbol{M}}^{\rm e} + \beta {\boldsymbol{M}}^{\rm r} + \gamma {\boldsymbol{1}}),\\ \phi\neq 0.\\ \end{array} \right. \end{split} (8) Next, we discuss how to calculate each element of {\boldsymbol{p}} . Specifically, we divide the discussion by \phi > 0 and \phi < 0 , respectively. \phi is a scaling coefficient that controls the convergence rate to the stable state.
When \phi is positive, we put the constraint {\boldsymbol{p}} \geqslant 0 into the second constraint of (8), and get
\begin{split} &\gamma_{\rm min} = {\rm max}(\tau_{i}), \quad \forall i \in \{1,\;2,\;3,\;4\},\;\\ &\tau_{i}= \left\{ \begin{array}{lc} - \alpha m^{\rm e}_{i}- \beta m^{\rm r}_{i}-1/\phi,\; &\quad i =1,\;2,\; \\ -\alpha m^{\rm e}_{i} -\beta m^{\rm r}_{i},\;&\quad i = 3,\;4. \\ \end{array} \right. \end{split} (9) Correspondingly, we put the constraint {\boldsymbol{p}} \leqslant 1 into the second constraint of (8) and obtain
\begin{split} &\gamma_{\rm max} = {\rm min}(\tau_{j}), \quad \forall j \in \{5,\;6,\;7,\;8\},\;\\ &\tau_{j} = \tau_{i+4}= \left\{ \begin{array}{lc} -\alpha m^{\rm e}_{i} -\beta m^{\rm r}_{i},\; &\quad i =1,\;2,\; \\ \nonumber - \alpha m^{\rm e}_{i}- \beta m^{\rm r}_{i}+1/\phi, &\quad i = 3,\;4,\; \\ \end{array} \right. \end{split} where \phi is a positive value that normalizes {\boldsymbol{p}} in the range [0,\; 1] . Note that \gamma is feasible only when it satisfies \gamma_{\rm min} \leqslant \gamma_{\rm max} .
Similarly, when \phi is negative and normalizes {\boldsymbol{p}} in the range [0,\; 1] , considering the constraint {\boldsymbol{p}} \geqslant 0 , we have
\begin{aligned} \gamma_{\rm min} = {\rm max}(\tau_{j}),\; \forall j \in \{5,\;6,\;7,\;8\}. \end{aligned} (10) While considering {\boldsymbol{p}} \leqslant 1 , we have \gamma_{\rm max} = {\rm min}(\tau_{i}), \forall i \in \{1,\;2,\;3,\;4\} . Therefore, \gamma is feasible when \gamma_{\rm min} \leqslant \gamma_{\rm max} , and that is {\rm max}(\tau_{j}) \leqslant {\rm min}(\tau_{i}), \forall i \in \{1,\;2, 3,\;4\},\; \forall j \in \{5,\;6,\;7,\;8\} .
According to (9) and (10), when \gamma reaches \gamma_{\rm min} , each element of {\boldsymbol{p}} is represented as follows:
\begin{split} &p_{i} =\left\{ \begin{array}{lc} \phi(\alpha m^{\rm e}_{i}+ \beta m^{\rm r}_{i} + \gamma_{\rm min}) +1,\; & i =1,\;2,\; \\\phi(\alpha m^{\rm e}_{i}+ \beta m^{\rm r}_{i} + \gamma_{\rm min}),\; & i = 3,\;4. \\\end{array} \right. \end{split} (11) Thus, the ZD-VCS strategy {\boldsymbol{p}} of the platform meets \tilde{{\boldsymbol{p}}} = \phi(\alpha {\boldsymbol{M}}^{\rm e} + \beta {\boldsymbol{M}}^{\rm r} + \gamma {\boldsymbol{1}}) (\phi \neq 0) .
We take the payoff matrices in Fig.4 as an example, where {\boldsymbol{M}}^{\rm e} = (m^{\rm e}_{1},\; m^{\rm e}_{2},\;m^{\rm e}_{3},\;m^{\rm e}_{4}) = (30,\; 20,\; 18,\; 16) and {\boldsymbol{M}}^{\rm r} = (m^{\rm r}_{1} , m^{\rm r}_{2} , m^{\rm r}_{3} , m^{\rm r}_{4}) = (21,\; 28,\; 10,\; 22) . If we set \phi = -0. 05 and \alpha = \beta = 1 , then \gamma_{\rm min} = (-51,\; -48, -28-20,\; -38-20) = -48 , and \gamma_{\rm max} = (-51+20, -48+20,\; -28,\; -38) = -28 . Therefore \gamma_{\rm min} < \gamma_{\rm max} is feasible when \phi = -0. 05 . Note that \phi is set to guarantee each element in {\boldsymbol{p}} is in the range of [0,\; 1] . According to (11), p_{1} = -0.05(51-48) +1 = 0.85,\; p_{2} = -0.05(48-48) +1 = 0,\; p_{3} = -0.05(28-48) =1 , and p_{4} = -0.05(38-48) = 0.5 . Thus, the ZD-VCS strategy is represented as {\boldsymbol{p}} = (0.85,\; 0,\; 1,\; 0.5) . When {\boldsymbol{p}} is adopted by the platform in the iterated game, the social welfare can achieve a stable and maximal value -\gamma_{\rm min} =48 .
5.3 ZD-VCS Strategy in the Continuous Model
In this subsection, we further analyze the social welfare control problem in the continuous case. Then, we discuss how to obtain the ZD-VCS strategy in the continuous case when we aim to maintain the maximal stable total expected payoff.
To further analyze the social welfare control problem, we consider the ZD-VCS strategy in the continuous case. Based on the number of sensing tasks x_{\rm e} and the candidate available RSUs x_{\rm r} , we fit the continuous payoff functions F_{\rm g}(x_{\rm e}, \; x_{\rm r}) and F_{\rm t}(x_{\rm e}, \; x_{\rm r}) for the platform and the ISP, respectively, where the fixed x_{\rm e} and x_{\rm r} correspond to the fixed actions. We assume that both the platform and the ISP choose their actions according to the outcomes of the previous round. Similarly, we define the mixed strategy of the platform p(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm e}) as the conditional probability to choose the action x_{\rm e} in the current round when the state in the previous round is x'_{\rm e} x'_{\rm r} , where x'_{\rm e}, \; x_{\rm e} \in [l^{\rm e}, \; h^{\rm e}] and x'_{\rm r}, \; x_{\rm r} \in [l^{\rm r}, \; h^{\rm r}] . Since x_{\rm e} can be any value in the continuous domain in mathematical analysis, we have \int\nolimits^{h^{\rm e}}_{l^{\rm e}} p(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm e}) {\rm d} x_{\rm e} = 1 . In addition, the ISP’s mixed strategy q(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm r}) also refers to the conditional probability that the ISP adopts action x_{\rm r} when the state in the previous round is x'_{\rm e} x'_{\rm r} . The mixed strategy q(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm r}) satisfies \int\nolimits^{h^{\rm r}}_{l^{\rm r}} q(x'_{\rm e}, x'_{\rm r}, \; x_{\rm r}) {\rm d} x_{\rm r} = 1 .
Next, we denote the joint probability for the platform and the ISP to choose x_{\rm e} and x_{\rm r} in each round by v(x_{\rm e}, \; x_{\rm r}) . Considering the payoff functions F_{\rm g}(x_{\rm e}, \; x_{\rm r}) and F_{\rm t}(x_{\rm e}, \; x_{\rm r}) , we obtain the expected utilities of the platform and the ISP in the current round as: U^{\rm e} = \int\nolimits^{h^{{\rm r}}}_{l^{{\rm r}}}\int\nolimits^{h^{{\rm e}}}_{l^{{\rm e}}}v(x_{\rm e}, \; x_{\rm r})F_{\rm g}(x_{\rm e}, \; x_{\rm r}){\rm d} x_{\rm e} {\rm d}x_{\rm r} , and U^{\rm r} = \int\nolimits^{h^{{\rm r}}}_{l^{{\rm r}}} \int\nolimits^{h^{{\rm e}}}_{l^{{\rm e}}}v(x_{\rm e}, x_{\rm r})F_{\rm t}(x_{\rm e}, \; x_{\rm r}){\rm d} x_{\rm e} {\rm d}x_{\rm r} , respectively. Furthermore, similar to the state transition matrix {\boldsymbol{H}} in the discrete model, we denote a transition function H(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm e}, \; x_{\rm r}) , indicating the state transition probability from state x'_{\rm e} x'_{\rm r} in the previous round to state x_{\rm e} x_{\rm r} in the current round, which is expressed as H(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm e}, \; x_{\rm r}) = p(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm e})q(x'_{\rm e},\; x'_{\rm r}, \; x_{\rm r}). Then, the relationship of the state probabilities in two sequential rounds is denoted as v(x'_{\rm e},\; x'_{\rm r})H(x'_{\rm e},\; x'_{\rm r},\; x_{\rm e}, x_{\rm r}) = v(x_{\rm e}, \; x_{\rm r}).
We denote the stationary state as v^{\rm s}(x_{\rm e}, \; x_{\rm r}) . The iterated game reaches a stable state when v(x'_{\rm e},\; x'_{\rm r}) = v(x_{\rm e}, \; x_{\rm r}) = v^{\rm s}(x_{\rm e}, \; x_{\rm r}) . Thus, we have the following theorem.
Theorem 3. When the platform’s strategy p(x'_{\rm e},\; x'_{\rm r}, x_{\rm e}) satisfies \tilde{p}(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = \phi(\alpha F_{\rm g}(x_{\rm e}, \; x_{\rm r}) + \beta F_{\rm t}(x_{\rm e},\ x_{\rm r}) + \gamma) (\phi \neq 0) , the platform’s expected utility U^{\rm e} and the ISP’s expected utility U^{\rm r} satisfy the following relationship: \alpha U^{\rm e} + \beta U^{\rm r} + \gamma = 0, where the function \tilde{p}(x'_{\rm e},\; x'_{\rm r}, h^{\rm e}) is defined as
\begin{split} &\tilde{p}(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = \left\{ \begin{array}{lc} p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}), &\quad {\rm if}\;\; x'_{\rm e}< h^{\rm e},\\ p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) - 1, &\quad {\rm if}\;\; x'_{\rm e}= h^{\rm e}. \\ \end{array} \right. \end{split} Next, we discuss how to obtain the function p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) , which is the continuous ZD-VCS strategy.
The weighted social welfare is defined as U_{\rm all} = \alpha U^{\rm e} + \beta U^{\rm r} = -\gamma . According to Theorem 3, the platform’s strategy p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) is the only factor affecting U_{\rm all} , which is viewed as the ZD-VCS strategy in the continuous case. Specifically, the platform can solve the following optimization problem to achieve unilateral control of social welfare:
\begin{split} &{\rm max} \quad U_{\rm all} = \alpha U^{\rm e}({\boldsymbol{p}},\ {\boldsymbol{q}}) + \beta U^{\rm r}({\boldsymbol{p}},\ {\boldsymbol{q}}), \quad \forall {\boldsymbol{q}},\\ &{\rm s.t.} \quad \left\{ \begin{array}{lc} {\boldsymbol{0}}\leqslant {\boldsymbol{p}} \leqslant {\boldsymbol{1}}, \\ \alpha U^{\rm e} + \beta U^{\rm r} + \gamma =0.\\ \end{array} \right. \end{split} (12) To simply illustrate the following discussion, we denote T(x_{\rm e}, \; x_{\rm r}) = \alpha F_{\rm g}(x_{\rm e}, \; x_{\rm r}) + \beta F_{\rm t}(x_{\rm e}, \; x_{\rm r}) . Then (12) is converted into
\begin{split} &{\rm min} \quad \gamma,\\ &{\rm s.t.} \quad \left\{ \begin{array}{lc} 0\leqslant p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) \leqslant 1, \\ \tilde{p}(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e})=\phi(T(x_{\rm e}, \; x_{\rm r}) + \gamma),\\ \phi \neq 0.\\ \end{array} \right. \end{split} In order to obtain the function p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) , we divide the discussion by \phi > 0 and \phi < 0 , respectively.
When \phi is positive and constraint p\geqslant 0 , we obtain
\begin{split} &\gamma_{\rm min} = {\rm max}(\tau(x'_{\rm e},\; x'_{\rm r})), \quad \forall x'_{\rm e} \in [l^{\rm e}, \ h^{\rm e}],\ \forall x'_{\rm r} \in [l^{\rm r}, \; h^{\rm r}],\\ &\tau(x'_{\rm e},\; x'_{\rm r}) =\left\{ \begin{array}{lc} -T(x'_{\rm e},\; x'_{\rm r}), &\quad {\rm if}\;\; x'_{\rm e}< h^{\rm e},\\ -T(x'_{\rm e},\; x'_{\rm r}) - 1/\phi, &\quad {\rm if}\;\; x'_{\rm e}= h^{\rm e}. \\ \end{array} \right. \end{split} While considering the constraint condition p\leqslant 1 , we obtain
\begin{split} &\gamma_{\rm max} = {\rm min}(\tau(x''_{\rm e},\; x''_{\rm r})), \quad \forall x''_{\rm e} \in [l^{\rm e}, \; h^{\rm e}],\ \forall x''_{\rm r} \in [l^{\rm r}, \; h^{\rm r}],\\ &\tau(x''_{\rm e},\; x''_{\rm r}) =\left\{ \begin{array}{lc} 1/\phi-T(x''_{\rm e},\; x''_{\rm r}), &\quad {\rm if}\;\; x''_{\rm e}< h^{\rm e},\\ \nonumber -T(x''_{\rm e},\; x''_{\rm r}), &\quad {\rm if}\;\; x''_{\rm e}= h^{\rm e}. \\ \end{array} \right. \end{split} \gamma is feasible when \gamma_{\rm min} < \gamma_{\rm max} . That is {\rm max}(\tau(x'_{\rm e}, x'_{\rm r})) <{\rm min}(\tau(x''_{\rm e},\, x''_{\rm r})),\, \forall x'_{\rm e},\, x''_{\rm e} \in [l^{\rm e}, \, h^{\rm e}],\; \forall x'_{\rm r},\, x''_{\rm r} \in [l^{\rm r},\,h^{\rm r}] . Since \phi is a positive value that normalizes {\boldsymbol{p}} in the range [0, \;1] , we get the minimum value of \gamma :
\begin{aligned} \gamma_{\rm min} = {\rm max}(-T(x'_{\rm e},\; x'_{\rm r})), \ \forall x'_{\rm e} \in [l^{\rm e}, \; h^{\rm e}), \;\forall x'_{\rm r} \in [l^{\rm r}, \; h^{\rm r}]. \end{aligned} (13) When \phi is negative, considering the constraint p \geqslant 0 , we obtain \gamma_{\rm max} = {\rm min}(\tau(x'_{\rm e},\; x'_{\rm r})), \;\forall x'_{\rm e} \in [l^{\rm e}, \; h^{\rm e}], \forall x'_{\rm r} \in [l^{\rm r}, \; h^{\rm r}] . When considering p \leqslant 1 , we have \gamma_{\rm min} = {\rm max}(\tau(x''_{\rm e},\ x''_{\rm r}), \forall x''_{\rm e} \in [l^{\rm e}, \ h^{\rm e}], \ \forall x''_{\rm r} \in [l^{\rm r}, \ h^{\rm r}] . Then, \gamma is feasible only when \gamma_{\rm min} < \gamma_{\rm max} , i.e., {\rm max}(\tau(x''_{\rm e}, \; x''_{\rm r})) < {\rm min}(\tau(x'_{\rm e},\; x'_{\rm r})) . That is {\rm max}(-T(x''_{\rm e},\; x''_{\rm r})) < {\rm min}(-T(x'_{\rm e}, x'_{\rm r})) , \forall x'_{\rm e},x''_{\rm e} \in [l^{\rm e}, \ h^{\rm e}],\ \forall x'_{\rm r},\ x''_{\rm r} \in [l^{\rm r}, \ h^{\rm r}] . Thus, we have the following result:
\begin{split} & \gamma_{\rm min} = {\rm max}(\tau(x''_{\rm e},\; x''_{\rm r})) = {\rm max}(-T(x''_{\rm e},\; x''_{\rm r})), \\ &\forall x''_{\rm e}=h^{\rm e}, \forall x''_{\rm r} \in [l^{\rm r}, \; h^{\rm r}]. \end{split} (14) Therefore, according to (13) and (14), the platform’s continuous ZD-VCS strategy is computed as follows:
\begin{split} &p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = \left\{ \begin{array}{lc} \phi(T(x'_{\rm e},\; x'_{\rm r}) + \gamma_{\rm min}), &\,{\rm if}\;\; x'_{\rm e} < h^{\rm e}, \\ \phi(T(x'_{\rm e},\; x'_{\rm r}) + \gamma_{\rm min})+1, &\, {\rm if}\;\; x'_{\rm e} = h^{\rm e}. \\ \end{array} \right. \end{split} (15) We illustrate how to obtain the wise-function through a simple example. We set \phi < 0, \;\alpha = \beta = 1 , x_{\rm e} \in [1,\;10] \ ( h^{\rm e} = 10) and x_{\rm r} \in [1,\; 10] , then F_{\rm g}(x_{\rm e}, \; x_{\rm r}) = 6x_{\rm r}-x_{\rm e} , and F_{\rm t}(x_{\rm e}, \; x_{\rm r}) =3x_{\rm e}- 6x_{\rm r} . According to the previous discussion, we obtain T(x_{\rm e}, \; x_{\rm r}) = F_{\rm g}(x_{\rm e}, x_{\rm r}) + F_{\rm t}(x_{\rm e}, x_{\rm r}) = 2x_{\rm e} . In the case of \phi < 0 , \gamma_{\rm min} ={\rm max} (\tau(x''_{\rm e},\; x''_{\rm r})) = {\rm max}( -T(x''_{\rm e},\; x''_{\rm r})) = {\rm max}(-2x''_{\rm e}) , where x''_{\rm e} =h^{\rm e} = 10 . Therefore \gamma_{\rm min} = {\rm max}(-2 \times 10) = -20 . \gamma_{\rm max} = {\rm min}(\tau(x'_{\rm e},\; x'_{\rm r})) = {\rm max}(-2x'_{\rm e}) , where x_{\rm e} \in [1,\; 10] , therefore \gamma_{\rm max} = -2 \times 1 = -2 . Thus, \gamma_{\rm min} <\gamma_{\rm max} . According to (15), the ZD-VCS strategy p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) in the continuous case is represented as follows:
\begin{split} &p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = \left\{ \begin{array}{ll} \phi(2x_{\rm e} - 20), & {\rm if}\;\; x'_{\rm e} \in [1, 10), \\ \nonumber \phi(2x_{\rm e} - 20) + 1 = 1, & {\rm if}\;\; x'_{\rm e} = 10. \\ \end{array} \right. \end{split} Note that we need to choose proper \phi <0 to satisfy 0 \leqslant p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) \leqslant 1 . Since 0\leqslant \phi(2x_{\rm e}'-20) \leqslant 1 , we can obtain ({2x_{\rm e}' - 20})^{-1}\leqslant \phi <0,\; 1 ( \leqslant x'_{\rm e} <10) . Therefore, parameter \phi is chosen as ({2x_{\rm e}' -20})^{-1} \leqslant \phi <0 to guarantee 0\leqslant p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) \leqslant 1 . In the iterated game, when the platform adopts the pre-calculated p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) in the continuous case, the social welfare can be unilaterally controlled at a maximal and stable value -\gamma_{\rm min} =20 in the long term.
In sum, in the continuous case, the ZD-VCS strategy adopted by the platform is a piece-wise function, as shown in (15). No matter what the strategy of the ISP is, the social welfare can be unilaterally maintained at the value -\gamma_{\rm min} .
5.4 Extension: Extortion Strategy
Based on (6), a special kind of zero-determinant strategies, the extortion strategy, is derived. Below we discuss how the extortion strategy is derived, and how it is used in the iterated vehicular crowdsensing game.
When the platform is in a dominant role and wants to control its and its opponent’s payoffs at a predefined ratio in some scenarios, for the purpose of unilateral control, we can help the platform to extortionately control the payoff of the opponent at a low value. Thus, we propose the extortion strategy in the discrete model for the platform, which is a kind of zero-determinant strategies with special parameter settings, and the details are as follows.
In the case that the platform attempts to enforce an extortionate share of payoffs larger than the mutual noncooperation value, based on (6), when \tilde{{\boldsymbol{p}}} = \phi(({\boldsymbol{M}}^{\rm e} - m_{4}^{\rm e}{\boldsymbol{1}}) - \chi({\boldsymbol{M}}^{\rm r} - m_{4}^{\rm r}{\boldsymbol{1}})) , \alpha = \phi , and \beta = -\phi\chi ( \phi \neq 0 ), that is, \chi = -{\beta}/{\alpha} , \gamma = \phi(\chi m_{4}^{\rm r} - m_{4}^{\rm e}) . Then the linear relationship between the expected payoff of the platform and that of the ISP is obtained, and (U^{\rm e} - m_{4}^{\rm e}) = \chi(U^{\rm r} - m_{4}^{\rm r}) , where \chi \geqslant 1 is called the extortion ratio and \phi is employed to guarantee that each element in {\boldsymbol{p}} is in the range of [0, \;1] . The specific extortion strategy of the platform can be obtained by solving the following equations:
\begin{split} \left\{ \begin{array}{lc} p_{\rm 1} = 1 + \phi((m_{1}^{\rm e} - m_{4}^{\rm e}) -\chi(m_{1}^{\rm r} - m_{4}^{\rm r})), \\ p_{\rm 2} = 1 + \phi((m_{2}^{\rm e} - m_{4}^{\rm e}) -\chi(m_{2}^{\rm r} - m_{4}^{\rm r})),\\ p_{\rm 3} = \phi((m_{3}^{\rm e} - m_{4}^{\rm e}) -\chi(m_{3}^{\rm r} - m_{4}^{\rm r})),\\ p_{\rm 4} = 0.\\ \end{array} \right. \end{split} Obviously, the feasible solution exists and is determined by any \chi and a sufficiently small \phi . Specifically, to ensure that each element of {\boldsymbol{p}} belongs to [0, \;1] , \phi should satisfy: \phi \in (0, \;\tilde{\phi}_{1}] when \phi > 0 , and \phi \in [\tilde{\phi}_{2},\; 0 ) when \phi < 0 , where \tilde{\phi}_{1} = {\rm min}\{\pi_{1},\;\pi_{2},\;\pi_{3}\} , \tilde{\phi}_{2} = {\rm max}\{\pi_{1},\;\pi_{2},\;\pi_{3}\} . For convenience, we set
\begin{split} &\pi_{1} = \frac{-1}{(m_{1}^{\rm e} - m_{4}^{\rm e}) -\chi(m_{1}^{\rm r} - m_{4}^{\rm r})},\\ &\pi_{2} = \frac{-1}{(m_{2}^{\rm e} - m_{4}^{\rm e}) -\chi(m_{2}^{\rm r} - m_{4}^{\rm r})},\\ &\pi_{3} = \frac{1}{(m_{3}^{\rm e} - m_{4}^{\rm e}) -\chi(m_{3}^{\rm r} - m_{4}^{\rm r})}. \\ \end{split} When the ISP always takes the action of defection, that is {\boldsymbol{q}} = (0,\; 0,\; 0,\; 0) , the minimum utility of ISP is m_{4}^{\rm r} . While ISP unconditionally cooperates, that is {\boldsymbol{q}} = (1,\; 1,\; 1,\; 1) , according to (5), the maximum utility of the ISP can be calculated as
\begin{aligned} \nonumber {\rm min}\,\; U^{\rm r}|_{{\boldsymbol{q}} = (1,\; 1,\; 1,\; 1)} = \frac{D({\boldsymbol{p}},\; {\boldsymbol{q}},\; {\boldsymbol{M}}^{\rm r})}{D({\boldsymbol{p}},\;{\boldsymbol{q}},\;{\boldsymbol{1}})}. \end{aligned} Furthermore, when \chi = 1 , there is no extortion of the platform to the ISP, and thus the maximum utility of the platform can be obtained by (5), and be calculated as follows:
\begin{aligned} \nonumber {\rm max} \,\; U^{\rm r}|_{{\boldsymbol{q}} =(1,\; 1,\; 1,\; 1),\; \chi =1} =\frac{D({\boldsymbol{p}},\; {\boldsymbol{q}},\; {\boldsymbol{M}}^{\rm r})}{D({\boldsymbol{p}},\;{\boldsymbol{q}},\;{\boldsymbol{1}})}. \end{aligned} 6. Performance Evaluation
In this section, we first introduce the experimental setup. Then, we present the experimental results.
6.1 Experimental Setup
We perform experiments on the Taxi-Roma dataset
9 . The dataset includes the GPS coordinates of 320 taxi drivers that work in the center of Rome. These GPS coordinates are collected over 30 days. The dataset is preprocessed by filtering out some outliers. We implement the proposed strategy with real trace-driven simulations. The communication in the physical layer is assumed to be stable and reliable[24]. The traces cover an area with a range of 66 km × 59 km, and we divide the area into 10 \times 10 grids. We assume each RSU in the grid serves as a gateway and each grid is viewed as an area with a sensing task. We calculate the priority of the sensing tasks and RSUs by the number of GPS coordinates in the grid, and both top x_{\rm e} sensing tasks and top x_{\rm r} RSUs are selected by their priorities. From the analysis of traces, we obtain the average task-RSU weighted traffic matrix. Each element in the matrix is the number of sensing data uploaded to an RSU for a task. In the discrete model, we set the lowest and the highest numbers of sensing tasks and RSUs as 2 and 8 , respectively. That is l^{\rm e} = l^{\rm r} = 2 , and h^{\rm e} = h^{\rm r} = 8 . The parameters are set as u_{\rm d} = 30,\; u_{\rm t} = 1,\; u_e = 0.01,\; u_r = 50 , and C = 500 . We discuss how to implement the ZD-VCS strategy in Subsection 6.5 when task-RSU weighted traffic matrix varies on each day. We implement the ZD-VCS strategy based schemes in Python 3.8. All experiments are conducted on a computer with Intel Core i7-6700 CPU and 8G RAM.6.2 Comparison Methods
We describe the following baselines for comparison.
1) ALLC[12, 14, 29]. It is an all cooperation strategy {\boldsymbol{p}} = (1,\; 1,\; 1,\; 1) , which means whatever the opponent player has done in the previous round, it always chooses cooperation.
2) ALLD[12, 29]. It is an all defection strategy {\boldsymbol{p}} = (0,\; 0,\; 0,\; 0) , which means whatever the opponent player has done in the previous round, it always chooses defection.
3) Random[12, 14, 29]. It is an all-random strategy, that is {\boldsymbol{p}} = (0.5,\; 0.5,\; 0.5,\; 0.5) , which means whatever the opponent player has done in the previous round, it randomly chooses cooperation.
4) TFT (Tit-for-Tat)[46, 47]. A TFT player cooperates in the first round and then does what the opponent player has done in the previous round.
5) Evolved[15, 23]. It is an evolved strategy that an evolutionary player starts his/her strategy {\boldsymbol{q}} = (0,\; 0,\; 0,\; 0) , and his/her opponent adopts the ZD-VCS strategy in the iterated game. {\boldsymbol{q}} is updated in each iteration and will be stable at the end of the iterations. The process of calculating the evolved strategy is shown in Algorithm 2.
6) Pavlov (Win-Stay-Lose-Shift Strategy)[47, 48]. If a Pavlov player receives a higher payoff, it will repeat the same action in the next round, which is “win-stay”. If a Pavlov player receives a lower payoff, it will switch to the opposite action, which is “lose-shift”.
6.3 Performance Evaluation on Social Welfare Control
In this subsection, we evaluate the performance of the proposed ZD-VCS on social welfare control in the discrete and continuous model.
6.3.1 Experiments in the Discrete Model
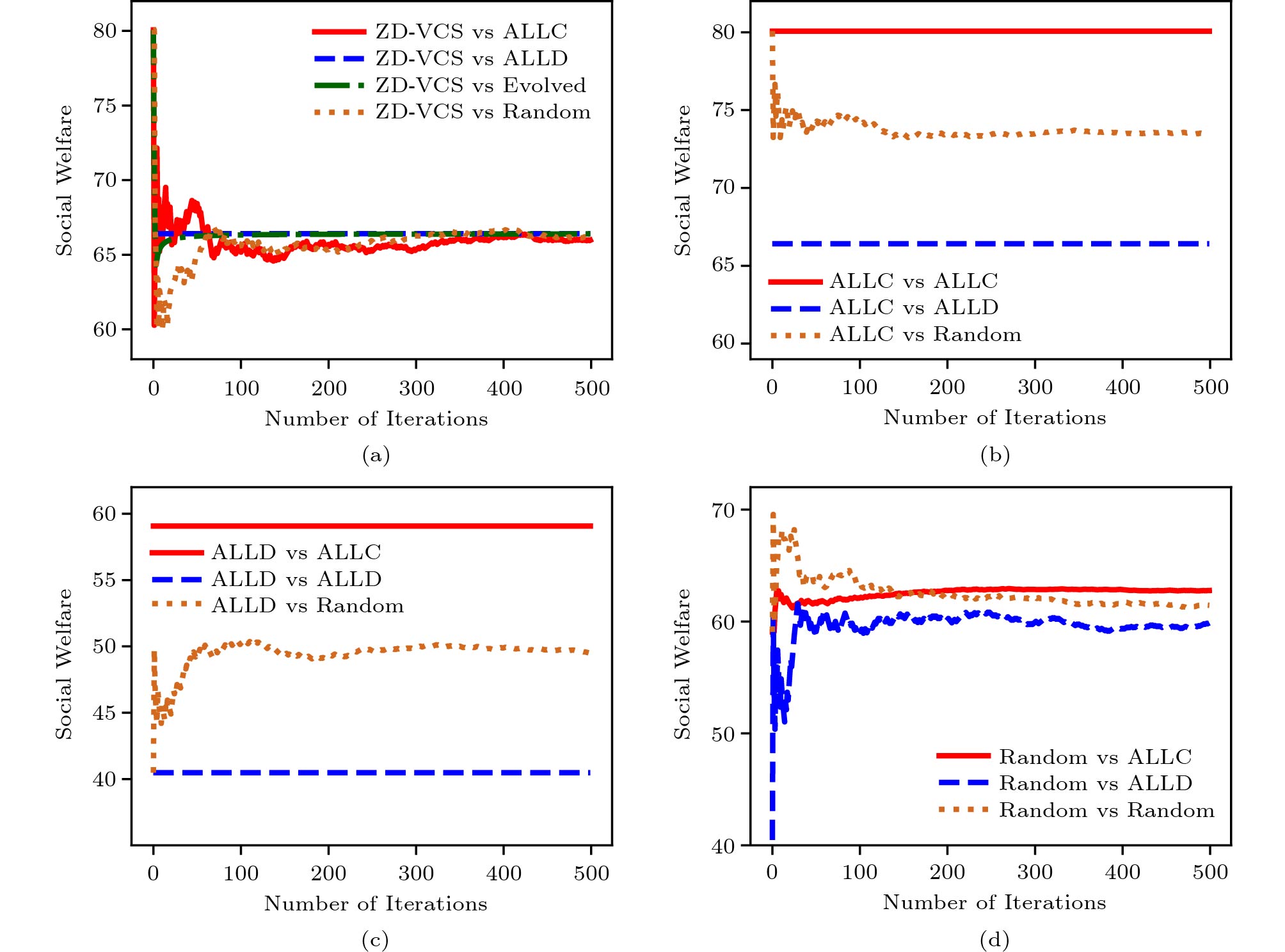
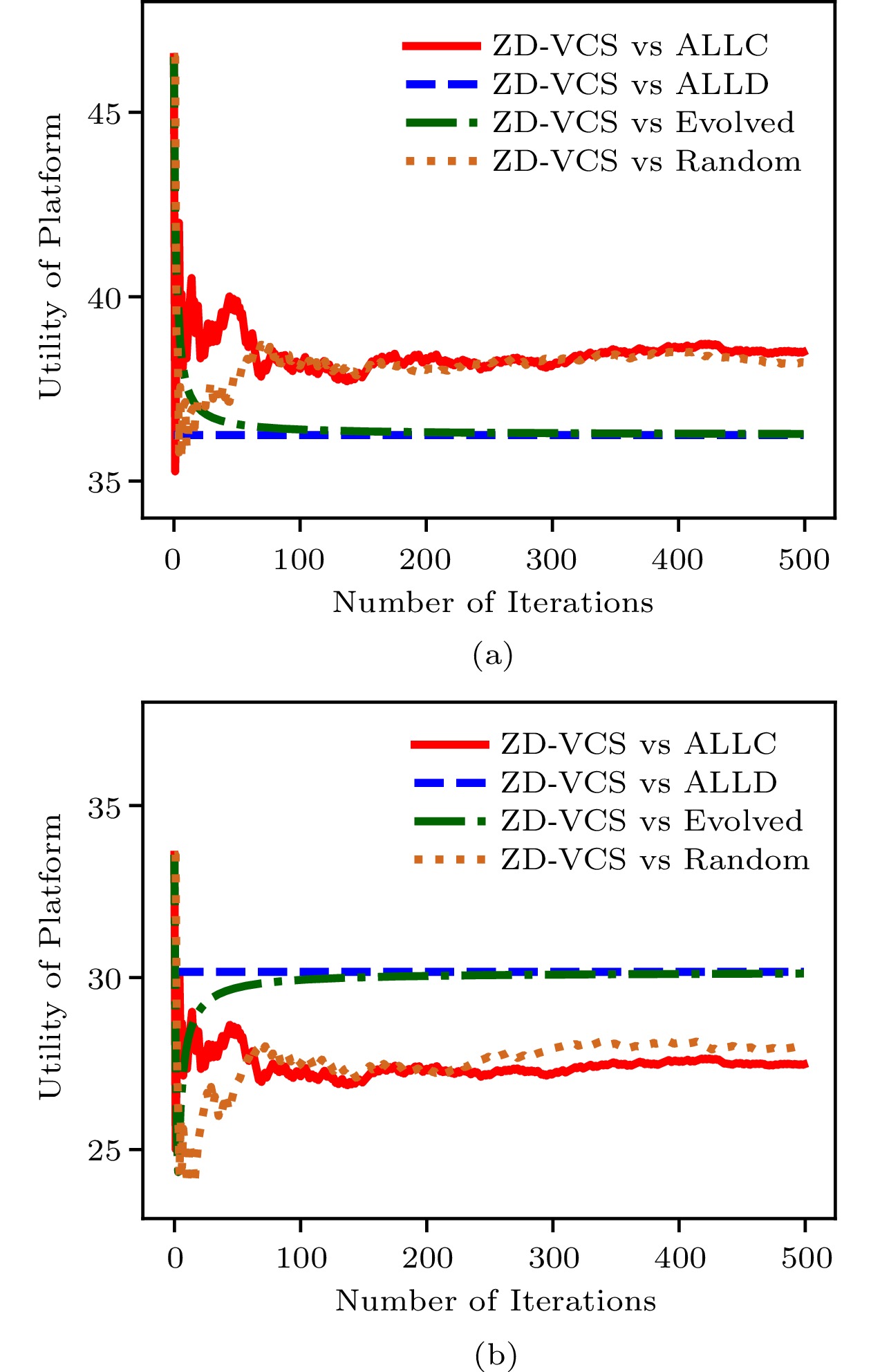
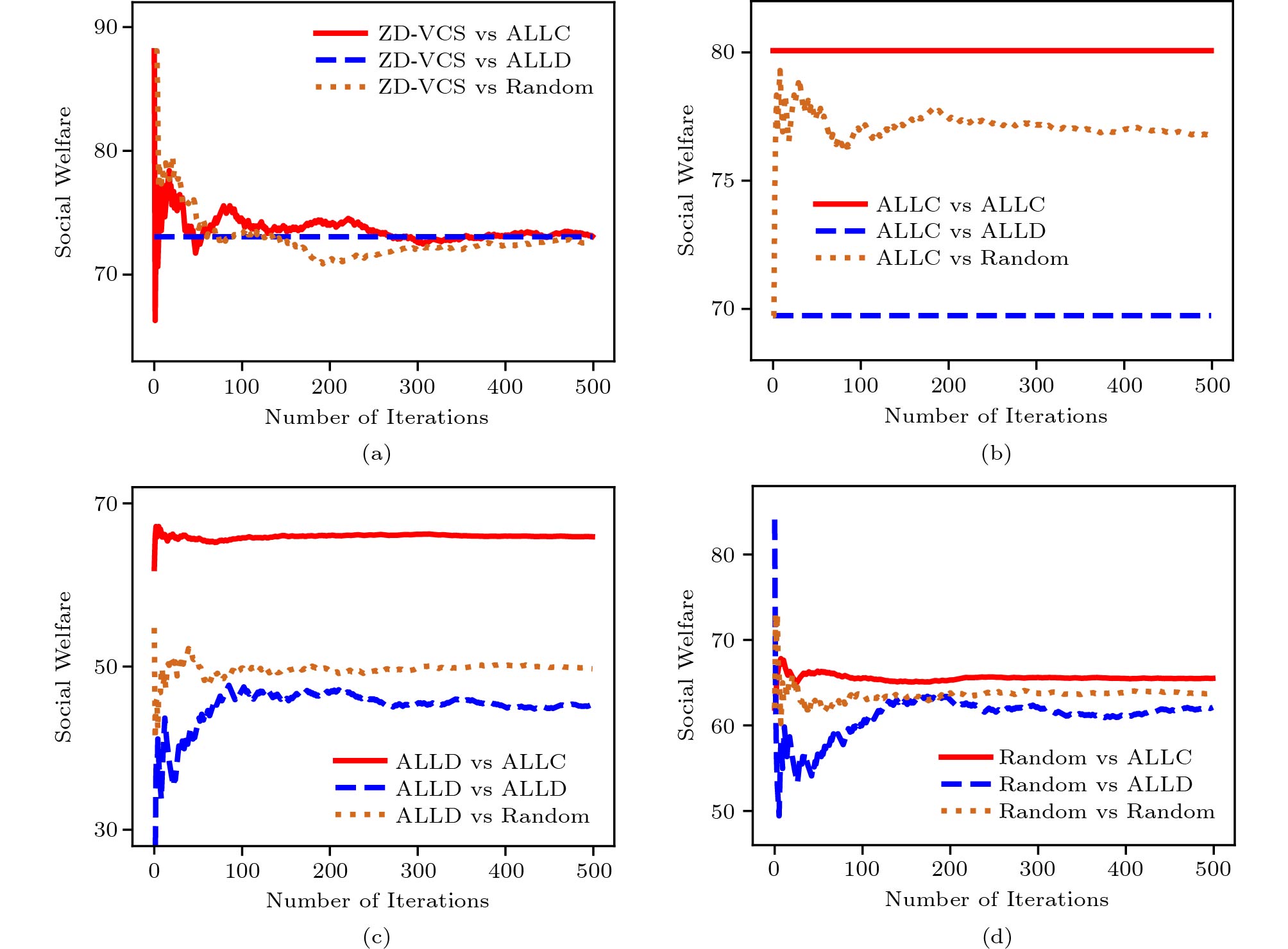
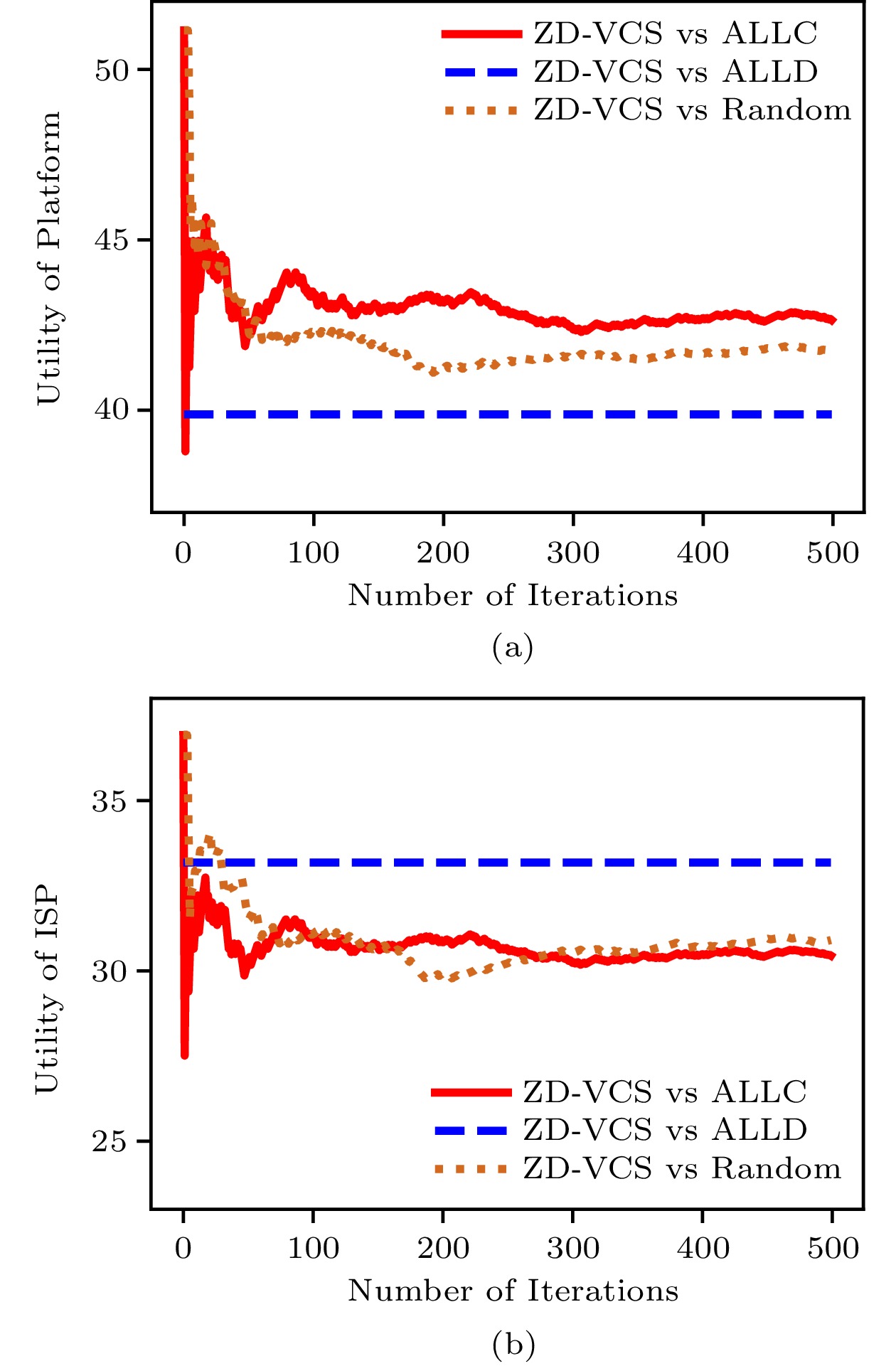
Algorithms 1 and 2 together are the processes of calculating the utilities of the platform and the ISP in the experiment. Considering the general definition of social welfare in (7), we set \alpha = \beta = 1 in social welfare control. In order to evaluate the effectiveness of our proposed scheme, we compare the ZD-VCS strategy with five other classical strategies that might be adopted by the platform. We display the results when the platform adopts the proposed ZD-VCS strategy, all cooperation ( {\boldsymbol{p}} = (1,\; 1,\; 1,\; 1) , denoted as ALLC), all defection ( {\boldsymbol{p}} = (0,\; 0,\; 0,\; 0) , denoted as ALLD), and random ( {\boldsymbol{p}} = (0.5,\; 0.5,\; 0.5,\; 0.5) , denoted as Random) strategies while the ISP adopts three strategies, i.e., ALLC, ALLD, and Random. Furthermore, we also adopt an evolved strategy with the ISP. We view the ISP as an evolutionary player that adopts an evolved strategy. As shown in Fig.5, when the platform adopts the proposed ZD-VCS strategy, whatever the ISP adopts, the social welfare can remain stable and achieve its maximum possible value. However, when the platform takes the other strategies, the social welfare is determined by the strategies of both the platform and the ISP, which indicates that the platform does not dominate the control over the social welfare. In Fig.5(b), when the platform adopts the ALLC strategy, and the ISP adopts the ALLC or Random strategy, the social welfare keeps stable in the long term. But, when the platform adopts ALLC it cannot control social welfare when the ISP adopts a different strategy.
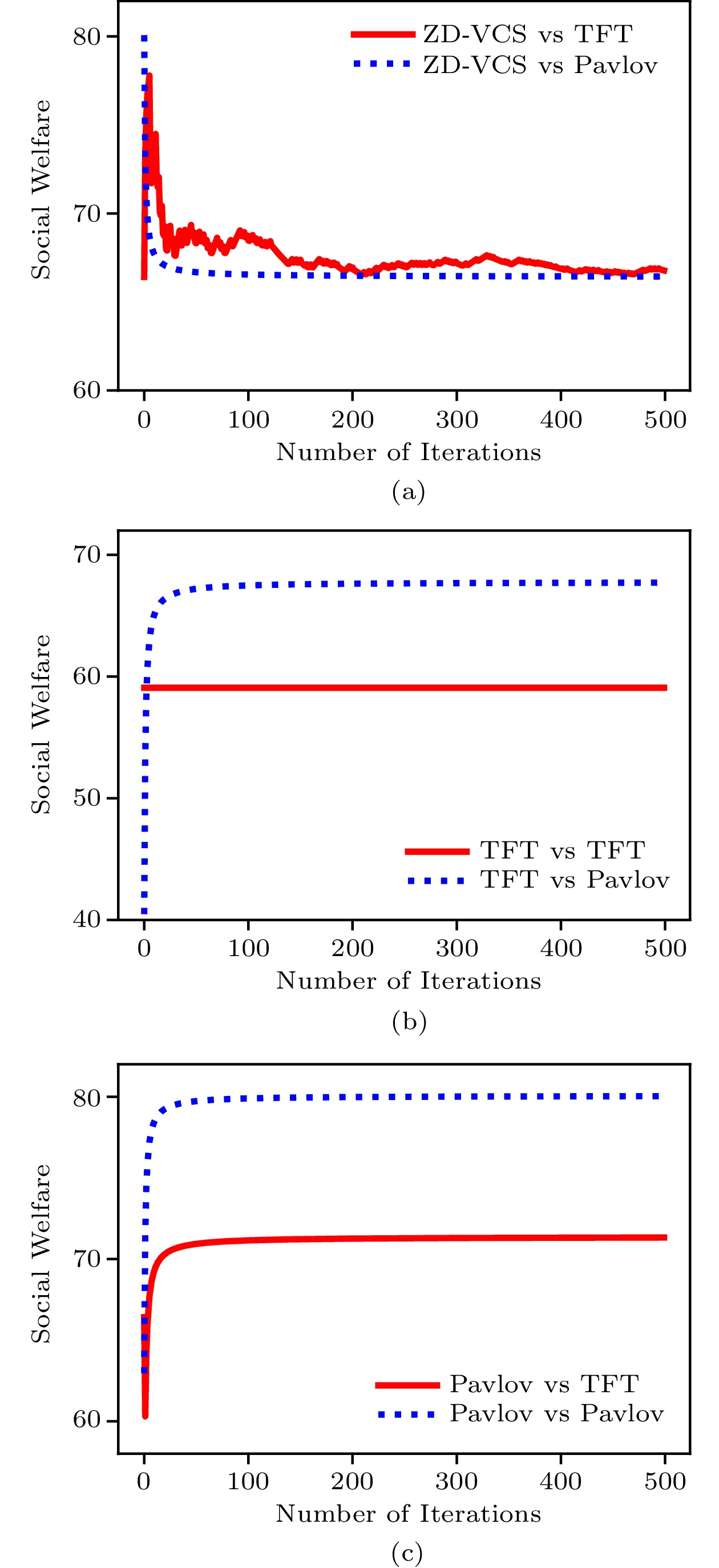
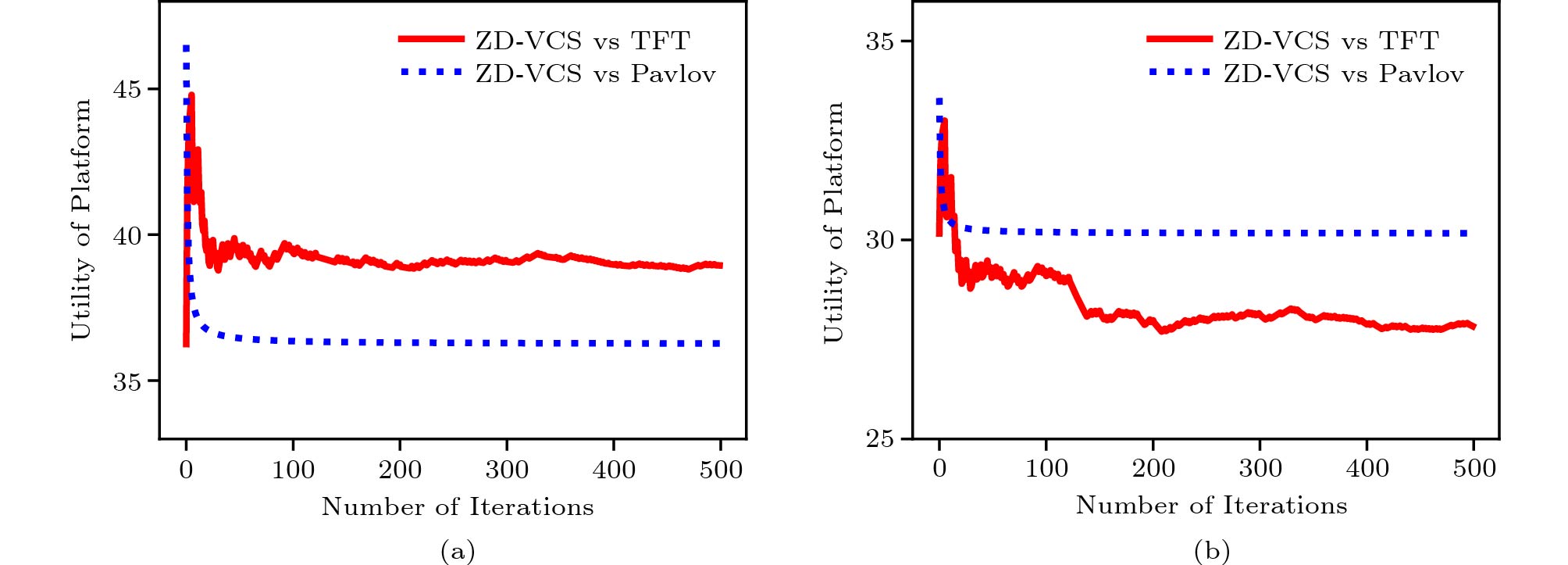
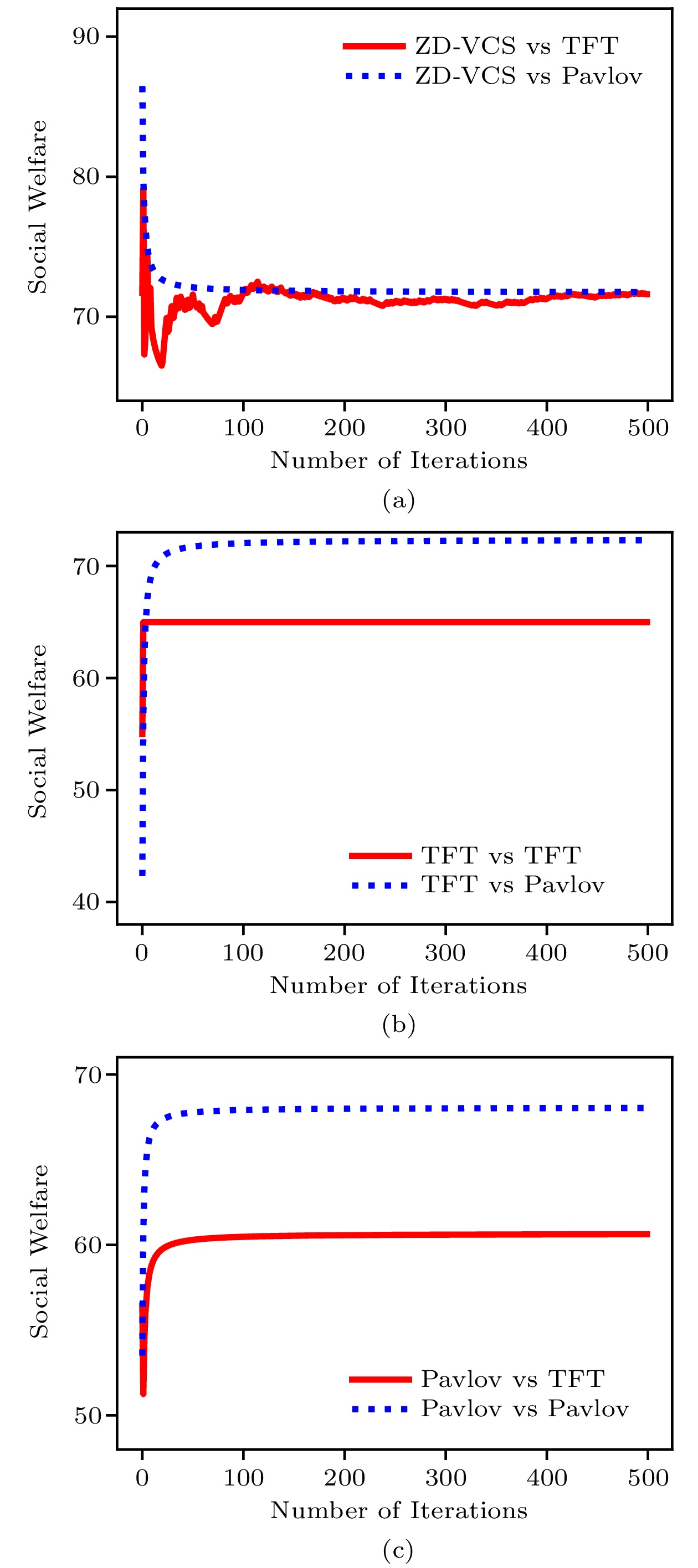
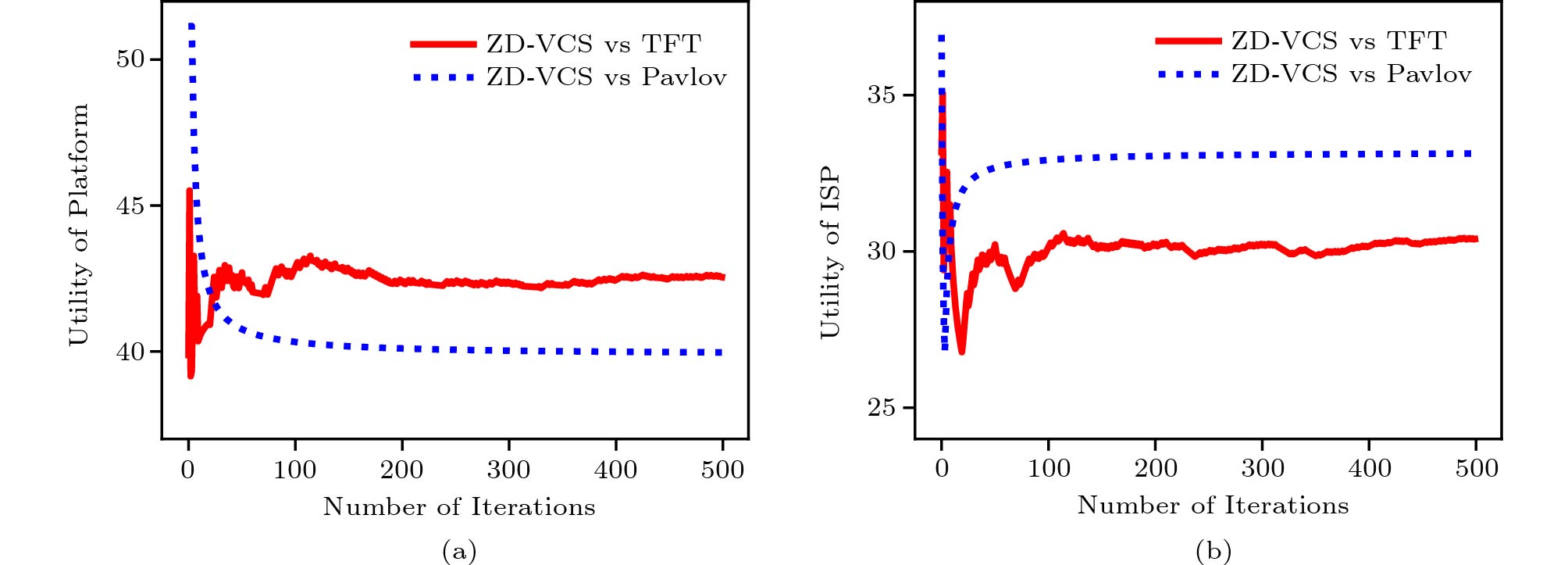
Algorithm 1. ZD-VCS Strategy in the Discrete Model Input: \boldsymbol{p},\;\boldsymbol{q} , x_{\rm r} , previous state x'_{\rm e},\; x'_{\rm r},\;{\boldsymbol{M}}^{\rm e} , number of iterations n Output: U^{\rm e}, \;x'_{\rm e} 1 for i=1;\ i \leqslant n;\ i++ do 2 if {\rm random()} \leqslant{ \boldsymbol{p}}(h^{\rm e}|x'_{\rm e}x'_{\rm r}): x_{\rm e} = h^{\rm e} ; 3 else: x_{\rm e} = l^{\rm e} ; 4 x'_{\rm e} = x_{\rm e} ; 5 U_{i}^{\rm e} ={\boldsymbol{M}}^{\rm e}(x_{\rm e},\; x_{\rm r}) ; 6 return (\sum_{i=1}^{n} U_{i}^{\rm e})/n, \; x'_{\rm e} ; Algorithm 2. Evolved Strategy by ISP Input: {\boldsymbol{p}},\;{\boldsymbol{q}} , x_{\rm e} , previous state x'_{\rm e}, \;x'_{\rm r},\;{\boldsymbol{M}}^{t} , learning rate \theta , number of iterations n Output: U^{\rm e},\;{\boldsymbol{q}}, \;x'_{\rm r} 1 for i=1;\ i \leqslant n;\ i++ do 2 if {\rm random()} \leqslant{\boldsymbol{q}}(h^{\rm r}|x'_{\rm e}x'_{\rm r}): x_{\rm r} = h^{\rm r} ; 3 else: x_{\rm r} = l^{\rm r} ; 4 x'_{\rm r} = x_{\rm r} ; 5 U^{\rm r} = D(\mathit{\boldsymbol{p}},{\boldsymbol{q}},{\boldsymbol{M}}^{\rm r})/D(\mathit{\boldsymbol{p}},{\boldsymbol{q}},{\boldsymbol{1}}) ,; 6 U_{i}^{\rm r} ={\boldsymbol{M}}^{\rm r}(x_{\rm e},\; x_{\rm r}) ; 7 for \text{each element} q_{i}\in{\boldsymbol{q}} do 8 q_{i} = q_{i} + \theta \dfrac{\partial U^{\rm r}(\mathit{\boldsymbol{q}})}{\partial q_{i}} 9 return (\sum_{i=1}^{n} U_{i}^{\rm r})/n , {\boldsymbol{q}},\; x'_{\rm r} ; Fig.6 shows the comparison results of the ZD-VCS strategy and two classical strategies, i.e., TFT[46] and Pavlov[48]. The experiment starts from a random state of the game. It is obvious that the platform adopts the ZD-VCS strategy and the ISP takes either TFT or Pavlov, and the social welfare is approximately the same and is stable. However, when the platform changes its strategy to any other strategies, the social welfare is not dominated by the platform and is affected by the strategies of both players.
Fig.7 and Fig.8 show the utilities of the platform and the ISP respectively. The results are shown in Fig.7 when the platform adopts the ZD-VCS strategy, and the ISP takes the Evolved, ALLC, ALLD, and Random strategies. Fig.7(a) and Fig.7(b) show the average utilities for the platform and the ISP in all current iterations, respectively. From the results, we can see that the utilities of the platform and the ISP are becoming stable as the number of iterations increases. The corresponding total utilities (i.e., social welfare) are shown in Fig.5(a). Similarly, Fig.8 shows the results when the platform adopts the ZD-VCS strategy and the ISP takes the TFT, and Pavlov strategies. Fig.8(a) and Fig.8(b) show the mean utilities for the platform and the ISP in all current iterations, respectively. From the results, we can find that the utilities of the platform and the ISP gradually become stable as the number of iterations increases. Their corresponding total utilities are shown in Fig.6(a). From Fig.7 and Fig.8, we can find the utilities of the platform in a stable state are larger than those of the ISP in all the strategy pairs.
6.3.2 Experiments in the Continuous Model
In the continuous model, we adopt continuous strategies for the platform and the ISP. We assume that both the number of sensing tasks and the number of available RSUs are selected from [2, 8]. We first compare the social welfare when the platform adopts the ZD-VCS strategy and the normal strategies, such as the ALLC strategy p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = 1 , the ALLD strategy p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = 0 , and the Random strategy p(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm e}) = 1/(h^{\rm e} - l^{\rm e}) . As shown in Fig.9(a), when the platform adopts the ZD-VCS strategy, the social welfare becomes stable regardless of the ISP’s strategy (the ALLC strategy q(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm r}) = 1 , the ALLD strategy q(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm r}) = 0 , or the Random strategy q(x'_{\rm e},\; x'_{\rm r}, \; h^{\rm r}) = 1/(h^{\rm r} - l^{\rm r}) ). However, in Fig.9(b), Fig.9(c), and Fig.9(d), when the platform adopts the ALLC, ALLD, and Random strategies, it cannot control the social welfare.
Fig.10(a) shows that social welfare stays stable when the platform adopts the ZD-VCS strategy and the ISP adopts the TFT and Pavlov strategies. When the platform adopts the TFT and Pavlov strategies, it cannot control the social welfare as shown in Fig.10(b) and Fig.10(c). As shown in Fig.9(a) and Fig.10(a), the stable social welfare is slightly higher than that in the discrete model. Fig.11(a) and Fig.11(b) show the utilities of the platform. When it adopts the ZD-VCS strategy and the ISP adopts the ALLC, ALLD, and Random strategy, respectively, and the utility of the platform is higher than that of the ISP on the whole. Fig.12(a) and Fig.12(b) show the utilities of the platform adopting the ZD-VCS strategy and the ISP adopting the TFT and Pavlov strategies, respectively. Similarly, the utility of the platform is higher than that of the ISP.
6.4 Performance of the Extortion Strategy
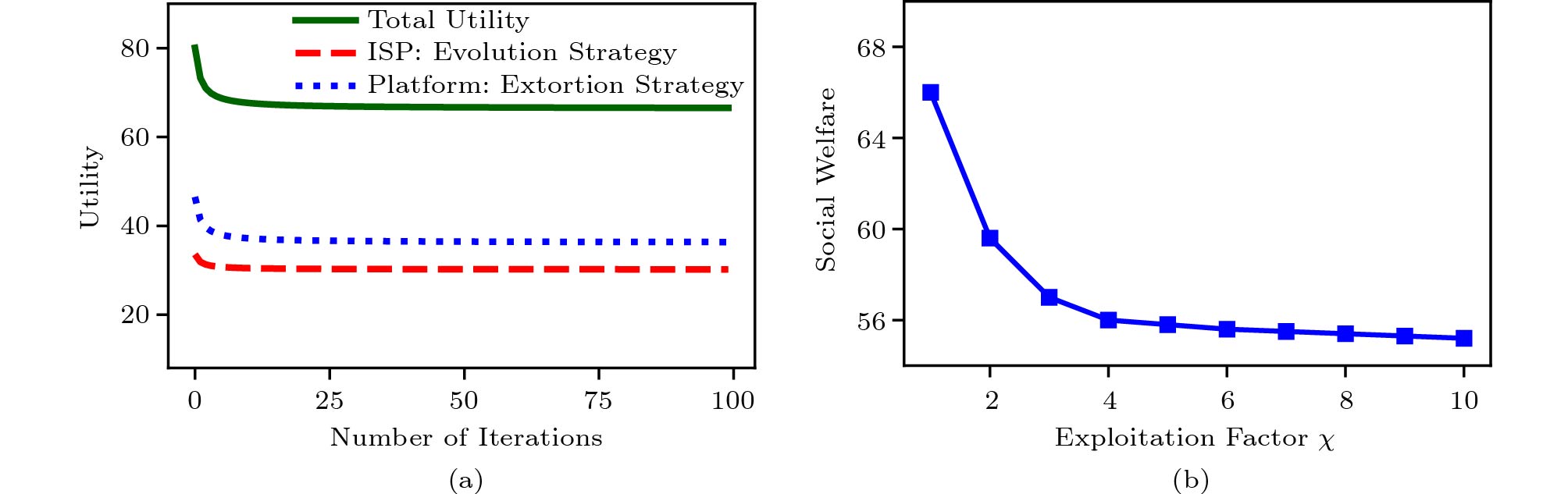
To evaluate the influence of social welfare when the platform adopts an extortion strategy, we do experiments in the iterated game with the platform adopting an extortion strategy and the ISP adopting an evolution strategy. Specifically, we set the extortion factor \chi = 2 , and the results are shown in Fig.13(a). The red dot line refers to the utility of the ISP adopting an evolution strategy, and the blue line refers to the utility of the platform adopting an extortion strategy. The platform’s utility is approximately twice as much as the ISP’s utility when both are minus a constant value. The solid green line represents the total utility (i.e., social welfare) of the platform and ISP, which is becoming stable as the number of iteration increases. However, the stable value is less than the value when the platform adopts the ZD-VCS strategy. Furthermore, we discuss the influence of different extortion factors on social welfare. Fig.13(b) shows that the social welfare first decreases sharply and then slowly as the extortion factor increases. When the extortion factor \chi = 1 , we set \alpha = \beta = 1 , which means the platform has no extortion to the ISP. Therefore the extortion strategy turns to the ZD-VCS strategy used in Subsection 5.2, and the social welfare is the same as that in Fig.5(a) and Fig.6(a).
6.5 Discussion
In some scenarios, as the traffic varies each day, the payoff matrices vary each day accordingly. Therefore, how to use the ZD-VCS strategy in practice is an issue. Usually, the traffic in a city or an area obeys a regular distribution during a period, and therefore we can predict the traffic each day according to the traffic histories (such as fitting a periodic function for prediction). Then, the predicted payoff matrix of each day could be calculated. Therefore, we can pre-calculate the ZD-VCS strategy adopted by the platform each day when the action space is discrete. Thus, the platform controls the social welfare at a high and stable value in the long term, which is shown in Fig.5(a) and Fig.6(a). Furthermore, when the utilities of the platform and the ISP are represented by continuous functions, the parameters of tasks and RSUs are continuous (parameters only make sense if they are integers), and then the ZD-VCS strategy is represented by a piece-wise function. The platform also controls the social welfare at a high and stable value, which is shown in Fig.9(a) and Fig.10(a).
In short, the utility function is appropriately represented by the utility matrix or the utility function. When an action space is discrete or continuous, the ZD-VCS strategy can be pre-calculated directly or represented by a piece-wise function. Then, the platform can adopt the ZD-VCS strategy and control the social welfare without considering the ISP’s strategy.
7. Conclusions
In this paper, we formulated the interaction between the platform and the ISP in vehicular crowdsensing as an iterated game, and addressed the problem of social welfare control in this game. We proposed a zero-determinant strategy for the vehicular crowdsensing platform strategy to control the social welfare without considering the ISP’s strategy. We theoretically analyzed that the platform can achieve stable and maximum possible social welfare regardless of the ISP’s strategy. Additionally, we investigated the influence of the extortion strategy on social welfare. Experimental results verified that the platform using the ZD-VCS strategy unilaterally controls the social welfare. In the future, we will study the different variants of the zero-determinant strategy and apply them in other scenarios.
-
Table 1 Description of Frequently-Used Notations
Notation Description E = \{ e_{\rm1},\; \ldots, \;e_{\rm M} \} Set of M candidate sensing tasks R = \{ r_{\rm1},\; \ldots, \; r_{\rm N} \} Set of N candidate RSUs x_{\rm e}/x_{\rm r} Number of selected sensing tasks/RSUs {\boldsymbol{W}} Task-RSU weighted traffic matrix \vec{{\boldsymbol{X}}_{\rm e}}/\vec{{\boldsymbol{X}}_{\rm r}} Vector of selected sensing tasks/RSUs f_{\rm g}/f_{\rm t} Payoff function of platform/ISP u_{\rm r}/u_{\rm t},\; C Energy cost/traffic cost, operating cost {\boldsymbol{M}}^{\rm e},\; {\boldsymbol{M}}^{\rm r} Payoff matrix of platform and ISP m^{\rm e}_{i},\; m^{\rm r}_{i} Elements in M^{\rm e} and M^{\rm r} {\boldsymbol{p}},\; {\boldsymbol{q}} Mixed strategy of platform and ISP {\boldsymbol{v}}_{\rm s}/ {\boldsymbol{f}} Stationary vector/any vector U^{\rm e}/ U^{\rm r}/ U_{\rm all} Utility of platform/ISP/both {\boldsymbol{H}} Markov state transition matrix \alpha,\;\beta,\;\gamma Parameters to determine the ZD-VCS strategy \chi Extortion factor l^{\rm r}/ l^{\rm e} Lowest number of RSU/sensing tasks h^{\rm r}/ h^{\rm e} Highest of RSU/sensing tasks -
[1] Song C, Wu J. Vehicular ad hoc/sensor networks in smart cities. In Mission-Oriented Sensor Networks and Systems: Art and Science: Volume 2: Advances, Ammari H M (ed.), Springer, 2019, pp.287–310. DOI: 10.1007/978-3-319-92384-0_9.
[2] Eriksson J, Girod L, Hull B, Newton R, Madden S, Balakrishnan H. The pothole patrol: Using a mobile sensor network for road surface monitoring. In Proc. the 6th International Conference on Mobile Systems, Applications, and Services, Jun. 2008, pp.29–39. DOI: 10.1145/1378600.1378605.
[3] Ganti R K, Ye F, Lei H. Mobile crowdsensing: Current state and future challenges. IEEE Communications Magazine, 2011, 49(11): 32–39. DOI: 10.1109/MCOM.2011.6069707.
[4] Guo B, Chen H, Yu Z, Xie X, Huangfu S, Zhang D. FlierMeet: A mobile crowdsensing system for cross-space public information reposting, tagging, and sharing. IEEE Trans. Mobile Computing, 2015, 14(10): 2020–2033. DOI: 10.1109/TMC.2014.2385097.
[5] Campioni F, Choudhury S, Salomaa K, Akl S G. Improved recruitment algorithms for vehicular crowdsensing networks. IEEE Trans. Vehicular Technology, 2019, 68(2): 1198–1207. DOI: 10.1109/TVT.2018.2885403.
[6] Ding R, Yang Z, Wei Y, Jin H, Wang X. Multi-agent reinforcement learning for urban crowd sensing with for-hire vehicles. In Proc. the 2021 IEEE Conference on Computer Communications, May 2021. DOI: 10.1109/INFOCOM42981.2021.9488713.
[7] Nash J F Jr. Equilibrium points in n-person games. Proceedings of the National Academy of Sciences of the United States of America, 1950, 36(1): 48–49. DOI: 10.1073/pnas.36.1.48.
[8] Wang E, Yang Y, Wu J, Wang H. Multi-round bidding strategy based on game theory for crowdsensing task. In Proc. the 12th International Conference on Security, Privacy, and Anonymity in Computation, Communication, and Storage, Jul. 2019, pp.196–210. DOI: 10.1007/978-3-030-24907-6_16.
[9] Liang C, He Y, Yu F R, Zhao N. Energy-efficient resource allocation in software-defined mobile networks with mobile edge computing and caching. In Proc. the 2017 IEEE Conference on Computer Communications Workshops, May 2017, pp.121–126. DOI: 10.1109/INFCOMW.2017.8116363.
[10] Okic A, Zanzi L, Sciancalepore V, Redondi A, Costa-Pérez X. π-ROAD: A learn-as-you-go framework for on-demand emergency slices in V2X scenarios. In Proc. the 2021 IEEE Conference on Computer Communications, May 2021. DOI: 10.1109/INFOCOM42981.2021.9488677.
[11] Ozkaptan C D, Ekici E, Altintas O. Enabling communication via automotive radars: An adaptive joint waveform design approach. In Proc. the 2020 IEEE Conference on Computer Communications, Jul. 2020, pp.1409–1418. DOI: 10.1109/INFOCOM41043.2020.9155527.
[12] Hu Q, Wang S, Bie R, Cheng X. Social welfare control in mobile crowdsensing using zero-determinant strategy. Sensors, 2017, 17(5): Article No. 1012. DOI: 10.3390/s17051012.
[13] Hu Q, Wang S, Ma L, Bie R, Cheng X. Anti-malicious crowdsourcing using the zero-determinant strategy. In Proc. the 37th IEEE International Conference on Distributed Computing Systems, Jun. 2017, pp.1137–1146. DOI: 10.1109/ICDCS.2017.46.
[14] Tang C, Li X, Cao M, Zhang Z, Yu X. Incentive mechanism for macrotasking crowdsourcing: A zero-determinant strategy approach. IEEE Internet of Things Journal, 2019, 6(5): 8589–8601. DOI: 10.1109/JIOT.2019.2921348.
[15] Hu Q, Wang S, Ma P, Cheng X, Lv W, Bie R. Quality control in crowdsourcing using sequential zero-determinant strategies. IEEE Trans. Knowledge and Data Engineering, 2020, 32(5): 998–1009. DOI: 10.1109/TKDE.2019.2896926.
[16] Hu Q, Wang S, Cheng X. A game theoretic analysis on block withholding attacks using the zero-determinant strategy. In Proc. the 2019 International Symposium on Quality of Service, Jun. 2019, Article No.41. DOI: 10.1145/3326285.3329076.
[17] Zhang H, Niyato D, Song L, Jiang T, Han Z. Equilibrium analysis for zero-determinant strategy in resource management of wireless network. In Proc. the 2015 IEEE Wireless Communications and Networking Conference, Mar. 2015, pp.2002–2007. DOI: 10.1109/WCNC.2015.7127775.
[18] Chakeri A, Wang X, Goss Q, Akbas M I, Jaimes L G. A platform-based incentive mechanism for autonomous vehicle crowdsensing. IEEE Open Journal of Intelligent Transportation Systems, 2021, 2: 13–23. DOI: 10.1109/OJITS.2021.3056925.
[19] Di Stefano A, Scatá M, Attanasio B, La Corte A, Lió P, Das S K. A novel methodology for designing policies in mobile crowdsensing systems. Pervasive and Mobile Computing, 2020, 67: 101230. DOI: 10.1016/j.pmcj.2020.101230.
[20] Xiao L, Chen T, Xie C, Dai H, Poor H V. Mobile crowdsensing games in vehicular networks. IEEE Trans. Vehicular Technology, 2018, 67(2): 1535–1545. DOI: 10.1109/TVT.2016.2647624.
[21] Dai Z, Wang H, Liu C H, Han R, Tang J, Wang G. Mobile crowdsensing for data freshness: A deep reinforcement learning approach. In Proc. the 2021 IEEE Conference on Computer Communications, May 2021. DOI: 10.1109/INFOCOM42981.2021.9488791.
[22] Keremoğlu E, Weidmann N B. How dictators control the internet: A review essay. Comparative Political Studies, 2020, 53(10/11): 1690–1703. DOI: 10.1177/0010414020912278.
[23] Press W H, Dyson F J. Iterated prisoner’s dilemma contains strategies that dominate any evolutionary opponent. Proceedings of the National Academy of Sciences of the United States of America, 2012, 109(26): 10409–10413. DOI: 10.1073/pnas.1206569109.
[24] Pu L, Chen X, Mao G, Xie Q, Xu J. Chimera: An energy-efficient and deadline-aware hybrid edge computing framework for vehicular crowdsensing applications. IEEE Internet of Things Journal, 2019, 6(1): 84–99. DOI: 10.1109/JIOT.2018.2872436.
[25] Morselli F, Zabini F, Conti A. Environmental monitoring via vehicular crowdsensing. In Proc. the 29th IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Sept. 2018, pp.1382–1387. DOI: 10.1109/PIMRC.2018.8580783.
[26] Stewart A J, Plotkin J B. From extortion to generosity, evolution in the iterated prisoner’s dilemma. Proceedings of the National Academy of Sciences of the United States of America, 2013, 110(38): 15348–15353. DOI: 10.1073/pnas.1306246110.
[27] Roemheld L. Evolutionary extortion and mischief zero determinant strategies in iterated 2x2 games. arXiv: 1308.2576, 2013. https://arxiv.org/abs/1308.2576, Mar. 2025.
[28] Hu Q, Wang S, Cheng X, Ma L, Bie R. Solving the crowdsourcing dilemma using the zero-determinant strategies. IEEE Trans. Information Forensics and Security, 2020, 15: 1778–1789. DOI: 10.1109/TIFS.2019.2949440.
[29] Zhang H, Niyato D, Song L, Jiang T, Han Z. Zero-determinant strategy for resource sharing in wireless cooperations. IEEE Trans. Wireless Communications, 2016, 15(3): 2179–2192. DOI: 10.1109/TWC.2015.2499185.
[30] He X, Dai H, Ning P, Dutta R. Zero-determinant strategies for multi-player multi-action iterated games. IEEE Signal Processing Letters, 2016, 23(3): 311–315. DOI: 10.1109/LSP.2016.2517640.
[31] McAvoy A, Hauert C. Autocratic strategies for iterated games with arbitrary action spaces. Proceedings of the National Academy of Sciences of the United States of America, 2016, 113(13): 3573–3578. DOI: 10.1073/pnas.1520163113.
[32] Tan R, Su Q, Wu B, Wang L. Payoff control in repeated games. In Proc. the 33rd Chinese Control and Decision Conference, May 2021, pp.997–1005. DOI: 10.1109/CCDC52312.2021.9602002.
[33] Li L, Yu X, Cai X, He X, Liu Y. Contract-theory-based incentive mechanism for federated learning in health crowdsensing. IEEE Internet of Things Journal, 2023, 10(5): 4475–4489. DOI: 10.1109/JIOT.2022.3218008.
[34] Jiang C, Gao L, Duan L, Huang J. Exploiting data reuse in mobile crowdsensing. In Proc. the 2016 IEEE Global Communications Conference, Dec. 2016. DOI: 10.1109/GLOCOM.2016.7841828.
[35] Liu W, Yang Y, Wang E, Wu J. Dynamic user recruitment with truthful pricing for mobile crowdsensing. In Proc. the 2020 IEEE Conference on Computer Communications, Jul. 2020, pp.1113–1122. DOI: 10.1109/INFOCOM41043.2020.9155242.
[36] Xiao M, Gao G, Wu J, Zhang S, Huang L. Privacy-preserving user recruitment protocol for mobile crowdsensing. IEEE/ACM Trans. Networking, 2020, 28(2): 519–532. DOI: 10.1109/TNET.2019.2962362.
[37] Lyamin N, Vinel A, Jonsson M, Loo J. Real-time detection of denial-of-service attacks in IEEE 802.11p vehicular networks. IEEE Communications Letters, 2014, 18(1): 110–113. DOI: 10.1109/LCOMM.2013.102213.132056.
[38] Wu T J, Liao W, Chang C J. A cost-effective strategy for road-side unit placement in vehicular networks. IEEE Trans. Communications, 2012, 60(8): 2295–2303. DOI: 10.1109/TCOMM.2012.062512.100550.
[39] Mehmeti F, Spyropoulos T. Is it worth to be patient? Analysis and optimization of delayed mobile data offloading. In Proc. the 2014 IEEE Conference on Computer Communications, May 2014. DOI: 10.1109/INFOCOM.2014.6848181.
[40] Zhou C, Tham C K, Motani M. Online auction for scheduling concurrent delay tolerant tasks in crowdsourcing systems. Computer Networks, 2020, 169: 107045. DOI: 10.1016/j.comnet.2019.107045.
[41] Mantri D, Prasad N R, Prasad R. Grouping of clusters for efficient data aggregation (GCEDA) in wireless sensor network. In Proc. the 3rd IEEE International Advance Computing Conference, Feb. 2013, pp.132–137. DOI: 10.1109/IAdCC.2013.6514208.
[42] Xu J, Yang S, Lu W, Xu L, Yang D. Incentivizing for truth discovery in edge-assisted large-scale mobile crowdsensing. Sensors, 2020, 20(3): 805. DOI: 10.3390/s20030805.
[43] Zheng Z, Peng Y, Wu F, Tang S, Chen G. Trading data in the crowd: Profit-driven data acquisition for mobile crowdsensing. IEEE Journal on Selected Areas in Communications, 2017, 35(2): 486–501. DOI: 10.1109/JSAC.2017.2659258.
[44] Sheng B, Li Q, Mao W. Data storage placement in sensor networks. In Proc. the 7th ACM International Symposium on Mobile ad Hoc Networking and Computing, May 2006, pp.344–355. DOI: 10.1145/1132905.1132943.
[45] Burkhardt T, Leopold A, Leopold-Wildburger U. Markov simulation of an iterated prisoners’ dilemma experiment. In Proc. the 2011 Selected Papers of the International Conference on Operations Research on Operations Research Proceedings, Sept. 2012, pp.223–228. DOI: 10.1007/978-3-642-29210-1_36.
[46] Lacey N. The Prisoners’ Dilemma. Cambridge University Press, 2008: pp.9–17. DOI: 10.1017/CBO9780511819247.
[47] Akbay A B, Zhang J. Distributed learning with strategic users: A repeated game approach. In Proc. the 36th AAAI Conference on Artificial Intelligence, Jun. 2022, pp.5976–5983. DOI: 10.1609/aaai.v36i6.20543.
[48] Imhof L A, Fudenberg D, Nowak M A. Tit-for-tat or win-stay, lose-shift? Journal of Theoretical Biology, 2007, 247(3): 574–580. DOI: 10.1016/j.jtbi.2007.03.027.
-
其他相关附件




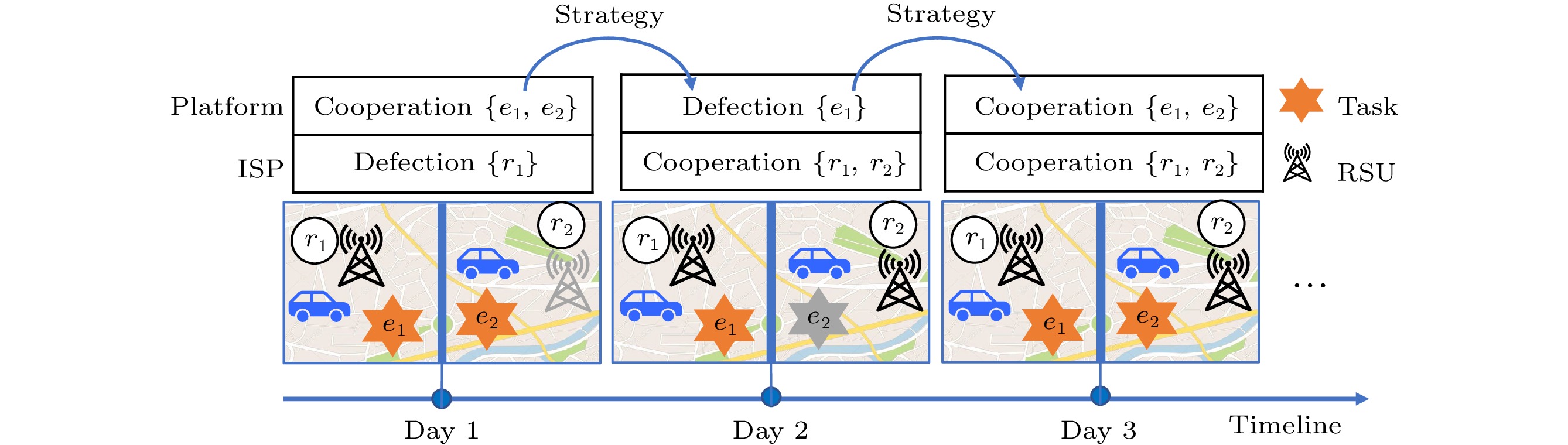
 下载:
下载: