支付通道网络个性化隐私保护路由机制
Personalized Privacy-Preserving Routing Mechanism Design in Payment Channel Network
-
摘要:研究背景
支付通道网络加快了区块链网络的交易确认速度。为进一步提升支付通道交易效率,研究人员提出了针对不同优化目标的路由机制,最小化成本是其中的主流研究方向。然而,当前的路由机制中,忽略了用户的策略行为以及用户的隐私需求,使得提出的路由机制易受到激励攻击以及隐私攻击的威胁。因此,本文针对支付通道交易中存在的用户策略行为和隐私泄漏问题展开研究,旨在设计能抵御用户策略行为并为用户提供个性化差分隐私保护的最小成本交易路由机制。
目的对于交易发起者而言,交易路由的成本是其最关心的,所以本文设计的路由机制的优化目标是最小化交易路由的成本。用户参与是支付通道运行的重要基础,而公平性和安全性对用户是否愿意参与路由具有重要影响。如果用户从策略行为中获利,将会影响网络中竞争的公平性。因此,需要设计一个具有真实性的激励机制抵御用户的策略行为。同时,在参与路由的过程中,用户有隐私性需求,并且每个用户的隐私需求是不一致的,那么为用户提供个性化差分隐私保护能够吸引用户参与路由。
方法个性化差分隐私路由机制是基于拍卖机制和差分隐私机制的。首先,每个用户根据自己的隐私需求,通过拉普拉斯机制在交易成本上添加噪声,并上报添加噪声后的交易成本。其次,当交易发起者收集到用户上报的添加噪声的交易成本后,基于设计的带约束的K最短路径算法,得到前K条最短路径。第三,在K条最短路径中,分别比较两条路径之间的真实路径成本小的概率,并选择具有最小真实成本的概率最大的路径作为最终路由。最后,利用梅尔森定理和二分搜索,计算路由中每个用户的交易费用。
结果通过理论分析证明,本文提出的个性化差分隐私路由机制能够分别以1/2和1/4的概率保证用户的真实性和个体理性。实验数据采用了Ripple的真实网络和交易数据。相比于无隐私保护的路由机制,本文提出的具有个性化差分隐私保护的路由机制,在牺牲了13.2%的路径成本的情况下,为用户提供个性化差分隐私保护。
结论本文提出的具有个性化差分隐私保护的路由机制,能够以牺牲较小的成本为代价,为每个用户提供个性化的差分隐私保护。该机制不仅保证了支付通道网络的路由成本,同时提升了支付通道的安全性能,满足了用户的个性化隐私需求。个性化隐私服务框架可以提升支付通道网络中用户的满意度和参与度,使得用户更愿意参与路由,从而使得路由的选择更加灵活,网络整体性能更好。该框架未来可以进一步应用于支付通道网路中的通道容量、交易时间等隐私信息的保护。
Abstract:Payment Channel Network (PCN) provides the off-chain settlement of transactions. It is one of the most promising solutions to solve the scalability issue of the blockchain. Many routing techniques in PCN have been proposed. However, both incentive attack and privacy protection have not been considered in existing studies. In this paper, we present an auction-based system model for PCN routing using the Laplace differential privacy mechanism. We formulate the cost optimization problem to minimize the path cost under the constraints of the Hashed Time-Lock Contract (HTLC) tolerance and the channel capacity. We propose an approximation algorithm to find the top K shortest paths constrained by the HTLC tolerance and the channel capacity, i.e., top K-restricted shortest paths. Besides, we design the probability comparison function to find the path with the largest probability of having the lowest path cost among the top K-restricted shortest paths as the final path. Moreover, we apply the binary search to calculate the transaction fee of each user. Through both theoretical analysis and extensive simulations, we demonstrate that the proposed routing mechanism can guarantee the truthfulness and individual rationality with the probabilities of 1/2 and 1/4, respectively. It can also ensure the differential privacy of the users. The experiments on the real-world datasets demonstrate that the privacy leakage of the proposed mechanism is 73.21% lower than that of the unified privacy protection mechanism with only 13.2% more path cost compared with the algorithm without privacy protection on average.
-
1. Introduction
Blockchain provides a promising solution for distributed ledgers, and has been widely used in the cryptocurrencies, such as Bitcoin[1], Ripple
1 , and Ethereum[2]. The number of transactions in blockchain had reached to250000 per day in July 2021. However, Bitcoin and Ethereum can only process at most 15 transactions per second2 , which is much less than65000 transactions per second of Visa3 . Since each transaction in blockchain needs to be confirmed by the entire network, the blockchain-based transactions consume a large amount of resources (e.g., storage, communication, and computing resources)[3]. The scalability problem of the blockchain largely impedes its development. A novel and efficient approach to solving the scalability issue of the blockchain is the payment channel[4].The payment channel is designed to solve the scalability problem of the blockchain. The advantage of the payment channel is that there is no need to commit every transaction to the blockchain. Each user only needs to upload the channel state and the deposit to the blockchain when the channel is established or closed, and the details of transactions do not need to be uploaded to the blockchain. The lifetime of a payment channel consists of three phases[4]: channel establishment, transition, and dispute. The users first establish a peer-to-peer (P2P) channel with deposits, and transfer funds by adjusting the deposit allocation in the channel. When any user wants to disconnect from the channel or any user's deposit in the channel becomes zero, the users on both sides of the channel will enter the dispute phase. The final deposits of this channel are published in the blockchain. After the confirmation of the final deposits by the blockchain, the payment channel is closed.
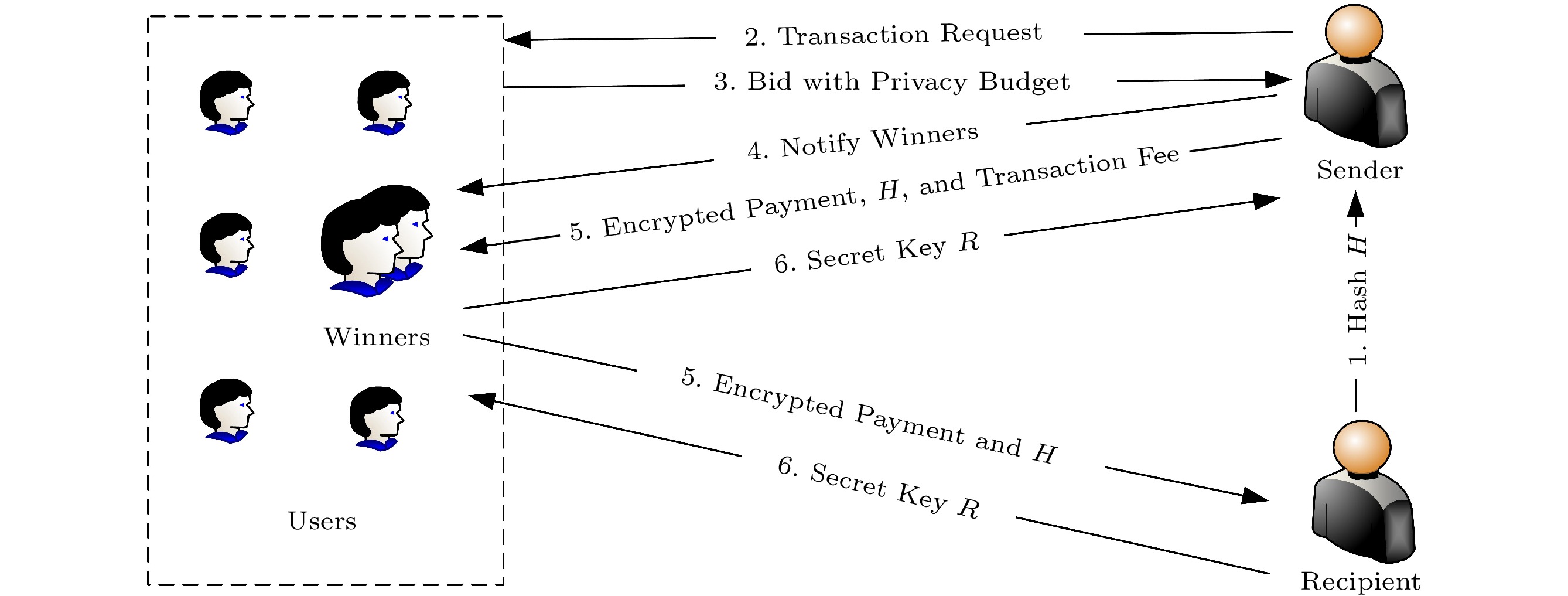
Multiple payment channels together form a payment channel network (PCN), and the transactions in PCN follow the Hashed Time-Lock Contract (HTLC)[4]. The users in PCN have payment channels with their neighbors. An example of PCN with five users (w0,w1,w2,w3,w4) is illustrated in Fig.1. Consider that user w0 wants to transfer payment to user w4. The recipient w4 first generates a random value R, then sends its hash H to the sender w0 by communication links. Once the route (e.g., w0→w3→w2→w4) from w0 to w4 has been found, the payment, transaction fee, and H are transferred and temporarily stored in the intermediate users (i.e., w3,w2) along the route. After receiving the payment, the recipient w4 sends the secret R via the reverse route, and each intermediate user of the route obtains its own transaction fee only when it receives the secret R from its predecessor in the reverse route. In addition, the transaction is restricted by the HTLC tolerance. Each user has an HTLC tolerance for its every payment channel, which is the upper bound on time for transaction. If any user in the route cannot receive secret R within its HTLC tolerance, the transaction is failed, and the payment and transaction fee will be sent back to the sender along the reverse route. When the sender receives secret R, the transaction is completed finally.
The route calculated by the sender is based on the information (i.e., channel capacity, HTLC tolerance, transaction fee, etc.) submitted by the users. In the payment channel network, the information transfer is with the help of the routing table stored in each user. The transaction fee for each selected user is based on their bidding transaction cost. These methods will generate the incentive attack and the differential privacy attack. Therefore, it is essential to design a routing mechanism for resisting the incentive attack and the differential privacy attack.
The routing decision in PCN is based on the users’ information. From the sender's perspective, it aims to minimize the total transaction fee of the selected route[5–7]. Most studies on PCN routing assume that the users are honest. However, the users are often selfish and rational, and may take a strategic behavior by claiming dishonest transaction cost (i.e., the bidding transaction cost is inequal to the transaction cost) to improve their own utilities. The incentive attack will undermine fairness and make users reluctant to participate in transaction. The strategy-proof routing mechanism can eliminate the fear of market manipulation and the overhead of strategizing over others for the users. Thus, it is essential to develop a truthful routing mechanism to reveal the users’ transaction costs. Note that the term “transaction cost” stands for the cost for payment transfer through the payment channel rather than the cost to create or close the payment channel in this paper. The transaction cost indicates that the user has a cost to transfer the payment through its payment channel. The consumption of the channel capacity of users may make the users cannot undertake subsequent transactions. Thus, the consumption of the channel capacity needs to be compensated. Auction is an efficient method to design truthful mechanisms and has been widely used in many fields, such as mobile crowdsensing[8–10], edge computing[11, 12], spectrum allocation[13], and blockchain systems[14]. In this paper, we model the routing decision of PCN transactions as a reverse auction. Note that the transaction fee may be different from the transaction cost in the auction.
In a truthful auction-based routing mechanism[15], the users are stimulated to submit their transaction costs, which are the private information of the users. For transparency, the outcome of the auction mechanism will be published, which consists of the winners and their transaction fees. The malicious users could infer others’ transaction costs according to the outcome of the mechanism (elaborated in Section 3). Then, the transaction costs of the attacked users may be inferred and the attacked users may lose in next auction, which make users reluctant to participate in PCN. Therefore, it is essential to design a privacy protection mechanism to protect the transaction costs of the users. The encrypted methods are often used to protect the privacy of the users. However, differential privacy attack is that the attacker guesses the privacy of the attacked users by constantly changing its own bids. Hence, the encrypted methods cannot resist the differential privacy attack. Differential privacy[16] provides formal privacy guarantees for users in data analysis. The mechanism is differentially private[17] if the outcome cannot be used to infer any user's private information, when the change of user's bid is small enough. Compared with other privacy protection methods (anonymity[18], encryption[19], etc.), differential privacy does not need to make any assumptions about the attacker's ability and auxiliary information. However, the original differential privacy only provides the uniform level of privacy protection for all users or data. Actually, the importance of data and the privacy requirements of the users are not uniform. In this paper, we consider that the users can require different levels of privacy protection for their transaction costs personally. Different privacy protection levels correspond to different privacy budgets. Smaller privacy budget corresponds to lower privacy leakage, which leads to a lower privacy cost. However, small privacy budget results in poor precision of the bidding cost, which may decrease the utility of the user. Thus, the privacy budget is the trade-off between the privacy protection level and the utility. From the perspective of PCN, small privacy budget results in high path cost since more noise is added. In this paper, we employ the Laplace differential privacy mechanism[20] to protect users’ transaction costs.
In this paper, we aim to design the truthful privacy-preserving routing mechanism for the off-chain transactions in PCN through the reverse auction and the differential privacy technique. We model the routing decision process as the reverse auction, where the buyer is the sender of the transaction, and the sellers are the potential intermediate users (termed users for short). Meanwhile, the differential privacy mechanism is used to protect the transaction costs of the users. The objective of our routing mechanism is to minimize the path cost (sum of the transaction cost and the privacy cost of all the winners in the path) such that: 1) the channel capacity of each payment channel in the path is feasible for the transaction; 2) the HTLC tolerance of each user in the path is satisfied.
Designing an auction-based personalized differential privacy routing mechanism in PCN is very challenging. First, due to the Laplace noise, the path with the lowest obfuscated bidding path cost may not be the exact path with the lowest cost. Thus, the method for finding the path which has the largest probability of having the lowest cost is needed. Second, to find the path with the largest probability, we have to compare the probabilities between any pair of feasible paths. However, it takes exponential time. Moreover, each user may take a strategic behavior by submitting dishonest transaction cost to maximize its utility. Since the final path is selected through the probability comparison, the final path selection may not be monotone. Hence, it is hard to find the critical value of the transaction fee of a winner (i.e., the highest transaction cost a winner can bid). The critical value calculation of the transaction fee of a user is the key to guarantee the properties of truthfulness and individual rationality, which poses a challenge to the design of the incentive mechanism.
The main contributions of this paper are as follows.
● To the best of our knowledge, this is the first work to design an auction-based and personalized differential privacy routing mechanism in PCN.
● We present the system model for PCN routing using the Laplace mechanism, and formulize the cost optimization routing (COR) problem to minimize the path cost under the constraints of the HTLC tolerance and the channel capacity.
● We propose the Personalized Privacy-Preserving Routing Mechanism (P3RM). We show that P3RM guarantees the truthfulness and individual rationality with the probabilities of 1/2 and 1/4, respectively. Moreover, it achieves ∑qi=0max(ϵi) differential privacy, where q is the length of the final path, and max(ϵi) is the maximum privacy budget of all payment channels for user wi in the final path.
● The extensive simulations based on the real-world datasets demonstrate that the privacy leakage of P3RM is 73.21% lower than that of the unified privacy protection mechanism with only 13.2% more path cost compared with the algorithm without privacy protection on average.
The rest of this paper is organized as follows. Section 2 reviews the state-of-the-art research. Section 3 presents the auction model and the threat models, and formulates the COR problem, and lists some desirable properties. Section 4 presents the detailed design of our routing mechanism, and the theoretical analysis of the routing mechanism. We evaluate the performance of our routing mechanism in Section 5, and conclude the paper in Section 6.
2. Related Work
Several PCN routing mechanisms have been proposed. Zhang et al.[5] regarded the transmission deadline constraint as the routing hop constraint, and proposed a distributed algorithm to find the optimal path for payment routing by the Bellman-Ford algorithm. Yu et al.[7] took into account the timeliness of the transactions, and proposed a routing model based on network flow and concurrent flow so that the payments in PCN could reach the recipient through multiple paths. The authors used the Ford-Fulkerson max-flow algorithm to find the max transaction flow from the sender to the recipient. Zhang et al.[21] proposed an extended routing algorithm based on the multi-hop Delaunay Triangulation to achieve low delay and low probing overhead. Khalil and Gervais[22] took into consideration the remaining deposits in the channels, and proposed a routing algorithm to solve the problem of the channel balance with the purpose of prolonging the lifetime of PCN. In [23], the authors proposed a robust payment routing protocol, which constructs two or more node-disjoint payment paths. Each payment path can fulfill the payment request. The main optimization objective of these routing algorithms mentioned above is to find the shortest transaction path in PCN. However, all these studies do not solve the problems of the privacy leakage of the transaction cost and the strategic behavior of the users.
Some efforts have been made to protect users’ privacy in PCN. Tripathy and Mohanty[24] proposed a multi-hop, anonymous privacy preserving PCN based on Elliptic Curve Cryptography, which can ensure the balance and the payment privacy, and prevent the stealing transfer fee attack. Mazumdar and Ruj[25] also designed an atomic multi-path payment protocol to guarantee the value privacy and resist the worm attack. Yu et al.[26] proposed the Chameleon Hash function based payment protocol to resist the malicious users to recover the payment paths. Thus, it can protect the balance security, value privacy, and the identities of users in the paths. In [27], the authors uncovered a balance discovery attack in PCN, and discussed some potential countermeasures to handle the attack. Tang et al.[28] proposed a noise mechanism to protect the balance, and revealed the trade-off between the utility and the privacy. SpeedyMurmurs generates anonymous addresses for the sender and the recipient to protect their identities[29]. Based on the anonymous addresses, SpeedyMurmurs uses embedding-based path discovery to find the route from the sender to the recipient. Li et al.[30] moved PCN-related modules into the trusted execution environment and sent the redundant transactions to the pseudo recipients, which can confuse adversaries and prevent the intermediate users from collusion to obtain the payment amounts and the payment recipient. The methods mentioned above take into consideration the value privacy, payment security, and the identities of the users; however, users’ strategic behaviors are neglected. The users may falsely report their own information to gain more benefits.
Differential privacy was first proposed in [16]. The commonly used differential privacy mechanisms include the Laplace mechanism, Gaussian mechanism, and Exponential mechanism. The first two mechanisms mainly aim at numerical output functions and can be applied to develop the personalized privacy protection mechanisms[20]. The exponential mechanism[31] is mainly used in non-numerical output functions. The personalized differential privacy[32] is derived from differential privacy to provide different privacy protection levels for users or database based on its privacy requirements. Different from the standard differential privacy, if the noise adding process is implemented by the users, it is called local differential privacy[33]. The differential privacy technique is widely used in various fields, such as spectrum system[34], mobile crowdsensing system[35], big data[36], edge computing[37], and machine learning[38]. However, there is no differential privacy mechanism to protect users’ privacy information in PCN routing. Note that our object is finding the transaction route in PCN. Therefore, the exponential mechanism cannot be used since it cannot guarantee that the winners selected based on the score function of the exponential mechanism can form a path definitely. On the other hand, if we use the exponential mechanism to select the path directly, all candidate paths should be found in advance, which takes exponential time. In this paper, we use the Laplace mechanism to protect the users’ transaction costs. The designed mechanism has no assumption about the attacker's ability, and can provide personalized differential privacy protection for each user.
3. Model and Problem Formulation
3.1 Auction Model
At the beginning of the auction, sender s publicizes a transaction request to all users in the PCN. Recipient d and payment g are the private information of sender s, which are not publicized. Assume that a set U of users are interested in transferring the payment. Each user wi∈U submits a bid Bi=(Bi1,Bi2,…,BiNi) to the sender, where Ni is the number of the bidding payment channels of the user wi. Bij is user wi's bid for the payment channel <i,j>, j∈{1,2,…,Ni}. Bij is a quintuple (¯btij,rij,tij,ϵij,σij), where ¯btij,rij,tij,ϵij, and σij are obfuscated bidding transaction cost, channel capacity, transaction time, privacy budget, and the HTLC tolerance of the payment channel <i,j>, respectively. The transaction cost of the payment channel <i,j> is ctij, which is the private information and known only to user wi. btij is the bidding transaction cost of user wi, and it may differ from ctij. The transaction time tij is the sum of time consumption for transferring payment to user wj and transmitting secret R to user wi, and can be estimated from historical data. The privacy budget ϵij∈(0,1] represents any user wi's desired privacy protection level of transaction cost on the payment channel <i,j>. The smaller the privacy budget is, the better privacy protection level there will be.
We consider that each user will honestly report the channel capacity, transaction time, and HTLC tolerance because the information can be easily verified by the transactions and PCN. Moreover, the privacy of the channel capacity, transaction time, and HTLC tolerance can be protected through the methods used in [24–26].
Given the transaction request T and the bid profile \boldsymbol{B} =(B_{1},\;B_{2},\;\ldots ,\;B_{n}) , the sender calculates the winning payment channel set to form a path l_{f} from the sender to the recipient, and the transaction fee p_{ij} for each winning payment channel < i,\; j >\;\in l_{f} . A user w_{i} is called a winner and is added into the winner set S_{f} if one of its payment channels is selected as the winning payment channel, i.e., (\bigcup \{ < i,\; j > \})\cap l_{f} \neq \varnothing , j\in \lbrace{1,\;2,\;\ldots ,\;N_{i}}\rbrace . Since l_{f} contains at most one payment channel of any winner w_{i} , the transaction fee of each winner w_{i} can be represented as p_{i}=p_{ij} , < i,\; j >\;\in l_{f} .
We denote the privacy cost of any user w_{i} for any payment channel < i,\; j > as c_{ij}^{p} . The privacy cost c_{ij}^{p} represents the privacy threat to user w_{i} when using the payment channel < i,\; j > to transfer the payment. The larger of the privacy budget is, the higher the privacy leakage is. We adopt the linear relationship between the user's privacy cost and its privacy budget, which is widely used in the studies on differential privacy[20].
c_{ij}^{p} =\alpha \epsilon_{ij}, where \alpha > 0 is the coefficient to scale the value of privacy cost.
For any < i,\; j >\;\in l_{f} , the cost of winner w_{i} is
c_{i} =c_{ij}^{t}+c_{ij}^{p}. We assume the maximum cost for establishing a payment channel is C_{\rm{max}} . We consider that C_{\rm{max}} is large enough so that c_{i} \leqslant C_{\rm{max}} and p_{i} \leqslant C_{\rm{max}} for \forall w_{i} \in U . Otherwise, the sender can establish a direct payment channel connecting the recipient with cost at most C_{\rm{max}} .
We define the utility of any user w_{i} as the difference between the transaction fee and its cost:
u_{i} = \begin{cases} p_{i}-c_{i}, & i\in S_{f}, \\ 0, & \rm{otherwise}. \\ \end{cases} (1) Then, a PCN G = (W,E) can be constructed. W is the set of users in the whole network, which contains the sender, the recipient, and the users who are interested in transferring the payment. E is the set of users’ bidding payment channels. Without loss of generality, we consider that there are n users and m channels in the PCN. Each channel < i,\; j >\;\in E is with an obfuscated bidding transaction cost \overline{b_{ij}^{t}} , channel capacity r_{ij} , transaction time t_{ij} , privacy budget \epsilon_{ij} , and HTLC tolerance \sigma_{ij} .
The whole process of the auction-based PCN transaction is illustrated in Fig.2. We consider that the auction-based PCN transactions follow the standard HTLC. 1) The recipient generates a random value R, and then sends its hash H to the sender. 2) The sender publicizes a transaction request to all users in PCN. 3) Each user submits its bid with the privacy budget. 4) The sender selects a subset of users to establish a path from the sender to the recipient, and notifies the winners of the determination. 5) The sender sends the encrypted payment, transaction fee, and H to the recipient along the path hop-by-hop. 6) After the recipient receives the payment, the recipient will send the key R to its successor along the reverse path. When a winner receives R from its predecessor, it obtains the transaction fee, which is determined by the sender to compensate the transaction cost and privacy cost of the winners. Then the winner further transfers R to its successor. When the sender receives R, the transaction is completed.
3.2 Threat Model
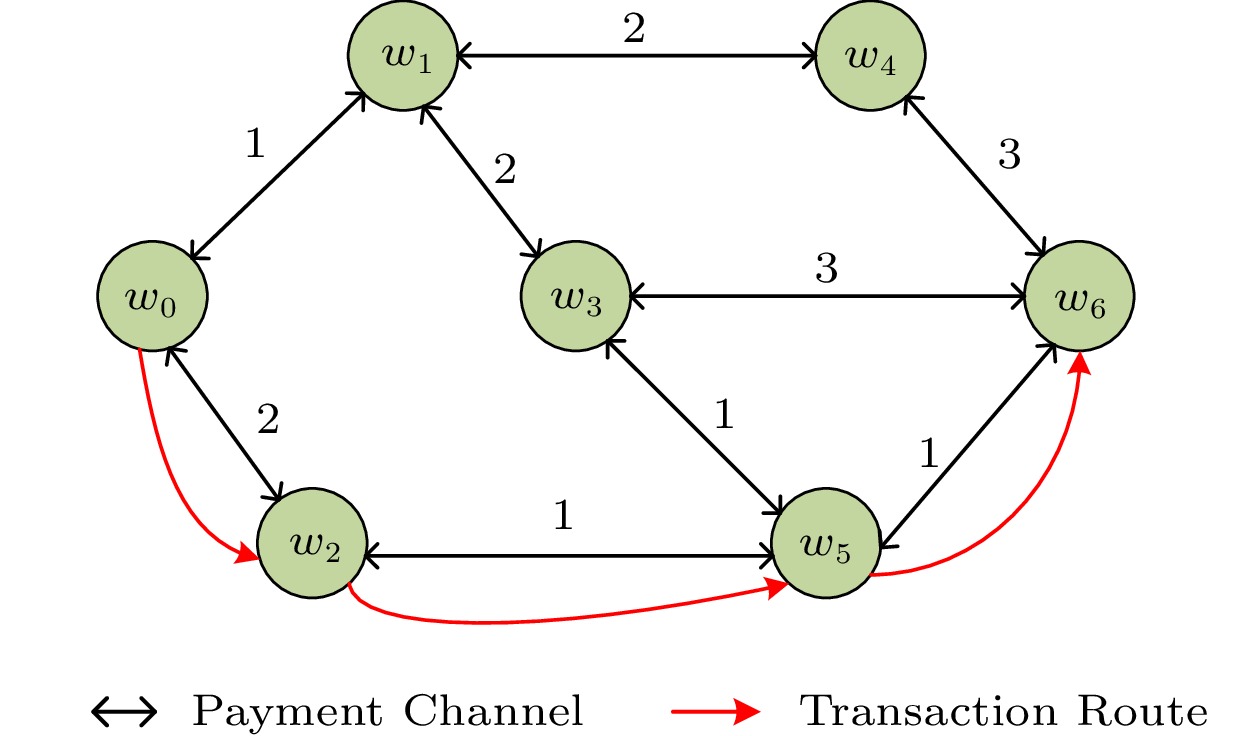
Threats to Incentive. As shown in Fig.3, the number on each channel is the transaction cost of each channel. We assume that the transaction cost of the two directions on one channel are the same. When user w_{0} transfers payment to user w_{6} , the path with the lowest transaction cost is w_{0}\rightarrow w_{2}\rightarrow w_{5}\rightarrow w_{6} , and the transaction fee of user w_{2} is 1. We suppose that user w_{2} bids 1.5 of channel < w_{2}, w_{5} > , which is different from the transaction cost 1. Although the path with the lowest transaction cost does not change, user w_{2} 's transaction fee increases to 1.5, thus, the utility of user w_{2} increases. Therefore, the users have an incentive to misreport the transaction costs to increase their utilities.
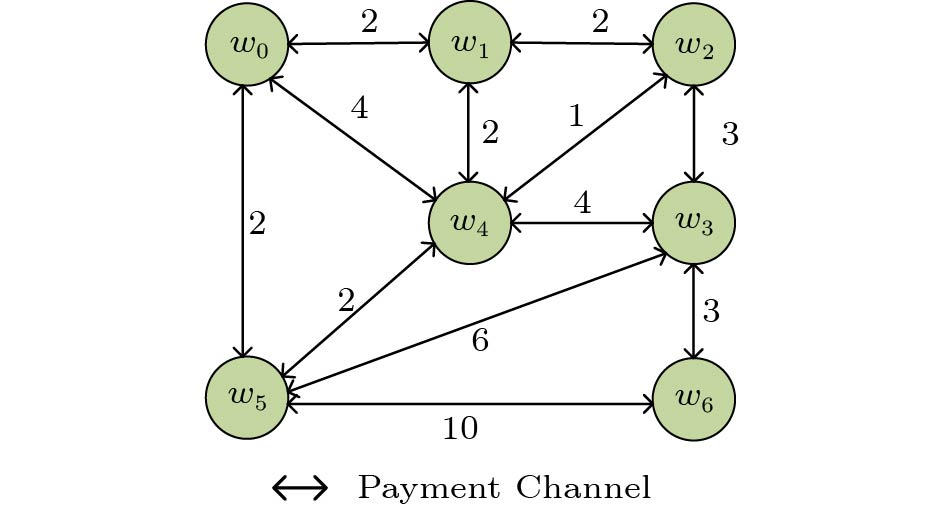
Threats to Privacy. As shown in Fig.4, we assume that the bidding transaction costs of the two directions are the same. User w_{0} transfers payment to user w_{6} . Based on the truthful routing mechanism proposed in [15], we can illusrate the differential privacy attack. The path with the lowest bidding transaction cost is w_{0}\rightarrow w_{1}\rightarrow w_{2}\rightarrow w_{3}\rightarrow w_{6} . In PCN, the sender does not need to pay for itself, thus the bidding transaction costs of the channels < w_{0}, \; w_{1} > , < w_{0}, \; w_{4} > , and < w_{0}, \; w_{5} > do not effect the route selection. As the user w_{5} changes the bidding transaction cost of channel < w_{5},\; w_{6} > from 10 to 7, then the shortest path changes to w_{0}\rightarrow w_{5}\rightarrow w_{6} , and user w_{5} infers the sum of the bidding transaction costs of channels < w_{1}, \; w_{2} > , < w_{2}, \; w_{3} > , and < w_{3}, \; w_{6} > is between 7 and 10. After many rounds, user w_{5} might narrow down the range of the sum of the bidding transaction costs of channels < w_{1}, \; w_{2} > , < w_{2}, \; w_{3} > , and < w_{3}, \; w_{6} > , and even infer the exact value. With the similar operation, user w_{5} can change the bidding transaction cost of channel < w_{5}, \; w_{3} > or channel < w_{5}, \; w_{4} > . At last, user w_{5} could obtain the bidding transaction costs of the channels < w_{1}, \; w_{2} > , < w_{2}, \; w_{3} > , and < w_{3}, \; w_{6} > by modifying the bidding transaction costs of its channels. As the truthful mechanism is used, user w_{5} can infer the transaction costs of these channels.
3.3 Problem Formulation
The routing mechanism \mathcal{M} (T,\; {\boldsymbol{B}}) outputs a path l_{f} from the sender to the recipient, a winner set S_{f} , and a transaction fee profile {{p}}=(p_{1},\;p_{2},\;\ldots ,\;p_{|S_{f}|} ). Without loss of generality, we denote the path l_{f} as w_{0} \rightarrow w_{1} \rightarrow w_{2}\rightarrow \ldots \rightarrow w_{|S_{f}|} \rightarrow w_{|S_{f}|+1} , where w_{0}=s , w_{|S_{f}|+1}=d . The objective is minimizing the total cost of the winners. We refer this problem as the Cost Optimization Routing (COR) problem, which can be formulated as follows:
\begin{gathered} \mathrm{(COR)}: {\mathrm{ min}} \sum \limits_{i \in S_{f}} c_{i}\\{\rm s.t.}\ \sigma_{i,\,i+1} \geqslant (t_{i,\,i+1}+ \sigma_{i+1,\,i+2}), \forall i \in \{ 0,\,1,\,\ldots ,\,\vert S_{f}\vert -1 \} , \end{gathered} (2) \sigma_{i,\,i+1} \geqslant t_{i,\,i+1},\, i = |S_{f}| , (3) r_{i,\,i+1} \geqslant (g+ \sum\nolimits_{j=i+1}^{|S_{f}|}p_{j}),\, \forall i \in \{ 1,\,\ldots ,\,|S_{f}|-1\} , (4) r_{i,\,i+1} =g,\, i = |S_{f}| . (5) Constraint (2) ensures that the HTLC tolerance of current payment channel is no smaller than the sum of its transaction time and the tolerance of successive payment channel. Constraint (3) ensures that the HTLC tolerance of the last payment channel in l_{f} is no smaller than its transaction time. Constraint (4) ensures that the channel capacity of the payment channel is enough to transfer the sum of the payment and accumulate transaction fees for the successive winners. Constraint (5) ensures that the channel capacity of the last payment channel in l_{f} is enough to transfer the payment.
3.4 Desirable Properties
Our objective is to design the PCN routing mechanism satisfying the following desirable properties:
Truthfulness. A mechanism is truthful if any user's utility is maximized when it bids the transaction cost, no matter what others submit.
Individual Rationality. A routing mechanism is individually rational if each user has a non-negative utility while bidding transaction cost, i.e., u_{i} \geqslant 0, \forall w_{i} \in W .
In addition, we take users’ transaction cost privacy-preserving into consideration.
Definition 1 (Personalized Local Differential Privacy[39]). Given a privacy requirement (B_{i}, \epsilon_{i}) of user w_{i} , a randomized mechanism \mathcal{M} satisfies \epsilon_{i} personalized local differential privacy if and only if for all b_{i}, b_{i}'\in B_{i} and any possible output b^* \in Range(\mathcal{M}) :
\mathrm{Pr}(\mathcal{M}(b_{i}) = b^*) \leqslant \mathrm{e}^{\epsilon_{i}}\mathrm{Pr}(\mathcal{M}(b_{i}') = b^*). Definition 2 (Differential Privacy[40]). A randomized mechanism \mathcal{M} satisfies \epsilon differential privacy if and only if for all x,\,x'\in \mathcal{X} and any possible output Z \in Range(\mathcal{M}) :
\mathrm{Pr}(\mathcal{M}(x) = Z) \leqslant \mathrm{e}^{\epsilon}\mathrm{Pr}(\mathcal{M}(x') = Z). Definition 3 ( \ell_{1} -Sensitivity[17]). The \ell_{1} -sensitivity of a function f : \mathbb{N}^{|x|} \rightarrow \mathbb{R}^ {k} is :
\Delta f=\mathrm{max}_{x,y \in \mathbb{N}^{|x|}, ||x-y||_{1} = 1} ||f(x)-f(y)||_{1}. In the context of PCN routing, we set \Delta f=C_{\rm{max}} .
Definition 4 (Laplace Mechanism[40]). Given any function f : \mathbb{N}^{|x|} \rightarrow \mathbb{R}^ {k} , the Laplace mechanism is defined as:
\mathcal{M}(x, f(\cdot),\epsilon) = f(x) + (\eta_{1},\ldots ,\eta_{k}), where \eta_{i} are independent and identically distributed random variables drawn from Lap( {\Delta f}/{\epsilon} ).
Definition 5 (Laplace Distribution[40]). The Laplace distribution (centered at 0) with scale b is the the distribution with probability density function:
Lap(x|b) = \frac{1}{2b}\mathrm{exp}\left(-\frac{|x|}{b}\right). The variance of this distribution is 2b^2 . The Lap(b) can simply denote a random variable X \sim Lap(0,\,b) .
Theorem 1. (Parallel Composition[41]). Let B_{1}, B_{2},\;\ldots ,\;B_{n} be n arbitrary disjoint datasets. The composite algorithm obtained by applying each M_{i} on a corresponding B_{i} provides max(\epsilon_{i}) differential privacy.
Table 1 lists the frequently used notations in this paper.
Table 1. Frequently Used NotationsNotation Description n Number of users m Number of channels s Sender of the transaction request d Recipient of the transaction request g Payment of the transaction request W Set of users in PCN w_{i} User w_{i} {\boldsymbol{B}} Bid profile B_{i} Bid of the user w_{i} b_{ij}^{t} Bidding transaction cost of channel < lt; $$ i,\; j $> gt; $b_{l}^{t} Bidding transaction cost of path l \overline{b_{ij}^{t}} Obfuscated bidding transaction cost of channel < lt; $$ i,\; j $> gt; $\overline{b_{l}^{t}} Obfuscated bidding transaction cost of path l r_{ij} Channel capacity of channel < lt; $$ i,\; j $> gt; $t_{ij} Transaction time of channel < lt; $$ i,\; j $> gt; $\epsilon_{ij} Privacy budget of channel < lt; $$ i,\; j $> gt; $\sigma_{ij} HTLC tolerance of channel < lt; $$ i,\; j $> gt; $\eta_{ij} Laplace noise of channel < lt; $$ i,\; j $> gt; $b_{l} Bidding path cost of path l c_{i} Cost of user w_{i} c_{ij}^{t} Transaction cost of channel < lt; $$ i,\; j $> gt; $,c_{ij}^{p} Privacy cost of channel < lt; $$ i,\; j $> gt; $C_{\rm{max}} Maximum cost of a channel {{p}} Transaction fee profile p_{i} Transaction fee of user w_{i} L_{\mathcal{K}} Set of the top \mathcal{K} -restricted shortest paths \overline{b_{\mathcal{K}}} Set of the obfuscated bidding path cost of the top \mathcal{K} -restricted shortest paths S_{\mathcal{K}} Winner set of the top \mathcal{K} -restricted shortest paths l_{k} The k -th path in top \mathcal{K} -restricted shortest paths l_{k}^{v} Deviating path of the v -th user on the k -th path S_{k}^{v} Winner set of the deviating path of the v -th user on the k -th path \overline{b_{l_{k}}^{v}} Obfuscated bidding path cost of the deviating path of the v -th user on the k -th path w_{v}^{k} The v -th deviating user of the k -th path \overline{b_{l_{k}}} Obfuscated bidding path cost of the k -th path S_{k} Winner set of the k -th path l_{0} Path before the deviating user l_{f} Final path S_{f} Winner set of the final path p_{l_{f}} Transaction fee profile of winners in the final path l_{f} \alpha Coefficient to scale the value of privacy cost \gamma Approximation factor \delta Search precision 4. Personalized Privacy-Preserving Routing Mechanism
4.1 Design Rationale
Theorem 2. The COR problem is NP-hard.
Proof. We consider a special case of COR problem. Suppose that the channel capacity of every payment channel and the HTLC tolerance of the intermediate users can always be satisfied. We demonstrate that the special case of the COR problem belongs to NP firstly. Based on the special case of the COR problem, we can check whether the transaction time of the final path is not more than the HTLC tolerance of the sender, and check whether the total cost of the final path is at most C_{\mathrm{max}} .
Next, we prove that the special case of the COR problem is NP-hard by giving a polynomial time reduction from the NP-hard Restricted Shortest Path (RSP) problem[42].
We first give the instance of the RSP problem (denoted by A). For a graph G = (V,\;E) with the vertex set V = \{v_{1},\;v_{2},\;\ldots ,\;v_{n}\} and the edge set E , each edge < i,\; j > \;\in E has a length c_{ij} and a transition time t_{ij} . Let t(l) be the total transition time of path l . For a given value T , the question is whether there exists a path from vertex s to vertex d with total cost no more than C_{\mathrm{max}} , such that t(l) \leqslant T .
Then, we consider a corresponding instance of the special case of the COR problem (denoted by B). For a PCN G = (V,\;E) with the user set V = \{w_{1}, \;w_{2},\;\ldots , w_{n}\} and the payment channel set E , each channel < i,\; j > \;\in E has a cost ({c_i+c_j})/{2} and a transition time t_{ij} . Let t(l) be the total transition time of path l . For a given value \sigma_{s,\,s+1} , the question is whether there exists a path from sender s to recipient d with total cost no more than C_{\mathrm{max}} , such that t(l)\leqslant\sigma_{s,\,s+1} , where s+1 is the next user of sender s in path l .
This reduction from A to B ends in polynomial time. We can simply see that q is a solution of A if and only if q is a solution of B.
Since the special case of COR problem is NP-hard, the COR problem is NP-hard.
□ In order to solve the problem, we need to compare any pair of paths to find the path with the largest probability of having the lowest path cost. However, we cannot find all paths in polynomial time since the COR problem is NP-hard. Therefore, we first obtain the top \mathcal{K} -restricted shortest paths, and then the path comparison is executed among the top \mathcal{K} -paths. The top \mathcal{K} -restricted shortest path problem can be solved approximately. Thus, we can compare any two paths among the top \mathcal{K} -restricted shortest paths to find the final path. At last, we calculate the transaction fee of each user in the path to satisfy the properties of truthfulness and individual rationality.
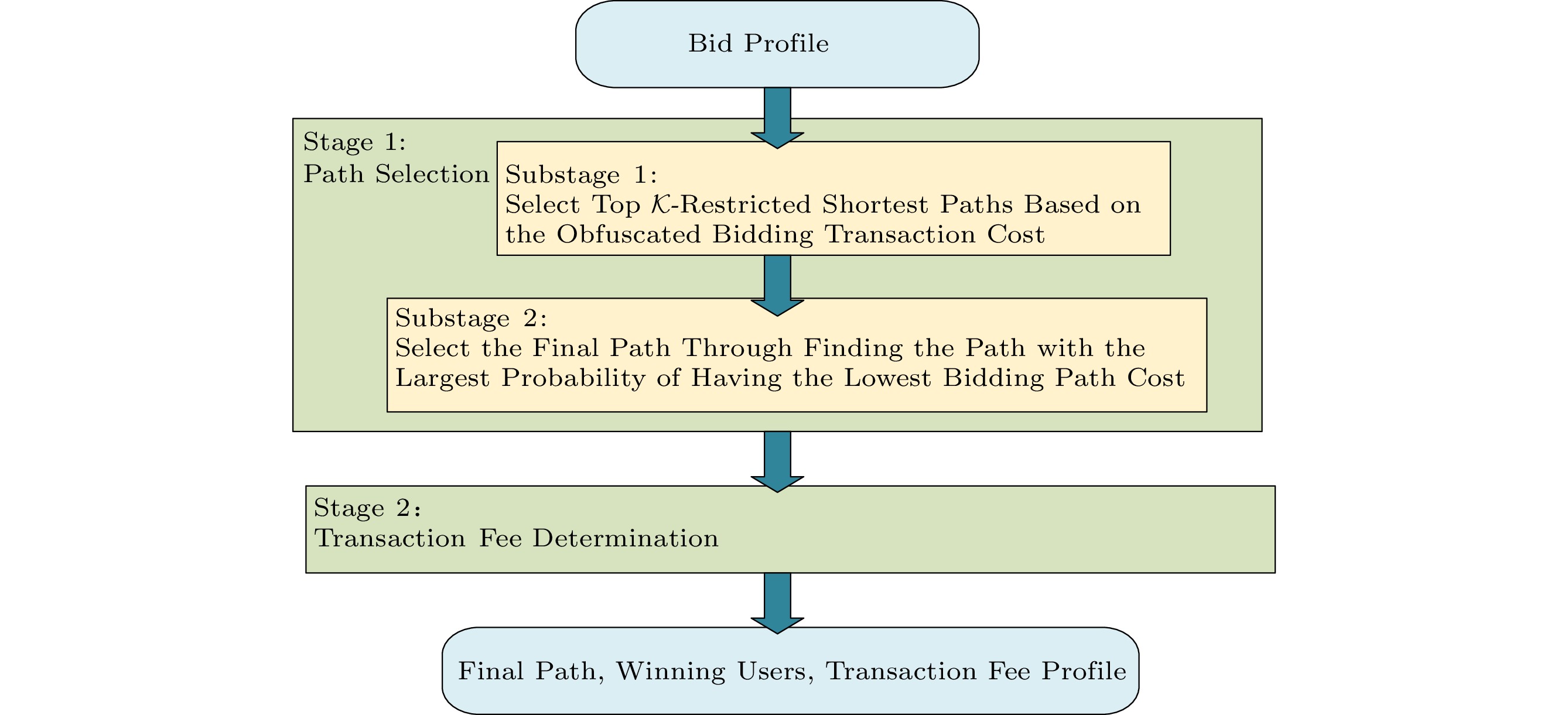
Overall, P ^3 RM consists of a path selection stage and a transaction fee determination stage, and the path selection stage consists of two substages: the top \mathcal{K} -restricted shortest path selection and the final path selection. The flowchart of the high-level overview of the proposed mechanism is illustrated in Fig.5.
The proposed mechanism P ^3 RM has four novelties. First, we propose the personalized differential privacy protection method to protect the transaction cost of the users based on the Laplace mechanism. Second, due to the COR problem is NP-hard, it cannot find the final path in polynomial time. We integrate the \mathcal{K} -shortest path selection algorithm and the restricted shortest path selection algorithm to narrow the search space. By adjusting the size of \mathcal{K} , the shortest path can be included in the top \mathcal{K} -restricted shortest paths to ensure the reliability of the algorithm. Third, the obfuscated bidding transaction cost of each user contains the Laplace noise, and it is hard to find the shortest path in the top \mathcal{K} -restricted shortest paths. We propose the path comparison algorithm, which can find the path that has the largest probability of having the lowest bidding path cost. Fourth, we use the binary search to find the critical value of transaction fee for each winner, which can ensure the truthfulness and individual rationality.
4.2 \mathcal{K} -Restricted Shortest Path Selection Algorithm
The top \mathcal{K} -restricted shortest path ( \mathcal{K} -RSP) problem is to find the top \mathcal{K} -restricted shortest paths with the lowest obfuscated bidding path cost. \mathcal{K} \geqslant 1 is a predefined parameter, which is related to the scale of the network. Generally, a larger PCN has more possible paths from the sender to the recipient, and a larger \mathcal{K} will be set to maintain the low cost of the final path. If there are no \mathcal{K} -restricted paths for the transaction, we can reduce the value of \mathcal{K} or abandon this transaction straightforwardly. Each selected path needs to satisfy the channel capacity and the HTLC tolerance constraints. Since we do not know the transaction fee of each user before the transaction fee determination stage, we use the maximum cost of the channel C_{\rm{max }} as the transaction fee of each payment channel. Since p_{i} \leqslant C_{\rm{max}} , \forall w_{i} \in W , the channel capacity constraint is always effective. The \mathcal{K} -RSP problem can be formulated as follows:
\begin{gathered} (\mathcal{K}-\mathrm{RSP}): {\mathrm {min}} \sum \nolimits_{l_{k} \in L_{\mathcal{K}}} \overline{b_{l_{k}}} \\ {\rm s.t.}\ \sigma_{i,\,i+1} \geqslant (t_{i,\,i+1}+ \sigma_{i+1,\,i+2}),\, \forall i \in \{ 0,\,1,\,\ldots ,\,|S_{k}| -1 \} ,\end{gathered} (6) \sigma_{i,\,i+1} \geqslant t_{i,\,i+1},\, i = |S_{k}| , (7) r_{i,\,i+1} \geqslant (g+ (|S_{k}|-(i+1))C_{\mathrm{max}}),\, \forall i \in \{ 1,\,\ldots ,\,|S_{k}|-1\} , (8) r_{i,\,i+1} =g,\, i = |S_{k}| . (9) Given the number of the restricted shortest paths \mathcal{K} , the objective of the \mathcal{K} -RSP problem is to find the first \mathcal{K} shortest paths under the constraints. Constraint (6) ensures that the HTLC tolerance of the current payment channel is no smaller than the sum of its transaction time and the HTLC tolerance of the successive payment channels. Constraint (7) ensures that the HTLC tolerance of the last payment channel in l_k is no smaller than its transaction time. Due to the transaction fee of winners is not determined, we use the maximum cost of the channel to replace the transaction fee. Constraint (8) ensures that the channel capacity of the payment channel is enough to transfer the sum of the payment and the accumulate maximum cost for the successive winners. Constraint (9) ensures that the channel capacity of the last payment channel in l_k is enough to transfer the payment.
We adopt the Yen's algorithm[43] to solve the \mathcal{K} -RSP problem. In [43], the selection of each path is based on the Dijkstra algorithm. However, each feasible PCN path should be constrained by the HTLC tolerance and the channel capacity. To solve this issue, we enhance the restricted shortest path algorithm[44] by considering the constraints of the HTLC tolerance and the channel capacity to select each path. Then, we use the Yen's algorithm to iteratively select the top \mathcal{K} -restricted shortest paths.
We use the function DCLC (G,\;s,\;d,\;g,\;\gamma) to find the restricted shortest path for the transaction request with payment g from sender s to recipient d on network G , where \gamma is the approximation factor, \gamma > 0 . DCLC compares the cost (the sum of the obfuscated bidding transaction cost and the privacy cost in this paper) of current node and its neighbor nodes to the sender, and selects a path with the lowest cost to update the next hop and the cost, which are stored in current node. When the recipient has been found, HTLC checks whether the time constraint (the HTLC tolerance of the sender in this paper) can be met. If the time constraint is met, it means that the shortest path has been found. We have added the HTLC tolerance and the channel capacity constraints when we execute the cost comparison to ensure that the shortest path is feasible. The approximation factor \gamma affects the precision of the path cost and the time complexity of DCLC. Hence, the determination of \gamma depends on the balance of the performance and the time complexity of the algorithm.
Let \overline{b_{l}} be the obfuscated bidding path cost of path l , which can be calculated as:
\overline{b_{ l }} =\sum\nolimits_{<i,\; j>\;\in l}\overline{b_{ij}}=(\sum\nolimits_{<i,\; j>\;\in l}\overline{b_{ij}^{t}}) + c_{l }^{p}. Let L_{\mathcal{K}} be the set of the top \mathcal{K} -restricted shortest paths. Let \overline{b_{\mathcal{K}}} and S_{\mathcal{K}} be the corresponding obfuscated bidding path cost and the winners of the top \mathcal{K} -restricted shortest paths, respectively.
The top \mathcal{K} -restricted shortest path selection ( \mathcal{K} -SP) is illustrated in Algorithm 1, which selects the shortest path iteratively by deviating the nodes and paths until the top \mathcal{K} -restricted shortest paths are found. Since the algorithm is executed by the sender, the payment g and the recipient d are chosen as the input of Algorithm 1. We first use DCLC (G,\;s,\;d,\;g, \gamma) to find the first path l_{1} (line 2), and then we find the remaining ( \mathcal{K}-1 ) paths through while-loop (lines 3–20). Given the k -th path l_{k} , we traverse all the users in order on this path (lines 5–15). If the traversed user w_{v}^{k} is not the sender, then we remove its predecessor w_{v-1}^{k} from the network, and add the payment channel with its predecessor into l_{0} , which is used to save the path before the deviating node (lines 6–8). Here, operation \biguplus represents the assembling of two paths. The payment channel connecting w_{v}^{k} and w_{v+1}^{k} is removed from the network (line 9). Then, we call DCLC (G^{'},\;w_{v}^{k},\;d,\;g,\;\gamma) to find the restricted shortest path for the transaction request with payment g from the deviating user w_{v}^{k} to the recipient d on the new network G^{'} , and the result is denoted by (l_{k}^{v},\;\overline{b_{l_{k}}^{v}},\;S_{k}^{v}) (line 10). If we can find the feasible deviating path, we assemble path l_{0} and path l_{k}^{v} , and put the assembled path into the candidate path set tem (lines 11–14). When all users on l_{k} are traversed, we choose the path with the lowest obfuscated bidding path cost in tem as the ( k+1 )-th path (lines 16, 17). Then, we remove the ( k+1 )-th path from tem and add it into the set of the top \mathcal{K} -restricted shortest paths (lines 18, 19). Finally, we return L_{\mathcal{K}} , \overline{b_{\mathcal{K}}} and S_{\mathcal{K}} (line 21).
Theorem 3. \mathcal{K} -SP is ( 1+\gamma )-approximation, where \gamma > 0 is the approximation factor.
Proof. In [44], for any given \gamma>0 , DCLC gives ( 1+\gamma )-approximation for each restricted shortest path selection in L_{\mathcal{K}} . The \mathcal{K} -shortest path selection algorithm provides the optimal solution. Thus, the approximation ratio of \mathcal{K} -SP is ( 1+\gamma ).
□ 4.3 Final Path Selection
Algorithm 1 finds the top \mathcal{K} -restricted shortest paths based on the obfuscated bids. However, it is difficult to find the path with the minimum bidding path cost since the sender does not know the original bidding transaction cost of the users. To solve this issue, we transform the problem to find the path with the largest probability of having the lowest bidding path cost.
Algorithm 1. \mathcal{K} -SP Input: network G , path number \mathcal{K} , payment g , approximation factor \gamma . 1: k\leftarrow 1 ; tem \leftarrow \varnothing ; L_{\mathcal{K}}\leftarrow \varnothing ; \overline{b_{\mathcal{K}}} \leftarrow \varnothing ; S_{\mathcal{K}} \leftarrow \varnothing ; 2: (l_{k},\; \overline{b_{l_{k}}},\; S_{k}) \leftarrow {DCLC}(G,\; s,\; d,\; g,\; \gamma) ; 3: while k \leqslant \mathcal{K} do 4: l_{0} \leftarrow \varnothing ; W^{'} \leftarrow W ; E^{'} \leftarrow E ; 5: for v=0 to \vert S_{k} \vert -1 do 6: if v \geqslant 1 then 7: W^{'} \leftarrow W^{'} \backslash \lbrace w_{v-1}^{k} \rbrace ; l_{0} \leftarrow l_{0}\biguplus < v-1,v > ; 8: end if 9: E^{'} \leftarrow E^{'} \backslash \lbrace < v,\;v+1 > \rbrace ; G^{'} \leftarrow (W^{'}, \;E^{'}) ; 10: (l_{k}^{v},\; \overline{b_{l_{k}}^{v}},\; S_{k}^{v}) \leftarrow {DCLC}(G^{'},\; w_{v}^{k},\; d,\; g,\; \gamma) ; 11: if l_{k}^{v} \neq \varnothing then 12: l_{k}^{v} \leftarrow l_{0} \biguplus l_{k}^{v} ; 13: tem \leftarrow tem \bigcup \lbrace l_{k}^{v},\;\overline{b_{l_{k}}^{v}},\;S_{k}^{v}\rbrace ; 14: end if 15: end for 16: k \leftarrow k+1 ; 17: (l_{k}^{v},\;\overline{b_{l_{k}}^{v}},\;S_{k}^{v}) \leftarrow \mathop{\arg\min}_{{({l_{k}^{v}}^{'},\;{\overline{b_{l_{k}^{v}}}}',\;{S_{k}^{v}}^{'})}\in tem} \overline{b_{l_{k}^{v}}}' ; 18: tem \leftarrow tem \backslash \lbrace l_{k}^{v},\;\overline{b_{l_{k}}^{v}},\;S_{k}^{v} \rbrace ; 19: L_{\mathcal{K}} \leftarrow L_{\mathcal{K}} \bigcup \lbrace l_{k}^{v} \rbrace ; \overline{b_{\mathcal{K}}} \leftarrow \overline{b_{\mathcal{K}}} \bigcup \lbrace \overline{b_{l_{k}}^{v}} \rbrace ; S_{\mathcal{K}} \leftarrow S_{\mathcal{K}} \bigcup \lbrace S_{k}^{v} \rbrace ; 20: end while 21: return ( L_{\mathcal{K}} , \overline{b_{\mathcal{K}}} , S_{\mathcal{K}} ); Without loss of generality, we consider any two paths l_{\varphi}\in L_{\mathcal{K}} and l_{\xi} \in L_{\mathcal{K}} with \vert S_{\varphi} \vert and \vert S_{\xi} \vert intermediate users, respectively. Then, the obfuscated bidding path cost of l_{\varphi} and l_{\xi} can be calculated as:
\overline{b_{ l_{\varphi} }} =\sum\nolimits_{<i,\; j>\;\in l_{\varphi}}\overline{b_{ij}}=(\sum\nolimits_{<i,\; j>\;\in l_{\varphi}}\overline{b_{ij}^{t}} )+ c_{l_{\varphi} }^{p}, \qquad \overline{b_{ l_{\xi} }} =\sum\nolimits_{<i^{'},\,j^{'}>\;\in l_{\xi}}\overline{b_{i^{'}j^{'}}}=(\sum\nolimits_{<i^{'},\,j^{'}>\;\in l_{\xi}}\overline{b_{i^{'}j^{'}}^{t}} )+ c_{l_{\xi} }^{p}, where c_{l_{\varphi} }^{p} and c_{l_{\xi} }^{p} are total privacy cost of the users on path l_{\varphi} and l_{\xi} , respectively.
Using the Laplace mechanism, the obfuscated bidding transaction cost of the payment channel < i,\; j >\;\in l_{\varphi} and < i^{'},\,j^{'} >\;\in l_{\xi} can be calculated as:
\overline{b_{ ij }^{t}} =b_{ ij }^{t} + \eta_{ij}, \eta_{ij}\sim{\mathrm{Lap}\left(0,\frac{C_{\mathrm{max}}}{\epsilon_{ij}}\right)}, \overline{b_{ i^{'}j^{'} }^{t}} =b_{ i^{'}j^{'} }^{t} + \eta_{i^{'}j^{'}}, \eta_{i^{'}j^{'}}\sim{\mathrm{Lap}(0,\frac{C_{\mathrm{max}}}{\epsilon_{i^{'}j^{'}}})}, where \eta_{ij} and \eta_{i^{'}j^{'}} are variables that follow the Laplace probability density function (pdf).
f(\eta_{ij})=\dfrac{\epsilon_{ij}}{2C_{\mathrm{max}}}\mathrm{e}^{\dfrac{-(\epsilon_{ij}\vert \eta_{ij} \vert)}{C_{\mathrm{max}}}}, f(\eta_{i^{'}j^{'}})=\dfrac{\epsilon_{i^{'}j^{'}}}{2C_{\mathrm{max}}}\mathrm{e}^{\dfrac{-(\epsilon_{i^{'}j^{'}}\vert \eta_{i^{'}j^{'}} \vert)}{C_{\mathrm{max}}}}. The bidding path cost of two paths are:
b_{ l_{\varphi} }^{t}=\sum\nolimits_{<i,\; j>\;\in l_{\varphi}}b_{ij} ^{t}, b_{ l_{\xi} }^{t}=\sum\nolimits_{<i^{'},\,j^{'}>\;\in l_{\xi}}b_{i^{'}j^{'}}^{t}. Then, the probability that b_{l_{\varphi} } is no larger than b_{l_{\xi} } is:
\begin{aligned} &\quad\;\, \mathrm{Pr}(b_{ l_{\varphi} } \leqslant b_{ l_{\xi} })=\mathrm{Pr}( b_{ l_{\varphi} }^{t}+c_{l_{\varphi} }^{p} \leqslant b_{ l_{\xi} }^{t} + c_{l_{\xi} }^{p}) \\ &=\mathrm{Pr}( \overline{b_{ l_{\varphi} }^{t}} -\eta_{l_{\varphi}} + c_{l_{\varphi} }^{p} \leqslant \overline{b_{ l_{\xi} }^{t}} -\eta_{l_{\xi}} + c_{l_{\xi} }^{p}) \\ &=\mathrm{Pr}(\overline{b_{ l_{\varphi} }} -\overline{b_{ l_{\xi} }} \leqslant \eta_{l_{\varphi}}-\eta_{l_{\xi}}), \nonumber \end{aligned} where \eta_{l_{\varphi}}=\sum_{<i,\; j>\;\in l_{\varphi}}\eta_{ij} and \eta_{l_{\xi}}=\sum_{<i^{'},\,j^{'}>\;\in l_{\xi}}\eta_{i^{'}j^{'}} . b_{ l_{\varphi} } and b_{ l_{\xi} } are the bidding path cost of l_{\varphi} and l_{\xi} , respectively. It can be viewed as a probability problem about two-dimensional continuous variables ( \eta_{l_{\varphi}},\; \eta_{l_{\xi}} ) in the plane set D :
D=\lbrace{ ( \eta_{l_{\varphi}},\; \eta_{l_{\xi}})|\eta_{l_{\varphi}}-\eta_{l_{\xi}} \geqslant \overline{b_{ l_{\varphi} }} -\overline{b_{ l_{\xi} }}}\rbrace. (10) We use the double integral operation to solve this problem:
\mathrm{Pr}(\overline{b_{ l_{\varphi} }} -\overline{b_{ l_{\xi} }} \leqslant \eta_{l_{\varphi}}-\eta_{l_{\xi}} ) = \int\int_{{D}}{f}(\eta_{l_{\varphi}},\; \eta_{l_{\xi}})\mathrm{d}\eta_{l_{\varphi}}\mathrm{d}\eta_{l_{\xi}}, where f(\eta_{l_{\varphi}}, \eta_{l_{\xi}}) is the joint probability distribution function of (\eta_{l_{\varphi}}, \eta_{l_{\xi}}) .
Since the Laplace noise of each user in two different paths is independent, we have:
\begin{split} \int\int_{D}&f(\eta_{l_{\varphi}}, \eta_{l_{\xi}})\mathrm{d}\eta_{l_{\varphi}}\mathrm{d}\eta_{l_{\xi}} = \int\int_{{D}}{f}(\eta_{l_{\varphi}}){f}( \eta_{l_{\xi}})\mathrm{d}\eta_{l_{\varphi}}\mathrm{d}\eta_{l_{\xi}}\\ &=\int_{-\infty}^{+\infty}\int_{-\infty}^{\eta_{l_{\varphi}}-(\overline{b_{ l_{\varphi} }} -\overline{b_{ l_{\xi} }})}f(\eta_{l_{\varphi}})f( \eta_{l_{\xi}})\mathrm{d}\eta_{l_{\varphi}}\mathrm{d}\eta_{l_{\xi}}. \end{split} (11) To sum up, if \mathrm{Pr}(b_{ l_{\varphi} } \leqslant b_{ l_{\xi} }) > 1/2 , it indicates that the bidding path cost of l_{\varphi} is smaller than that of l_{\xi} with a higher probability. We can compare any two paths to find the path with the largest probability of having the lowest bidding path cost.
Remark. The obfuscated bidding transaction cost processed by the Laplace mechanism could be negative, though the probability of negative is very small since we have carefully set the sensitivity of the Laplace mechanism as C_{\mathrm{max}} . If the user adds negative noise in the bidding transaction cost, it may lead to negative bidding transaction cost. Hence, the negative obfuscated bidding transaction cost is reasonable. Even if the negative obfuscated bidding transaction cost leads to the negative obfuscated bidding path cost, (11) can be calculated, and the value of (11) monotonically decreases with respect to (\overline{b_{ l_{\varphi} }} -\overline{b_{ l_{\xi} }}) . Therefore, the negative obfuscated bidding transaction cost will not affect the correctness and feasibility of the path comparison.
4.4 Routing Mechanism Design and Analysis
As illustrated in Algorithm 2, P ^3 RM consists of a path selection stage and a transaction fee determination stage.
Algorithm 2. P ^3 RM Input: network G , path number \mathcal{K} , payment g , approximation factor \gamma . // Path Selection 1: (L_{\mathcal{K}},\overline{b_{\mathcal{K}}},S_{\mathcal{K}}) \leftarrow \mathcal{K} -{\rm SP} (G,\mathcal{K},g,\gamma) ; 2: l_{\mathrm{min}}\leftarrow l_{1} ; S_{f} \leftarrow \varnothing ; 3: for k=2 to \mathcal{K} do 4: if \mathrm{Pr}(b_{ l_{k} }\leqslant b_{ l_{\mathrm{min}} }) > \dfrac{1}{2} then l_{\mathrm{min}} \leftarrow l_{k} ; 5: end for 6: l_{f} \leftarrow l_{\mathrm{min}} ; S_{f} \leftarrow S_{l_{\mathrm{min}}} ; // Transaction Fee Determination 7: for each w_{i} \in S_{f} do p_{i} \leftarrow 0 ; 8: for each w_{i} \in S_{f} do 9: W^{'} \leftarrow W\backslash \lbrace w_{i}\rbrace ; E^{'} \leftarrow E \backslash \bigcup_{{j}\in N_{i}}\lbrace < i,\; j > \rbrace ; 10: G^{'} \leftarrow (W^{'},E^{'}) ; 11: (L_{\mathcal{K}}^{'},{\overline{b_{\mathcal{K}}}}{'},S_{\mathcal{K}}^{'}) \leftarrow \mathcal{K} -SP (G^{'},\mathcal{K},g,\gamma) ; 12: p_{i}^{\mathrm{up}} \leftarrow \dfrac{ \sum\nolimits_{l_{k}^{'} \in L_{\mathcal{K}}^{'}}\overline{b_{l_{k}^{'}}}-(\sum\nolimits_{l_{k} \in L_{\mathcal{K}}}\overline{b_{l_{k}}}-num_{i}\overline{b_{ij}})}{num_{i}} ; 13: let p_{i} be the lowest price calculated through binary search in range [\overline{b_{ij}}, p_{i}^{\mathrm{up}}] such that the user w_{i} is not in the final path; 14: end for 15: return ( l_{f} , {{p}} , S_{f} ); In the path selection stage, we first call Algorithm 1 to find the top \mathcal{K} -restricted shortest paths (line 1), and then find the path that has the largest probability of having the lowest bidding path cost as the final path (lines 2–6).
In the transaction fee determination stage, we use the Myerson's Theorem[45] and binary search to calculate the critical value. For each winner w_{i} \in S_{f} , we find the top \mathcal{K} -restricted shortest paths over W \backslash \{ w_{i}\} , and the set of selected paths is denoted by L_{\mathcal{K}}^{'} (line 11). We compute the difference of the total obfuscated bidding path cost of the \mathcal{K} -restricted shortest paths with and without user w_{i} . We divide the price averagely over the number of paths that includes user w_{i} (denoted by num_{i} ), and denote the average price by p_{i}^{\mathrm{up}} (line 12). We will prove that this price is an upper bound of critical value for user w_{i} later. Then we binary search the range [\overline{b_{ij}}, p_{i}^{\mathrm{up}}] to find the lowest price such that user w_{i} does not exist in the final path (line 13), where \overline{b_{ij}} is w_{i} 's obfuscated bidding cost in l_{f} . We will prove that this price is a critical payment for user w_{i} later.
In the following, we present theoretical analysis, demonstrating that P ^3 RM can achieve the desirable properties.
Lemma 1. The time complexity of P ^{3} RM is O(\mathcal{K}mn^{3} ({\mathrm{ loglog}}n+({1}/{\gamma})){ \mathrm{log}}({ C_{{\mathrm{max}}} }/{\delta})) .
Proof. We first analyze the time complexity of \mathcal{K} -SP, which is dominated by finding the deviating path for each user in the current selected path (line 10). Based on [44], DCLC takes O(mn({\rm loglog}n+ ({1}/{\gamma}))) time. Since there are at most n users in a path, finding all deviating paths for all users takes O(mn^{2} ({\rm loglog}n+({1}/{\gamma}))) time. The while-loop (line 3) runs \mathcal{K} times. Thus, the time complexity of \mathcal{K} -SP is O(\mathcal{K}mn^{2} ({\rm loglog}n+({1}/{\gamma}))) . Next, we analyze the time complexity of P ^3 RM. It is clear that the time complexity of P ^3 RM is dominated by the binary search (line 13). If we set the search precision as \delta , then the time complexity of binary search is O({\rm log}(({p_{i}^{\mathrm{up}}-\overline{b_{ij}}})/{\delta})) . Since the difference of any two bidding prices is no more than C_{\mathrm{max}} , the time complexity of the binary search is bounded by O({\rm log}({ C_{\mathrm{max}} }/{\delta})) . In each iteration of binary search, a path selection stage is performed. Thus, calculating the critical value for any winner takes O(\mathcal{K}mn^{2} ({\rm loglog}n+({1}/{\gamma})){\rm log}({ C_{\mathrm{max}} }/{\delta})) time. Since there are at most n winners, the time complexity of P ^3 RM is O(\mathcal{K}mn^{3} ({\rm loglog}n+({1}/{\gamma})){\rm log}({ C_{\mathrm{max}} }/{\delta})) .
□ Before analyzing the truthfulness of P ^3 RM, we first introduce the Myerson's Theorem[45] and the definition of \mathcal{P} -truthfulness.
Theorem 4. An auction mechanism is truthful iff:
● Monotone Allocation: Given users’ bid profile \boldsymbol{B} , if user w_{i} wins by bidding b_{i} , it also wins by bidding b_{i}^{'} \leqslant b_{i} .
● Critical Value: There exists a critical value for each user w_{i} \in W such that it would not win the auction if it bids higher than this value.
Definition 6 ( {\mathcal{P}} -Truthfulness). A mechanism is \mathcal{P} -truthful if any user's utility is maximized with probability at least \mathcal{P} when it bids the transaction cost, no matter what others submit.
Lemma 2. P ^{3} RM is 1/2-truthful.
Proof. We first analyze the monotonicity of the path selection of P ^3 RM. Note that both the top \mathcal{K} -restricted shortest path selection substage and the final path selection substage are monotone if we select the path based on the bidding transaction cost rather than the obfuscated bidding transaction cost. Thus, we need to calculate the probability of monotonicity on the obfuscated bidding transaction cost. Without loss of generality, we consider a bidding transaction cost {b_{ij}^{t}}' \leqslant b_{ij}^{t} , then the probability of \overline{{b_{ij}^{t}}'} \leqslant \overline{b_{ij}^{t}} can be calculated as:
\begin{split} &\quad\;\, \mathrm{Pr}(\overline{{b_{ij}^{t}}'}\leqslant \overline{b_{ij}^{t}})=\mathrm{Pr}( {b_{ij}^{t}}'+{\eta_{ij}}' \leqslant b_{ij}^{t}+\eta_{ij})\\ &=\mathrm{Pr}({b_{ij}^{t}}'-b_{ij}^{t} \leqslant \eta_{ij}-{\eta_{ij}}'). \end{split} (12) According to (10), we can get the two-dimensional continuous variables ( \eta_{ij} , {\eta_{ij}}' ) in the plane set D, i.e., D=\lbrace{ ( \eta_{ij}, {\eta_{ij}}')|\eta_{ij}-{\eta_{ij}}' \geqslant {b_{ij}^{t}}'-b_{ij}^{t}\rbrace} . Hence, we can use double integral operation to solve (12):
\begin{split} &\mathrm{Pr}({b_{ij}^{t}}'-b_{ij}^{t} \leqslant \eta_{ij}-{\eta_{ij}}')=\int\int_{D}f(\eta_{ij})f({\eta_{ij}}')\mathrm{d}{\eta_{ij}}'\mathrm{d}\eta_{ij}\\ &=\int_{-\infty}^{+\infty}\int_{-\infty}^{\eta_{ij}-({b_{ij}^{t}}'-b_{ij}^{t} )}f(\eta_{ij})f({\eta_{ij}}')\mathrm{d}{\eta_{ij}}'\mathrm{d}\eta_{ij}. \\[-1pt] \end{split} (13) We set \Delta = {b_{ij}^{t}}'-b_{ij}^{t} . Then, the result of (13) is as follows:
\begin{aligned} \mathrm{Pr}({b_{ij}^{t}}'-b_{ij}^{t} \leqslant \eta_{ij}-{\eta_{ij}}')=1-\frac{1}{2}e^{\epsilon_{ij}\Delta}+\frac{\epsilon_{ij}\Delta}{4}e^{\epsilon_{ij}\Delta}. \end{aligned} (14) The function of (14) monotonically decreases with respect to \Delta when \Delta \leqslant 0 . The lowest probability is 1/2 when \Delta = 0 . Hence, \mathrm{Pr}(\overline{{b_{ij}^{t}}'}\leqslant \overline{b_{ij}^{t}}) \geqslant 1/2 . This means P ^3 RM is monotone with the probability at least 1/2. Specifically, the more the change of the bidding transaction cost is, the higher the probability of monotonicity is.
We next show that p_{i} is the critical value for user w_{i} in the sense that bidding higher than p_{i} could prevent user w_{i} from winning the auction. As shown in Algorithm 2, we set p_{i}^{\rm{up}} as the upper bound of critical value of user w_{i} . If user w_{i} bids \overline{b_{ij}} \geqslant p_{i} we have:
\begin{aligned} &\overline{b_{ij}} \geqslant \dfrac{ \sum\nolimits_{l_{k}^{'} \in L_{\mathcal{K}}^{'}}\overline{b_{l_{k}^{'}}}-(\sum\nolimits_{l_{k} \in L_{\mathcal{K}}}\overline{b_{l_{k}}}-\sum\nolimits_{<i,\; j>\;\in l_{k},l_{k}\in L_{\mathcal{K}}}\overline{b_{ij}})}{num_{i}} \\ &\Rightarrow num_{i}\overline{b_{ij}} \geqslant \sum\nolimits_{l_{k}^{'} \in L_{\mathcal{K}}^{'}}\overline{b_{l_{k}^{'}}}-(\sum\nolimits_{l_{k} \in L_{\mathcal{K}}}\overline{b_{l_{k}}}-num_{i}\overline{b_{ij}})\\ &\Rightarrow \sum\nolimits_{l_{k} \in L_{\mathcal{K}}}\overline{b_{l_{k}}} \geqslant \sum\nolimits_{l_{k}^{'} \in L_{\mathcal{K}}^{'}}\overline{b_{l_{k}^{'}}}. \nonumber \end{aligned} This means L_{\mathcal{K} } will be replaced by L_{\mathcal{K}}' since the total obfuscated bidding path cost of L_{\mathcal{K}}' is smaller than that of L_{\mathcal{K}} .
Supposing P ^3 RM is monotone, we can binary search the range [\overline{b_{ij}},\; p_{i}^{\rm{up}}] , and find the lowest price that user w_{i} is not in the final path. Obviously, this price is the critical value of user w_{i} . Since the probability of monotonicity is at least 1/2, we get the lemma.
□ Before analyzing the individual rationality of P ^3 RM, we introduce the definition of {\mathcal{P}} -Individual rationality.
Definition 7 ( {\mathcal{P}} -Individual Rationality[20]). A routing mechanism is \mathcal{P} -individually rational if each user w_{i} has a non-negative utility u_{i} with probability at least \mathcal{P} while bidding transaction cost, i.e., \mathrm{Pr}(u_{i} \geqslant 0) \geqslant \mathcal{P}, \forall w_{i} \in W .
Lemma 3. P ^{3} RM achieves 1/4-individual Rationality.
Proof. Based on (1), for any winner w_{i} , we have:
u_{i} = p_{i}-(c_{ij}^{t}+c_{ij}^{p}). Therefore, the probability of the winner receiving a non-negative utility can be converted to the probability of p_{i} larger than b_{ij}^{t}+c_{ij}^{p} , which is
\begin{split} &\mathrm{Pr}(p_{i}\geqslant c_{ij}^{t}+c_{ij}^{p} )\\\geqslant\ & \mathrm{Pr}(b_{ij}^{t}=c_{ij}^{t})\mathrm{Pr}(p_{i} \geqslant \overline{b_{ij}})\mathrm{Pr}(\overline{b_{ij}} \geqslant b_{ij}^{t}+c_{ij}^{p})\\=\ &\mathrm{Pr}(b_{ij}^{t}=c_{ij}^{t})\mathrm{Pr}(p_{i} \geqslant \overline{b_{ij}})\mathrm{Pr}(\overline{b_{ij}^{t}}+c_{ij}^{p} \geqslant b_{ij}^{t}+c_{ij}^{p})\\=\ &\mathrm{Pr}(b_{ij}^{t}=c_{ij}^{t})\mathrm{Pr}(p_{i} \geqslant \overline{b_{ij}})\mathrm{Pr}(b_{ij}^{t}+\eta_{ij} \geqslant b_{ij}^{t}). \end{split} \mathrm{Pr}(b_{ij}^{t}=c_{ij}^{t}) represents the probability of truthfulness. Based on Lemma 2, we have \mathrm{Pr}(b_{ij}^{t}=c_{ij}^{t}) \geqslant 1/2 . Since \overline{b_{ij}} is the lower bound of p_{i} , we have \mathrm{Pr}(p_{i} \geqslant \overline{b_{ij}})=1 . Moreover, it is obvious that \mathrm{Pr}(b_{ij}^{t}+\eta_{ij} \geqslant b_{ij}^{t}) = 1/2. Therefore, we have \mathrm{Pr}(p_{i}\geqslant c_{ij}^{t}+c_{ij}^{p} ) \geqslant 1/4 . In other words, \mathrm{Pr}(u_{i} \geqslant 0) \geqslant 1/4 .
□ Lemma 4. P ^{3} RM is \sum \nolimits_{i=0}^{q} \mathrm{max}(\epsilon_{i}) differential privacy, where q is the length of the final path, and \mathrm{max}(\epsilon_{i}) is the maximum privacy budget of all the payment channel for the user w_{i} .
Proof. b_{ij}^{t} is the bidding transaction cost of channel < i,\; j > . We use the Laplace mechanism to add noise to b_{ij}^{t} , i.e., \mathcal{M}(b_{ij}^{t} )=b_{ij}^{t}+\eta_{ij}, \eta_{ij} \sim \mathrm{Lap}(0, ({C_{\mathrm{max}}}/{\epsilon_{ij}})) . For any two bids B_{ij} and B_{ij}' , the output is the obfuscated bidding transaction cost \overline{b_{ij}^{t}} . We have:
\begin{split} &\quad\;\dfrac{\mathrm{Pr}(\mathcal{M}(B_{i})=\overline{b_{ij}^{t}})}{\mathrm{Pr}(\mathcal{M}(B_{i}')=\overline{b_{ij}^{t}})} = \dfrac{\mathrm{exp}(\dfrac{-\epsilon_{ij}|\overline{b_{ij}^{t}}-b_{ij}^{t}|}{C_{\mathrm{max}}})}{\mathrm{exp}(\dfrac{-\epsilon_{ij}|\overline{b_{ij}^{t}}-{b_{ij}^{t}}'|}{C_{\mathrm{max}}})}\\ &=\mathrm{exp}(\dfrac{\epsilon_{ij}(|\overline{b_{ij}^{t}}-{b_{ij}^{t}}'|-|\overline{b_{ij}^{t}}-b_{ij}^{t}|)}{C_{\mathrm{max}}})\\ &\leqslant \mathrm{exp}(\dfrac{\epsilon_{ij}|b_{ij}^{t}-{b_{ij}^{t}}'|}{C_{\mathrm{max}}}) \leqslant \mathrm{exp}(\epsilon_{ij}), \end{split} where the last inequation relies on the fact of |b_{ij}^{t}-{b_{ij}^{t}}'| \leqslant C_{\mathrm{max}} . Each user has more than one payment channel, and each channel is disjoint. We use \epsilon_{i} to denote the privacy budget of all the payment channels for user w_{i} . Based on Theorem 1, we have the obfuscated mechanism which satisfies \mathrm{max}(\epsilon_{i}) personalized local differential privacy for the user w_{i} .
After the noise is added to the bidding transaction cost, the restricted shortest path selection mechanism M is operated based on the obfuscated network. Let B and B' be two bid profiles that differ in any channel < i, \;j > 's obfuscated bidding transaction cost. We can get the path with the lowest obfuscated path cost as M is excuted. Let M({\boldsymbol{B}}) and M({\boldsymbol{B'}}) denote the path cost of the users in the shortest path selected by M based on B and B', respectively. For any shortest path l = (w_{0},\; w_{1},\; \ldots ,\; w_{q}) with length q , and the obfuscated bidding transaction cost of users in path l is \overline{b_l^{t}} = (\overline{b_{0}^{t}},\; \overline{b_{1}^{t}}, \;\ldots ,\; \overline{b_{q}^{t}}) , the mechanism can achieve differential privacy. We consider the relative probability of the restricted shortest path selection for given bid inputs B and B':
\begin{split} &\quad\;\dfrac{\mathrm{Pr}(M({\boldsymbol{B}})=\overline{b_{l}^{t}})}{\mathrm{Pr}(M({\boldsymbol{B'}})=\overline{b_{l}^{t}})} = \prod \nolimits_{i=0}^{q} \dfrac{\mathrm{exp}(\dfrac{-\epsilon_{i}|\overline{b_{i}^{t}}-b_{i}^{t}|}{C_{\mathrm{max}}})}{\mathrm{exp}(\dfrac{-\epsilon_{i}|\overline{b_{i}^{t}}-{b_{i}^{t}}'|}{C_{\mathrm{max}}})}\\ &=\prod \nolimits_{i=0}^{q} \mathrm{exp}(\dfrac{\epsilon_{i}(|\overline{b_{i}^{t}}-{b_{i}^{t}}'|-|\overline{b_{i}^{t}}-b_{i}^{t}|)}{C_{\mathrm{max}}})\\ &\leqslant \prod \nolimits_{i=0}^{q} \mathrm{exp}(\dfrac{\epsilon_{i}|b_{i}^{t}-{b_{i}^{t}}'|}{C_{\mathrm{max}}}) \\ & \leqslant \mathrm{exp}(\sum \limits_{i=0}\limits^{q} \mathrm{max}(\epsilon_{i})). \end{split} As a user has only one channel that can be selected as the wining payment channel, M satisfies \sum \nolimits_{i=0}^{q} \mathrm{max}(\epsilon_{i}) differential privacy.
Since the \mathcal{K} -restricted shortest paths have been selected, the final path is determined. Thus, the final path selection phase does not effect the differential privacy of P ^3 RM. In summary, P ^3 RM satisfies \sum \nolimits_{i=0}^{q} \mathrm{max}(\epsilon_{i}) differential privacy.
□ The above lemmas together prove the following theorem.
Theorem 5. The time complexity of P ^3 RM is O(\mathcal{K}mn^{3} ({\mathrm{ loglog}}n+({1}/{\gamma})){ \mathrm{log}}({ C_{{\mathrm{max}}} }/{\delta})) , and the mechanism achieves truthfulness with probability at least 1/2, individual rationality with probability at least 1/4, and \sum \nolimits_{i=0}^{q} {\mathrm{max}}(\epsilon_{i}) differential privacy, where n is the number of users, m is the number of channels, q is the length of the final path, and \mathrm{max}(\epsilon_{i}) is the maximum privacy budget of all payment channel for the user w_{i} .
Since P ^3 RM is not strictly truthful, we analyze the maximum gain a user can achieve by bidding untruthfully.
Lemma 5. For any user w_{i} \in W , if the user w_{i} loses by bidding truthfully, it may obtain the maximum gain p_{i}^{\mathrm{up}} - \left( c_{ij}^{t} + c_{ij}^{p} \right) when it wins by bidding untruthfully, where < i,\; j > is the winning channel when bidding untruthfully; if the user w_{i} wins by bidding truthfully, it may obtain the maximum gain c_{ij}^{p} - \eta_{ij} when it loses by bidding untruthfully, where < i,\; j > is the winning channel when bidding truthfully.
Proof. We consider the following two cases.
Case 1. User w_{i} loses by bidding truthfully, and thus u_{i}=0 .
Case 1.1. If the user w_{i} still loses by bidding untruthfully, nothing changes.
Case 1.2. If the user w_{i} wins by bidding untruthfully, the maximum transaction fee is p_i^{\mathrm{up}} based on the transaction fee determination rule of P ^3 RM. Thus, the maximum gain user w_{i} can achieve is {u_{i}' = p}_{i}^{\mathrm{up}} - \left( c_{ij}^{t} + c_{ij}^{p} \right) based on (1).
Case 2. User w_{i} wins by bidding truthfully, and thus u_{i} = p_{i} - \left( c_{ij}^{t} + c_{ij}^{p} \right) based on (1).
Case 2.1. If user w_{i} still wins by bidding untruthfully, nothing changes since the transaction fee determined by P ^3 RM does not depend on the bidding transaction cost of the user w_{i} .
Case 2.2. If user w_{i} loses by bidding untruthfully, we have u_i'=0 . If u_i<0 , user w_{i} can gain
\begin{split} &\quad\;\, u_i' - u_{i} = c_{ij}^{t} + c_{ij}^{p} - p_{i}\\ &\leqslant c_{ij}^{t} + c_{ij}^{p} - \overline{b_{ij}} = c_{ij}^{t} + c_{ij}^{p} - \left( {b_{ij}^{t} + \eta_{ij}} \right) = c_{ij}^{p} - \eta_{ij}, \end{split} where the inequality relies on the fact that \overline{b_{ij}} is the lower bound of p_i based on the transaction fee determination rule of P ^3 RM.
□ Since P ^3 RM is not of strict individual rationality, we analyze the maximum loss a user can incur by participating in the auction truthfully.
Lemma 6. For any user w_{i} \in W , the maximum loss user w_i can incur by participating in the auction truthfully is c_{ij}^{p} - \eta_{ij} , where < i,\; j > is the winning channel when bidding truthfully.
Proof. The loss only happens when user w_i wins with negative utility. In this case, the maximum loss of the user w_i is \left. {- u}_{i} = {- \left( p \right.}_{i} - \left( {c_{ij}^{t} + c_{ij}^{p}} \right) \right) = c_{ij}^{t} + c_{ij}^{p} - p_{i} \leqslant c_{ij}^{p} - \eta_{ij} .
□ 5. Performance Evaluation
5.1 Simulation Setup
We evaluate the performance of P ^3 RM based on the real-world datasets from the path-based transaction network Ripple
4 , which contains link creations, channel capacities, modifications, and transactions, from January 2013 to November 2016. For each instance of simulations, we randomly select a subgraph of the whole network. The parameter settings are listed in Table 2. We will vary the value of key parameters to explore the impacts of these parameters.Table 2. Parameter SettingsParameter Value n 150 c_{ij}^{t} Uniform distribution over (0, 1] \alpha 0.5 \epsilon_{ij} Uniform distribution over (0, 1] \sigma_{ij} Uniform distribution over [13, 15] t_{ij} Uniform distribution over [0.5,1] g [10,1\;000] C_{\mathrm{max}} 10 \mathcal{K} 9 \gamma 2 \delta 0.02 We compare P ^3 RM with following benchmark algorithms.
● DCLC[44]. DCLC finds the restricted shortest path and does not offer the privacy protection. Actually, it provides the upper bound of performance in terms of the path cost.
● Privacy-Preserving Routing Mechanism (P ^2 RM). The process of P ^2 RM is the same as that of P ^3 RM. The difference is that the privacy budget is set uniformly as 1 for all users in P ^2 RM.
5.2 Performance Metrics
We use the following metrics for performance evaluation.
Average Path Cost: average path cost over all accepted transaction requests.
Average Transaction Fee: average transaction fee over all accepted transaction requests.
Success Ratio: the ratio of accepted transaction requests.
Privacy Leakage (PL): given a mechanism \mathcal{M} , let B and {\boldsymbol{B}'} be two bid profiles, which only differ in one user's bid. Let \mathcal{M}({\boldsymbol{B}}) and \mathcal{M}({\boldsymbol{B}'}) denote the outcome of the selected path, respectively. The privacy leakage is defined as the Kullback-Leibler divergence of two outcome probability distributions based on B and {\boldsymbol{B}'} :
PL=\sum\nolimits_{l_{k} \in L}\mathrm{Pr}(\mathcal{M}({\boldsymbol{B}})=l_{k})\mathrm{ln}(\dfrac{\mathrm{Pr}(\mathcal{M}({\boldsymbol{B}})=l_{k})}{\mathrm{Pr}(\mathcal{M}({\boldsymbol{B}'})=l_{k})}), where L is the set of all the possible feasible paths for the transaction request. The smaller the PL is, the harder it is to distinguish the two bid profiles, and the better the privacy preserving of the transaction cost is.
All the simulations are run on a Windows machine with Intel Core i5-8600K CPU and 16-GB memory. Each measurement is averaged over 100 instances.
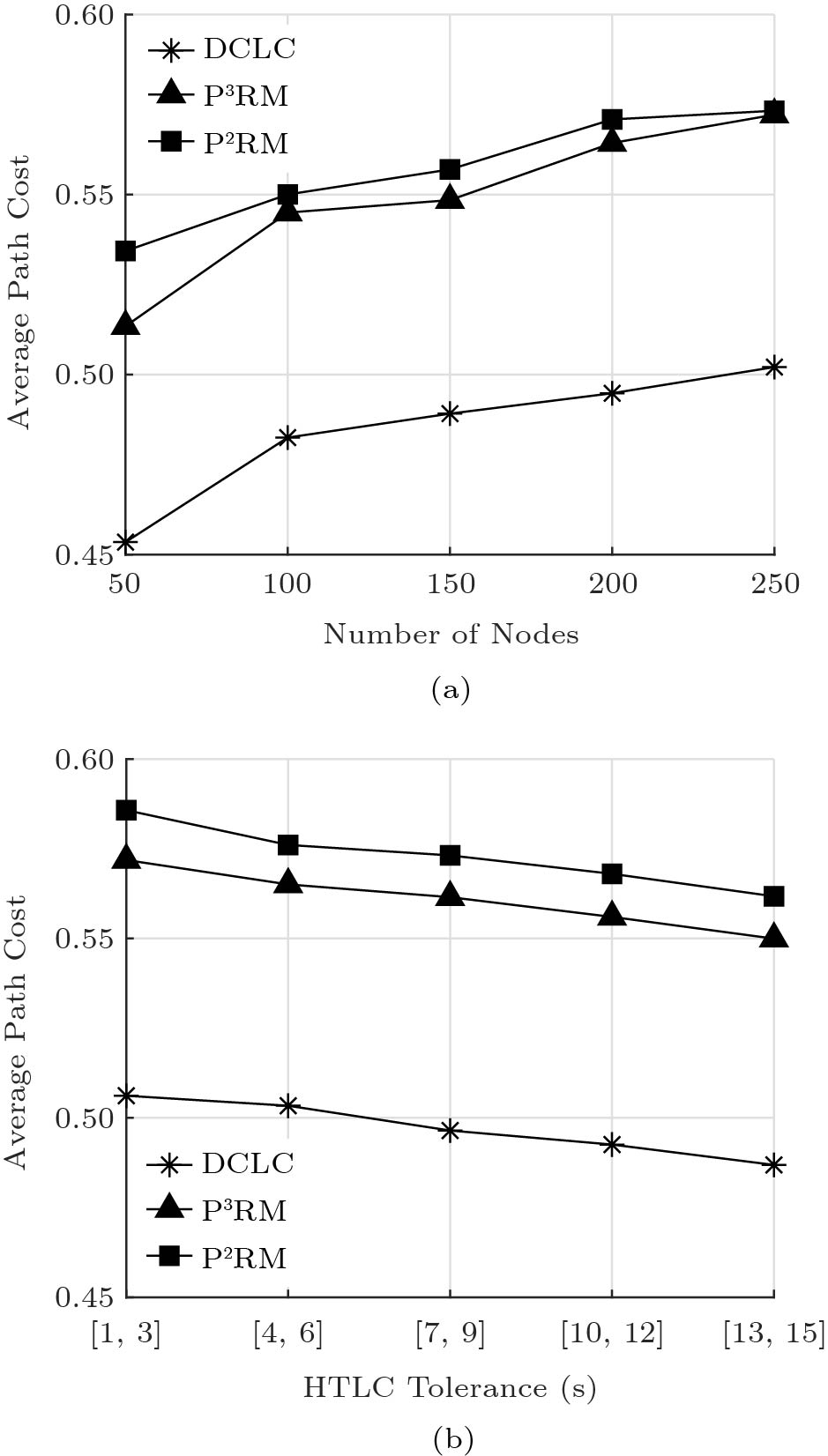
5.3 Average Path Cost
The objective of the COR problem is to minimize the path cost. We can see from Fig.6 that DCLC always has the lowest path cost, while P ^2 RM has the highest path cost. This is because DCLC has no privacy cost. P ^2 RM has the highest privacy cost since P ^2 RM has the highest privacy budget. On average, the path cost of P ^3 RM is 95% of that in P ^2 RM and 113.2% of that in DCLC. Moreover, the privacy-preserving routing mechanisms always output higher path cost than that of DCLC. This is because the privacy-preserving routing mechanisms rely on the probability to choose the shortest path, resulting in the final path they choose is not necessarily the true shortest path. We can see from Fig.6(a), the average path cost of all the three algorithms increase with the number of nodes. This is because more transactions can be completed through the paths with larger average transaction cost when the number of nodes increases. When the number of nodes increases, the maximum privacy budget of the path in P ^3 RM approaches that in P ^2 RM, and the noise in two algorithms follows the similiar pdf. Therefore, the result of path comparison in P ^3 RM is similiar to that in P ^2 RM. This indicates that the average path cost of P ^3 RM approaches that of P ^2 RM. As shown in Fig.6(b), the average path cost of all the three algorithms decrease with the increasing HTLC tolerance. This is because the increase of HTLC tolerance indicates that the sender has more chance to select the cheapest path to transfer the payment.
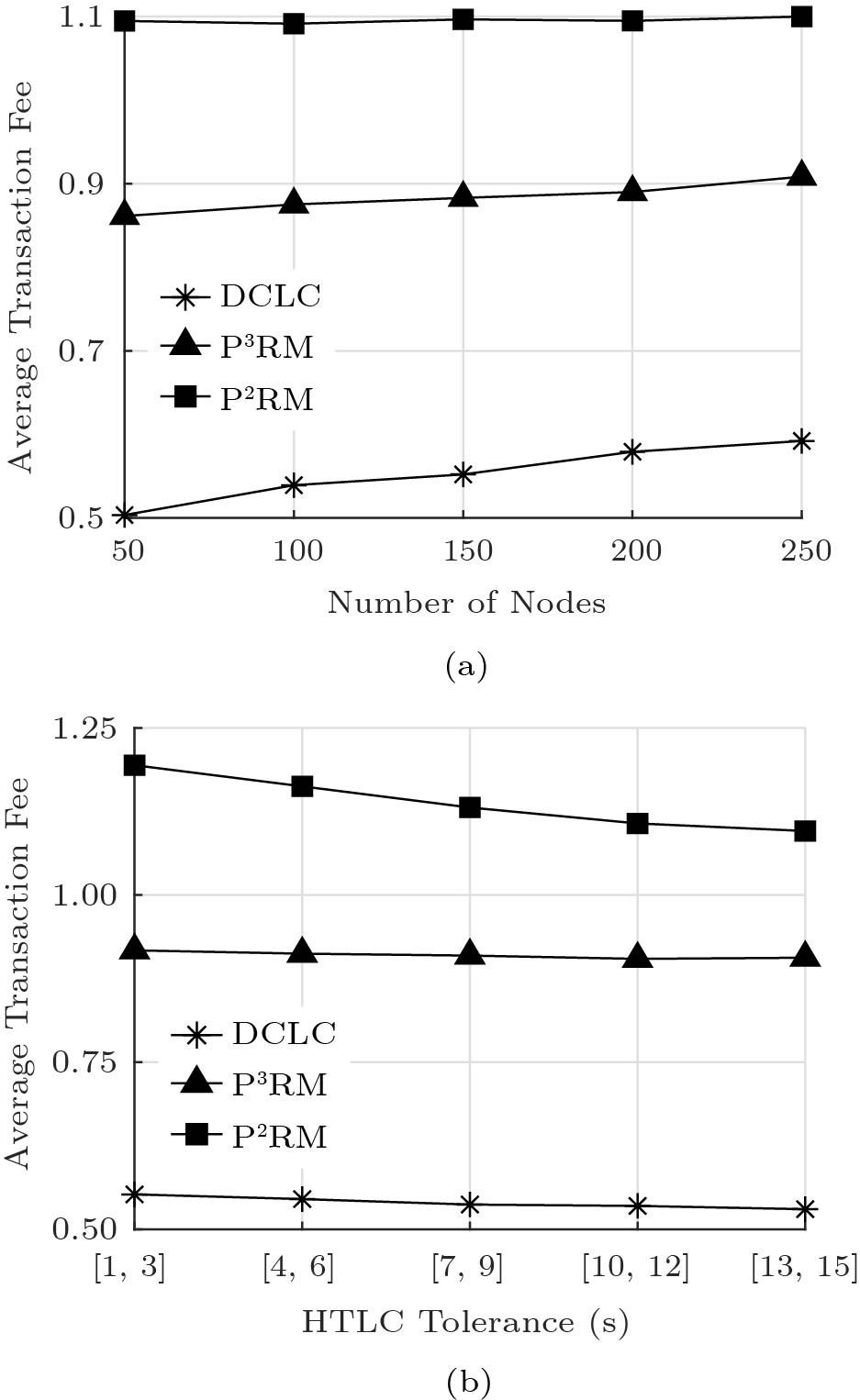
5.4 Average Transaction Fee
Fig.7 shows the average transaction fee of the final path, which is the sum of the transaction fee of each user in the final path. We can see from Fig.7(a) that the average transaction fee of the final path increases when the number of nodes increases. A larger PCN leads to a longer transaction path, and the number of winners of the path increases accordingly. As a result, the average transaction fee increases. As shown in Fig.7(b), the average transaction fee of all the three algorithms decreases with the increasing HTLC tolerance. This is because the sender can select the cheapest path when the HTLC tolerance increases, and thus, the transaction fee will decrease. P ^2 RM has the higher privacy budget, then the average path cost is higher. Thus, the average transaction fee of P ^2 RM is the highest among the three algorithms.
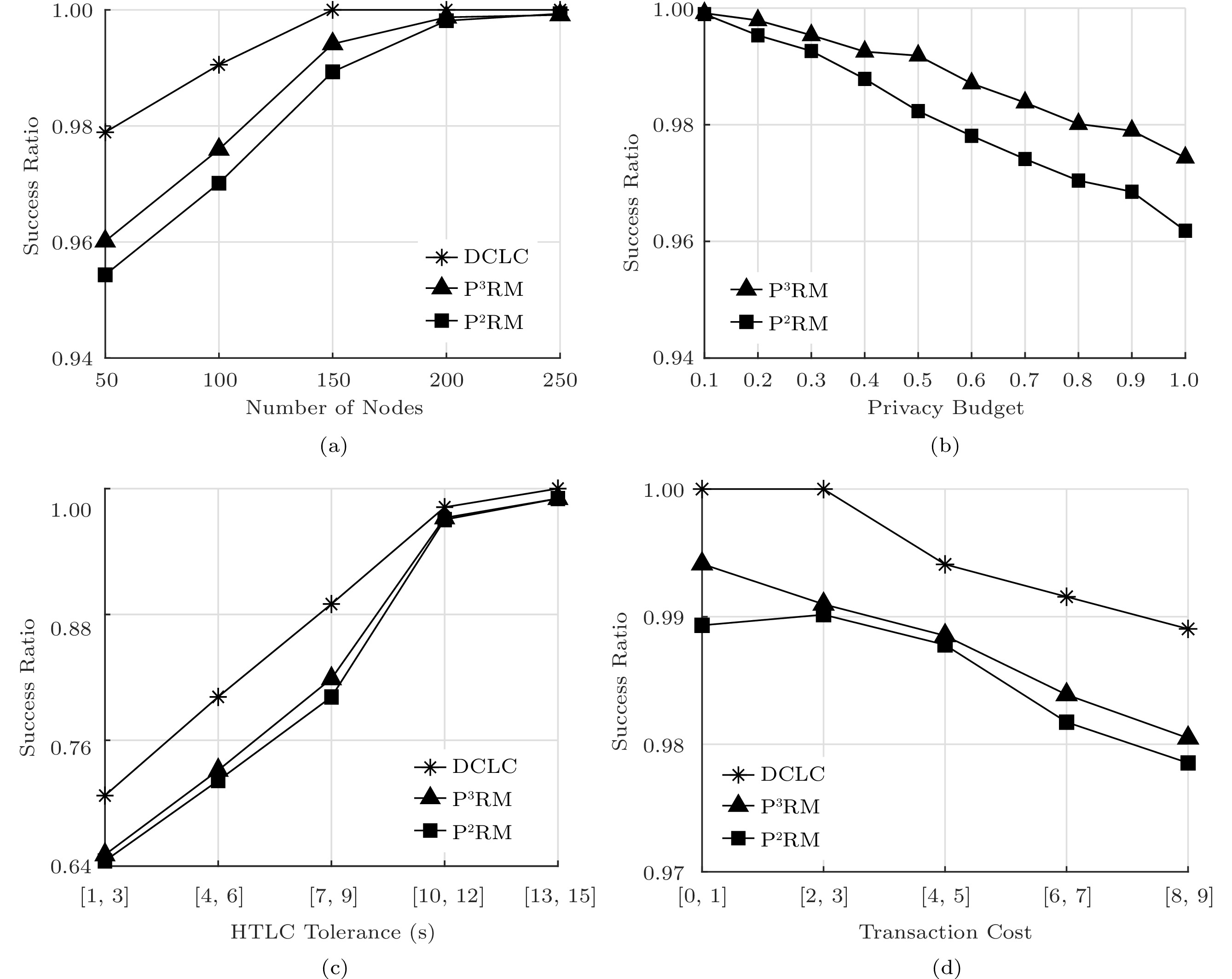
5.5 Success Ratio
Fig.8 shows the success ratio of the three algorithms. The success ratio of DCLC is the highest, and P ^2 RM is the lowest. This is because DCLC has no privacy cost, and P ^2 RM has the largest privacy budget and the largest privacy cost of each user. Therefore, under the same setting of the channel capacity, P ^2 RM has a higher probability of transaction failure. From Fig.8(a), we can see that the success ratio increases when the number of nodes increases. This is because there are more feasible paths to fulfill the transaction requests. Next, we explore the impact of privacy budget on success ratio. Note that the privacy budget of P ^3 RM is uniformly distributed over 10 ranges: [0,\;0.1],\;[0.1,\;0.2],\;\ldots ,\;[0.9,\;1] in this simulation. As shown in Fig.8(b), the success ratio decreases with the increasing privacy budget. The higher privacy budget is, the higher privacy cost is. Thus, the total path cost becomes larger, which probably causes the failure of transaction. It can be seen from Fig.8(c) that the success ratio will increase when we relax the HTLC tolerance constraint since the users have more time to transfer the payment. As shown in Fig.8(d), when the transaction cost of each user increases, the path cost increases. Thus, the success ratio decreases accordingly. Our P ^3 RM achieve 98.7% success ratio of that in DCLC averagely.
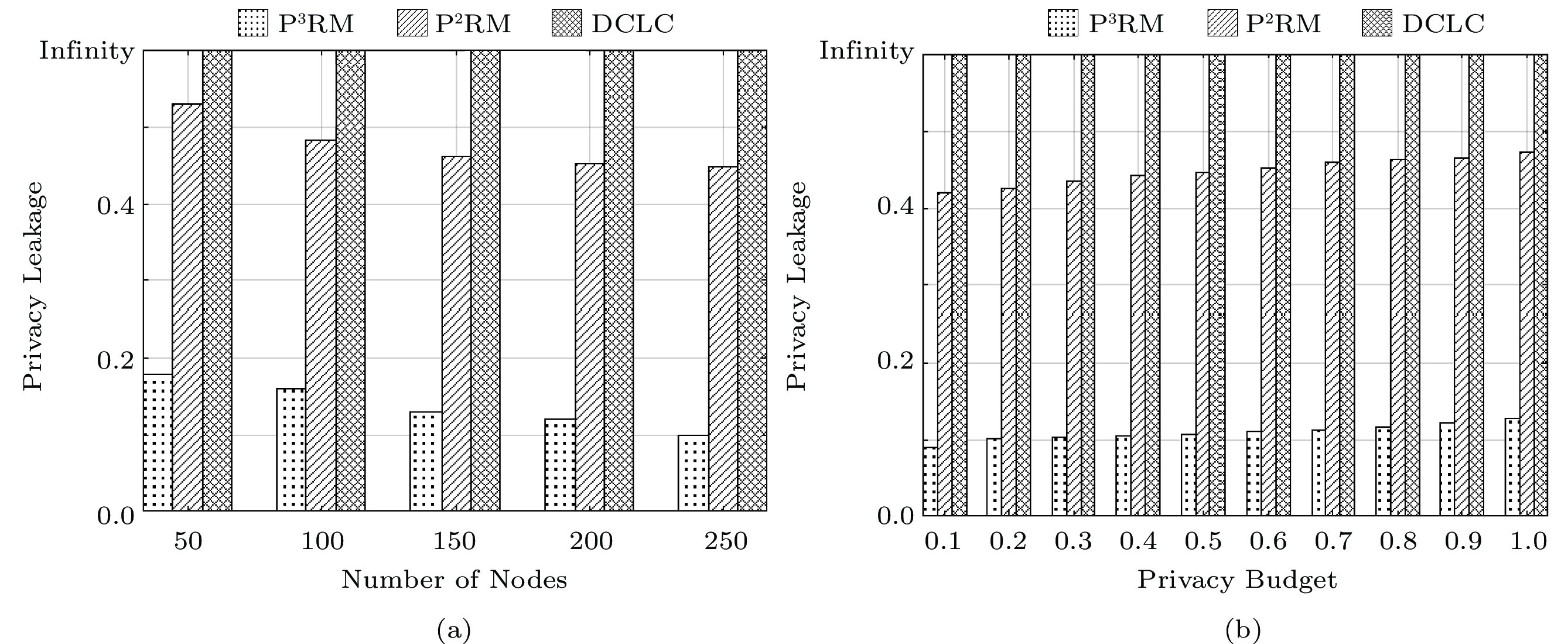
5.6 Privacy Leakage
Fig.9 shows the privacy leakage of the three algorithms. Since DCLC does not provide the privacy protection, the privacy leakage of DCLC is infinite. As shown in Fig.9(a), the PL of P ^2 RM is higher than that of P ^3 RM because the privacy budget of P ^2 RM is higher than that of P ^3 RM. The privacy leakage of P ^3 RM is lower than 0.2 since the privacy budget of P ^3 RM is uniformly distributed over [0, 1] . We can see from Fig.9(a) that P ^3 RM shows great superiority in terms of privacy protection. As shown in Fig.9(b), the privacy leakage increases with the increasing privacy budget. This is because the larger the privacy budget is, the weaker the privacy protection level can be offered by P ^3 RM and P ^2 RM according to Lemma 4.
5.7 Running Time
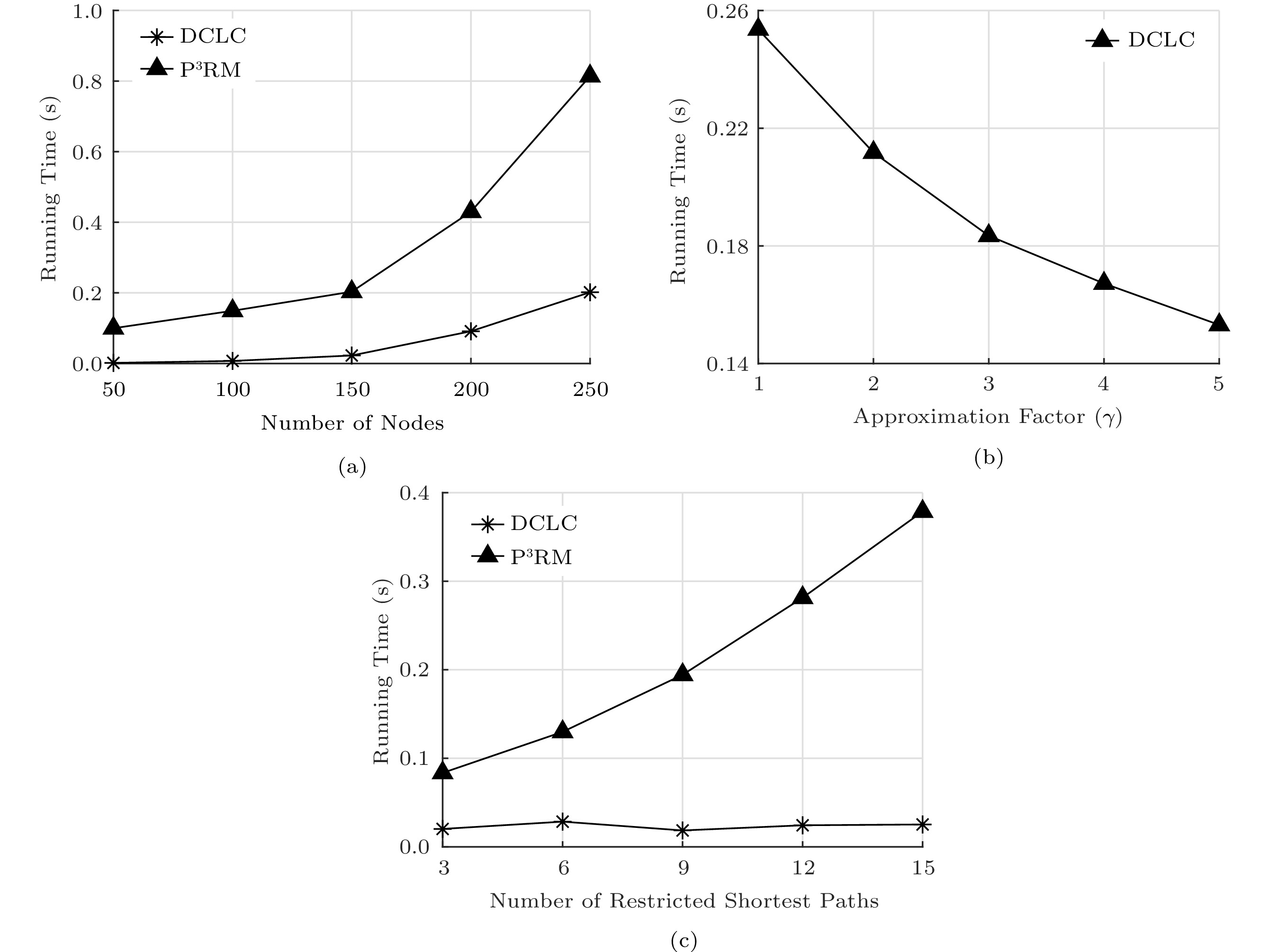
Since P ^2 RM follows the same process of P ^3 RM, we only measure the running time of P ^3 RM and DCLC. As shown in Fig.10(a), the running time of P ^3 RM and DCLC increases with the increasing number of nodes. DCLC does not consider the privacy-preserving, and the \mathcal{K} -path selection and probability comparison are not needed. Thus, the running time of DCLC is lower than that of P ^3 RM. However, our P ^3 RM can be terminated within 0.83 s for 250 nodes. Fig.10(b) shows the effect of approximation factor \gamma on running time. When \gamma increases, the upper bound of the path cost decreases, and the number of iterations of the restricted shortest path search in function DCLC decreases, thus the running time of P ^3 RM decreases accordingly. As shown in Fig.10(c), the value of \mathcal{K} affects the running time of P ^3 RM. DCLC directly selects the shortest path, and the running time of DCLC is not influenced by \mathcal{K} . Thus, the running time of DCLC keeps stable and is lower than that of P ^3 RM. With the increase of \mathcal{K} , the number of the restricted shortest paths selected by \mathcal{K} -SP increases, thus, increasing the running time of the path selection stage. Therefore, the running time of P ^3 RM increases with the increasing \mathcal{K} .
6. Conclusions
In this paper, we presented an auction-based system model for PCN using the Laplace differential privacy mechanism. We formulized the cost optimization routing problem to minimize the path cost under the constraints of the HTLC tolerance and the channel capacity. We proposed an approximation algorithm to find the top \mathcal{K} -restricted shortest paths, and designed the probability comparison function to find the final path with the highest probability of having the lowest path cost. Moreover, we applied the binary search to calculate the transaction fee of the users. Through theoretical analysis, we demonstrated that the proposed routing mechanism satisfies the desirable properties of 1/2-truthfulness, 1/4-individual rationality, and differential privacy. The experiments on the real-world datasets demonstrated that the privacy leakage of P ^3 RM is 73.21% lower than that of P ^2 RM with only 13.2% more path cost compared with DCLC on average.
-
Table 1 Frequently Used Notations
Notation Description n Number of users m Number of channels s Sender of the transaction request d Recipient of the transaction request g Payment of the transaction request W Set of users in PCN w_{i} User w_{i} {\boldsymbol{B}} Bid profile B_{i} Bid of the user w_{i} b_{ij}^{t} Bidding transaction cost of channel < lt; $$ i,\; j $> gt; $b_{l}^{t} Bidding transaction cost of path l \overline{b_{ij}^{t}} Obfuscated bidding transaction cost of channel < lt; $$ i,\; j $> gt; $\overline{b_{l}^{t}} Obfuscated bidding transaction cost of path l r_{ij} Channel capacity of channel < lt; $$ i,\; j $> gt; $t_{ij} Transaction time of channel < lt; $$ i,\; j $> gt; $\epsilon_{ij} Privacy budget of channel < lt; $$ i,\; j $> gt; $\sigma_{ij} HTLC tolerance of channel < lt; $$ i,\; j $> gt; $\eta_{ij} Laplace noise of channel < lt; $$ i,\; j $> gt; $b_{l} Bidding path cost of path l c_{i} Cost of user w_{i} c_{ij}^{t} Transaction cost of channel < lt; $$ i,\; j $> gt; $,c_{ij}^{p} Privacy cost of channel < lt; $$ i,\; j $> gt; $C_{\rm{max}} Maximum cost of a channel {{p}} Transaction fee profile p_{i} Transaction fee of user w_{i} L_{\mathcal{K}} Set of the top \mathcal{K} -restricted shortest paths \overline{b_{\mathcal{K}}} Set of the obfuscated bidding path cost of the top \mathcal{K} -restricted shortest paths S_{\mathcal{K}} Winner set of the top \mathcal{K} -restricted shortest paths l_{k} The k -th path in top \mathcal{K} -restricted shortest paths l_{k}^{v} Deviating path of the v -th user on the k -th path S_{k}^{v} Winner set of the deviating path of the v -th user on the k -th path \overline{b_{l_{k}}^{v}} Obfuscated bidding path cost of the deviating path of the v -th user on the k -th path w_{v}^{k} The v -th deviating user of the k -th path \overline{b_{l_{k}}} Obfuscated bidding path cost of the k -th path S_{k} Winner set of the k -th path l_{0} Path before the deviating user l_{f} Final path S_{f} Winner set of the final path p_{l_{f}} Transaction fee profile of winners in the final path l_{f} \alpha Coefficient to scale the value of privacy cost \gamma Approximation factor \delta Search precision Table 2 Parameter Settings
Parameter Value n 150 c_{ij}^{t} Uniform distribution over (0, 1] \alpha 0.5 \epsilon_{ij} Uniform distribution over (0, 1] \sigma_{ij} Uniform distribution over [13, 15] t_{ij} Uniform distribution over [0.5,1] g [10,1\;000] C_{\mathrm{max}} 10 \mathcal{K} 9 \gamma 2 \delta 0.02 -
[1] Nakamoto S. Bitcoin: A peer-to-peer electronic cash system. Bitcoin, 2008.
[2] Buterin V. A next-generation smart contract and decentralized application platform. Etherum, 2014.
[3] Xu J, Wu Y, Luo X, Yang D. Improving the efficiency of blockchain applications with smart contract based cyber-insurance. In Proc. the 2020 IEEE International Conference on Communications (ICC), Jun. 2020. DOI: 10.1109/ICC40277.2020.9149301.
[4] Decker C, Wattenhofer R. A fast and scalable payment network with bitcoin duplex micropayment channels. In Proc. the 17th International Symposium on Stabilization, Safety, and Security of Distributed Systems, Aug. 2015, pp.3–18. DOI: 10.1007/978-3-319-21741-3_1.
[5] Zhang Y, Yang D, Xue G. CheaPay: An optimal algorithm for fee minimization in blockchain-based payment channel networks. In Proc. the 2019 IEEE International Conference on Communications (ICC), May. 2019. DOI: 10.1109/ICC.2019.8761804.
[6] Di Stasi G, Avallone S, Canonico R, Ventre G. Routing payments on the lightning network. In Proc. the 2018 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Jul. 30–Aug. 3, 2018, pp.1161–1170. DOI: 10.1109/Cybermatics_2018.2018.00209.
[7] Yu R, Xue G, Kilari V T, Yang D, Tang J. CoinExpress: A fast payment routing mechanism in blockchain-based payment channel networks. In Proc. the 27th International Conference on Computer Communication and Networks (ICCCN), Jul. 30–Aug. 2, 2018. DOI: 10.1109/ICCCN.2018.8487351.
[8] Wang Z, Li J, Hu J, Ren J, Li Z, Li Y. Towards privacy-preserving incentive for mobile crowdsensing under an untrusted platform. In Proc. the 2019 IEEE Conference on Computer Communications, Apr. 29–May 2, 2019, pp.2053–2061. DOI: 10.1109/INFOCOM.2019.8737594.
[9] Xu J, Luo Z, Guan C, Yang D, Liu L, Zhang Y. Hiring a team from social network: Incentive mechanism design for two-tiered social mobile crowdsourcing. IEEE Trans. Mobile Computing, 2023, 22(8): 4664–4681. DOI: 10.1109/TMC.2022.3162108.
[10] Xu J, Rao Z, Xu L, Yang D, Li T. Incentive mechanism for multiple cooperative tasks with compatible users in mobile crowd sensing via online communities. IEEE Trans. Mobile Computing, 2020, 19(7): 1618–1633. DOI: 10.1109/TMC.2019.2911512.
[11] Lu W, Zhang S, Xu J, Yang D, Xu L. Truthful multi-resource transaction mechanism for P2P task offloading based on edge computing. IEEE Trans. Vehicular Technology, 2021, 70(6): 6122–6135. DOI: 10.1109/TVT.2021.3079258.
[12] Zhang D, Tan L, Ren J, Awad M, Zhang S, Zhang Y, Wan P. Near-optimal and truthful online auction for computation offloading in green edge-computing systems. IEEE Trans. Mobile Computing, 2020, 19(4): 880–893. DOI: 10.1109/TMC.2019.2901474.
[13] Cheng K, Wang L, Shen Y, Liu Y, Wang Y, Zheng L. A lightweight auction framework for spectrum allocation with strong security guarantees. In Proc. the 2020 IEEE Conference on Computer Communications, Jul. 2020, pp.1708–1717. DOI: 10.1109/INFOCOM41043.2020.9155279.
[14] Xue G, Xu J, Wu H, Lu W, Xu L. Incentive mechanism for rational miners in Bitcoin mining pool. Information Systems Frontiers, 2021, 23(2): 317–327. DOI: 10.1007/s10796-020-10019-2.
[15] Wang Y, Wang W, Dahlberg T A. Truthful routing for wireless hybrid networks. In Proc. the 2005 IEEE Global Telecommunications Conference, Nov. 28–Dec. 2, 2005, pp.3460–3465. DOI: 10.1109/GLOCOM.2005.1578416.
[16] McSherry F, Talwar K. Mechanism design via differential privacy. In Proc. the 48th Annual IEEE Symposium on Foundations of Computer Science, Oct. 2007, pp.94–103. DOI: 10.1109/FOCS.2007.66.
[17] Dwork C. Differential privacy: A survey of results. In Proc. the 5th International Conference on Theory and Applications of Models of Computation, Apr. 2008. DOI: 10.1007/978-3-540-79228-4_1.
[18] Wallace K A. Anonymity. Ethics and Information Technology, 1999, 1(1): 21–31. DOI: 10.1023/A:1010066509278.
[19] Alenezi M N, Alabdulrazzaq H K, Mohammad N Q. Symmetric encryption algorithms: Review and evaluation study. International Journal of Communication Networks and Information Security, 2022, 12(2): 256–272. DOI: 10.17762/ijcnis.v12i2.4698.
[20] Wang Z, Hu J, Lv R, Wei J, Wang Q, Yang D, Qi H. Personalized privacy-preserving task allocation for mobile crowdsensing. IEEE Trans. Mobile Computing, 2019, 18(6): 1330–1341. DOI: 10.1109/TMC.2018.2861393.
[21] Zhang X, Shi S, Qian C. Scalable decentralized routing for blockchain payment networks. In Proc. the 3rd International Symposium on Foundations and Applications of Blockchain, May 2020.
[22] Khalil R, Gervais A. Revive: Rebalancing off-blockchain payment networks. In Proc. the 2017 ACM SIGSAC Conference on Computer and Communications Security, Oct. 2017, pp.439–453. DOI: 10.1145/3133956.3134033.
[23] Zhang Y, Yang D. RobustPay: Robust payment routing protocol in blockchain-based payment channel networks. In Proc. the 27th International Conference on Network Protocols (ICNP), Oct. 2019. DOI: 10.1109/ICNP.2019.8888094.
[24] Tripathy S, Mohanty S K. MAPPCN: Multi-hop anonymous and privacy-preserving payment channel network. In Proc. the 2020 International Conference on Financial Cryptography and Data Security, Feb. 2020, pp.481–495. DOI: 10.1007/978-3-030-54455-3_34.
[25] Mazumdar S, Ruj S. CryptoMaze: Privacy-preserving splitting of off-chain payments. IEEE Trans. Dependable and Secure Computing, 2023, 20(2): 1060–1073. DOI: 10.1109/TDSC.2022.3148476.
[26] Yu B, Kermanshahi S K, Sakzad A, Nepal S. Chameleon hash time-lock contract for privacy preserving payment channel networks. In Proc. the 13th International Conference on Provable Security, Oct. 2019, pp.303–318. DOI: 10.1007/978-3-030-31919-9_18.
[27] Herrera-Joancomarti J, Navarro-Arribas G, Ranchal-Pedrosa A, Perez-Sola C, Garcia-Alfaro J. On the difficulty of hiding the balance of lightning network channels. In Proc. the 2019 ACM Asia Conference on Computer and Communications Security, Jul. 2019, pp.602–612. DOI: 10.1145/3321705.3329812.
[28] Tang W, Wang W, Fanti G, Oh S. Privacy-utility tradeoffs in routing cryptocurrency over payment channel networks. In Proc. the 2020 ACM on Measurement and Analysis of Computing Systems, Jun. 2020, Article No. 29. DOI: 10.1145/3392147.
[29] Roos S, Moreno-Sanchez P, Kate A, Goldberg I. Settling payments fast and private: Efficient decentralized routing for path-based transactions. In Proc. the 25th Annual Network and Distributed System Security Symposium, Feb. 2018, pp.455–471. DOI: 10.48550/arXiv.1709.05748.
[30] Li P, Luo X F, Miyazaki T, Guo S. Privacy-preserving payment channel networks using trusted execution environment. In Proc. the 2020 IEEE International Conference on Communications (ICC), Jun. 2020. DOI: 10.1109/ICC40277.2020.9149447.
[31] Niu B, Chen Y, Wang B, Cao J, Li F. Utility-aware exponential mechanism for personalized differential privacy. In Proc. the 2020 IEEE Wireless Communications and Networking Conference (WCNC), May 2020. DOI: 10.1109/WCNC45663.2020.9120532.
[32] Jorgensen Z, Yu T, Cormode G. Conservative or liberal? Personalized differential privacy. In Proc. the 31st International Conference on Data Engineering, Apr. 2015, pp.1023–1034. DOI: 10.1109/ICDE.2015.7113353.
[33] Duchi J C, Jordan M I, Wainwright M J. Local privacy and statistical minimax rates. In Proc. the 54th Annual Symposium on Foundations of Computer Science, Oct. 2013, pp.429–438. DOI: 10.1109/FOCS.2013.53.
[34] Jin X, Zhang Y. Privacy-preserving crowdsourced spectrum sensing. IEEE/ACM Trans. Networking, 2018, 26(3): 1236–1249. DOI: 10.1109/TNET.2018.2823272.
[35] Lin J, Yang D, Li M, Xu J, Xue G. Frameworks for privacy-preserving mobile crowdsensing incentive mechanisms. IEEE Trans. Mobile Computing, 2018, 17(8): 1851–1864. DOI: 10.1109/TMC.2017.2780091.
[36] Lv D, Zhu S. Achieving correlated differential privacy of big data publication. Computers & Security, 2019, 82: 184–195. DOI: 10.1016/j.cose.2018.12.017.
[37] Wang T, Mei Y, Jia W, Zheng X, Wang G, Xie M. Edge-based differential privacy computing for sensor-cloud systems. Journal of Parallel and Distributed Computing, 2020, 136: 75–85. DOI: 10.1016/j.jpdc.2019.10.009.
[38] Wei K, Li J, Ding M, Ma C, Yang H H, Farokhi F, Jin S, Quek T Q S, Poor H V. Federated learning with differential privacy: Algorithms and performance analysis. IEEE Trans. Information Forensics and Security, 2020, 15: 3454–3469. DOI: 10.1109/TIFS.2020.2988575.
[39] Bao T, Xu L, Zhu L, Wang L, Li T. Successive point-of-interest recommendation with personalized local differential privacy. IEEE Trans. Vehicular Technology, 2021, 70(10): 10477–10488. DOI: 10.1109/TVT.2021.3108463.
[40] Dwork C, Roth A. The algorithmic foundations of differential privacy. Foundations and Trends® in Theoretical Computer Science, 2014, 9(3/4): 211–407. DOI: 10.1561/0400000042.
[41] McSherry F D. Privacy integrated queries: An extensible platform for privacy-preserving data analysis. In Proc. the 2009 ACM SIGMOD International Conference on Management of Data, Jun. 2009, pp.19–30. DOI: 10.1145/1559845.1559850.
[42] Hassin R. Approximation schemes for the restricted shortest path problem. Mathematics of Operations Research, 1992, 17(1): 36–42. DOI: 10.1287/moor.17.1.36.
[43] Yen J Y. Finding the K shortest loopless paths in a network. Management Science, 1971, 17(11): 712–716. DOI: 10.1287/mnsc.17.11.712.
[44] Xue G, Zhang W, Tang J, Thulasiraman K. Polynomial time approximation algorithms for multi-constrained QoS routing. IEEE/ACM Trans. Networking, 2008, 16(3): 656–669. DOI: 10.1109/TNET.2007.900712.
[45] Singla A, Krause A. Truthful incentives in crowdsourcing tasks using regret minimization mechanisms. In Proc. the 22nd International Conference on World Wide Web, May 2013, pp.1167–1178. DOI: 10.1145/2488388.2488490.
-
其他相关附件
-
本文附件外链
https://rdcu.be/d6X8I -
DOCX格式
2635-Chinese Information 点击下载(34KB) -
PDF格式
2024-6-11-2635-Highlights 点击下载(178KB)
-




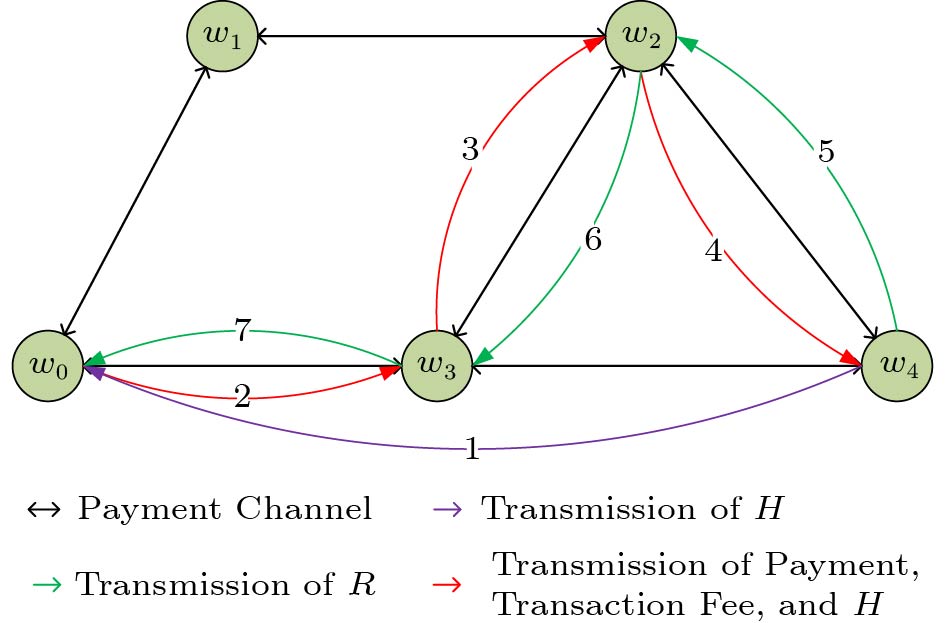
 下载:
下载: