1.   Introduction

Human brain can perform various cognitive tasks in an unmatched efficiency with the capacity of about one liter and power of 20 watts^[1]. An important reason for the high efficiency of the brain lies in the event-based computation. The spiking neural network (SNN) is a representative event-based learning algorithm inspired by the human brain^[2-4]. The information in SNNs is transmitted through sparse and asynchronous spikes, and the computation is performed locally and in distributed neurons and synapses in parallel^[5]. Nowadays, various neuromorphic devices such as TrueNorth^[5] and Loihi^[6], have been proposed to accelerate SNNs with compatible computing units and architectures. With abundant hardware resources of neuromorphic devices, we can implement high-performance intelligent systems given an effective SNN algorithm^{[7, 8]}.

Event-based sensors, such as dynamic vision sensors (DVS), have also attracted considerable attention recently^{[9, 10]}. Unlike traditional frame-based vision sensors, DVS can generate event-based visual information by recording the pixel-level intensity change in a microsecond^[11]. Besides, DVS has a much higher dynamic range and output rate than frame-based vision sensors^[12]. More importantly, the event-based information representation of DVS can release the downstream algorithms from processing abundant information, offering significant speed and efficiency advantages^[13].

Amir et al.^[9] proposed an end-to-end event-based gesture recognition system by combining SNN and DVS. However, the fascinating accuracy relies on a large-scale network complexity of more than 200000 neurons. The computing resources on the TrueNorth processor, with 1 million neurons and 256 million synapses, nearly run out when performing the recognition task. In essence, the expensive training cost of [9] is induced by the backpropagation-based training method and the architecture of the deep convolutional neural network (CNN). Another two studies^{[13, 14]}, using the same approach of SNN with the CNN architecture, also achieved similar accuracies while facing the same challenge of large network complexity and expensive training cost.

To address the above challenges, we adopt a liquid state machine (LSM) based method for event-based vision tasks. An LSM is mainly composed of a liquid of spiking neurons and a simple classifier, such as perceptron. The spiking neurons in the liquid are connected randomly, which can project input spike trains to linearly-separable spiking patterns of neurons in the liquid, referred to as a liquid state (LS)^{[15, 16]}. Then, the liquid state is sent to the classifier as input for training or inference. Typically, the liquid state for classification is the spike number of liquid neurons counted at the end of the presentation of one input sample. And the weights of synapse connections are randomly assigned and fixed during the training and test procedures^{[15, 17]}. The training cost in an LSM is only induced by the simple classifier. In a traditional LSM, there is only one liquid of neurons, and all synapse weights are randomly assigned^{[15, 17]}. Since STDP (spike-timing dependent plasticity) can enhance synapse connection with causal relationships and weaken the synapse connection without causal relationships, some work has adopted STDP for training the LSM to get better performance^{[18, 19]}. With a simplistic structure and low training cost, LSMs could outperform other artificial neural networks in terms of energy and speed^{[13, 18]}. Kaiser et al.^[17] successfully applied an LSM to predict the event stream generated by DVS. However, no work has been reported to apply LSMs for the application of event-based vision recognition.

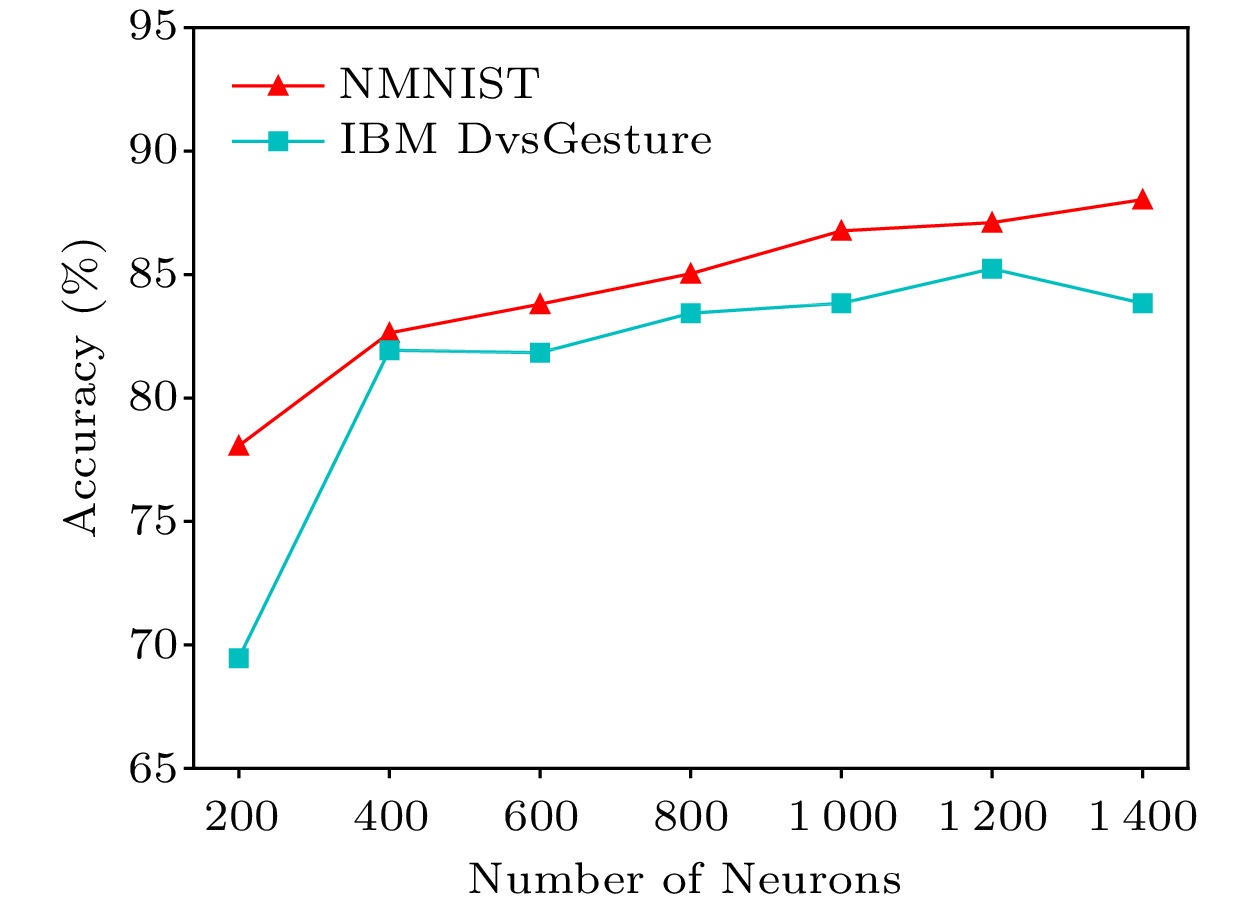
In this work, we first evaluate the performance of the traditional LSM model. We also adopt the STDP rule to tune the randomly-assigned synapse weights. We use two DVS datasets, NMNIST^[20] and IBM DvsGesture^[9], for performance evaluation. By increasing the neuron number, the classification accuracy was only 87% and 83% on NMNIST and IBM DvsGesture, respectively. The state-of-the-art accuracy of other event-based algorithms is 98%^{[13, 14]} and 94%^[9] on NMNIST and IBM DvsGesture, respectively. Despite the low power and small complexity, the existing LSM cannot be applied for event-based vision recognition due to the low accuracy. Therefore, focusing on classification accuracy, we propose the following two methods to improve the performance of LSM.

● Since the spatiotemporal features of the input may vary over time, we propose multi-state fusion (MSF) that samples the spike number of liquid neurons at more than one timestep which can reserve more spatiotemporal features.

● Furthermore, we create a network architecture search (NAS) framework to explore the architecture potential of LSMs with multiple liquids. Specifically, many liquids are arranged in the hierarchical multi-layer structure. Liquids in one layer are not connected, while liquids in different layers are connected forward.

The LSM, improved by the above two methods, is named as M-LSM in this paper. Finally, M-LSM achieves classification accuracies of 97% and 92% on NMNIST and IBM DvsGesture, respectively, which are comparable to state-of-the-art accuracies with less training cost than existing approaches of SNNs.

2.   Preliminaries

This section introduces the model of traditional LSM and STDP learning rules.

2.1   LSM Model

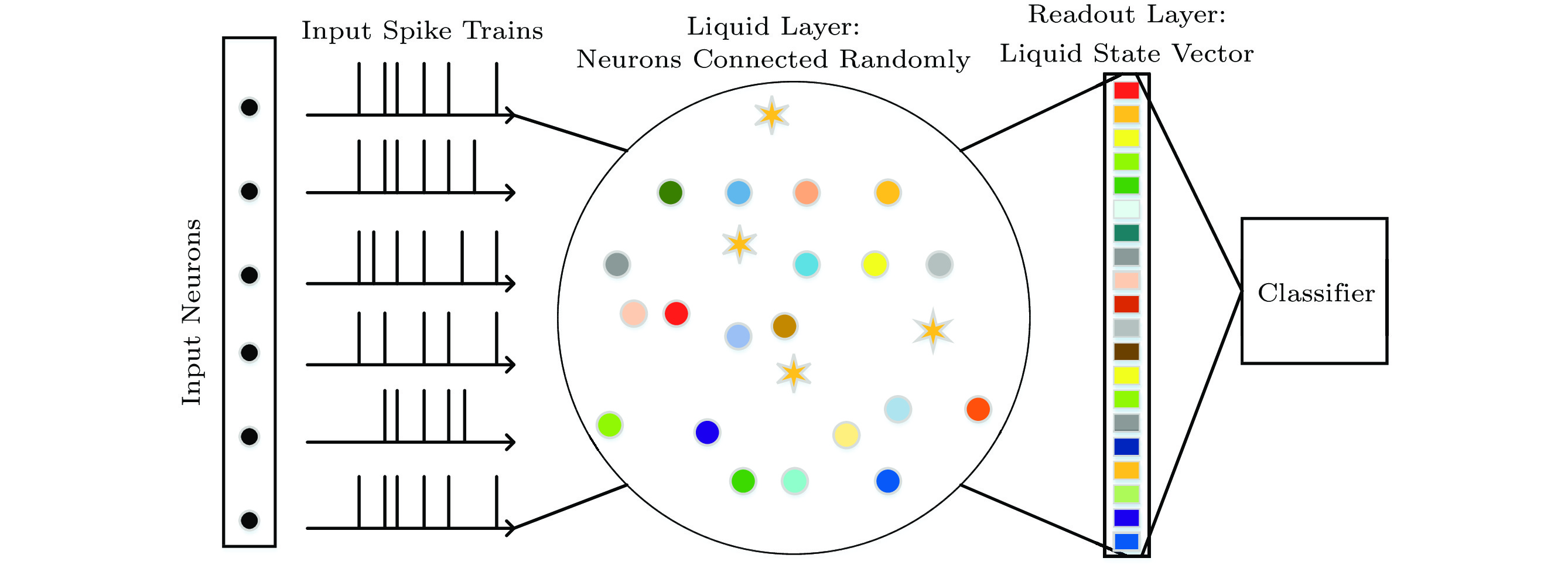
The network structure of the basic LSM model is shown in Fig.1. The computing function of an LSM is implemented by a liquid of spiking neurons with recurrent connections. There are two kinds of neurons, including excitatory and inhibitory neurons. The spike from excitatory neurons could increase the membrane potential of the post-synaptic neuron while the spike from inhibitory neurons could decrease the membrane potential of the post-synaptic neuron. The neuron will fire a spike if the membrane potential exceeds the threshold, and the membrane potential will reset to the level of $E_{\rm{reset}}$ after firing. In this work, both excitatory and inhibitory neurons are modeled as leaky-integrate-and-fire (LIF) neurons with different parameters and the dynamic behavior of an LIF neuron can be described as (1)^[4]:

Figure  1.  Schematic of the basic LSM model, composed of an input layer, a liquid layer, a readout layer, and a classifier. Every input neuron is responsible for emitting the spikes of the corresponding input channel. The liquid is composed of randomly connected excitatory neurons (indicated by circles with different colors) and inhibitory neurons (indicated by orange stars). Input neurons are randomly connected to the excitatory neurons in the liquid. The liquid state vector is composed of the spike number of sampled liquid neurons after a spike train. Synapse connections are not plotted explicitly.

下载: 全尺寸图片 幻灯片

where $V$ is the variable of membrane potential, and $\tau$ is the time constant. $E_{\rm{rest}}$ is the resting membrane potential. $E_{\rm{exc}}$ and $E_{\rm{inhi}}$ are the equilibrium potentials of excitatory and inhibitory synapses, respectively. $g_{\rm e}$ and $g_{\rm i}$ are the total conductance of all connected excitatory and inhibitory synapses that are transmitting spikes, respectively.

The input layer is sparsely connected to neurons in the liquid to feed the input spike train. Stimulated by input spikes, the neurons in the liquid will, with recurrent connections, run into a corresponding echo state^[17]. In other words, the input spike train is projected to the corresponding liquid state^{[15, 16]}. After projection, a classifier is connected to classify the liquid state. For training traditional LSMs, input samples are fed into the liquid to generate the corresponding liquid states. Then, the liquid states and corresponding labels are used to train the classifier. For the test, each test example is first fed into the liquid to generate the liquid state. Then, the liquid state is sent to the classifier for classification.

Except for the neural model parameters, a liquid is mainly defined by the parameters listed in Table 1. $R$ is the ratio of excitatory neurons to all neurons. Whether to make a link from neuron $a$ to neuron $b$ is determined using a probability $C_{ab}$. For instance, $C_{\rm EI}$ means neuron $a$ is excitatory (E) and neuron $b$ is inhibitory (I). Except for the neuron number, the others are shared by all models evaluated in this work.

Table  1.  Internal Parameters of the Liquid

Parameter	Value
R	0.8
CEE	0.4
CEI	0.4
CIE	0.5
CII	0.1

下载: 导出CSV 

| 显示表格

2.2   STDP-Tuning

STDP is a local unsupervised learning mechanism that can tune the synapse weight according to the timing of pre- and post-synaptic spikes^[18]. If one post-synaptic neuron just fires after the pre-synaptic neuron during a time window, which means the pre-synaptic neuron contributes to the excitation of the post-synaptic neuron, the synapse weight will be increased to a higher value. Conversely, if the post-synaptic neuron fires before the pre-synaptic neuron, the synapse weight will be decreased to a lower value. The effect of the STDP learning is to strengthen the connection with causal relationships and to weaken the connection without causal relationships. (2) presents a model of weight modification under the STDP rule as follows:

The model was inspired by the physical dynamics of memristor, and was first proposed in [4]. $\Delta{w}$ is the change value of the synapse weight. $\alpha_{p}$, $\alpha_{d}$, $\beta_{p}$ and $\beta_{d}$ are the parameters to model the physical character of the memristor. $w$ is the weight value, and $w_{\rm{max}}$ and $w_{\rm{min}}$ are the maximum and minimum values of the weight (the conductance of the memristor), respectively. $t_{\rm{pre}}$ and $t_{\rm{post}}$ are the spike time of the pre- and post-synaptic neuron, respectively.

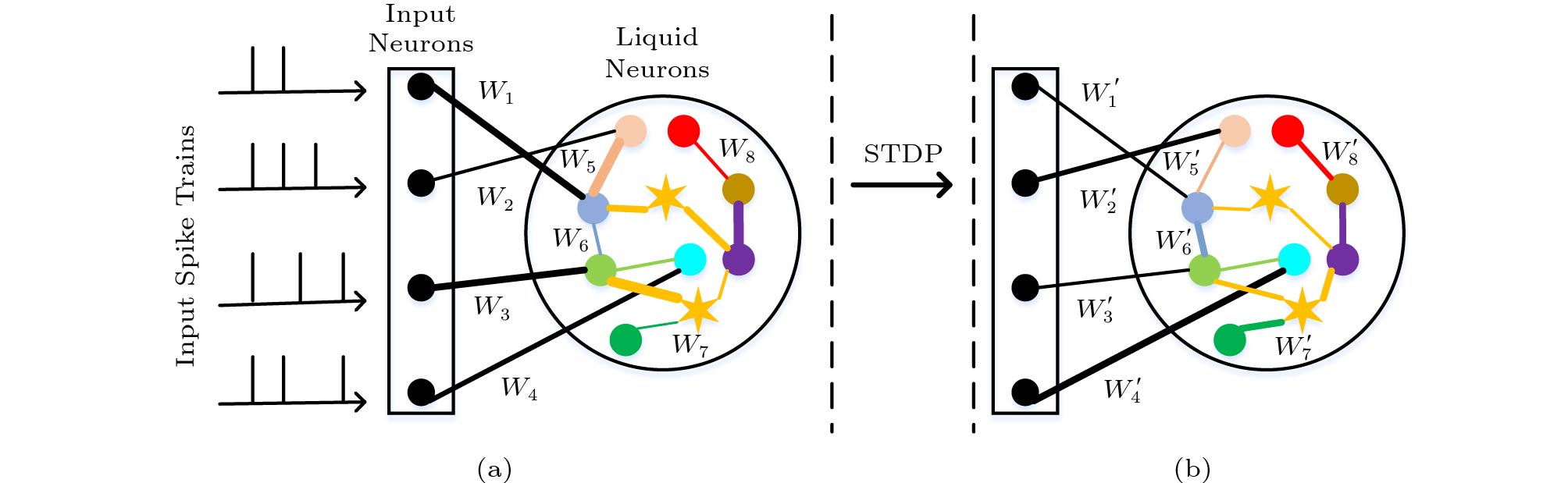
As shown in Fig.2, there are two parts in an LSM that have synapse connections. The first part is the connections between input and liquid neurons (represented by black lines). The second part is the recurrent connection among neurons in the liquid (represented by colored lines). In the traditional LSM model, the synapse weights are assigned randomly from a specific distribution, such as a normal distribution. By applying STDP on synapses, we can strengthen the connection with causal relationships and weaken the connection without causal relationships. Intuitively, STDP could improve the causal relationship between the input spike pattern and the corresponding liquid state, thus improving the separation and approximation property of the liquid. Therefore, we adopt STDP to curve the synapse weights for performance improvement. Specifically, STDP-tuning is performed before the traditional training procedure. The input spike trains from the training samples are fed to the liquid one by one. All the synapse weights are allowed to be modified by STDP. After STDP-tuning, the synapse weights are fixed during the following training and test.

Figure  2.  Mechanism of STDP-tuning. The strength of the weights is indicated by the thickness of the connections. Initially, synapse weights are assigned from a normal distribution. Then, we feed the spike trains of training samples into the liquid, allowing STDP learning on all the synapses. For example, from (a) to (b), the thickness of the connections has changed, which means that the weights have been fine-tuned, such as W₁ and W₂. After training by a number of samples, the synapse weights will be tuned to new values and fixed in the following training and test procedure.

下载: 全尺寸图片 幻灯片

3.   Methods

In this section, we propose two methods to improve the performance of LSM for the application of event-based vision recognition.

3.1   Multi-State Fusion

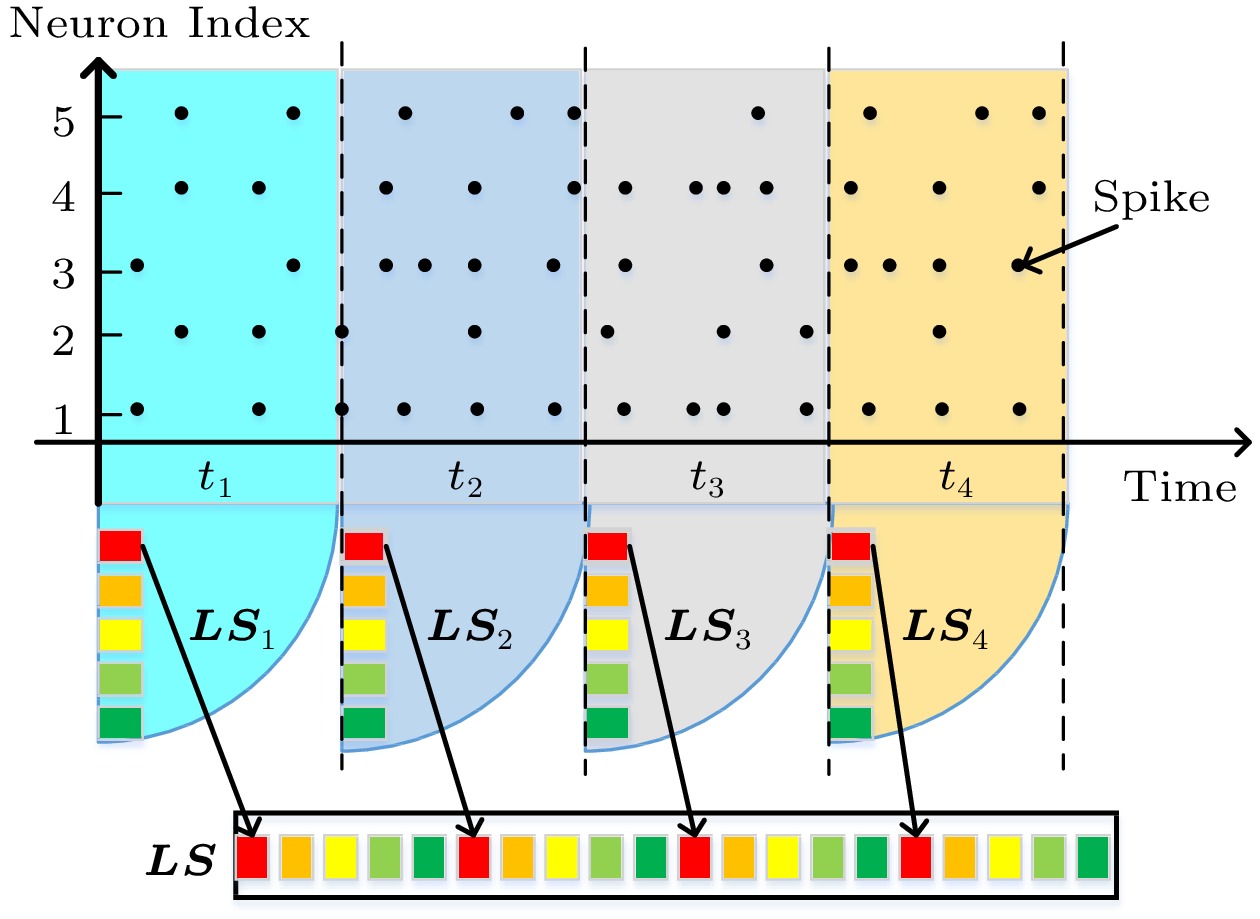
In the classical LSM, the LS for classification is the number of spikes generated by the liquid neurons at the end of one input sample. Considering that the spatiotemporal feature of the input is changing over time, sampling the liquid states several times rather than just at the end of the input may get richer temporal information. Therefore, we propose a method named multi-state fusion (MSF) to generate a more detailed liquid state for classification. As shown in Fig.3, the input stream of one example is divided into four parts evenly. Then, the spike number of the five liquid neurons at the four key timesteps is counted individually. Finally, a ($4\times5$)-length state vector is generated for classification. Obviously, the ($4\times5$)-elements state vector could provide more fine-grained spatiotemporal information than the single 5-element state vector in the traditional method.

Figure  3.  Example of MSF with five neurons in the liquid. It generates four liquid state vectors LS₁, LS₂, LS₃, and LS₄ by counting the number of spikes of the five neurons at t₁, t₂, t₃, and t₄, respectively. Then, LS₁, LS₂, LS₃, and LS₄ are concatenated to form the final LS for classification.

下载: 全尺寸图片 幻灯片

3.2   NAS for Multi-Liquid LSM

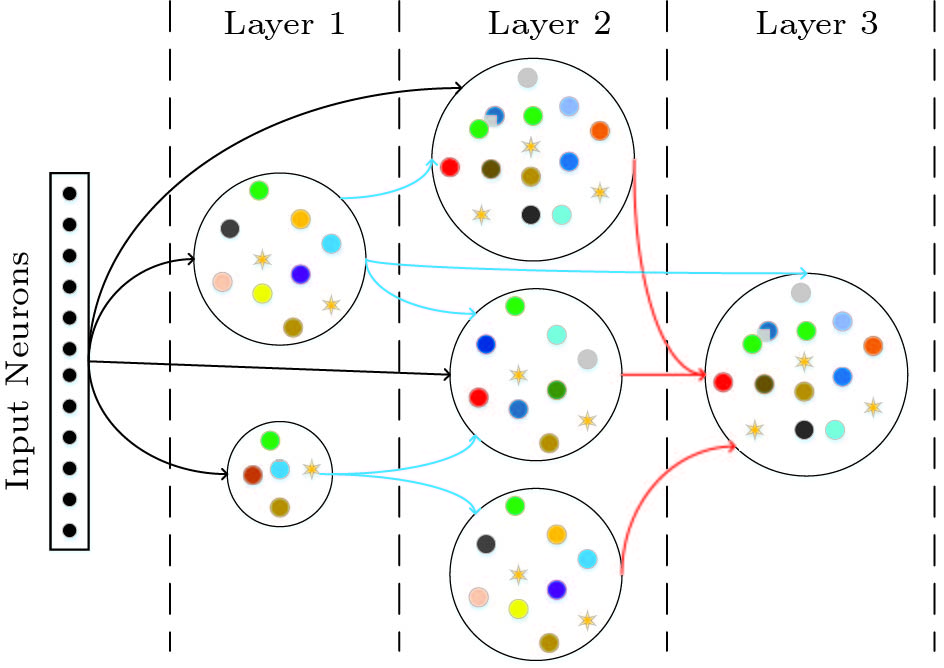
Previous work has reported performance improvement by using multiple liquids with parallel or sequential connection between liquids. However, the LSM model with both parallel and sequential connections among multiple liquids has not been studied. For further performance improvement, we propose a NAS-based framework to exploit the architecture potential of multi-liquid LSM. We define a hierarchical architecture search space of multiple layers and liquids. First, there is more than one liquid in one layer. Second, multiple liquids in one layer are not connected with each other. Third, liquids in the pre-layer and the input layer have the opportunity to connect to liquids in the post-layer. On the contrary, liquids in the post-layer have no chance to connect to the liquids in the pre-layer.

Internal parameters of a single liquid are the same as listed in Table 1, except the neuron number. Fig.4 gives an example of three-layer six-liquid architecture.

Figure  4.  Example of a three-layer six-liquid hierarchical architecture of LSM. The connections from different layers are indicated by different colors.

下载: 全尺寸图片 幻灯片

We do not aim at finding the most optimistic architecture but try to exploit the architecture potential of multi-liquid LSM. Therefore, we define a limited search space, as listed in Table 2, and only use a random search algorithm to explore the search space. The connection probability between liquids in two layers is also a hyper-parameter.

Table  2.  Parameters of the Search Space

Parameter	Value
Number of layer(s)	[1, 5]
Number of liquid(s)	[1, 10]
Number of neuron(s)	[200, 800]
Connection probability between liquids	[0.01 , 0.12]

下载: 导出CSV 

| 显示表格

4.   Experimental Setup

In this section, we describe the environment for software simulations, the datasets, and the preprocessing process.

4.1   Simulation Environment

The input and liquid layers are simulated in the Python-based simulator Brian^{[21, 22]}. The classifier is a single-layer perceptron with gradient-based training and a softmax output function. The number of neurons in the perceptron is the same as the number of classes of input patterns. The scripts for SNN simulation, data processing, and the classifier are all implemented in Python3.7 and arranged in a top-level bash script for automation. All software programs are running solely on the CPU. The CPU is Intel Xeon^® W-2175 CPU @ 2.50 GHz. All accuracy values reported in this paper are averaged over five different independent trials.

4.2   Datasets and Data Preprocessing

4.2.1   Datasets

There are two widely studied DVS datasets, namely NMNIST^[20] and IBM DvsGesture^[9]. The NMNIST dataset is a spiking version of the original frame-based MNIST dataset by scanning static images in front of a smoothly moving DVS^[20]. It consists of the same 60000 training and 10000 test samples as the original MNIST dataset. IBM DvsGesture is an 11-class dataset with 1342 instances recorded from 29 subjects under three different lighting conditions.

The standard split of 60000 training samples and 10000 test samples of NMNIST is used with no data augmentation. For IBM DvsGesture, the first 23 subjects with 1078 recordings are chosen as the training set, and the last six subjects with 264 recordings are reserved for out-of-sample validation. In addition, data augmentation of translation, shifting the coordinate of all events left, right, up, or down, is adopted for IBM DvsGesture, resulting in 1078$\times$5 training samples. The presentation time for one example in NMNIST is 300 ms, and the presentation time for one example in IBM DvsGesture is 1400 ms. The two polarities of events in the two datasets are merged into one channel in our experiments.

4.2.2   Dataset Preprocessing

Every pixel in the DVS dataset is represented as an input neuron in Brian^{[21, 22]}, and the address events of the DVS dataset are emitted as spikes by input neurons. Firstly, we apply a neighboring correlation function to filter noise spikes that are not spatiotemporally related to the spikes outputted by other neurons. Brian is a free open-source simulator for spiking neural networks, where the simulation time and memory cost is proportional to the number of timesteps and network complexity. To reduce the time and memory cost, we implement two methods to tune the time resolution and reduce input neurons. Typically, the time resolution of the DVS event is at the magnitude of microsecond. In this work, we apply a refractory filter function to every input neuron, as such one neuron can only spike once during the refractory period. After applying the refractory filter, the simulation timestep is set to be 0.1 ms.

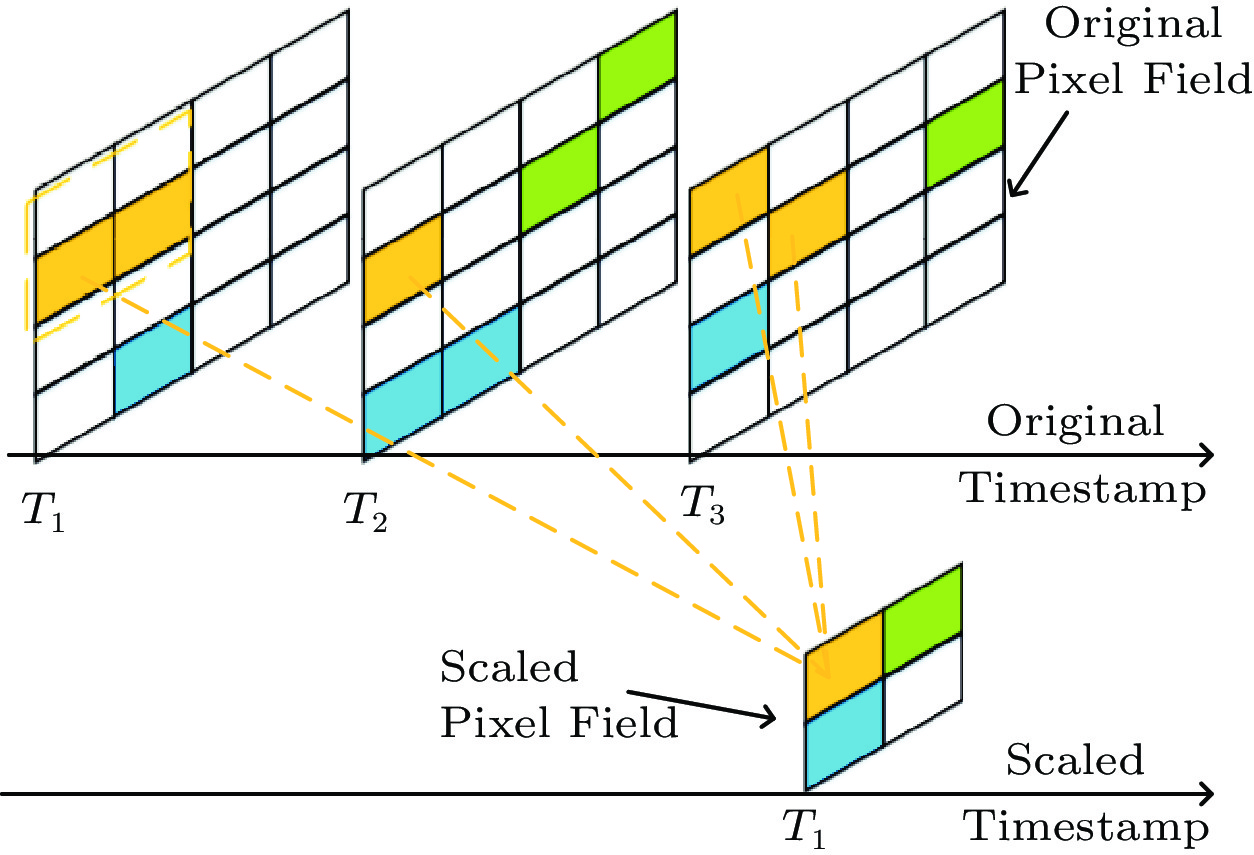
For NMNIST with the pixel size of ${34\times34 }$, 1156 input neurons are needed to be populated to feed the spike train. However, the pixel array of IBM DvsGesture is much larger with the size of $128\times128$, resulting in 16384 input neurons. To this end, we create a pixel-array scaling function to reduce the input size. Taking a scaling factor of $1/4$ as an example, the $128\times128$ pixel array can be scaled into a $64\times64$ pixel array. As shown in Fig.5, the spikes of a $2\times2$ square pixel array are collapsed into one spike at one pixel.

Figure  5.  Schematic of the pixel-array scaling function. The spikes in a 2×2 square pixel array during three timesteps are collapsed into one spike at one pixel.

下载: 全尺寸图片 幻灯片

5.   Experimental Results and Discussion

In this section, we first evaluate the accuracy of the traditional LSM model. Then, the ablation studies are performed to study the effect of the tuning samples and the liquid states. Next, we compare the performance of traditional LSM, and the LSM improved by STDP-tuning, MSF, and the combination of them as well as NAS. Finally, a comprehensive comparison is carried out between LSM and other algorithms for event-based vision recognition.

5.1   Accuracy of Traditional LSM

The fundamental approach to improving the performance of LSM is to increase the number of neurons in the liquid^{[15, 23]}. Firstly, we test the accuracy of the traditional LSM with an increasing number of neurons. Fig.6 presents the test accuracy on NMNIST and IBM DvsGesture. It can be seen that increasing the neuron number can improve the performance to some extent. However, the influence of increasing the neuron number is not always positive. It is because the connectivity also plays a role in affecting the performance, and either high or low connectivity results in accuracy degradation.

Figure  6.  Test accuracy of traditional LSM with the increasing number of neurons.

下载: 全尺寸图片 幻灯片

5.2   Ablation Studies

In this subsection, we utilize two single-liquid LSM with 400 and 800 neurons, respectively.

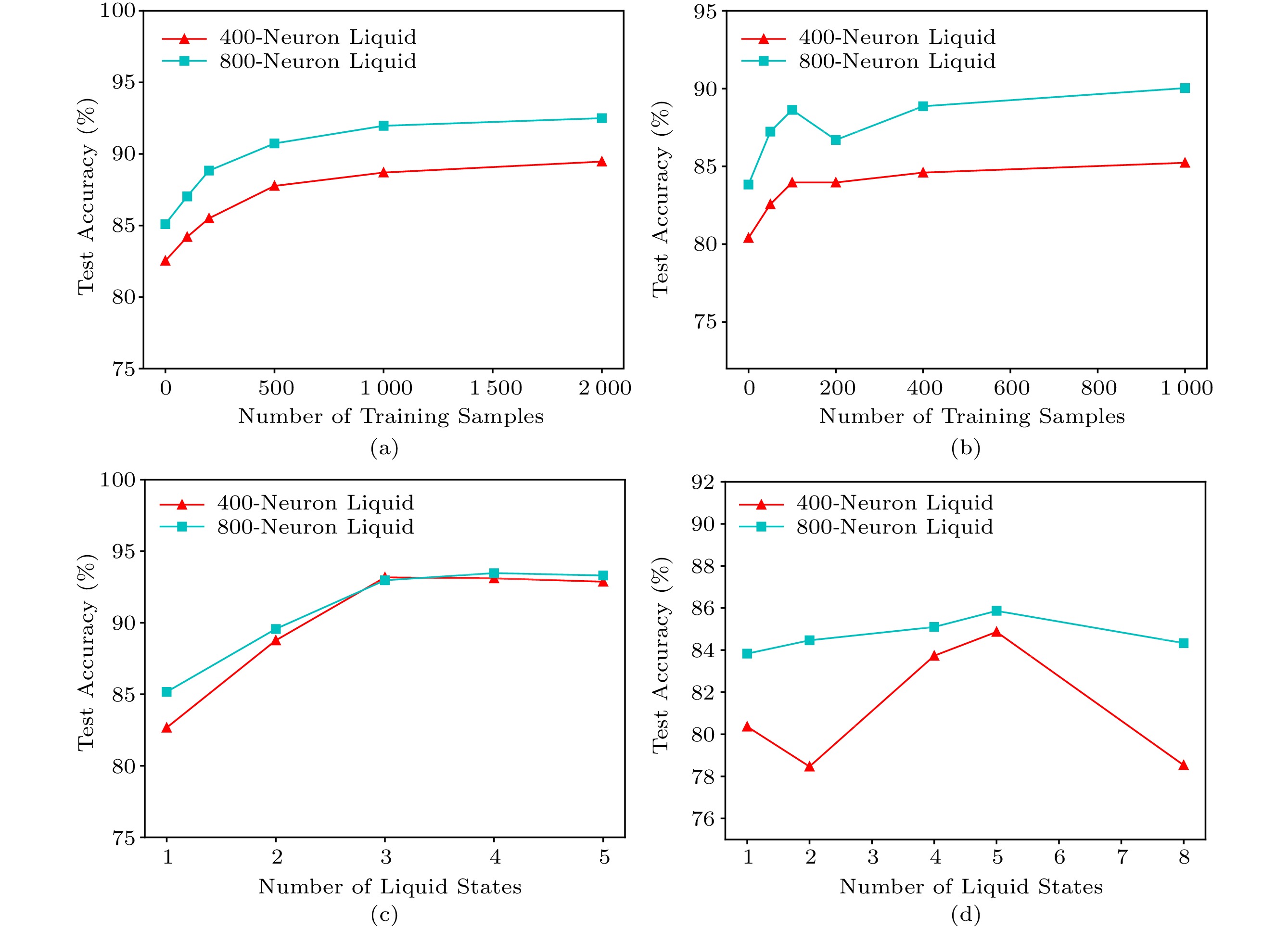
To study the effect of the number of samples for STDP-tuning, we sweep the input training samples from 0 to 2000. As shown in Figs.7(a) and 7(b), by increasing the number of training samples for STDP-tuning, the classification accuracy can be improved by 2%–5%. It can also be seen that 1000 training samples are enough for both NMNIST and IBM DvsGesture to complete the STDP-tuning procedure. Therefore, using only a small part of the training samples for STDP learning, the resulted liquid can be improved in classification accuracy.

Figure  7.  STDP-tuning results. (a) Test accuracy of LSM using different numbers of training samples on NMNIST. (b) Test accuracy of LSM using different numbers of training samples on IBM DvsGesture. (c) Test accuracy of LSM using different numbers of LSs on NMNIST. (d) Test accuracy of LSM using different numbers of LSs on IBM DvsGesture.

下载: 全尺寸图片 幻灯片

To study the effect of the number of LSs (see Fig.3) for classification, we sweep the number of LSs from 1 to 5 for NMNIST and 1 to 8 for DvsGesture. As shown in Fig.7(c), the test accuracy on NMNIST can be improved by MSF where utilizing two LSs increases the accuracy by about 5% compared with using only one LS. There exists an optimal number for the two datasets. As can be seen from Figs.7(c) and 7(d), the optimal LS number for N-MNIST is 4, while the optimal LS number for IBM DvsGesture is 5.

5.3   Performance of Proposed Methods on LSM

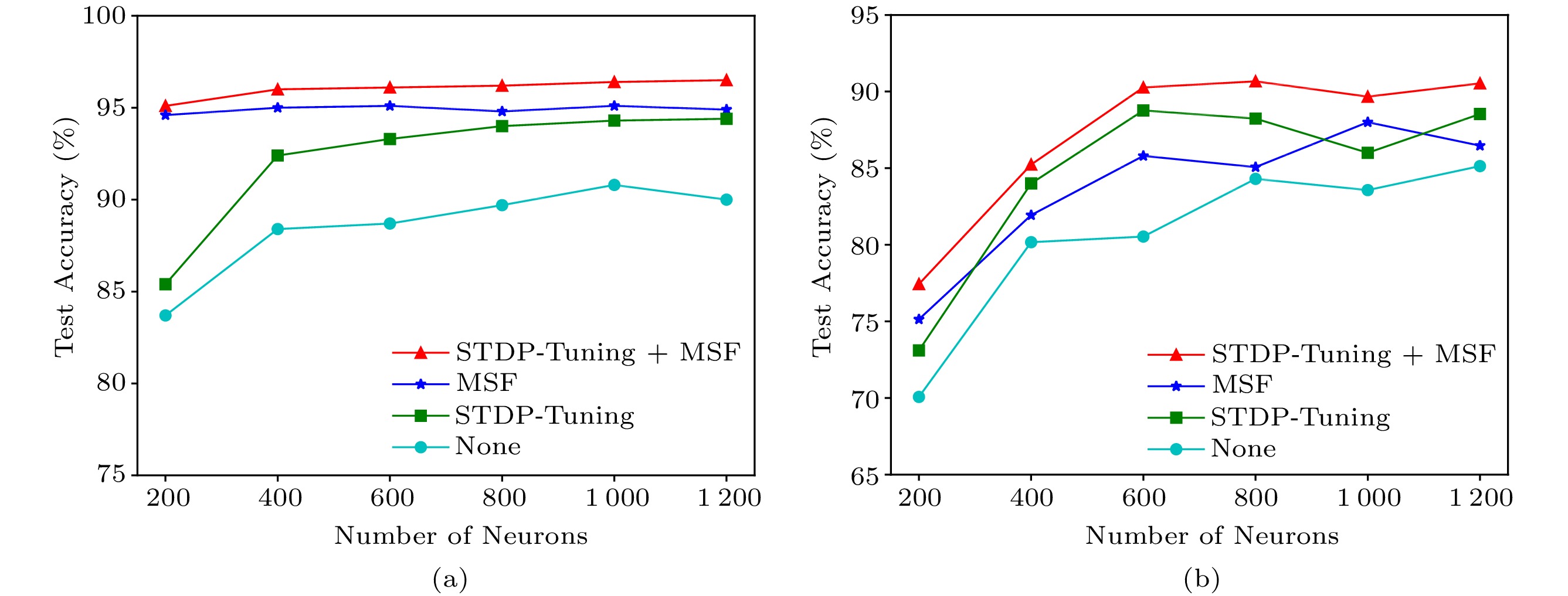
Further, we test the accuracy of a single-liquid LSM under four conditions: the traditional LSM, LSM with only STDP-tuning, LSM with only MSF, and LSM with both STDP-tuning and MSF. As shown in Fig.8, the traditional LSM has the worst performance no matter how many neurons are in the liquid. An interesting observation is that MSF contributes to a much better classification accuracy by nearly 10% increase for NMNIST than STDP-tuning and the traditional LSM when there are only 200 neurons in the liquid. And for DvsGesture, MSF also works better than STDP-tuning with only 200 neurons. This suggests that MSF does have richer information that can be used for classification when the size of liquid is limited, i.e., when the resource budget is limited. And STDP-tuning works better when the input is more complex like the DvsGesture dataset. As a conclusion, STDP-tuning and MSF can be combined to improve the accuracy by 5%–10% for a single-liquid LSM.

Figure  8.  Test accuracy of LSM on (a) NMNIST and (b) IBM DvsGesture with different methods.

下载: 全尺寸图片 幻灯片

5.4   M-LSM Found by NAS

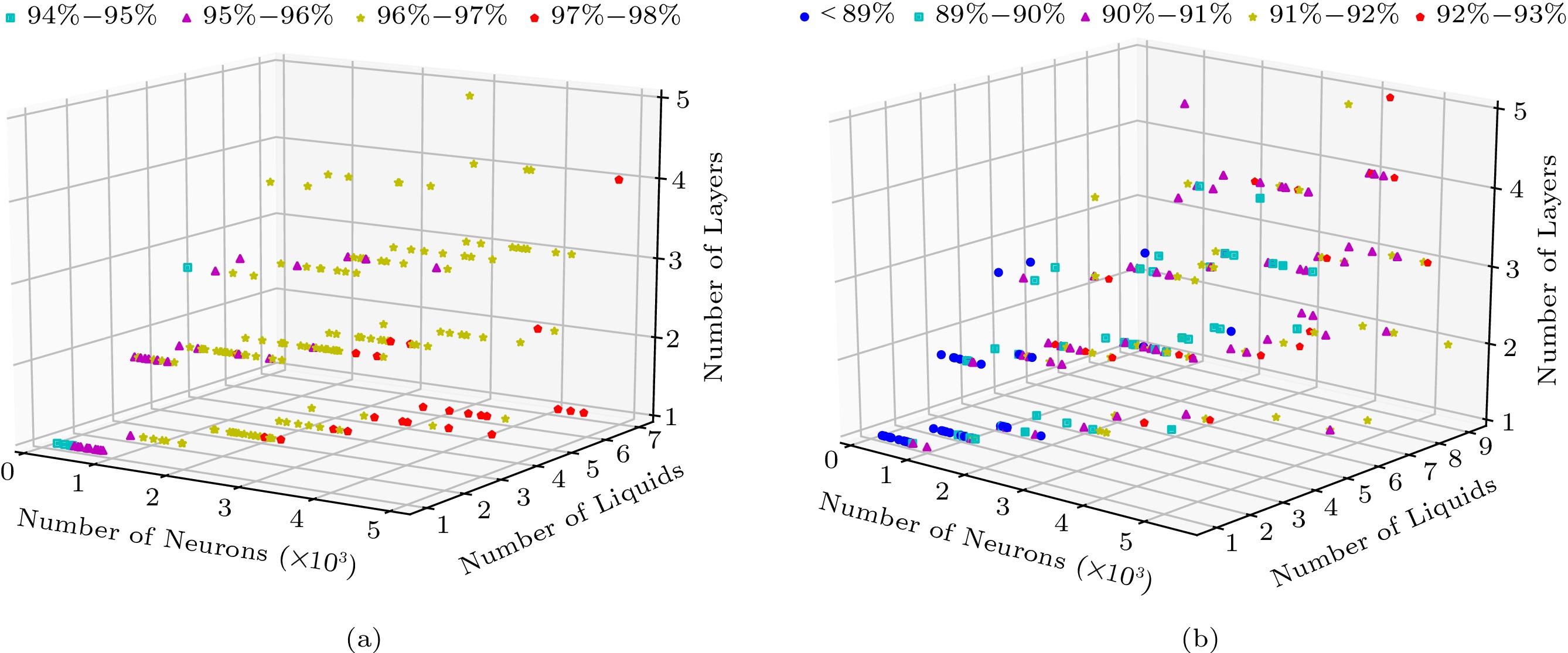
In this subsection, we carry out a NAS-based framework to exploit the architecture potential of LSM with multiple liquids. STDP-tuning and MSF are also implemented in the searched multi-liquid LSM model. In Fig.9, we present the search results of 200 iterations for both NMNIST and IBM DvsGesture. It can be seen that various models can achieve an accuracy of 92% for IBM DvsGesture and 97% for NMNIST, exhibiting the architectural potential of the multi-liquid LSM. We test these high-performance architectures with another five different independent trials, and the average accuracy stays at 92% for IBM DvsGesture and 97% for NMNIST.

Figure  9.  Search results for (a) NMNIST and (b) IBM DvsGesture after 200 search iterations. The accuracy is indicated by different markers. For example, the blue square means the architecture of LSM achieves an accuracy of between 94% and 95%.

下载: 全尺寸图片 幻灯片

As for NMNIST, the performance is more related to the total number of neurons, and most high-performance models belong to the one-layer multi-liquid architecture. However, it differs for IBM DvsGesture. The accuracy on IBM DvsGesture is more sensitive to the architecture rather than the total number of neurons. Especially, the architecture of multi-layer and multi-liquid is more likely to achieve high accuracy. For example, an LSM consists of four liquids, which are arranged in two layers. This LSM contains both sequential and parallel connections among liquids, achieving an accuracy of 92.0% on IBM DvsGesture with only 1500 neurons. Different features of high-performance architectures for the two datasets may be induced by the characteristics of the two datasets. NMNIST is obtained by scanning static images. Therefore, the spatial features of NMNIST are more critical for classification. Differently, IBM DvsGesture is captured by performing gestures in front of DVS and the spatial information varies during a period. In addition to spatial information, the temporal information in IBM DvsGesture is also important for recognition. LSMs with more layers have longer neural connection chains that can reserve time-varying features. To this end, high-performance LSMs for IBM DvsGesture demand the architecture with deeper layers. There are so many hyper-parameters that could affect the performance of the LSM model, and performing exhaustive optimization may lead to higher accuracy. How to find the best architecture with optimal parameters may be the future work for the high-performance LSM.

5.5   Comparison with Event-Based Algorithms

In this subsection, we carry out a comprehensive comparison among several event-based algorithms that achieve high performances on the NMNIST and IBM DvsGesture datasets. Note that each sample in the training dataset only needs to be simulated once.

Table 3 and Table 4 show the accuracy comparison of different methods on NMNIST and IBM DvsGesture, respectively, where Acc. is the accuracy on the test set and Ops/Ts means the number of operations per timestep. As shown in Table 3, the accuracies reported in [13, 14] are 1%–2% higher than those of our M-LSM on NMNIST. However, the high accuracy is at the cost of large network complexity and high training cost. The training cost of our M-LSM is more than 100 times lower than those of [13, 14], indicated by the product of trainable parameters and training epochs. It should be noted that the classifier is only a single-layer perceptron. Compared with [24], the single-liquid LSM with the integration of STDP-tuning and MSF achieves similar accuracy with less network complexity and lower training cost. And the multi-liquid LSM with the two methods achieves 1% higher accuracy.

Table  3.  Comparison of Event-Based Algorithms on NMNIST

Method	Structure	Number of Neurons	Number of Epochs	Number of Synapses	Acc. (%)	Ops/Ts
MLP-SNN[13]	2-layer	512	$\leqslant$100	530000	98.3	$\leqslant$1.00 M
CNN-SNN[14]	3-layer	1000	-	1400000	98.9	-
HMAX-SNN[24]	3-layer	1280	-	25600	96.3	-
Proposed work	Single-liquid	400	1	12800	96.0	$\leqslant$0.13 M
Proposed work	Multi-liquid	1600	1	51200	97.4	$\leqslant$0.50 M

下载: 导出CSV 

| 显示表格

Table  4.  Comparison of Event-Based Algorithms on IBM DvsGesture

Method	Structure	Number of Neurons	Number of Epochs	Number of Synapses	Acc. (%)	Ops/Ts
MLP-SNN[13]	2-layer	512	$\leqslant$100	530000	87.5	$\leqslant$1.0 M
CNN-SNN[13]	8-layer	207306	$\leqslant$100	1100000	93.4	$\leqslant$3.0 M
CNN-SNN[14]	8-layer	-	-	-	93.6	-
CNN-SNN[9]	16-layer	261908	$\leqslant$60000	33604	94.6	-
Proposed work	Single-liquid	600	5	21120	90.4	$\leqslant$0.2 M
Proposed work	Multi-liquid	1500	5	48000	92.0	$\leqslant$0.5 M

下载: 导出CSV 

| 显示表格

As shown in Table 4, the single-liquid LSM could achieve much higher accuracy with about 50 times less training cost compared with MLP-SNN^[13]. We can see that the accuracy achieved by M-LSM is 1%–2% lower than that of CNN-SNNs. However, due to the intrinsic demand for network complexity of CNN, more than 200000 neurons are instanced in [9, 13]. In addition, a GPU-based system is needed for training the network offline, which induces great energy consumption considering a large number of training samples. What is worse, the backpropagation is needed to be performed at every timestep during the training procedure in [9, 14]. The high power consumption induced by the training procedure seriously affects the power advantage of the entire system. Large network complexity and high training consumption are the common disadvantages of CNN-based SNNs. All in all, the proposed M-LSM achieves comparable accuracy on IBM DvsGesture and maintains the superior advantage on network complexity and training cost.

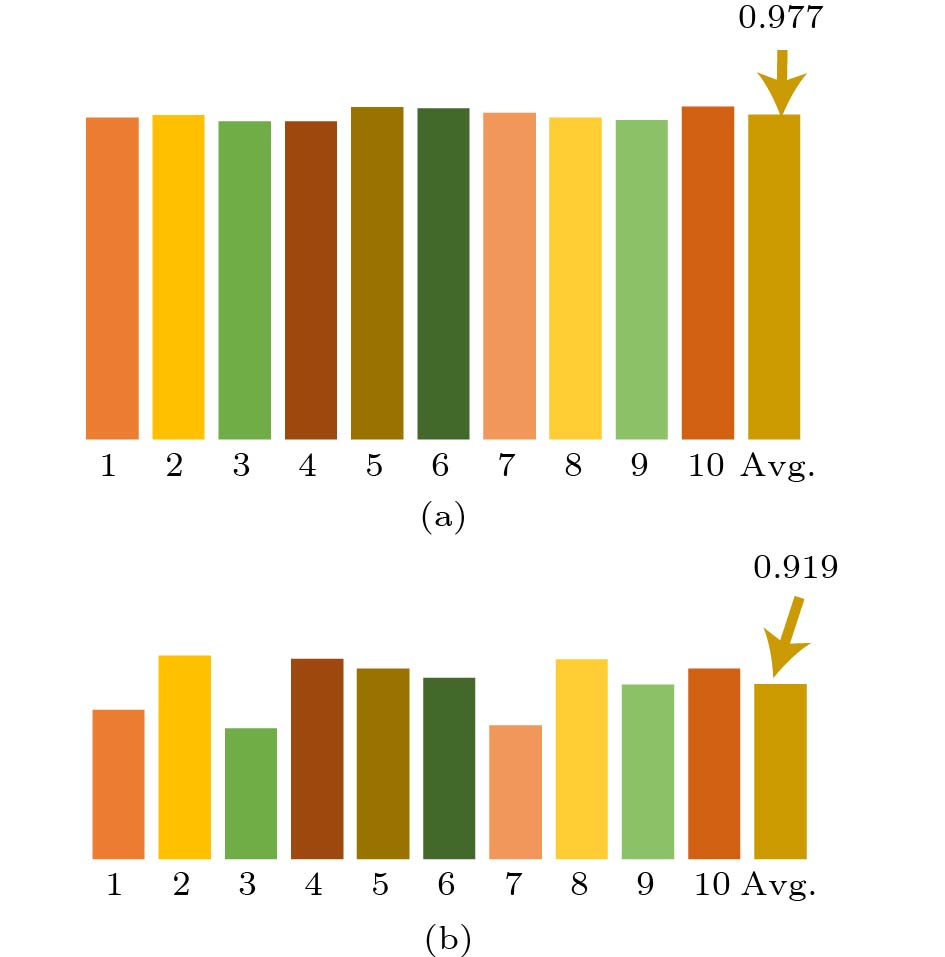
5.6   Cross Validation

To further validate our M-LSM, we conduct the 10-fold cross-validation on the whole dataset for NMNIST and IBM DvsGesture, respectively. Fig.10 shows the test accuracies on each fold and the average accuracy. The accuracies are close to those in Table 4 with small differences because the splitting of the dataset is different. These results show the reliability of our methods.

Figure  10.  Test accuracy of 10-fold cross-validation on (a) NMNIST and (b) IBM DvsGesture. The first 10 bars correspond to the 10 folds' testing accuracies. The last bar (Avg.) reports the average of the 10-fold cross validation testing accuracies.

下载: 全尺寸图片 幻灯片

6.   Related Work

6.1   STDP for Tuning Synapse Weights in LSM

Previously, STDP has been used to tune the synapse weight in different parts of LSM. Wang and Li^[18] introduced STDP to tune the weight in the liquid. Srinivasan et al.^[19] introduced STDP to tune the weight between the input and the liquid. In addition, STDP was used as the learning method to train the classifier in [18]. Differently, in our work, we tune all the synapse weights between input and liquids, and the weights in the liquids. The classifier is still trained by the gradient-based method.

6.2   Design Space Exploration for LSM

Wijesinghe et al.^[23] presented an ensemble method of multiple liquids for the reduction of connections and the improvement of accuracy. A single large liquid was divided into several smaller liquids with no connection among liquids. The ensemble method could be seen as a parallel structure of multiple liquids. Mi et al.^[16] proposed a structure of forwardly-connected multi-liquid to improve the separation capability. Forwardly-connected liquids could be seen as a sequential structure. In our work, we explore the architecture potential of multi-liquid with both parallel and sequential structures.

Some work proposed automatic search frameworks to optimize the hyper-parameters of LSM, such as the number of neurons and connectivity probabilities^{[15, 25]}. Rather than parameter optimization, the search framework proposed in our work is to search the network architecture space.

6.3   Computation Cost

We consider that the computation complexity of LSM is related to the size of the reservoir (synapses $S$ and neurons $N$) and the size of the input. Generally, the bigger the reservoir, the larger the size of the input sample, and the more complex the computation. And the in-memory storage is also positively related to the size of the reservoir and that of the input. The size of an input sample can be represented as $I\times T$ with $I$ input channels and $T$ sampled timesteps.

It is hard to compute the accurate operations for LSM/SNN because the firing process is dynamic. The computing scheme of an SNN is not like that in DNN which is fixed and unchanged for all inputs. The inference computation steps for a neuron of an LSM are mainly the accumulation of the neuron's membrane potential and threshold comparison^[26]. The accumulation process is multiply-and-accumulation (MAC) and thus counted as two operations (ops). The comparison process can be counted as two ops as well, a comparison operation and a potential resetting operation. The training complexity mainly consists of two parts, one is the weights updation using STDP which is complex and counted as 10 ops, and the other is the membrane potential accumulation and updation (4 ops).

To estimate the computational complexity, we consider the worst case for a timestep. For the training of LSM, supposing at a timestep, all of the synapses need to be updated, and all liquid neurons need to update their membrane potential; therefore the total computations would be $10\times S+4N$ ops. For test, it would be $4N$ ops without synapses updation.

As for the DNN-like SNNs^[13], they use the backpropagation inspired methods for training. We count two ops for the synapse weight updation process as it needs to calculate the gradients for two state variables of the neuron. The computations for inference are mainly membrane potential accumulation and updation. We consider the worse case for a timestep to be the same as above. The total computations should be $2S+4N$ ops for training and $4N$ ops for test.

Since the existing DNN-like SNNs have either 100x more neurons or 10x more synapses, it could be concluded that our M-LSM has less training complexity as shown in the last column of Tables 3 and 4 by giving the worst ops/timestep.

7.   Conclusions

In this paper, we proposed to use an enhanced liquid state machine (LSM) for event-based vision recognition. Two methods, namely multi-state fusion and multi-liquid search, were proposed for performance improvement. The resulted M-LSM, an optimized multi-liquid LSM, can achieve comparable classification accuracies on two DVS datasets. A comprehensive comparison study showed that M-LSM can prevail over other event-based algorithms with much smaller network complexity and lower training cost. Considering the speed and power advantages of small network complexity and low training cost, this work provided a competitive solution for event-based vision recognition, especially in power-constrained scenarios.

Acknowledgements

The authors gratefully acknowledge editors and the anonymous reviewers for comments to improve the paper. The authors thank Hong-Guang Zhang, Xun Xiao, Xu-Hu Yu, and Zi-Yang Kang from National University of Defense Technology, Changsha, for their helpful comments.