1.   Introduction

Nowadays social networks are becoming more and more popular. Smart phones enable anyone to dispose their online social networks anytime and anywhere. Therefore, it is not hard to see that one's online social circle is much bigger than one's physical social circle. Sintos and Tsaparas^[1] thought that the social circle of the ordinary user contains not only true friends, but also forgotten high-school classmates, distant relatives, and acquaintances made by brief encounters. Therefore, many online connections correspond to weak connections, or non-relationships in the physical world. Sintos and Tsaparas^[1] proposed to use the notion of Strong Triadic Closure (STC)^[2] for this problem. They defined the problem of MinSTC (Minimum Weakness STC)/MaxSTC (Maximum Strength STC), which is to label the ties of a social network as weak or strong so as to enforce the STC property and minimize/maximize the number of weak/strong ties. By reducing MinSTC to the vertex cover problem, they proved that the MinSTC problem is NP-hard and presented approximation algorithms for it. Golovach et al.^[3] extended the study of Sintos and Tsaparas^[1]. They initiated the parameterized study of the strong $F$-closure problem, where $F$ is a fixed graph. If $F = P_3$ ($P_3$ is the induced path on three vertices), then the strong $F$-closure problem is equivalent to the MaxSTC problem. They showed that the problem is fixed-parameter tractable with this parameterization for every fixed graph $F$, whereas the problem does not admit a polynomial kernel even when $F = P_3$.

Recently, Grüttemeier and Komusiewicz^[4] have studied the relation of MinSTC and cluster deletion, because STC labeling properties can also be stated in terms of induced subgraphs. That is, for every induced $P_3$ of graph $G$, at least one edge is labeled as weak. Therefore, the cluster deletion problem, which is to destroy all induced $P_3$s by edge deletions, is closely related to MinSTC^[5]. Grüttemeier and Komusiewicz^[4] studied MinSTC from the perspective of parameterized computation, and showed that MinSTC admits a $4k$-vertex kernel. Inspired by Grüttemeier and Komusiewicz^[4], we improve the previous best known problem kernels for both MinSTC and cluster deletion by using some techniques proposed in [6, 7] dealing with the cluster editing problem.

In order to better describe STC and cluster deletion, we quote several definitions from [4].

Definition 1 (Strong Triadic Closure Labeling)^[4]. A labeling $L = (S_{L} ,W_{L})$ of an undirected graph $G = (V, E)$ is a partition of the edge set $E$. The edges in $S_{L}$ are called strong and the edges in $W_{L}$ are called weak. A labeling $L = (S_{L} ,W_{L})$ is an STC labeling if there exists no pair of strong edges $(u,v) \in S_{L}$ and $(v,w) \in S_{L}$ such that $(u,w) \notin E$.

An STC labeling $L$ of a graph $G$ is optimal when the number of weak edges $|W_{L}|$ is minimal. The problem is defined as follows.

Definition 2 (Strong Triadic Closure (STC))^[4].

Input: an undirected graph $G = (V, E)$ and an integer $k \in N$.

Question: is there an STC labeling $L = (S_{L} ,W_{L} )$ with $|W_{L}| \leqslant k$?

Definition 3 (Cluster Deletion)^[4].

Input: an undirected graph $G = (V, E)$ and an integer $k \in \mathbb{N}$.

Question: can we transform $G$ into a cluster graph, that is, a disjoint union of cliques, by at most $k$ edge deletions?

As shown in [5], the terminology of $P_{3}$ links STC and cluster deletion. On the one hand, a cluster graph is a graph without any induced $P_{3}$. On the other hand, in order to meet the STC principle, at least one edge of each induced $P_{3}$ should be labeled as weak. Therefore, any set $D$ of at most $k$ edge deletions that transform $G$ into a cluster graph, directly implies an STC labeling $(E \setminus D, D)$ with at most $k$ weak edges. However, it is interesting to note that there are graphs where the minimum number of weak edges in an STC labeling is strictly smaller than the number of edge deletions that are needed in order to transform them into cluster graphs^[5].

In the past 10 years, cluster deletion and related problems of cluster editing have attracted a lot of attention, because they are important graph modification problems which have prominent applications in various areas such as data mining^[8], machine learning^[9], and computational biology^[10]. The difference lies in that cluster editing allows edge insertion and deletion, but cluster deletion only allows edge deletion. Cluster deletion is NP-hard^[11], but it can be solved in polynomial time on cographs^[12]. Cluster editing was first studied by Bendor et al.^[13]. Fellows^[14] first studied this problem from the perspective of parameterized computation and presented a polynomial-time kernelization algorithm which achieves a kernel with at most 24k vertices. This kernelization algorithm needs to solve an LP formulation of cluster editing. Later, Guo^[6] improved the kernel to 4k by using the critical clique graphs. Chen and Meng^[7] introduced the concept of the editing degree of a vertex, which is helpful to study how similar a critical clique and its neighbors are to a disjoint clique, and is also useful to analyze the touched vertices. In particular, they developed five reduction rules to get a kernel of $2k$ for cluster editing.

STC is relatively a new problem proposed by Sintos and Tsaparas^[1]. It is NP-complete even when restricted to graphs with the maximum degree of 4^[5] and split graphs^[15]. In contrast, STC is solvable in polynomial time when the input graph is bipartite^[1], subcubic^[5], a proper interval graph^[15], or a cograph. Grüttemeier and Komusiewicz^[4] provided a linear vertex kernel of $4k$ for STC. They also studied STC and cluster deletion parameterized by $l = |E|-k$, and showed that both problems are fixed-parameter tractable and unlikely to admit a polynomial kernel with respect to $l$.

Although cluster editing and cluster deletion look similar, they are different. The solution of cluster deletion must be the solution of cluster editing, but the opposite is not true^[4]. Therefore, some techniques for cluster editing cannot be directly used for cluster deletion. Furthermore, there are subtle differences between STC and cluster deletion. As shown in [5], in some cases, the solutions of STC and cluster deletion are quite different. The editing degree proposed in [7] is impressive. We use this concept in analyzing the touched vertices. Our contribution is that we consider critical clique $K$ and its neighbors ${\cal{N}}(K)$ as a whole, instead of separating them. We establish the relationship between $V(K) \cup V({\cal{N}}(K))$ and $E_{G}(V({\cal{N}}(K)),$$V({\cal{N}}^{2}(K)))$, which allows us to bound the number of related vertices more effectively. In addition, in analyzing the kernel of STC (Lemmas 5 and 6), we introduce the concept of edge-disjoint $P_3$s, which enables us to obtain the lower bound number of weak edges in a more concise way. Interestingly, this is also true for cluster deletion, that is, the number of edge-disjoint $P_3$s is also the lower bound number of edges to be deleted in cluster deletion. This further reveals the relationship between cluster deletion and STC. More precisely, based on some techniques proposed in [4, 6, 7] and some methods developed by ourselves in this paper, we have improved the kernels of cluster deletion and STC to $2k$.

2.   Preliminaries

Throughout, we consider finite, undirected and simple graphs. For a graph $G = (V,E)$, let $V(G)$ denote its vertex set and $E(G)$ its set of edges. For $S\subseteq V$, the subgraph induced by $S$, denoted as $G[S]$, is the subgraph of $G$ with vertex set $S$ and edge set $\{(u,v)|u,v\in S,(u,v)\in E\}$. A clique in a graph $G$ is a set $K \in V$ of vertices such that $G[K]$ is complete. A disjoint clique is a clique $K$ in which no vertex is adjacent to any vertex not in $K$. For any vertex $v \in V$, the open neighborhood of $v$ is denoted by $N(v)$, and the closed neighborhood is denoted by $N[v]$. The set of vertices in $G$ which has a distance of exactly $2$ to $v$ is denoted by $N^2(v)$. For any two vertex sets $V_1, V_2 \subseteq V$, let $E_G(V_1, V_2) = \{(v_1, v_2) \in E | v_1 \in V_1, v_2 \in V_2\}$ denote the set of edges between $V_1$ and $V_2$. For any vertex set $V' \in V$, let $E_G(V') = E_G(V', V')$ be the set of edges between the vertices of $V'$. We may omit the subscript $G$ if the graph is clear from the context.

The followings are definitions of critical clique and critical clique graph used in [4].

Definition 4 (Critical Clique)^[4]. A critical clique in a graph $G = (V, E)$ is a clique $K$ where the vertices of $K$ all have the same neighbors in $V \setminus V(K)$, and $K$ is maximal under this property.

For a given graph $G = (V, E)$, there exists a partition ${\cal{K}}$ of the vertex set $V$ such that every $K \in {\cal{K}}$ is a critical clique in $G$^[16]. The critical clique graph is then defined as follows.

Definition 5 (Critical Clique Graph)^[4]. Given a graph $G = (V, E)$, let ${\cal{K}}$ be the collection of its critical cliques. The critical clique graph ${\cal{C}}$ of $G$ is the graph $({\cal{K}}, E_{{\cal{C}}})$ with $(K_i , K_j) \in E_{{\cal{C}}} \iff \forall u \in K_i, v \in K_j : (u, v) \in E$.

For a critical clique $K$, we use ${\cal{N}}(K) =$ ${ \bigcup _{K' \in N_{{\cal{C}}}(K)} K'}$ to denote the union of its neighbor cliques in the critical clique graph and ${\cal{N}}^{2}(K) =$ $\bigcup _{K' \in N^{2}_{{\cal{C}}}(K)} K'$ to denote the union of the critical cliques at the distance of exactly 2 from $K$. And we use $V(K)$ to denote the set of vertices of $G$ contained in the critical clique $K$, $V({\cal{N}}(K))$ to denote the set of vertices of $G$ contained in ${\cal{N}}(K)$, and $V({\cal{N}}^2(K))$ to denote the set of vertices of $G$ contained in ${\cal{N}}^2(K)$. The critical clique graph can be constructed in $O(n + m)$ time^[16].

The theory of parameterized computation and complexity mainly considers decision problems (i.e., problems whose instances only require a yes/no answer). A parameterized problem $Q$ is a decision problem (i.e., a language) that is a subset of $\Sigma^*\times N$, where $\Sigma$ is a fixed alphabet and $N$ is the set of all nonnegative integers. Thus, each element of $Q$ is of the form $(x, k)$, where the second component, i.e., the integer $k$, is the parameter. We say that an algorithm $A$ solves the parameterized problem $Q$ if on each input $(x, k$), the algorithm $A$ can determine whether $(x, k)$ is a yes-instance of $Q$ (i.e., whether $(x, k)$ is an element of $Q$). We call the algorithm $A$ a parameterized algorithm if its computational complexity is measured in terms of both the input length $|x|$ and the parameter value $k$. The parameterized problem $Q$ is fixed-parameter tractable if it can be solved by a parameterized algorithm of running time bounded by $f(k)|x|^c$, where $f$ is a computable function and $c$ is a constant independent of both $k$ and $|x|$.

Kernelization is one of the most important techniques used in the development of efficient parameterized algorithms. Let $Q$ be a parameterized problem and $(x, k)$ be an instance of $Q$. An algorithm $K$ is called a kernelization algorithm of $Q$ if $K$ satisfies the following conditions: 1) $K$ transforms $(x, k)$ into the reduced instance $(x', k')$ in polynomial time; 2) $(x, k)$ is a yes-instance of $Q$ if and only if $(x', k')$ is a yes-instance of $Q$; and 3) $|x'|\leqslant g(k)$ and $k'\leqslant k$, where $g(k)$ is a computable function. Correspondingly, the problem $Q$ is called kernelizable and the reduced instance $(x', k')$ is called a kernel. In particular, $Q$ is said to admit a polynomial kernel if $g(k)$ is a polynomial function on $k$. One of the most important theorems of parameterized computation is that a parameterized problem is fixed-parameter tractable if and only if it is kernelizable. The reduced kernel is not only helpful for parameterized algorithms, but also helpful for approximation algorithms (for more on parameterized complexity, please refer to [17, 18]).

3.   Kernelization for Cluster Deletion

Now we discuss the kernelization for the cluster deletion problem. In our algorithms, we make use of the concepts of critical clique and critical clique graph as introduced in [19]. These concepts are also used for kernelization for cluster editing^{[6, 7]} and STC^[4].

Because of the close relationship between cluster deletion and STC, some conclusions about cluster deletion are also valid for STC. Therefore, to avoid repetition, STC will also be discussed when introducing some lemmas about cluster deletion in this section.

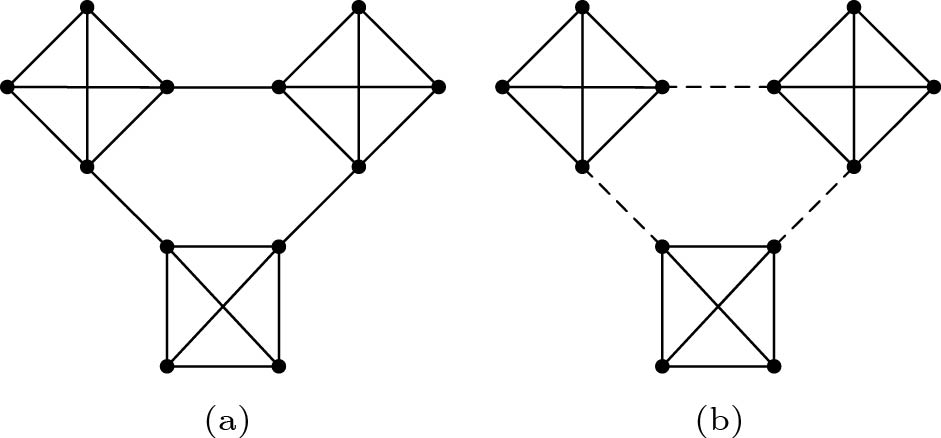
We distinguish between two types of critical cliques as in [4]. We say that a critical clique $K$ is open if $V(K) \cup V({\cal{N}}(K))$ does not form a clique in $G$, and $K$ is closed if $V(K) \cup V({\cal{N}}(K))$ forms a clique in $G$.

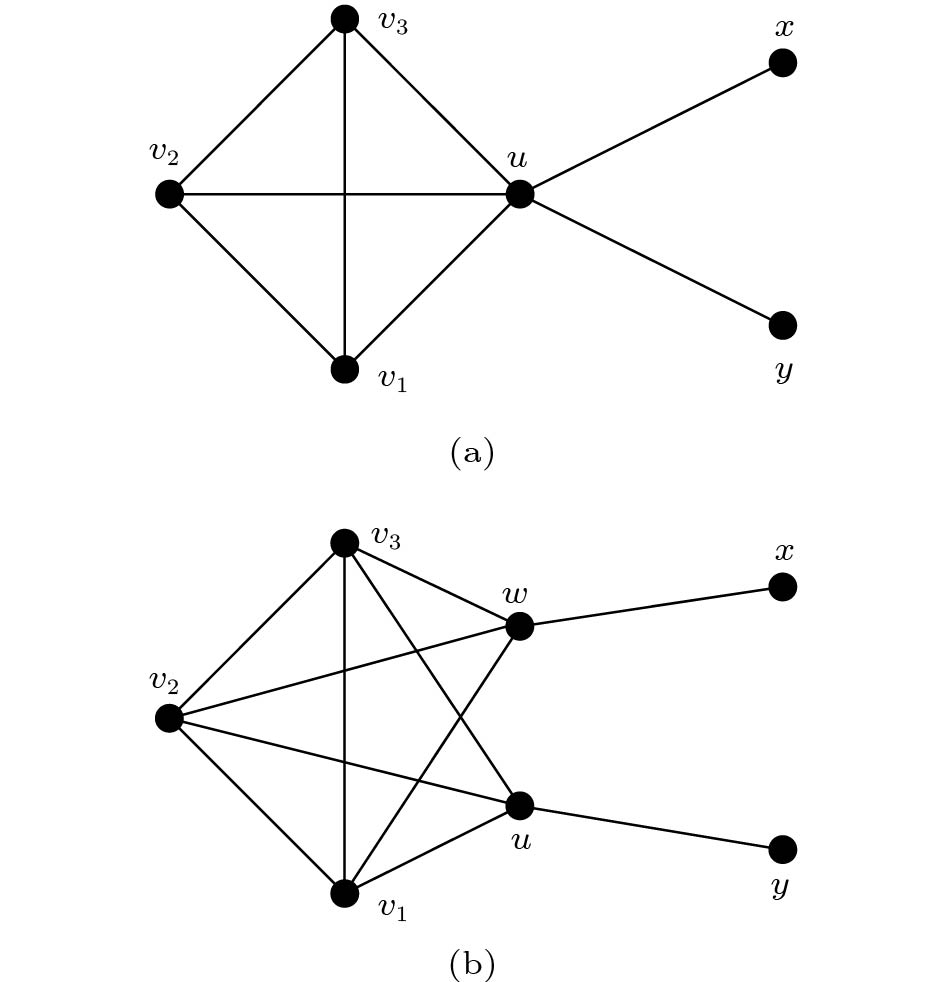
For example, in Fig.1(a), $v_1$, $v_2$, and $v_3$ form a closed critical clique, while in Fig.1(b), $v_1$, $v_2$, and $v_3$ form an open critical clique.

Figure  1.  Critical clique. (a) $v_1, v_2$, and $v_3$ form a closed critical clique. (b) $v_1, v_2$, and $v_3$ form an open critical clique.

下载: 全尺寸图片 幻灯片

Let $E_{\rm{opt}}$ be an optimal solution of cluster deletion for graph $G$ such that $E_{\rm{opt}}$ contains no more than $k$ edge deletions. We say that a vertex $v$ in $G$ is touched (by $E_{\rm{opt}}$) if in the solution $E_{\rm{opt}}$ at least one deleted edge is incident to $v$. Otherwise, vertex $v$ is untouched.

Similarly, for the STC problem, we say that a vertex $v$ in $G$ is touched (by $E_{\rm{opt}}$) if in the solution $E_{\rm{opt}}$ at least one weak edge is incident to $v$. Otherwise, vertex $v$ is untouched.

By dividing the vertices into touched and untouched classes, it is easy to bound the number of touched vertices. Because the optimal solution $E_{\rm{opt}}$ contains no more than $k$ deleted edges, then these deleted edges can touch no more than $2k$ vertices. Therefore, it remains to bound the number of untouched vertices.

Now we introduce several useful properties about critical cliques.

Lemma 1^[6]. There is no optimal solution set $E_{\rm{opt}}$ for the optimization version of cluster deletion on $G$ that splits a critical clique of $G$. That is, every critical clique is entirely contained in one clique in $G_{\rm{opt}} = (V, E \setminus E_{\rm{opt}})$ for every optimal solution set $E_{\rm{opt}}$.

There is a little difference between Lemma 1 and its original version in [6], which studies a different problem called cluster editing. However, the correctness of Lemma 1 is intuitive, because edges within a critical clique do not belong to any induced $P_3$. Thus, edges within a critical clique will not be deleted in any optimal solution for cluster deletion.

Lemma 1 is also true for STC. According to Definition 1, a labeling $L = (S_{L} ,W_{L})$ is an STC labeling if there exists no pair of strong edges $(u,v) \in S_{L}$ and $(v,w) \in S_{L}$ such that $(u,w) \notin E$. That is, there is no induced $P_3$ whose two edges are both labeled as strong. But edges within a critical clique do not belong to any induced $P_3$. Therefore, it is safe to label edges within a critical clique as strong. That is, edges within a critical clique can always be labeled as strong and only edges between critical cliques can be considered for labeling as weak.

Fig.1 also shows two examples of Lemma 1. In Fig.1(a) and Fig.1(b), $v_1, v_2$, and $v_3$ form a critical clique, and edges within these critical cliques do not belong to any induced $P_3$.

Therefore, either in cluster deletion or in STC, we do not need to consider edges within critical cliques. We only need to consider edges between critical cliques.

Lemma 2^[4]. Let $K$ be an open critical clique of $G$, and $E_{\rm{opt}}$ be an optimal solution of cluster deletion for graph $G$. Then each vertex in the open critical clique $K$ must be a touched vertex according to $E_{\rm{opt}}$.

The correctness of Lemma 2 is also intuitive. If $K$ is an open critical clique, then $V(K) \cup V({\cal{N}}(K))$ does not form a clique in $G$. Supposing there are two vertices $u,w \in V({\cal{N}}(K))$ with $(u,w) \notin E$, for each vertex $v \in V(K)$, the edges $(u,v)$ and $(v,w)$ form an induced $P_3$. That is, for each vertex $v \in V(K)$, it is the middle vertex of an induced $P_3$. It follows that either $(u,v)$ or $(v,w)$ should be deleted; thus vertex $v$ must be touched by at least one deleted edge.

Lemma 2 is also true for STC. For each vertex $v$ in any open critical clique, $v$ is the middle vertex of an induced $P_3$. According to Definition 1, the two edges of an induced $P_3$ cannot be labeled as strong at the same time. Therefore one of the two edges must be labeled as weak, and then the middle vertex of an induced $P_3$ must be touched by as least one weak edge. That is, each vertex in any open critical clique must be touched by at least one weak edge.

Fig.1(b) shows an example of Lemma 2. In Fig.1(b), $v_1, v_2$, and $v_3$ form an open critical clique. Each $v_i$ $(i = 1,2,3)$ must be a middle vertex of an induced $P_3$, like $u-v_i-w$. Therefore, $v_i$ must be touched both in cluster deletion and in STC.

As mentioned by Grüttemeier and Komusiewicz^[4], the $4k$-vertex kernel for cluster editing proved by Guo^[6] directly gives a $4k$-vertex kernel for cluster deletion, even though this is not claimed explicitly. In fact, the following reduction rule will lead to a $4k$ kernel.

Let $(G,k)$ be an instance of cluster deletion, and let $K$ be a critical clique in graph $G$.

Rule 1. If $G$ has a closed critical clique $K$ with $|V(K)| > |V({\cal{N}}^{2}(K))|$, then remove $V(K)$ and $V({\cal{N}}(K))$ from $G$ and decrease $k$ by $|E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$.

Lemma 3. Rule 1 is safe.

Theorem 1. Cluster deletion admits a $4k$-vertex-kernel.

By using the techniques in [4, 6], it is not difficult to prove the correctness of Lemma 3 and Theorem 1.

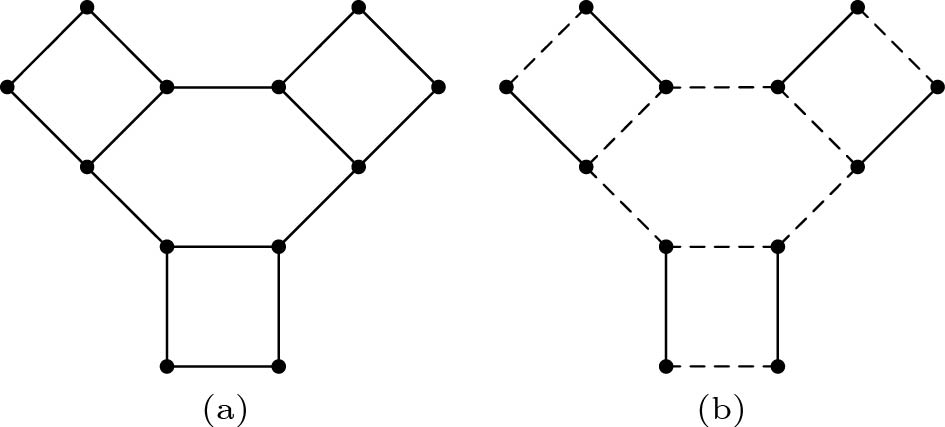
Unfortunately, Rule 1 cannot lead to a kernel better than $4k$, Fig.2 is an example of $4k$ kernel of cluster deletion, which cannot be reduced by Rule 1.

Figure  2.  A graph, which cannot be reduced by Rule 1, is a $4k$-vertex kernel of cluster deletion. (a) Graph. (b) Optimal solution where three dashed edges are deleted.

下载: 全尺寸图片 幻灯片

To achieve a better kernel, we have to develop more complex reduction rules, that is, taking a closed critical clique $K$ and its neighborhood ${\cal{N}}(K)$ together rather than analyzing them separately.

Rule 2. If $G$ has a closed critical clique $K$ with $|V(K)|+|V({\cal{N}}(K))| > |E_G(V({\cal{N}}(K)),V({\cal{N}}^{2}(K)))|,$ then remove $V(K)$ and $V({\cal{N}}(K))$ from $G$ and decrease $k$ by $|E_G(V({\cal{N}}(K)),V({\cal{N}}^{2}(K)))|$.

Lemma 4. Rule 2 is safe.

Proof. Let $K$ be a closed critical clique with

$|V(K)|+|V({\cal{N}}(K))| > |E_G(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$.

Supposing some critical cliques $K_1,K_2,\ldots,K_r$, $(K_1,K_2,\ldots,K_r \in {\cal{N}}(K))$ do not form a clique with $K$ in the optimal solution, let $|V(K)|+|V({\cal{N}}(K))| = n$, $|\cup^r _{i = 1} V(K_i)| = m$; thus, $0<m<n$. Then edges between $\cup^r _{i = 1} V(K_i)$ and $(V(K) \cup V({\cal{N}}(K))) \setminus \cup^r _{i = 1} V(K_i)$ must be removed, that is, $m\times (n-m)$ edges have to be removed. We now discuss it in two cases.

Case 1. If $m\neq 1$ and $m\neq n-1$ $(0<m<n)$, it is obvious that $m\times (n-m)\geqslant n$. We have,

Thus, if we keep the $m\times (n-m)$ edges and delete all edges of $E_G(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))$, we can get a better solution.

Case 2. If $m = 1$ or $m = n-1$, then we have,

It means that if we keep the $m\times (n-m)$ edges and delete all edges of $E_G(V({\cal{N}}(K)),V({\cal{N}}^{2}(K)))$, we can get a solution at least as good as the previous solution. By combining case 1 and case 2, it is safe to conclude that if $|V(K)|+|V({\cal{N}}(K))|>|E_G(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$, then $V(K) \cup V({\cal{N}}(K))$ forms a clique in the optimal solution. Therefore, we can remove $V(K)$ and $V({\cal{N}}(K))$ from $G$ and decrease $k$ by $|E_G(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$.□

The implementation of Rule 2 is very straightforward. Firstly, we construct the critical clique graph of $G$; secondly, we find out a closed critical cliques $K$ in the critical clique graph; thirdly, we check whether $|V(K)|\;\;+\;\;|V({\cal{N}}(K))|\;\; >\;\;|E_G(V({\cal{N}}(K)),\;V({\cal{N}}^{2}(K)))|$; fourthly, we apply Rule 2 and update the graph, and then repeat the previous steps until no more application of Rule 2 is possible. The running time of Rule 2 is not larger than $O(|V|^3)$.

Theorem 2. Cluster deletion admits a $2k$-vertex kernel.

Proof. Let $E_{\rm{opt}}$ be the optimal solution, denoted by $p_0(v)$ the number of edges incident to $v$ that are deleted by the solution $E_{\rm{opt}}$.

We partition the vertices of $G$ into two parts. $V_1$ consists of untouched vertices and all their touched neighbours, and $V_2$ consists of the rest touched vertices that are not contained in $V_1$.

For convenience, we use ${\cal{K}}_{{\cal{UC}}}$ to denote the set of untouched closed critical cliques, and thus we have,

$\qquad\qquad V_1 = \bigcup_{K \in {\cal{K}}_{{\cal{UC}}}}(V(K)\cup V({\cal{N}}(K)))$.

In addition, we use ${\cal{K}}_{\cal{R}}$ to denote the set of the rest touched critical cliques that are not contained in $V_1$, thus,

$\qquad\qquad\qquad\qquad V_2 = \bigcup_{K \in {\cal{K}}_{{\cal{R}}}}V(K)$.

We first consider vertices of $V_1$. According to Lemma 2, vertices in any open critical clique must be touched vertices in the resulting cluster graph. Therefore the untouched vertices must come from the closed critical cliques in the input graph. Let $K$ be such a closed critical clique in the input graph. Thus, in the resulting cluster graph, all vertices in $K$ become untouched vertices. Thus all edges between $V(K)$ and $V({\cal{N}}(K))$ will be kept, and all edges between $V({\cal{N}}(K))$ and $V({\cal{N}}^2(K))$ will be deleted. Because graph $G$ is reduced by Rule 2, so we have $|V(K)|+ |V({\cal{N}}(K))| \leqslant |E_G(V({\cal{N}}(K)),V({\cal{N}}^{2}(K)))|$, which means we have

In the equation above, all edges between $V(K)$ and $V({\cal{N}}(K))$ are kept, and all edges between $V({\cal{N}}(K))$ and $V({\cal{N}}^2(K))$ are deleted, as a result,

$|E_G(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))| = \sum\nolimits_{v \in V({\cal{N}}(K))} p_0(v)$.

Then we get,

Second, we consider the rest touched vertices in the touched critical cliques. Let $K$ be such a touched critical clique. Each vertex in $K$ must be incident to at least one deleted edge. Therefore we must have

And we get,

Finally, we have

Since each deleted edge in the optimal solution $E_{\rm{opt}}$ increases $p_0(v)$ by 1 for exactly two vertices in graph $G$, the value $\sum\nolimits_{v \in V} p_0(v)$ is bounded by twice the number of deleted edges in $E_{\rm{opt}}$. If $E_{\rm{opt}}$ contains no more than $k$ deleted edges, there should be no more than $2k$ vertices.□

4.   Kernelization for STC

Although STC looks like highly the same as cluster deletion, their optimal solutions are not the same in many cases. According to Lemma 2, we can easily bound the number of vertices in open critical cliques, as we do in dealing with cluster deletion. Thus, we still need to bound the number of vertices in closed critical cliques.

Considering the vertices of closed critical clique probably become vertices not incident to any weak edges in the optimal STC-Labeling, we cannot bound the number of vertices of closed critical clique directly. Therefore, we have to treat the closed critical clique $K$ and its neighbours ${\cal{N}}(K)$ as a whole.

Before presenting the reduction rule, we give an important new lemma described as follows.

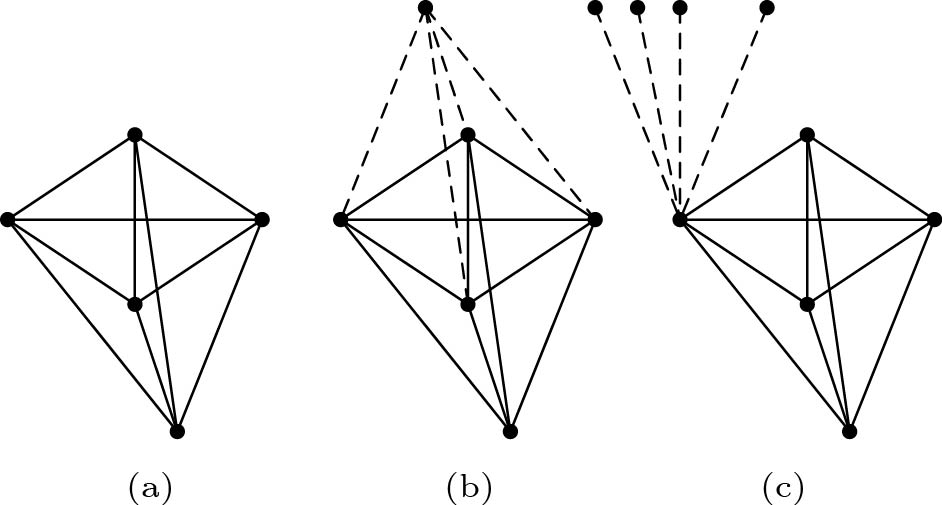
Lemma 5. Given a clique $C$ of size of $n$, we assume one adjoins $m$ $(m \leqslant n-1)$ edges to at most $n-1$ vertices of $C$, and only one end of each edge is incident to a vertex of $C$. Then, these $m$ edges must form $m$ edge-disjoint $P_3$s with edges within clique C.

Proof. It is worth noting that with $m \leqslant n-1$, there must be at least one vertex of $C$ which is not incident to any newly added edge. Without loss of generality, let $u$ be a vertex which is not incident to any newly added edge. Now we discuss the newly added edges in two cases.

Case 1. When we adjoin a new edge to a vertex $v$ of $C$, and $v$ is a vertex which is not incident to any newly added edge before, then the new edge and edge $(u,v)$ will form an induced $P_3$.

Case 2. When we adjoin a new edge to a vertex $v$ of $C$, and $v$ is already incident to some newly added edges, the new edge will form an induced $P_3$ with edge $(v,w)$ ($w$ is a vertex of $C$ other than $u$). Because there are $n-1$ edges of $C$ incident to $v$, at most $n-1$ newly added edges can be incident to $v$. Correspondingly, we can always find $n-1$ edge-disjoint $P_3$s related to $v$.

The worst cases are shown in Fig.3. In Fig.3(b), all the $m = n-1$ newly added edges are incident to $n-1$ different vertices of $C$. In Fig.3(c), all the $n-1$ newly added edges are incident to only one vertex of $C$. In these two cases, we can just find $n-1$ edge-disjoint $P_3$s containing $n-1$ new edges, there is no redundancy.□

Figure  3.  Worst cases of Lemma 5. Four new edges (dashed) are incident to a clique of five vertices. (a) A clique $C$ of five vertices. (b) All four edges incident to different vertices. (c) All four edges incident to only one vertex.

下载: 全尺寸图片 幻灯片

In fact, if we adjoin $m$ $(m \leqslant n-1)$ edges to at most $n-1$ vertices of $C$ (the size of $C$ is $n$), there is at least one vertex not incident to any of the newly added edges. Therefore, vertices of clique $C$ can be partitioned into two sets. One set includes vertices which are not incident to any of the newly added edges. These vertices form a critical clique $K$. The other set includes the rest vertices that are incident to the newly added edges, which can be seen as the neighbours of the critical clique $K$, denoted by ${\cal{N}}(K)$. In addition, vertices incident to the other end of the newly added edges can be seen as 2-order neighbours of $K$, that is, ${\cal{N}}^2(K)$.

Now, it is time to present the reduction rule.

Rule 3. If $G$ has a closed critical clique $K$ with $|V(K)|+|V({\cal{N}}(K))| > |E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|,$ then remove $V(K)$ and $V({\cal{N}}(K))$ from $G$, and decrease $k$ by $|E_{G}(V({\cal{N}}(K)),V({\cal{N}}^{2}(K)))|$.

Rule 3 does the same thing as Rule 2, but the proof of its correctness is quite different.

Lemma 6. Rule 3 is safe.

Proof. Let $K$ be such a closed critical clique with

$|V(K)|+|V({\cal{N}}(K))| > |E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$.

Then $V(K)$ and $V({\cal{N}}(K))$ form a clique, and there are at most $(|V(K)|+|V({\cal{N}}(K))|)-1$ edges incident to the clique $G[V(K) \cup V({\cal{N}}(K))]$. According to Lemma 5, there are at least $|E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$ edge-disjoint $P_3$s formed by $E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))$ and edges within $G[V(K) \cup V({\cal{N}}(K))]$. In any optimal solution, these edge-disjoint $P_3$s result in $|E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$ weak edges. Considering induced subgraph $G[V(K) \cup V({\cal{N}}(K))]$ and edges of $E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))$, we have to label at least $|E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$ edges as weak edges. Therefore we can label all edges of $G[V(K) \cup V({\cal{N}}(K))]$ as strong edges, and label edges of $E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))$ as weak edges. And this labeling will not affect the subsequent labeling. In addition, $E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))$ forms a weak cut as described in [4], and thus $V(K)$, $V({\cal{N}}(K))$, and $E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))$ can be removed from $G$ safely.

It is worth noting that the proof of Lemma 6 can also be used in cluster deletion, because $|E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$ edge-disjoint $P_3$s also mean at least $|E_{G}(V({\cal{N}}(K)), V({\cal{N}}^{2}(K)))|$ edge deletions are needed to get a cluster. Therefore, the proof of Lemma 6 can replace the proof of Lemma 4. However, the proof of Lemma 4 is simple, and it provides another way to prove the correctness, so we keep it in this paper.□

Theorem 3. STC admits a 2k-vertex kernel.

Proof. Let $E_{\rm{opt}}$ be the optimal solution, denoted by $p_0(v)$ the number of weak edges incident to $v$. Let $K$ be an untouched closed critical clique in the input graph. Thus, in the result STC labeling, all vertices in $K$ become untouched vertices. In this case, each edge of $E_G(V(K),V({\cal{N}}(K)))$ must be labeled as strong edge, and each edge of $E_G(V({\cal{N}}(K)),V({\cal{N}}^2(K)))$ must be labeled as weak. Since each edge of $E_G(V({\cal{N}}(K)), V({\cal{N}}^2(K)))$ forms $P_3$ with an edge of $E_G(V(K), V({\cal{N}}(K)))$, and each edge of $E_G(V(K), V({\cal{N}}(K)))$ is labeled as a strong edge, each edge of $E_G(V({\cal{N}}(K)),V({\cal{N}}^2(K)))$ must be weak. By Rule 3, we have $|V(K)|+|V({\cal{N}}(K))| \leqslant |E_G(V({\cal{N}}(K)),$$V({\cal{N}}^{2}(K)))|$, which means we have

The rest proof of this theorem is similar to that of Theorem 2. Therefore, it is omitted.□

Finally, let us take a look at the effectiveness of Rule 2 or Rule 3. As mentioned earlier, the example in Fig.2 can no longer be reduced by Rule 1. This figure is a $4k$ kernel of the cluster deletion problem. However, if Rule 2 or Rule 3 is applied, it will eventually be reduced to an empty graph, and the reduction process directly gives the optimal solution, either for cluster deletion or for STC.

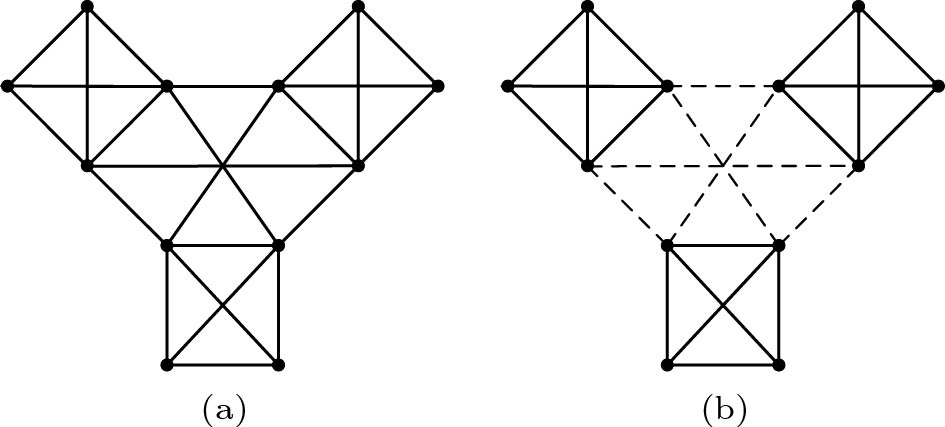
Let us look at another example shown in Fig.4. Obviously, this is a graph that cannot be reduced by Rule 2 or Rule 3. For either cluster deletion or STC, the optimal solution is to delete nine edges (or to label nine edges as weak). There is no doubt that this is a kernel less than or equal to $2k$ ($12 \leqslant 2 \times 9$).

Figure  4.  Kernel less than $2k$. (a) Graph. (b) Optimal solution where nine dashed edges are deleted or labeled as weak.

下载: 全尺寸图片 幻灯片

However, the $2k$ kernel obtained by Rule 2 or Rule 3 is also a tight bound. As shown in Fig.5, this is also a graph that cannot be reduced by Rule 2 or Rule 3. For these two problems, the optimal solution is to delete six edges (or to label six edges as weak), and this is a kernel with the size equal to $2k$ ($12 = 2 \times 6$). Therefore, if we want to get the kernel less than $2k$, we must develop new rules.

Figure  5.  Kernel equal to $2k$. (a) Graph. (b) Optimal solution where six dashed edges are deleted or labeled as weak.

下载: 全尺寸图片 幻灯片

5.   Conclusions

In this paper we addressed the cluster deletion and Strong Triadic Closure (STC). By considering critical clique $K$ and its neighbors ${\cal{N}}(K)$ as a whole, rather than separating them, we established the relationship between the number of vertices related to a critical clique and the number of edges related to the first-order neighbours and the second-order neighbours of the critical clique, which allows us to bound the number of related vertices more effectively. More precisely, we presented $2k$-vertex kernels for both problems. A natural open question is if there is a $(c\times k)$-edge kernel for the problems for a constant $c$.