深度学习训练中的流水线并行训练方法进展
-
摘要:研究背景
以深度神经网络为代表的人工智能技术高速发展,并且在图像分类、语音识别和自然语言处理等诸多领域获得了巨大成功。然而,随着解决问题复杂性的增加,深度学习模型变得越来越复杂,出现了很多参数数量惊人的“大模型”。
目的鉴于流水线并行技术对于加速训练深度神经网络模型(特别是“大模型”)的重要作用和意义,为帮助研究人员全面了解流水线并行相关技术,本文对流水线模型并行进行了全面调查研究。
方法我们在对流水线并行相关技术进行大量调研的基础上,分析总结了流水线并行存在的三大挑战。然后分别从流水线调度、负载均衡和降低流水线并行的计算、存储和通信开销等方面,依次展开对相关关键技术的探讨。
结果在分析完流水线并行技术的三大挑战之后,我们认为设计高效的流水线并行训练方法首先需要同时考虑收敛性和训练速度;同时需要在计算、存储和通信三个方面取得最佳平衡;此外,还需充分考虑并行计算机的体系结构特征,以充分发挥其计算能力。我们给出了流水线并行具有潜在研究意义的两个研究方向,包括通过动态权重预测来同时解决异步流水线并行中存在的权重不一致和权重陈旧问题,以及面向大规模异构计算体系结构的流水线并行。
结论本文对流水线并行训练技术进行了全面综述,涵盖了流水线模型并行的基本概念和主要挑战,还全面比较分析了流水线并行训练方法中的同步和异步流水线调度,并讨论了实现节点内和节点间训练负载平衡的主要技术。此外,还介绍了优化计算、存储和通信的主要技术,并讨论了潜在的研究方向。
-
关键词:
- 深度学习 /
- 流水线调度 /
- 负载均衡 /
- 多GPU系统 /
- 流水线并行(PMP)
Abstract:Deep learning has become the cornerstone of artificial intelligence, playing an increasingly important role in human production and lifestyle. However, as the complexity of problem-solving increases, deep learning models become increasingly intricate, resulting in a proliferation of large language models with an astonishing number of parameters. Pipeline model parallelism (PMP) has emerged as one of the mainstream approaches to addressing the significant challenge of training “big models”. This paper presents a comprehensive review of PMP. It covers the basic concepts and main challenges of PMP. It also comprehensively compares synchronous and asynchronous pipeline schedules for PMP approaches, and discusses the main techniques to achieve load balance for both intra-node and inter-node training. Furthermore, the main techniques to optimize computation, storage, and communication are presented, with potential research directions being discussed.
-
1. Introduction
In the past decade, artificial intelligence technologies, represented by deep neural networks (DNNs), have experienced rapid development and widespread application across various fields, including image and video classification[1, 2], speech recognition[3, 4], language translation[5, 6], and autonomous driving[7, 8]. With the increasing complexity of problem-solving, the scale of DNN model parameters has also grown dramatically to enhance effectiveness. This trend has given rise to deep learning models with tens to hundreds of layers, totaling millions and even billions of parameters, exemplified by models like AmoebaNet[9], Google Neural Machine Translation (GNMT)[5], and Bidirectional Encoder Representations from Transformers (BERT)[10]. Notably, in the field of natural language processing (NLP), there has been a rapid development of large-scale pre-trained language models with a massive number of parameters[11-16], many of which are based on the Transformer[17] architecture. The end of 2022 witnessed the release of DeepMind's conversation model, ChatGPT, further fueling the research interest in large-scale language models.
Numerous studies have shown that the predictive performance of the models improves as deep learning models become more complex and the training dataset grows larger. However, the rapid growth of model sizes and the increasing complexity of neural architectures have raised significant computational challenges. Training large-scale deep learning models with billions of parameters demands not only substantial computational resources but also efficient parallelization techniques. Notably, modern deep learning training still faces the following three significant challenges.
The first challenge stems from the urgent need for computational resources because training “big models” requires a substantial amount of computational resources. The second challenge involves memory limitations, as “big models” typically own a large number of parameters, making storing these parameters in memory during training quite challenging. In stark contrast to the massive number of model parameters in “big models", the storage capacity of GPUs is quite limited. For instance, an NVIDIA GeForce RTX 3090 with 24 GB memory is unable to train GPT-3, which owns 175 billion parameters and requires 700 GB memory consumption with 32-bit storage. Obviously, using a single GPU is usually insufficient to handle such large-scale models, let alone train them effectively. The third challenge is the training time. Training “big models” can be time-consuming because of the huge number of parameters, large-scale datasets (e.g. ImageNet-1K[18] and YouTube-8M[19]), and the complexity of the training process. The training period can span from days to weeks or longer, depending on the model size and available computational resources. For example, training GPT-3 with an NVIDIA V100 GPU would take 288 years[20], an impractical and unacceptable duration.
Data parallelism[21-23] has emerged as the most popular method for accelerating DNN model training, overcoming the computational limitations of a single GPU. Yet, it necessitates replicating the entire model's parameters on each GPU, making it incapable of addressing the storage limitations of a single GPU and rendering it ineffective for training “big models". Unlike data parallelism, model parallelism[24-27] divides the model into several submodels, which are then distributed across different GPUs. Multiple GPUs collaborate to concurrently train each submodel, facilitating parallel training of the model. Therefore, model parallelism can effectively overcome the storage limitations of a single GPU, paving the way for efficient training of large models. When partitioning the DNN model in a layer-wise manner, model parallelism can be further classified into pipeline model parallelism (PMP, also known as pipeline parallelism)[28, 29]. Thanks to its low communication overhead and high efficiency, PMP has been considered as one of the most popular approaches for distributed deep learning training, successfully achieving the goal of efficient training of “big models”.
Several previous surveys have concentrated on algorithms and techniques for distributed deep learning training[30-35], with none of them specifically focusing on the PMP approaches. This survey provides a systematic review of PMP, a typical class of model parallelism and one of the most popular approaches for training “big models”. In Section 2, we outline the three most frequently used parallel training models and further introduce the basic concepts as well as the challenges of PMP. Then, in Section 3, the typical synchronous and asynchronous pipeline schedule approaches are discussed in detail, and a systematic analysis and comparison of these approaches are conducted. Next, in Section 4, the key techniques of achieving load balance for both intra-node and inter-node training are further summarized. We then discuss the main techniques to optimize the computation, storage, and communication of pipeline parallelism approaches in Section 5. Following that, we discuss the promising future research directions for PMP in Section 6. Finally, Section 7 concludes the paper.
2. Preliminary
2.1 Parallel Training Modes
● Data Parallelism. Data parallelism (DP)[21-23, 36] stands out as the most widely used parallel training mode in the deep learning field. Popular deep learning frameworks such as TensorFlow[37], PyTorch[38], and Horovod[39] offer user-friendly APIs to facilitate the training of DNN models using data parallelism. In data parallelism, each GPU is tasked with storing complete and identical model parameters. Different mini-batches of training data are then assigned to specific GPUs. During each iteration of the model parameter update, all GPUs perform synchronized communication, where the gradients generated on each GPU are summed with gradient synchronization strategies like Parameter Server (PS)[40, 41] or global collective communications such as AllReduce[42]. Subsequently, the model parameters are synchronized and updated. Data parallelism involves splitting the training data and leveraging multiple GPUs to train the DNN model in parallel, effectively overcoming the computational limitations of a single GPU, and facilitating deep learning training. However, data parallelism encounters two significant challenges. First, during each time of weight synchronization, the data transferred among GPUs is proportional to the size of the model. Due to frequent weight synchronization among GPUs, data parallelism suffers from excessive inter-GPU communication overhead, hindering its scalability as communication overheads increase with the growth of the model size[43, 44]. Second, data parallelism faces challenges in overcoming the storage limitations of GPUs because it does not alleviate per-GPU memory consumption. It is important to note that, in addition to model parameters, training DNN models also demands a significant amount of GPU memory to store weights, activation values, and other temporary tensor data generated during training[45, 46]. Consequently, when the storage space occupied by model parameters approaches the storage capacity of the GPU, loading the model onto a single GPU for training becomes unfeasible. Even if the model can fit in a GPU, the limited available GPU memory restricts training to small batch sizes, resulting in training inefficiency or under-utilizing computing resources.
● Model Parallelism. Model parallelism (MP) involves partitioning the model across GPUs, assigning each GPU the responsibility for weight updates on specific submodels. Compared with data parallelism, model parallelism offers two key advantages. First, it can overcome the storage limitations of a single GPU through model partitioning. Second, unlike data parallelism, model parallelism does not require transferring the entire model parameters between GPUs during each iteration of parameter update, resulting in significantly lower communication overhead.
Generally, model parallelism can be categorized into two types: intra-layer MP and inter-layer MP. Intra-layer MP, also known as tensor model parallelism (TMP), involves horizontally partitioning the DNN model by splitting the dataflow graph of different operators, such as fully connected layers and convolutional layers. These partitions are then assigned with multiple GPUs, applying each operator to the same batch of training data. Although TMP can overcome the storage limitations of a single GPU and achieve the goal of training “big models” with multiple GPUs, it always hits two roadblocks. First, there is a significant communication overhead, although less than data parallelism, among all GPUs during each iteration of parameter update due to extensive AllReduce operations, leading to high communication costs. Second, especially when training models using a multi-machine multi-GPU system, the InfiniBand network bandwidth between GPU nodes is generally much smaller than the NVLink bandwidth within each GPU node, resulting in inefficient AllReduce operations for each tensor.
Inter-layer MP is widely recognized as pipeline model parallelism (PMP)[28, 29, 31, 47, 48]. The prerequisite for PMP is model partitioning[28, 49], which splits the neural network into consecutive stages each consisting of several consecutive layers. Subsequently, all stages are loaded onto different GPUs, and the DNN model is trained in a pipelined manner across all GPUs. In each complete forward-backward propagation, the frontmost GPU is responsible for reading the training data, performing the forward pass, and sending the output activations to the adjacent GPU. This GPU utilizes the received activations as inputs to conduct the forward pass and continues to send the output to the next adjacent GPU, and so on until the last GPU completes the forward pass. Similarly, in backward propagation, it starts from the last GPU, and each GPU sends the gradients to the previous adjacent GPU until the first GPU completes the backward propagation. In PMP, only the activations and gradients need to be transmitted between adjacent submodels, resulting in much lower communication overhead compared with data parallelism. Currently, PMP has become one of the most effective parallel training approaches for supporting the training of “big models”. Various factors such as GPU utilization, convergence, computation, storage, and communication should be considered to maximize the training efficiency when using the PMP mode on multi-GPU systems.
● Hybrid Parallelism. Hybrid parallelism[31], as the name suggests, combines two or more parallelism modes to harness their advantages to facilitate DNN training. By doing so, it seeks to integrate the advantages of two or more parallel training modes and strike a balance among computation, storage, and communication, enabling the efficient training of large deep learning models. Compared with using a single parallelism mode, hybrid parallelism always enables the following two compelling advantages. First, by combining multiple parallelization modes, hybrid parallelism enables the efficient scaling of model training to large clusters of GPUs, demonstrating better scalability and adaptability than using a single parallelism mode. This is crucial for handling massive datasets and training models with billions of parameters. Second, hybrid parallelism allows for better utilization of available resources with multi-level parallelism, making it better leverage the computational power of modern GPU clusters.
Hybrid parallelism generally encompasses three cases. The first case involves combining DP and TMP. A notable example is that Alex Krizhevsky[50] makes use of hybrid parallelism to parallelize the training of convolutional neural networks. In this case, data parallelism is applied to the convolutional layer, while TMP is applied to the fully connected layers. The second case combines DP and PMP. In this scenario, DNN models are partitioned in a layer-wise manner across GPUs, supporting two or more replicas of DNN models for simultaneous training. Examples of this case include PipeDream[28] and Chimera[47]. The third case of hybrid parallelism involves combining DP, TMP, and PMP (known as 3D parallelism). A representative example is DistBelief[24], which not only distributes neurons in the same layer across machines but also partitions different layers across machines, integrating the features of both TMP and PMP. Additionally, DistBelief supports DP by applying multiple replicas of a model to optimize a single DNN model. Furthermore, the popular deep learning frameworks, such as Megatron-LM[20], DeepSpeed, Colossal-AI[51], and Merak[52], all support 3D parallelism.
2.2 Basic Concepts of PMP
We assume a DNN model consists of L consecutive layers where layer i (1⩽) specifies its model parameters \theta_i . Letting functions f_i and b_i denote the forward pass and backward propagation of the i -th layer, respectively, the forward pass can be represented as F = f_L \circ \ldots f_2 \circ f_1 , and the backward propagation would be B = b_1 \circ \ldots b_{L-1} \circ b_L . In the formal sense, the pipeline parallelism mode splits a DNN model into D consecutive layer blocks \{{\rm{stage}}_1, {\rm{stage}}_2, \ldots, {\rm{stage}}_D\} , satisfying the condition {\rm{stage}}_i \cap {\rm{stage}}_j = \phi , if i\neq j . Each stage is then placed on a specific GPU, and each GPU is responsible for the weight updates of the assigned stage. Two types of intermediate data are required to be transferred between adjacent GPUs: layer outputs for the forward pass and gradients for the backward propagation.
Fig.1(a) depicts the model partition, where a DNN model is divided into three stages, and Fig.1(b) illustrates the pipeline training of mini-batch data with an index of x . In each feedforward-backpropagation round, after a GPU completes its forward step, it needs to wait until all its subsequent GPUs finish their forward and backward steps before it starts its own backward step. This nested arrangement results in the GPU holding an early stage having to wait longer. Whenever a GPU is busy computing, all other GPUs are idle. Therefore, in the naive implementation of PMP (as shown in Fig.1(b)), all the GPUs are active sequentially, one at a time, causing serious under-utilization of the GPUs.
● Computation. For each mini-batch training, the forward pass executes in the order of {\rm{stage}}_1 \rightarrow \ldots \rightarrow {\rm{stage}}_{D-1} \rightarrow {\rm{stage}}_D , followed by the backward propagation, which executes {\rm{stage}}_D \rightarrow \ldots \rightarrow {\rm{stage}}_{2} \rightarrow {\rm{stage}}_1 .
● Storage. Each computing device (e.g., a GPU) should hold the model parameters corresponding to a specific stage. Furthermore, each GPU must maintain all the intermediate variables such as activations and gradients.
● Communication. Inter-GPU communication is iteratively performed during the pipeline training. Each GPU should transmit the activations to the next GPU in the forward direction unless it owns the last layer and transmits gradients to the previous GPU in the backward direction unless it keeps the first layer.
2.3 Challenges in PMP
There are three main challenges in PMP approaches.
● The first and most important challenge is devising an effective pipeline schedule strategy that determines the concurrency and learning efficiency (i.e., the convergence rate and model accuracy) of pipeline training.
● The second challenge is achieving load balance between intra-node and inter-node training, which significantly affects the per-iteration training speed and scalability of pipeline parallelism.
● The last challenge is, to the maximum extent, reducing the costs of computation, storage, and communication, contributing to further boosting the performance of pipeline training.
2.3.1 Effective Pipeline Schedule
Generally, pipeline schedules can be classified into synchronous pipeline schedules and asynchronous pipeline schedules. The adopted pipeline schedule strategy influences both the pipeline structure and the weight update manner, jointly determining the total training time of the DNN model. Let us assume the number of epochs required to train a DNN model to the target accuracy is represented by #epoch, and the training duration for the i -th epoch is denoted as t_i . The whole training time of a DNN model can be represented as t_{\rm{total}} . Then, we have
t_{\rm{total}} = \sum\limits_{i=1}^{\#{\rm{epoch}}}t_i \approx \#{\rm{epoch}}\times \bar{t}, (1) where \bar{t} denotes the averaged training time, i.e., \bar{t}=\sum\nolimits_{i=1}^{\#{\rm{epoch}}}t_i/{\#{\rm{epoch}}} . (1) reveals that the whole training time of a DNN model is determined by both the convergence (or learning efficiency), represented by parameter #epoch indicating the speed at which the model converges, and the iteration speed, represented by parameter \bar{t} indicating the speed at which iterations are performed.
Synchronous pipeline schedule enables the same synchronous semantics as that in data parallelism, hence the focus is solely on improving the iteration speed to decrease the total pipelined training time. For asynchronous pipeline parallelism, it is not only crucial to enhance training speed but also imperative to ensure the learning efficiency of pipeline training. Poor learning efficiency may necessitate a larger number of epochs to achieve the desired accuracy, thereby prolonging the overall training time of the model. Consequently, for an effective pipeline schedule, striking a balance between concurrency and learning efficiency is essential to achieve efficient and effective training, especially for asynchronous pipeline schedules.
2.3.2 Load Balance for Intra-Node and Inter-Node Training
The popular PMP approaches are generally designed for multi-GPU machines[53], which involve two levels of parallelism: intra-node (within a single machine) parallelism and inter-node (between machines) parallelism. Correspondingly, attaining efficient pipeline training should simultaneously consider load balance for both intra-node and inter-node training.
For pipeline training with multi-GPU machines, achieving intra-node load balance requires each GPU to work simultaneously in any given pipeline unit and to spend roughly equal time performing forward and backward propagation calculations. This often requires good model partitioning methods and an effective pipeline schedule. Achieving inter-node load balance requires coordinated efforts from all machines, often necessitating the use of hybrid parallelism. Achieving load balance for intra-node and inter-node training helps give rise to high throughput, enhance the scalability of DNN training, and maximize the utilization of multi-GPU machines.
2.3.3 Optimization of Computation, Storage, and Communication
In the context of pipeline model parallelism, computation, storage, and communication are three of the most important factors affecting the performance and efficiency of DNN training.
During the pipeline training, each GPU proceeds through iterations of forward pass and backward propagation. Optimizing these computations speeds up the iteration procedure. Furthermore, the optimization of computation also includes reducing additional computational overhead beyond forward pass and backward propagation. Throughout the pipeline training period, the GPUs need to store model states which include optimizer states, gradients, and parameters, as well as residual states such as activation[45]. The rapid growth in model size and unbalanced workload may lead to the prevalence of out-of-memory (OOM) errors in pipeline training. For PMP, the optimization of storage mainly includes avoiding unnecessary memory consumption of weights and gradients and decreasing the activation storage cost. Data communication is another critical challenge in pipeline training systems, which is primarily limited by the capacity of high-speed memory, such as high bandwidth memory (HBM) in NVIDIA GPUs. Communication overhead, including inter-GPU communication among pipeline stages and inter-node gradient communication for data parallelism, can be a significant bottleneck in pipeline parallelism. The optimization of communication mainly focuses on avoiding unnecessary communication and hiding the communication with the overlapping of computation.
Notably, simultaneously reducing the computation, storage, and communication costs is quite challenging and often not realistic. It often requires the researchers to find the best tradeoff among computation, storage, and communication to maximize the training efficiency of PMP.
3. Pipeline Schedule for PMP
The schedule manner of a PMP approach actually determines how the model parameters are updated throughout the entire training process. Based on the timing of gradient update, PMP approaches can be roughly classified into two types: synchronous pipeline schedule and asynchronous pipeline schedule.
3.1 Synchronous Pipeline Schedule
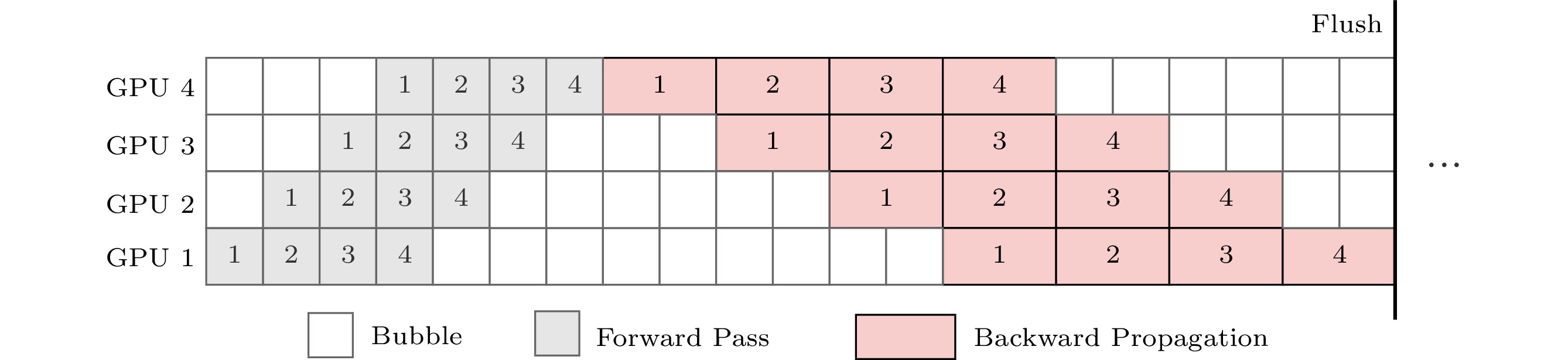
GPipe[29], proposed by Google, is currently one of the most well-known and representative approaches for synchronous pipeline schedules. As shown in Fig.2, a notable characteristic of GPipe is the use of microbatching to reduce the number of bubbles in its pipeline structure and improve GPU utilization. GPipe employs synchronous stochastic gradient descent, with periodic pipeline flushes performed at the end of each mini-batch training. During each iteration, error gradients produced by backpropagation are accumulated across multiple micro-batches, and the model parameters are synchronously updated using the accumulated gradients at each stage. Remarkably, GPipe only stores one version of weights but consumes additional memory for maintaining activations incurred by the microbatching.
Since the introduction of GPipe, pipeline parallelism has gained significant attention and research. Numerous synchronous pipeline structures based on micro-batching have been proposed subsequently, all sharing the common goal of reducing pipeline bubbles and improving concurrency by adjusting the schedule of micro-batches within the pipeline. For example, DAPPLE[48] employs an early backpropagation strategy, in which the last GPU in the pipeline immediately initiates the backpropagation process when it finishes the forward pass of a micro-batch. Another notable feature of DAPPLE is that after the completion of backpropagation, the storage space consumed by storing activation values is released as early as possible. Some pipeline parallelism approaches, such as GEMS[54] and Chimera[47], utilize a dual-pipeline structure in which two versions of weights are trained with the same computational resources. By allowing the two pipelines to be executed in an interleaved manner, these approaches aim to reduce the number of bubbles by filling them with forward or backward computations. However, although the dual-pipeline structure can lessen the number of bubbles in the pipeline structure, it cannot eliminate the inherent bubble overhead in the synchronous pipeline schedules. Moreover, in each iteration, the dual-pipeline mode requires performing AllReduce communication among the GPUs where the symmetric stages of the pipelines are located, followed by synchronizing and updating the model parameters on each stage, resulting in additional communication overhead. Megatron-LM[55] employs the interleaved “1F1B” (One Forward, One Backward) pipeline schedule, where each device in the pipeline is assigned multiple pipeline stages (or model chunks) and, at the same time, each stage requires less computation. The interleaved “1F1B” schedule leads to a smaller size of pipeline bubble. However, the same as GEMS and Chimera, Megatron-LM actually trades a higher communication volume to decrease the pipeline bubbles.
Very recently, zero bubble pipeline parallelism[56] was proposed to achieve zero pipeline bubbles under synchronous training semantics. The key insight of zero bubble pipeline parallelism is to split the backward computation into the gradient computation for the input and the computation for the parameters, and then design a handcrafted schedule to fill the bubbles with computation. A typical case of zero bubble pipeline parallelism is called ZB-H2[56], which uses a sufficient number of micro-batches to fill the pipeline bubbles and achieves a zero bubble schedule.
3.2 Asynchronous Pipeline Schedule
PipeDream[28] is the most representative asynchronous pipeline approach which, for the first time, proposes to employ the “1F1B” schedule (as shown in Fig.3) that allows mini-batches/micro-batches to be trained in an alternating manner with one forward pass followed by one backward propagation. Furthermore, other asynchronous pipeline approaches such as AMPNet[57], PipeDream-2BW[58], SpecTrain[59], XPipe[60], and AvgPipe[61] all employ the “1F1B” schedule. The “1F1B” pipeline execution minimizes the generation of bubbles, resulting in pretty high GPU utilization and fast training speed. However, the interleaved execution of mini-batches in the pipeline, on the one hand, leads to the use of inconsistent weights for each mini-batch/micro-batch's forward and backward passes, thereby affecting the effectiveness of parameter updates. On the other hand, asynchronous updates of model parameters also give rise to the weight staleness issue which refers to the fact that before earlier mini-batches update the weights, latter mini-batches adopt stale weights to derive gradients[59]. The staleness issue hurts the efficiency of DNN training and also could lead to unstable parameter learning. Therefore, a key focus of research in asynchronous pipeline schedules is ensuring the learning efficiency during asynchronous updates of parameters.
Currently, there are two main techniques used to ensure learning efficiency when implementing an asynchronous pipeline schedule: weight stashing and weight prediction. PipeDream[28] is the first to introduce the weight stashing technique, which requires storing one version of weights for each mini-batch that is in progress in the pipeline. This ensures that, at each stage, the forward pass and backward propagation of each mini-batch use the same weights. While this technique effectively resolves the weight inconsistency issue caused by the “1F1B” strategy, it comes with the drawback of requiring additional storage for multiple versions of weights. Moreover, the GPUs located at the front of the pipeline are required to store a larger number of weight versions, resulting in additional and unbalanced GPU memory consumption. To minimize the additional storage overhead incurred by the weight stashing technique, PipeDream-2BW[58] utilizes a technique called double-buffered weight updates (2BW). With the 2BW technique, for a micro-batch that has just entered the pipeline, the latest weights are used for forward pass. Meanwhile, for micro-batches already in the pipeline, 2BW employs the previously cached weights for backward propagation. This technique allows each GPU to maintain only two versions of weights, reducing the storage requirements compared with traditional weight storage techniques used in PipeDream. Furthermore, WPipe[62] proposes double-grouped weight updates (2GW) to achieve better memory efficiency and fresher weight updates than PipeDream-2BW. The 2GW technique divides model partitions into two groups, rearranges the execution order of micro-batches in the first group, and alternatively executes the update of each group. Compared with PipeDream-2BW, WPipe halves both the delayed gradient and memory redundancy. However, although PipeDream, PipeDream-2BW, and WPipe effectively address the issue of weight inconsistency, they do not fully resolve the problem of weight staleness.
Weight prediction is another technique that contributes to ensuring effective learning of model parameters, and can simultaneously alleviate both the weight inconsistency and weight staleness issues caused by asynchronous pipeline schedules. The weight prediction technique is initially proposed and applied to the asynchronous PMP approach SpecTrain[59]. Considering that the smoothed gradient used by the momentum SGD[63, 64] optimizer reflects the update direction of model parameters, SpecTrain, ahead of either forward pass or backward propagation, utilizes the product of the smoothed gradient and the weight version differences to predict the model weights that will be used in future pipeline time steps. Unlike PipeDream and PipeDream-2BW, SpecTrain does not require each GPU to store weights for each active mini-batch in the pipeline. Instead, it simultaneously alleviates the issues of weight inconsistency and weight staleness in asynchronous updates by predicting future weights ahead of both forward pass and backward propagation. However, SpecTrain has significant limitations as it only works well when using momentum SGD to optimize the DNN weights. Another typical asynchronous pipeline schedule approach with the weight prediction technique is XPipe[60], which constructs the weight prediction mechanism based on the Adam[65] optimizer and achieves better learning efficiency compared with momentum SGD used in SpecTrain.
In addition, Yang et al.[66] introduced another asynchronous pipeline-parallel training approach PipeMare which uses learning rate rescheduling and discrepancy correction to improve the statistical efficiency of asynchronous pipeline parallelism. PipeMare can maximize hardware efficiency by avoiding both pipeline bubbles and substantial memory increases. Very recently, the elastic averaging[67] technique has been introduced into the asynchronous pipeline training. This technique has been successfully used by AvgPipe[61] which employs an elastic averaging-based framework to mitigate the bubble issue in GPipe and maintain the statistical efficiency where multiple parallel pipelines are executed and each pipeline handles a batch of data per iteration. To fully overlap communication with computation, AvgPipe uses the technique of advancing forward pass which schedules partial forward pass in advance.
3.3 Comparison
In this subsection, we summarize and compare the typical synchronous and asynchronous PMP approaches. Table 1 lists all the symbols and the corresponding explanations used in this subsection. Table 2 summarizes the framework, basic data unit, and schedule manner of each pipeline approach. It is obvious that all the typical pipeline approaches are implemented on top of either TensorFlow or PyTorch while PyTorch is a more popular choice. Furthermore, the popular pipeline approaches tend to use micro-batch as the basic training data unit.
Table 1. Descriptions of Notations Used in Subsection 3.3Symbol Description D Number of pipeline stages (pipeline depth) P Number of replicated pipelines B Micro-batch size T Number of micro-batches in each mini-batch N Mini-batch size (N=T\times B) M_{\boldsymbol{\theta}} Memory consumption for weights of a stage M_a Memory consumption for activations of a stage Table 2. Summary of Framework, Data Unit, and Schedule Manner of Typical Pipeline Parallelism ApproachesApproach Framework Data Unit Schedule GPipe[29] TensorFlow Micro-batch Synchronous GEMS[54] TensorFlow Micro-batch Synchronous DAPPLE[48] TensorFlow Micro-batch Synchronous Chimera[47] PyTorch Micro-batch Synchronous Megatron-LM[55] PyTorch Micro-batch Synchronous ZB-H2[56] PyTorch Micro-batch Synchronous AMPNet[57] TensorFlow Mini-batch Asynchronous PipeDream[28] PyTorch Mini-batch Asynchronous XPipe[60] PyTorch Micro-batch Asynchronous SpecTrain[59] PyTorch Mini-batch Asynchronous PipeDream-2BW[58] PyTorch Micro-batch Asynchronous PipeMare[66] PyTorch Micro-batch Asynchronous AvgPipe[61] PyTorch Micro-batch Asynchronous WPipe[62] PyTorch Micro-batch Asynchronous Table 3 shows the bubble ratio, convergence trait, weights memory, activations memory as well as whether extra memory, computation, and communication overhead are needed. For each pipeline approach, we assume that each GPU is assigned a specific stage and takes charge of updating the parameters of the corresponding stage. Here we note that we regard the execution of the naive PMP approach shown in Fig.1 as the baseline. The extra communication overhead refers to the extra communication costs other than transmitting activation values and gradient values between adjacent GPUs. The extra computation overhead refers to the extra computations other than performing forward pass, backward propagation, and recomputation[29]. The extra storage overhead refers to the extra memory consumption other than storing a version of weights, activations, gradients, and a copy of optimizer states.
Table 3. Comparisons of Typical PMP ApproachesApproach Bubble Ratio Convergence Weights Memory Activations Memory Extra Mem., Comp., and Comm.^\sharp GPipe (D-1)/(T+D-1) * Excellent M_{\boldsymbol{\theta}} T \times M_a [×, ×, ×] GEMS \approx (D-1)/(D+{1}/{2}) * Excellent 2 M_{\boldsymbol{\theta}} M_a [√, ×, √] DAPPLE (D-1)/(D+T-1) * Excellent M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [×, ×, ×] Chimera (D-2)/(2T+D-2) * Excellent 2 M_{\boldsymbol{\theta}} [ (D/2+1)M_a , D\times M_a ]* [√, ×, √] Megatron-LM (D-1) / (v\times T) ♢ Excellent M_{\boldsymbol{\theta}} T\times M_a [×, ×, √] ZB-H2 ≈ 0% Excellent M_{\boldsymbol{\theta}} (2D-1)\times {M_a} ^\S [×, √, ×] AMPNet ≈ 0% Poor M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [×, ×, ×] PipeDream ≈ 0% Good [ M_{\boldsymbol{\theta}} , D \times M_{\boldsymbol{\theta}} ] [ M_a , D\times M_a ] [√, ×, ×] XPipe ≈ 0% Good† M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, √, ×] SpecTrain ≈ 0% Good‡ M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, √, ×] PipeDream-2BW ≈ 0% Good 2M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, ×, ×] PipeMare ≈ 0% Good M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, √, ×] AvgPipe ≈ 0% Good P \times M_{\boldsymbol{\theta}} [1, D \times T]\times P\times M_a [√, ×, √] WPipe ≈ 0% Good 2M_{\boldsymbol{\theta}} T\times M_a [√, ×, ×] Note: *: concluded by [47]; ♢: concluded by [55], where v denotes the number of chunks on each GPU; †: does not cover all optimizers; ‡: only works well when using momentum SGD as the optimizer; \S : peak activations memory concluded by [56]; \sharp : [√, ×, √] means requiring extra memory consumption and communication but no extra computation, and vice versa. Bubble Ratio. Table 3 reveals that the overwhelming majority of synchronous pipeline approaches, except for the ZB-H2 approach, suffer from bubble overhead. The percentage of bubbles is usually determined by the pipeline depth (i.e., D ) and the number of micro-batches in a mini-batch (i.e., T ). The exceptional case is Megatron-LM, whose bubble ratio also depends on the number of chunks on each GPU (i.e., v ). In contrast, asynchronous pipelined parallel approaches always have a close-to-zero percentage of bubbles, resulting in a GPU utilization close to 100%.
Convergence. As shown in Table 3, all synchronous schedule approaches maintain the same semantics as in model parallelism and enjoy excellent convergence traits superior to that of the asynchronous pipeline approaches. For pipeline parallelism approaches with asynchronous schedules, the convergence trait is dependent on effective parameter learning, especially how the weight inconsistency and staleness issues are addressed. AMPNet[57] executes the “1F1B” without adopting effective measures to alleviate the weight inconsistency and staleness issues, resulting in poor convergence. PipeDream[28], PipeDream-2BW[58], and WPipe[62] address the weight inconsistency issue by additionally storing weights of in-flight mini-batches or micro-batches but leaving the weight staleness issue unsolved. XPipe[60] and SpecTrain[59] simultaneously alleviate the weight inconsistency and staleness issues through weight prediction. Notably, the performance of SpecTrain is quite limited to the momentum SGD optimizer, not well applied to the cases when using other gradient-based optimizers such as RMSprop, Adam, and AdamW. Although XPipe outperforms SpecTrain, its performance is stills limited by the choice of optimizer and does not cover all optimizers. Furthermore, PipeMare[66] and AvgPipe[61] try to achieve effective parameter learning with well-designed techniques, while both of them are unable to ensure exactly the same semantics as that in data parallelism.
Weights Memory. Regarding weight storage overhead, PipeDream consumes the highest and the most unbalanced memory size. The frontmost GPU is required to store D versions of weights, while the last GPU only needs to store one version of weights. The memory consumption of AvgPipe is also comparatively large as AvgPipe requires each GPU to maintain P replicas of stage parameters, where P denotes the number of replicated pipelines. In contrast, GEMS[54], Chimera[47], and PipeDream-2BW require each GPU to hold two versions of weights. WPipe also reaches a peak weight consumption of two versions of weights, despite the fact that the 2GW technique reduces the overall weight memory consumption. GPipe[29], DAPPLE[48], ZB[56], AMPNet[57], XPipe[60], SpecTrain[59], and PipeMare[66] have the lowest weight storage overhead, with only one copy of weights. Similarly, Megatron-LM[55] requires each GPU to store v smaller copies of weight chunks, totaling one copy of weights, where v is the number of chunks on each GPU.
Activations Memory. In terms of activations memory, AvgPipe consumes the most unbalanced memory to store the activation due to the pipeline training of multiple pipeline replicas and the microbatching strategy. GPipe, Megatron-LM, and WPipe rank second which require each GPU to store T activations because of the adopted recomputation technique. GEMS enjoys the lowest activations memory consumption, only requiring each GPU to store one input activations. The special case is Chimera, which highly depends on the pipeline depth. While DAPPLE and the remaining asynchronous approaches generally have activation storage overhead ranging between the interval of M_a and D\times M_a . The point to note is that ZB-H2[56] requires a sufficient number of micro-batches to achieve zero bubbles, thus necessitating a larger activation memory footprint than other PMP approaches with ``1F1B'' schedule (e.g., DAPPLE and Megatron-LM).
Extra Memory, Computation, and Communication. For extra memory consumption, the weight stashing techniques used in PipeDream[28], PipeDream-2BW[58], and WPipe[62] incur extra memory consumption. The bi-directional pipeline techniques used in GEMS[54] and Chimera[47] as well as the multiple pipeline replicas in AvgPipe[61] also incur extra memory consumption. The weight prediction technique used in XPipe[68] and SpecTrain[59] requires extra memory to store the predicted weights. PipeMare[66] also requires using a bit of extra memory to hold an approximation of the velocity of the weights.
For extra computation overhead, the weight prediction mechanisms of XPipe[68] and SpecTrain[59] introduce extra computation overhead. Furthermore, the learning rate rescheduling and discrepancy correction techniques used in PipeMare[66] also require doing extra computation. ZB-H2[56] requires executing extra computation when rollbacking an optimizer step.
In terms of extra communication overhead, the basic communication overhead includes transmitting activation values during forward pass and transmitting gradients during backward propagation. However, it should be noted that Chimera[47] and GEMS[54] require the corresponding stage to perform an AllReduce operation for gradient synchronization in each iteration, which incurs additional communication overhead. The elastic averaging technique in AvgPipe[61] adds communication to maintain weight consistency among multiple pipelines. The interleaved “1F1B” schedule of Megatron-LM[55] reduces the bubble size but also incurs extra communication due to the introduction of chunks. Other pipelined parallel methods do not have this additional communication overhead.
4. Load Balance for Pipeline Training
4.1 Load Balance for Intra-Node Training
When executing pipeline training on a computing node, model partition is one of the key techniques to achieve load balance within a node. The partitioning strategy of pipeline parallelism is to divide the computational graph of a model into multiple consecutive layer blocks (also known as stages), enabling parallel execution of operations within each stage. The objective of the partitioning strategy is to balance the computation across GPUs, fully utilize computational resources, and reduce the bubble overhead. Since the complexity of different DNN layers varies, it would benefit load balance a lot when partitioning the DNN layers in a balanced way. Much prior research has been focused on addressing this issue. The most important technique to achieve optimal partitioning of a DNN model is dynamic programming which is successfully used in PipeDream[28], PipeDream-2BW[58], EffTra[69], and DAPPLE[48]. Another technique for model partition is reinforcement learning[49]. Moreover, Alpa[70] discovers that the hierarchical search method can effectively search for model partitioning strategies, thereby contributing to load balance for intra-node training. AutoPipe[71] contains a planner for automatically generating a balanced pipeline partition scheme with a heuristic partition search algorithm. Unity[72] defines a set of rules for computational subgraph substitution based on computational optimization techniques. Furthermore, vPipe[73] designs a live layer migration protocol that mitigates layers from intense stages to their adjacent stages to achieve more balanced partitions with higher throughput.
Other important techniques mainly focus on reducing the pipeline bubbles or filling them with computations, ultimately promoting computational load balance among GPUs. The related technologies include the followings.
1) Microbatching, which achieves the balance of computation by hiding pipeline bubbles. With this technique, a mini-batch of training data is split into micro-batches with smaller sizes. The pipelining of these micro-batches in a mini-batch reduces the number of bubbles in the pipeline, contributing to a better load balance across GPUs.
2) The “1F1B” schedule, which is widely used in asynchronous pipeline approaches such as PipeDream[28], PipeDream-2BW[58], WPipe[62], and XPipe[68]. By letting all mini-batches/micro-batches be scheduled in a one-forward-one-backward manner, the “1F1B” schedule almost generates no bubble overhead, makes each GPU busy training the stages at any pipeline time unit, and contributes a lot to the load balance across GPUs.
3) Dual-/multiple-pipeline training, which is frequently used to achieve load balance on a multi-GPU computing node. The key insight of this technique is to combine two or more pipelines to reduce the number of bubbles and thus achieve more balanced pipelined training. Typical cases include Chimera[47] and AvgPipe[61]. However, one should note that this technique usually incurs extra storage overhead for storing weights and extra communication overhead for realizing weight synchronization.
4) Bubble filling, which suggests that the pipeline bubbles can be filled with computations. A typical example is PipeFisher[74] which fills the pipeline bubbles with the work of K-FAC, a second-order optimization based on the Fisher information matrix, to gain auxiliary convergence benefits in large language models (LLMs) training.
4.2 Load Balance for Inter-Node Training
Distributed deep learning always requires distributing the training process across multiple nodes or devices to speed up the training process. In a distributed setting, the intra-node communication bandwidth is usually larger than that of the inter-node. It requires a load balance training strategy to tackle this imbalance. Load balance for inter-node training is pivotal to scale pipeline parallelism training among the distributed nodes and thus maximize efficiency and speed up the training process.
Hybrid parallelism is the most frequently used technique to achieve load balance for pipeline training. By harnessing the advantages offered by different parallel training modes, hybrid parallelism strives to achieve enhanced efficiency and scalability in model training. In particular, the mixture of pipeline parallelism and data parallelism is widely used to scale pipeline parallelism to multi-machine-multi-GPU computing systems. Popular pipeline approaches such as GPipe[29], PipeDream[28], PipeDream-2BW[58], DAPPLE[48], and GEMS[54] show improved performance and scalability when using this hybrid parallelism strategy. Another hybrid training way to achieve load balance across multiple computing nodes is combining pipeline parallelism with both data parallelism and tensor parallelism. The representative cases include DistBelief[24], Piper[75], and Megatron-LM[20] which efficiently train large-scale language models on GPU clusters. On the other hand, PMP has been demonstrated to perform well in utilizing cross-server connections with a large-scale number of GPUs[20, 70]. When employing PMP for inter-node training while using TMP for intra-node training (e.g., 3D parallelism), the layer partition techniques described in Subsection 4.1 can be easily applied to achieve inter-node load balance. In this case, the model partition techniques for TMP come as the main technique to achieve intra-layer load balance. We do not elaborate on the model partition techniques[20] for TMP as these go beyond the scope of this paper.
5. Optimization of Computation, Storage, and Communication
In this section, we focus on computation, storage, and communication, and discuss the main techniques to improve the performance of pipeline training.
5.1 Optimization of Computation
The optimization of computation refers to decreasing the computation cost and avoiding unnecessary and intensive computations. To attain high performance, Megatron-LM[20] employs model-specific optimizations to the computation graph. These optimizations include changing the data layout in the transformer layer, generating fused kernels for a sequence of element-wise operations, and creating two custom kernels to enable the fusion of scale, mask, and softmax (reduction) operations. PipeFB[76] proposes to execute the computations of forward passes and backward propagations with different GPUs to accelerate pipeline training. XPipe[60] achieves the optimization of computation by avoiding repetitive weight prediction. To be concrete, for each mini-batch training, XPipe designates the first micro-batch as a bellwether and lets it be in charge of doing weight prediction ahead of both the forward pass and backward propagation. At the same time, the other micro-batches in the same mini-batch directly make use of the predicted weights by the bellwether to do both forward pass and backward propagation, leading to much less computational cost compared with making all micro-batches repeatedly execute weight predictions.
5.2 Optimization of Storage
The recomputation (also known as checkpointing)[77] technique is always leveraged to minimize activation memory usage and has been adopted by many popular PMP approaches such as GPipe, PipeDream, and DAPPLE. By leveraging this technique, each GPU only needs to store output activations at the partition boundaries and recompute the forward pass during the backward propagation, avoiding storing the activations of all intermediate layers within the partition. Furthermore, the optimization of storage also involves achieving a balanced memory consumption across GPUs. A successful example is BPipe[78] which transfers intermediate activations between GPUs to enable all GPUs to utilize comparable amounts of memory. It is worth noting that the optimization of storage does not come for free, always at the cost of increasing the computation or communication cost. For example, recomputation incurs more forward pass computation, and transferring intermediate activations leads to extra communication costs. Other efforts are dedicated to making use of the CPU memory. For instance, vPipe[73] utilizes a hybrid combination of swap and recomputation of activation tensors which asynchronously transfers activations to CPU memory and gets them back to GPU memory for recomputing the forward pass ahead of the backward propagation. SuperNeurons[79] adopts offloading and prefetching techniques to address the challenge of limited GPU resident memory. Similar techniques on storage optimization include using real-time data transferring[80, 76], where the activations are offloaded to the CPU and other GPUs with free memory to reduce the peak memory usage of PipeDream. Additionally, MPress[81] proposes a method that utilizes spare GPU memory to accelerate training by combining recomputation and swap methods. Furthermore, the Zero Redundancy Optimizer (ZeRO) optimizer[45], a technique to optimize memory, can be integrated with 3D parallelism to achieve the goal of optimization of storage when training LLMs with 3D parallelism[82].
5.3 Optimization of Communication
The main approach for communication optimization is overlapping[28], which generally refers to the overlapping of computation and communication. For the PMP mode, this technique usually refers to the overlapping of communication with the computation of a subsequent mini-batch/micro-batch. The premise of using overlapping is that the computation and communication are completely independent and operate on different tensor data. The overlapping technique is widely used in asynchronous pipeline approaches such as PipeDream[28], PipeDream-2BW[20], and XPipe[68], in which, by using the overlapping of computation and the communication of activations or gradients, each GPU is allowed to proceed with the next input mini-batch before receiving the activations or gradients from the previous mini-batch. In addition, GEMS[54] and Chimera[47] also leverage the overlapping technique to hide the gradient synchronization between the bidirectional pipelines. Furthermore, other communication optimizations focus on decreasing the communication redundancy, e.g., the Scatter/Gather communication optimization in Megatron-LM[55].
6. Discussion
PMP has been acting as one of the most important approaches to training “big models” due to its low communication overhead and high efficiency. The efficient PMP approach not only pursues rapid iteration but also needs to ensure the effectiveness of parameter learning. One should strive to achieve a good tradeoff among computation, storage, and communication to maximize the performance of the PMP approach. At the same time, consideration should also be given to designing corresponding pipeline parallel training methods according to the characteristics of computer architecture to fully utilize its computing power. For future research in pipeline parallelism, we suggest two potential directions that hold significant importance.
6.1 Asynchronous Pipeline Parallelism with Effective Parameter Learning
Asynchronous pipeline parallelism approaches always achieve high GPU utilization and demonstrate pretty good concurrency, but their convergence properties are often inferior to synchronous approaches. Designing efficient asynchronous PMP approaches requires striking the optimal balance between concurrency and learning efficiency. As mentioned before, weight inconsistency and weight staleness issues are the significant flaws in asynchronous pipeline parallelism with the “1F1B” schedule that result in ineffective parameter learning. The weight stashing technique[28, 58] can only address the weight inconsistency problem, leaving the weight staleness issue unsolved. On the other hand, the performance of existing weight prediction based approaches such as SpecTrain[59] and XPipe[60] heavily rely on the update rule of the used optimizer, despite that using the weight prediction technique can simultaneously alleviate the weight inconsistency and weight staleness issues. How to simultaneously and effectively address the weight inconsistency and staleness issues still remains an unsolved challenge.
Very recently, Guan et al.[83, 84] restudied the weight prediction and successfully applied it to boost the convergence of DNN training when using popular optimizers such as momentum SGD, RMSprop[85], Adam[65], and AdamW[86]. Especially, the proposed XGrad[84] framework illustrates that weight prediction can boost all the commonly-used gradient-based optimizers, including SGD with momentum, RMSprop, Adam, AdamW, AdaBelief[87], and AdaM3[88]. Therefore, in future research on asynchronous pipelined training, we forecast that dynamically predicting weights based on the used optimizer is a promising way to improve the robustness of weight prediction and enhance the training efficiency of asynchronous pipeline parallelism approaches.
6.2 Pipeline Parallelism for Large-Scale Heterogeneous Computing Platforms
Currently, high-performance computing platforms, represented by supercomputers, provide powerful computational capabilities for deep learning. Supercomputers commonly employ heterogeneous computing architectures, combining CPUs with accelerators such as GPUs, MICs, and FPGAs. For example, the Tianhe-2 supercomputer[89] adopts a CPU+MIC heterogeneous parallel architecture, while the Tianhe-1A supercomputer[90] utilizes a CPU+GPU heterogeneous parallel architecture. Existing distributed pipeline parallel training systems, such as PipeDream[28], PipeDream-2BW[58], and DAPPLE[48], typically employ a hybrid parallel training mode that combines pipeline parallelism and data parallelism. These pipeline parallelism training systems always assume homogeneous computing platforms for pipeline parallel training. Furthermore, existing heterogeneous pipeline parallel training methods, such as Pipe-Torch[91] and HetPipe[92], are not suitable for CPU+GPU/MIC heterogeneous computing platforms. These approaches maintain the same limitations, as they do not fully exploit the computational power and storage capacity of CPUs on each node in large-scale GPU clusters, thus failing to fully harness the parallel computing capability of supercomputers based on heterogeneous computing architectures. Therefore, in future research, investigating pipeline parallel training systems specifically designed for CPU+GPU/MIC heterogeneous computing platforms holds significant potential and value in terms of research significance and practical applications.
7. Conclusions
As a pretty promising approach, the pipeline model parallelism (PMP) mode is believed to play a more important role in addressing the challenge of “big models”. This paper presented a comprehensive survey of the state-of-the-art approaches for PMP, including the basic concepts and main challenges, the manner of pipeline scheduling, and the main techniques to achieve intra-node and inter-node load balance. Furthermore, it covers the main techniques to optimize computation, storage, and communication—essential factors influencing the performance of pipelined training. Additionally, potential research directions are discussed.
Although research on pipeline parallelism has made significant progress, we believe there is still room for improvement in pipeline parallel training, especially in overcoming GPU memory bottlenecks to further enhance training efficiency.
Acknowledgements: Lei Guan thanks Prof. Shi-Gang Li at Beijing University of Posts and Telecommunications (BUPT) for stimulating discussions about pipeline parallelism. -
Table 1 Descriptions of Notations Used in Subsection 3.3
Symbol Description D Number of pipeline stages (pipeline depth) P Number of replicated pipelines B Micro-batch size T Number of micro-batches in each mini-batch N Mini-batch size (N=T\times B) M_{\boldsymbol{\theta}} Memory consumption for weights of a stage M_a Memory consumption for activations of a stage Table 2 Summary of Framework, Data Unit, and Schedule Manner of Typical Pipeline Parallelism Approaches
Approach Framework Data Unit Schedule GPipe[29] TensorFlow Micro-batch Synchronous GEMS[54] TensorFlow Micro-batch Synchronous DAPPLE[48] TensorFlow Micro-batch Synchronous Chimera[47] PyTorch Micro-batch Synchronous Megatron-LM[55] PyTorch Micro-batch Synchronous ZB-H2[56] PyTorch Micro-batch Synchronous AMPNet[57] TensorFlow Mini-batch Asynchronous PipeDream[28] PyTorch Mini-batch Asynchronous XPipe[60] PyTorch Micro-batch Asynchronous SpecTrain[59] PyTorch Mini-batch Asynchronous PipeDream-2BW[58] PyTorch Micro-batch Asynchronous PipeMare[66] PyTorch Micro-batch Asynchronous AvgPipe[61] PyTorch Micro-batch Asynchronous WPipe[62] PyTorch Micro-batch Asynchronous Table 3 Comparisons of Typical PMP Approaches
Approach Bubble Ratio Convergence Weights Memory Activations Memory Extra Mem., Comp., and Comm.^\sharp GPipe (D-1)/(T+D-1) * Excellent M_{\boldsymbol{\theta}} T \times M_a [×, ×, ×] GEMS \approx (D-1)/(D+{1}/{2}) * Excellent 2 M_{\boldsymbol{\theta}} M_a [√, ×, √] DAPPLE (D-1)/(D+T-1) * Excellent M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [×, ×, ×] Chimera (D-2)/(2T+D-2) * Excellent 2 M_{\boldsymbol{\theta}} [ (D/2+1)M_a , D\times M_a ]* [√, ×, √] Megatron-LM (D-1) / (v\times T) ♢ Excellent M_{\boldsymbol{\theta}} T\times M_a [×, ×, √] ZB-H2 ≈ 0% Excellent M_{\boldsymbol{\theta}} (2D-1)\times {M_a} ^\S [×, √, ×] AMPNet ≈ 0% Poor M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [×, ×, ×] PipeDream ≈ 0% Good [ M_{\boldsymbol{\theta}} , D \times M_{\boldsymbol{\theta}} ] [ M_a , D\times M_a ] [√, ×, ×] XPipe ≈ 0% Good† M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, √, ×] SpecTrain ≈ 0% Good‡ M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, √, ×] PipeDream-2BW ≈ 0% Good 2M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, ×, ×] PipeMare ≈ 0% Good M_{\boldsymbol{\theta}} [ M_a , D\times M_a ] [√, √, ×] AvgPipe ≈ 0% Good P \times M_{\boldsymbol{\theta}} [1, D \times T]\times P\times M_a [√, ×, √] WPipe ≈ 0% Good 2M_{\boldsymbol{\theta}} T\times M_a [√, ×, ×] Note: *: concluded by [47]; ♢: concluded by [55], where v denotes the number of chunks on each GPU; †: does not cover all optimizers; ‡: only works well when using momentum SGD as the optimizer; \S : peak activations memory concluded by [56]; \sharp : [√, ×, √] means requiring extra memory consumption and communication but no extra computation, and vice versa. -
[1] He K M, Zhang X Y, Ren S Q, Sun J. Deep residual learning for image recognition. In Proc. the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2016, pp.770–778. DOI: 10.1109/CVPR.2016.90.
[2] Karpathy A, Toderici G, Shetty S, Leung T, Sukthankar R, Fei-Fei L. Large-scale video classification with convolutional neural networks. In Proc. the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2014, pp.1725–1732. DOI: 10.1109/CVPR.2014.223.
[3] Hinton G, Deng L, Yu D, Dahl G E, Mohamed A R, Jaitly N, Senior A, Vanhoucke V, Nguyen P, Sainath T N, Kingsbury B. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 2012, 29(6): 82–97. DOI: 10.1109/MSP.2012.2205597.
[4] Li J Y. Recent advances in end-to-end automatic speech recognition. APSIPA Trans. Signal and Information Processing, 2022, 11(1): e8. DOI: 10.1561/116.00000050.
[5] Wu Y, Schuster M, Chen Z F et al. Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv: 1609.08144, 2016. https://arxiv.org/abs/1609.08144, May 2024.
[6] Dabre R, Chu C H, Kunchukuttan A. A survey of multilingual neural machine translation. ACM Computing Surveys, 2021, 53(5): Article No. 99. DOI: 10.1145/3406095.
[7] Chen C Y, Seff A, Kornhauser A, Xiao J X. DeepDriving: Learning affordance for direct perception in autonomous driving. In Proc. the 2015 IEEE International Conference on Computer Vision, Dec. 2015, pp.2722–2730. DOI: 10.1109/ICCV.2015.312.
[8] Bojarski M, Del Testa D, Dworakowski D et al. End to end learning for self-driving cars. arXiv: 1604.07316, 2016. https://arxiv.org/abs/1604.07316, May 2024.
[9] Real E, Aggarwal A, Huang Y P, Le Q V. Regularized evolution for image classifier architecture search. In Proc. the 33rd AAAI Conference on Artificial Intelligence, Jan. 27–Feb. 1, 2019, pp.4780–4789. DOI: 10.1609/aaai.v33i01.33014780.
[10] Devlin J, Chang M W, Lee K, Toutanova K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proc. the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Jun. 2019, pp.4171–4186. DOI: 10.18653/V1/N19-1423.
[11] Radford A, Wu J, Child R, Luan D, Amodei D, Sutskever I. Language models are unsupervised multitask learners. OpenAI Blog, 2019, 1(8): 9.
[12] Brown T B, Mann B, Ryder N et al. Language models are few-shot learners. arXiv: 2005.14165, 2020. https://arxiv.org/abs/2005.14165, May 2024.
[13] Fedus W, Zoph B, Shazeer N. Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. The Journal of Machine Learning Research, 2022, 23(1): 120.
[14] Chen M, Radford A, Child R, Wu J, Jun H, Luan D, Sutskever I. Generative pretraining from pixels. In Proc. the 37th International Conference on Machine Learning, Jul. 2020, Article No. 158.
[15] Zeng W, Ren X Z, Su T et al. PanGu-α: Largescale autoregressive pretrained Chinese language models with auto-parallel computation. arXiv: 2104.12369, 2021. https://arxiv.org/abs/2104.12369, May 2024.
[16] Wang S H, Sun Y, Xiang Y et al. ERNIE 3.0 titan: Exploring larger-scale knowledge enhanced pre-training for language understanding and generation. arXiv: 2112.12731, 2021. https://arxiv.org/abs/2112.12731, May 2024.
[17] Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A N, Kaiser Ł, Polosukhin I. Attention is all you need. In Proc. the 31st International Conference on Neural Information Processing Systems, Dec. 2017, pp.6000–6010.
[18] Deng J, Dong W, Socher R, Li L J, Li K, Fei-Fei L. ImageNet: A large-scale hierarchical image database. In Proc. the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Jun. 2009, pp.248–255. DOI: 10.1109/CVPR.2009.5206848.
[19] Abu-El-Haija S, Kothari N, Lee J, Natsev P, Toderici G, Varadarajan B, Vijayanarasimhan S. YouTube-8M: A large-scale video classification benchmark. arXiv: 1609.08675, 2016. https://arxiv.org/abs/1609.08675, May 2024.
[20] Narayanan D, Shoeybi M, Casper J et al. Efficient large-scale language model training on GPU clusters using megatron-LM. In Proc. the 2021 International Conference for High Performance Computing, Networking, Storage and Analysis, Nov. 2021, Article No. 58. DOI: 10.1145/3458817.3476209.
[21] Goyal P, Dollár P, Girshick R, Noordhuis P, Wesolowski L, Kyrola A, Tulloch A, Jia Y Q, He K M. Accurate, large minibatch SGD: Training ImageNet in 1 hour. arXiv: 1706.02677, 2017. https://arxiv.org/abs/1706.02677, May 2024.
[22] You Y, Gitman I, Ginsburg B. Scaling SGD batch size to 32k for ImageNet training. arXiv: 1708.03888, 2017. https://arxiv.org/abs/1708.03888v1?2, May 2024.
[23] Assran M, Loizou N, Ballas N, Rabbat M. Stochastic gradient push for distributed deep learning. In Proc. the 36th International Conference on Machine Learning, Jun. 2019, pp.344–353.
[24] Dean J, Corrado G S, Monga R et al. Large scale distributed deep networks. In Proc. the 25th International Conference on Neural Information Processing Systems, Dec. 2012, pp.1223–1231.
[25] Shazeer N, Cheng Y L, Parmar N et al. Mesh-TensorFlow: Deep learning for supercomputers. In Proc. the 32nd International Conference on Neural Information Processing Systems, Dec. 2018, pp.10435–10444.
[26] Jia Z H, Zaharia M, Aiken A. Beyond data and model parallelism for deep neural networks. In Proc. the 2019 SysML Conference, Mar. 31–Apr. 2, Apr. 2019, pp.1–13.
[27] Gan W S, Lin J C W, Fournier-Viger P, Chao H C, Yu P S. A survey of parallel sequential pattern mining. ACM Trans. Knowledge Discovery from Data, 2019, 13(3): 25. DOI: 10.1145/3314107.
[28] Narayanan D, Harlap A, Phanishayee A, Seshadri V, Devanur N R, Ganger G R, Gibbons P B, Zaharia M. PipeDream: Generalized pipeline parallelism for DNN training. In Proc. the 27th ACM Symposium on Operating Systems Principles, Oct. 2019, pp.1–15. DOI: 10.1145/3341301.3359646.
[29] Huang Y P, Cheng Y L, Bapna A, Firat O, Chen M X, Chen D H, Lee H, Ngiam J, Le Q V, Wu Y H, Chen Z F. GPipe: Efficient training of giant neural networks using pipeline parallelism. In Proc. the 33rd International Conference on Neural Information Processing Systems, Dec. 2019, Article No. 10.
[30] Pouyanfar S, Sadiq S, Yan Y L, Tian H M, Tao Y D, Reyes M P, Shyu M L, Chen S C, Iyengar S S. A survey on deep learning: Algorithms, techniques, and applications. ACM Computing Surveys, 2019, 51(5): 92. DOI: 10.1145/3234150.
[31] Ben-Nun T, Hoefler T. Demystifying parallel and distributed deep learning: An in-depth concurrency analysis. ACM Computing Surveys, 2020, 52(4): 65. DOI: 10.1145/3320060.
[32] Tang Z H, Shi S H, Wang W, Li B, Chu X W. Communication-efficient distributed deep learning: A comprehensive survey. arXiv: 2003.06307, 2020. https://arxiv.org/abs/2003.06307, May 2024.
[33] Mayer R, Jacobsen H A. Scalable deep learning on distributed infrastructures: Challenges, techniques, and tools. ACM Computing Surveys, 2021, 53(1): Article No. 3. DOI: 10.1145/3363554.
[34] Liang P, Tang Y, Zhang X D, Bai Y H, Su T, Lai Z Q, Qiao L B, Li D S. A survey on auto-parallelism of large-scale deep learning training. IEEE Trans. Parallel and Distributed Systems, 2023, 34(8): 2377–2390. DOI: 10.1109/TPDS.2023.3281931.
[35] Shen L, Sun Y, Yu Z Y, Ding L, Tian X M, Tao D C. On efficient training of large-scale deep learning models: A literature review. arXiv: 2304.03589, 2023. https://arxiv.org/abs/2304.03589, May 2024.
[36] Kumar S. Introduction to Parallel Programming. Cambridge University Press, 2022.
[37] Abadi M, Barham P, Chen J N et al. TensorFlow: A system for large-scale machine learning. In Proc. the 12th USENIX Conference on Operating Systems Design and Implementation, Nov. 2016, pp.265–283.
[38] Paszke A, Gross S, Massa F et al. PyTorch: An imperative style, high-performance deep learning library. In Proc. the 33rd Conference on Neural Information Processing Systems, Dec. 2019, Article No. 721.
[39] Sergeev A, Del Balso M. Horovod: Fast and easy distributed deep learning in TensorFlow. arXiv: 1802.05799, 2018. https://arxiv.org/abs/1802.05799, May 2024.
[40] Li M, G. Andersen D G, Park J W, Smola A J, Ahmed A, Josifovski V, Long J, Shekita E J, Su B Y. Scaling distributed machine learning with the parameter server. In Proc. the 11th USENIX Conference on Operating Systems Design and Implementation, Oct. 2014, pp.583–598.
[41] Cui H G, Zhang H, Ganger G R, Gibbons P B, Xing E P. GeePs: Scalable deep learning on distributed GPUs with a GPU-specialized parameter server. In Proc. the 11th European Conference on Computer Systems, Apr. 2016, Article No. 4. DOI: 10.1145/2901318.2901323.
[42] Patarasuk P, Yuan X. Bandwidth optimal all-reduce algorithms for clusters of workstations. Journal of Parallel and Distributed Computing, 2009, 69(2): 117–124. DOI: 10.1016/j.jpdc.2008.09.002.
[43] Alistarh D, Grubic D, Li J Z, Tomioka R, Vojnovic M. QSGD: Communication-efficient SGD via gradient quantization and encoding. In Proc. the 31st International Conference on Neural Information Processing Systems, Dec. 2017, pp.1707–1718.
[44] Jia Z H, Lin S N, Qi C R, Aiken A. Exploring hidden dimensions in parallelizing convolutional neural networks. In Proc. the 35th International Conference on Machine Learning, Jul. 2018, pp.2279–2288.
[45] Rajbhandari S, Rasley J, Ruwase O, He Y X. ZeRO: Memory optimizations toward training trillion parameter models. In Proc. the 2020 International Conference for High Performance Computing, Networking, Storage and Analysis, Nov. 2020. DOI: 10.1109/SC41405.2020.00024.
[46] Gusak J, Cherniuk D, Shilova A et al. Survey on efficient training of large neural networks. In Proc. the 31st International Joint Conference on Artificial Intelligence, Jul. 2022, pp.5494–5501. DOI: 10.24963/ijcai.2022/769.
[47] Li S G, Hoefler T. Chimera: Efficiently training large-scale neural networks with bidirectional pipelines. In Proc. the 2021 International Conference for High Performance Computing, Networking, Storage and Analysis, Nov. 2021, Article No. 27. DOI: 10.1145/3458817.3476145.
[48] Fan S Q, Rong Y, Meng C et al. DAPPLE: A pipelined data parallel approach for training large models. In Proc. the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Feb. 2021, pp.431–445. DOI: 10.1145/3437801.3441593.
[49] Mirhoseini A, Pham H, Le Q V, Steiner B, Larsen R, Zhou Y F, Kumar N, Norouzi M, Bengio S, Dean J. Device placement optimization with reinforcement learning. In Proc. the 34th International Conference on Machine Learning, Aug. 2017, pp.2430–2439.
[50] Krizhevsky A. One weird trick for parallelizing convolutional neural networks. arXiv: 1404.5997, 2014. https://arxiv.org/abs/1404.5997, May 2024.
[51] Li S G, Liu H X, Bian Z D, Fang J R, Huang H C, Liu Y L, Wang B X, You Y. Colossal-AI: A unified deep learning system for large-scale parallel training. In Proc. the 52nd International Conference on Parallel Processing, Aug. 2023, pp.766–775. DOI: 10.1145/3605573.3605613.
[52] Lai Z Q, Li S W, Tang X D, Ge K S, Liu W J, Duan Y B, Qiao L B, Li D S. Merak: An efficient distributed DNN training framework with automated 3D parallelism for giant foundation models. IEEE Trans. Parallel and Distributed Systems, 2023, 34(5): 1466–1478. DOI: 10.1109/TPDS.2023.3247001.
[53] Ramashekar T, Bondhugula U. Automatic data allocation and buffer management for multi-GPU machines. ACM Trans. Architecture and Code Optimization, 2013, 10(4): 60. DOI: 10.1145/2544100.
[54] Jain A, Awan A A, Aljuhani A M, Hashmi J M, Anthony Q G, Subramoni H, Panda D K, Machiraju R, Parwani A. GEMS: GPU-enabled memory-aware model-parallelism system for distributed DNN training. In Proc. the 2020 International Conference for High Performance Computing, Networking, Storage and Analysis, Nov. 2020, pp.1–15. DOI: 10.1109/SC41405.2020.00049.
[55] Shoeybi M, Patwary M, Puri R, LeGresley P, Casper J, Catanzaro B. Megatron-LM: Training multi-billion parameter language models using model parallelism. arXiv: 1909.08053, 2019. https://arxiv.org/abs/1909.08053, May 2024.
[56] Qi P, Wan X, Huang G, Lin M. Zero bubble pipeline parallelism. In Proc. the 11th International Conference on Learning Representations, Jul. 2023.
[57] Gaunt A L, Johnson M A, Riechert M, Tarlow D, Tomioka R, Vytiniotis D, Webster S. AMPNet: Asynchronous model-parallel training for dynamic neural networks. arXiv: 1705.09786, 2017. https://arxiv.org/abs/1705.09786, May 2024.
[58] Narayanan D, Phanishayee A, Shi K Y, Chen X, Zaharia M. Memory-efficient pipeline-parallel DNN training. In Proc. the 38th International Conference on Machine Learning, Jul. 2021, pp.7937–7947.
[59] Chen C C, Yang C L, Cheng H Y. Efficient and robust parallel DNN training through model parallelism on multi-GPU platform. arXiv: 1809.02839, 2018. https://arxiv.org/abs/1809.02839, May 2024.
[60] Guan L, Yin W T, Li D S, Lu X C. XPipe: Efficient pipeline model parallelism for multi-GPU DNN training. arXiv: 1911.04610, 2019. https://arxiv.org/abs/1911.04610, May 2024.
[61] Chen Z H, Xu C, Qian W N, Zhou A Y. Elastic averaging for efficient pipelined DNN training. In Proc. the 28th ACM SIGPLAN Annual Symposium on Principles and Practice of Parallel Programming, Feb. 2023, pp.380–391. DOI: 10.1145/3572848.3577484.
[62] Yang P C, Zhang X M, Zhang W P, Yang M, Wei H. Group-based interleaved pipeline parallelism for large-scale DNN training. In Proc. the 10th International Conference on Learning Representations, Apr. 2022.
[63] Qian N. On the momentum term in gradient descent learning algorithms. Neural Networks, 1999, 12(1): 145–151. DOI: 10.1016/S0893-6080(98)00116-6.
[64] Sutskever I, Martens J, Dahl G, Hinton G. On the importance of initialization and momentum in deep learning. In Proc. the 30th International Conference on Machine Learning, Jun. 2013, pp.III-1139–III-1147.
[65] Kingma D P, Ba J. Adam: A method for stochastic optimization. In Proc. the 3rd International Conference on Learning Representations, May 2015.
[66] Yang B W, Zhang J, Li J, Ré C, Aberger C R, De Sa C. PipeMare: Asynchronous pipeline parallel DNN training. arXiv: 1910.05124, 2019. https://arxiv.org/abs/1910.05124, May 2024.
[67] Zhang S X, Choromanska A, LeCun Y. Deep learning with elastic averaging SGD. In Proc. the 28th International Conference on Neural Information Processing Systems, Dec. 2015, pp.685–693.
[68] Guan L, Qiao L B, Li D S, Sun T, Ge K S, Lu X C. An efficient ADMM-based algorithm to Nonconvex penalized support vector machines. In Proc. the 2018 IEEE International Conference on Data Mining Workshops, Nov. 2018, pp.1209–1216. DOI: 10.1109/ICDMW.2018.00173.
[69] Zeng Z H, Liu C B, Tang Z, Chang W L, Li K L. Training acceleration for deep neural networks: A hybrid parallelization strategy. In Proc. the 58th ACM/IEEE Design Automation Conference, Dec. 2021, pp.1165–1170. DOI: 10.1109/DAC18074.2021.9586300.
[70] Zheng L M, Li Z H, Zhang H, Zhuang Y H, Chen Z F, Huang Y P, Wang Y D, Xu Y Z, Zhuo D Y, Xing E P, Gonzalez J E, Stoica I. Alpa: Automating inter- and Intra-Operator parallelism for distributed deep learning. In Proc. the 16th USENIX Symposium on Operating Systems Design and Implementation, Jul. 2022, pp.559–578.
[71] Liu W J, Lai Z Q, Li S W, Duan Y B, Ge K S, Li D S. AutoPipe: A fast pipeline parallelism approach with balanced partitioning and micro-batch slicing. In Proc. the 2022 IEEE International Conference on Cluster Computing, Sept. 2022, pp.301–312. DOI: 10.1109/CLUSTER51413.2022.00042.
[72] Unger C, Jia Z H, Wu W et al. Unity: Accelerating DNN training through joint optimization of algebraic transformations and parallelization. In Proc. the 16th USENIX Symposium on Operating Systems Design and Implementation, Jul. 2022, pp.267–284.
[73] Zhao S X, Li F X, Chen X S, Guan X X, Jiang J Y, Huang D, Qing Y, Wang S, Wang P, Zhang G, Li C, Luo P, Cui H M. VPipe: A virtualized acceleration system for achieving efficient and scalable pipeline parallel DNN training. IEEE Trans. Parallel and Distributed Systems, 2022, 33(3): 489–506. DOI: 10.1109/TPDS.2021.3094364.
[74] Osawa K, Li S, Hoefler T. Pipefisher: Efficient training of large language models using pipelining and fisher information matrices. In Proc. the 6th Conference on Machine Learning and Systems, May 2023.
[75] Tarnawski J, Narayanan D, Phanishayee A. Piper: Multidimensional planner for DNN parallelization. In Proc. the 35th International Conference on Neural Information Processing Systems, Dec. 2021, Article No. 1902.
[76] Jiang W, Wang B, Ma S, Hou X, Huang L B, Dai Y, Fang J B. PipeFB: An optimized pipeline parallelism scheme to reduce the peak memory usage. In Proc. the 22nd International Conference on Algorithms and Architectures for Parallel Processing, Oct. 2022, pp.590–604. DOI: 10.1007/978-3-031-22677-9_31.
[77] Chen T Q, Xu B, Zhang C Y, Guestrin C. Training deep nets with sublinear memory cost. arXiv: 1604.06174, 2016. https://arxiv.org/abs/1604.06174, May 2024.
[78] Kim T, Kim H, Yu G I, Chun B G. BPIPE: Memory-balanced pipeline parallelism for training large language models. In Proc. the 40th International Conference on Machine Learning, Jul. 2023, Article No. 682.
[79] Wang L N, Ye J M, Zhao Y Y, Wu W, Li A, Song S L, Xu Z L, Kraska T. Superneurons: Dynamic GPU memory management for training deep neural networks. In Proc. the 23rd ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, Feb. 2018, pp.41–53. DOI: 10.1145/3178487.3178491.
[80] Jiang W, Xu R, Ma S, Wang Q, Hou X, Lu H Y. A memory saving mechanism based on data transferring for pipeline parallelism. In Proc. the 2021 IEEE International Conference on Parallel & Distributed Processing with Applications, Big Data & Cloud Computing, Sustainable Computing & Communications, Social Computing & Networking (ISPA/BDCloud/SocialCom/SustainCom), Sept. 30–Oct. 3, 2021, pp.1230–1235. DOI: 10.1109/ISPA-BDCloud-SocialCom-SustainCom52081.2021.00169.
[81] Zhou Q, Wang H Q, Yu X Y, Li C, Bai Y H, Yan F, Xu Y L. MPress: Democratizing billion-scale model training on multi-gpu servers via memory-saving inter-operator parallelism. In Proc. the 29th IEEE International Symposium on High-Performance Computer Architecture, Feb. 25–Mar. 1, 2023, pp.556–569. DOI: 10.1109/HPCA56546.2023.10071077.
[82] Le Scao T, Fan A, Akiki C et al. BLOOM: A 176B-parameter open-access multilingual language model. arXiv: 2211.05100, 2022. https://arxiv.org/abs/2211.05100, May 2024.
[83] Guan L. Weight prediction boosts the convergence of AdamW. In Proc. the 27th Pacific-Asia Conference on Knowledge Discovery and Data Mining, May 2023, pp.329–340. DOI: 10.1007/978-3-031-33374-3_26.
[84] Guan L, Li D S, Shi Y Q, Meng J. XGrad: Boosting gradient-based optimizers with weight prediction. IEEE Trans. Pattern Analysis and Machine Intelligence. DOI: 10.1109/TPAMI.2024.3387399.
[85] Shi N C, Li D W, Hong M Y, Sun R Y. RMSprop converges with proper hyper-parameter. In Proc. the ICLR 2021, May 2021.
[86] Loshchilov I, Hutter F. Decoupled weight decay regularization. arXiv: 1711.05101, 2017. https://arxiv.org/abs/1711.05101, May 2024.
[87] Zhuang J T, Tang T, Ding Y F et al. Adabelief optimizer: Adapting stepsizes by the belief in observed gradients. In Proc. the 34th International Conference on Neural Information Processing Systems, Dec. 2020, pp.18795–18806.
[88] Wang Y Z, Kang Y, Qin C, Wang H, Xu Y, Zhang Y L, Fu Y. Momentum is all you need for data-driven adaptive optimization. In Proc. the 23rd IEEE International Conference on Data Mining, Dec. 2023, pp.1385–1390. DOI: 10.1109/ICDM58522.2023.00179.
[89] Liao X K, Pang Z B, Wang K F, Lu Y T, Xie M, Xia J, Dong D Z, Suo G. High performance interconnect network for Tianhe system. Journal of Computer Science and Technology, 2015, 30(2): 259–272. DOI: 10.1007/s11390-015-1520-7.
[90] Yang X J, Liao X K, Lu K, Hu Q F, Song J Q, Su J S. The TianHe-1A supercomputer: Its hardware and software. Journal of Computer Science and Technology, 2011, 26(3): 344–351. DOI: 10.1007/s02011-011-1137-8.
[91] Zhan J, Zhang J H. Pipe-torch: Pipeline-based distributed deep learning in a GPU cluster with heterogeneous networking. In Proc. the 7th International Conference on Advanced Cloud and Big Data, Sept. 2019, pp.55–60. DOI: 10.1109/CBD.2019.00020.
[92] Park J H, Yun G, Yi C M, Nguyen N T, Lee S, Choi J, Noh S H, Choi Y R. HetPipe: Enabling large DNN training on (whimpy) heterogeneous GPU clusters through integration of pipelined model parallelism and data parallelism. In Proc. the 2020 USENIX Conference on Usenix Annual Technical Conference, Jul. 2020, Article No. 21.
-
期刊类型引用(6)
1. Lei Guan, Dongsheng Li, Yongle Chen, et al. PipeOptim: Ensuring Effective 1F1B Schedule With Optimizer-Dependent Weight Prediction. IEEE Transactions on Knowledge and Data Engineering, 2025, 37(5): 2831.  必应学术
必应学术
2. Cibin Ki, Ramah Sivakumar, Jaison Mulerikkal, et al. A comprehensive survey of machine learning and deep learning approaches for anomaly detection in high-performance computing systems. The Journal of Supercomputing, 2025, 81(8)  必应学术
必应学术
3. Liah Rosenfeld, Leonardo Vanneschi. A survey on batch training in genetic programming. Genetic Programming and Evolvable Machines, 2025, 26(1)  必应学术
必应学术
4. Pinxue Zhao, Hailin Zhang, Fangcheng Fu, et al. MEMO: Fine-grained Tensor Management For Ultra-long Context LLM Training. Proceedings of the ACM on Management of Data, 2025, 3(1): 1.  必应学术
必应学术
5. Yujie Wang, Shiju Wang, Shenhan Zhu, et al. FlexSP: Accelerating Large Language Model Training via Flexible Sequence Parallelism. Proceedings of the 30th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Volume 2,  必应学术
必应学术
6. Lei Guan, Shaofeng Zhang, Yongle Chen. Advances in Energy Recovery and Efficiency Technologies.  必应学术
必应学术
其他类型引用(0)
-
其他相关附件
-
本文附件外链
https://rdcu.be/dODHv -
DOCX格式
Chinese Information 点击下载(43KB) -
PDF格式
2024-3-4-3872-Highlights 点击下载(156KB) -
压缩文件
2024-3-4-3872-Highlights 点击下载(32KB)
-




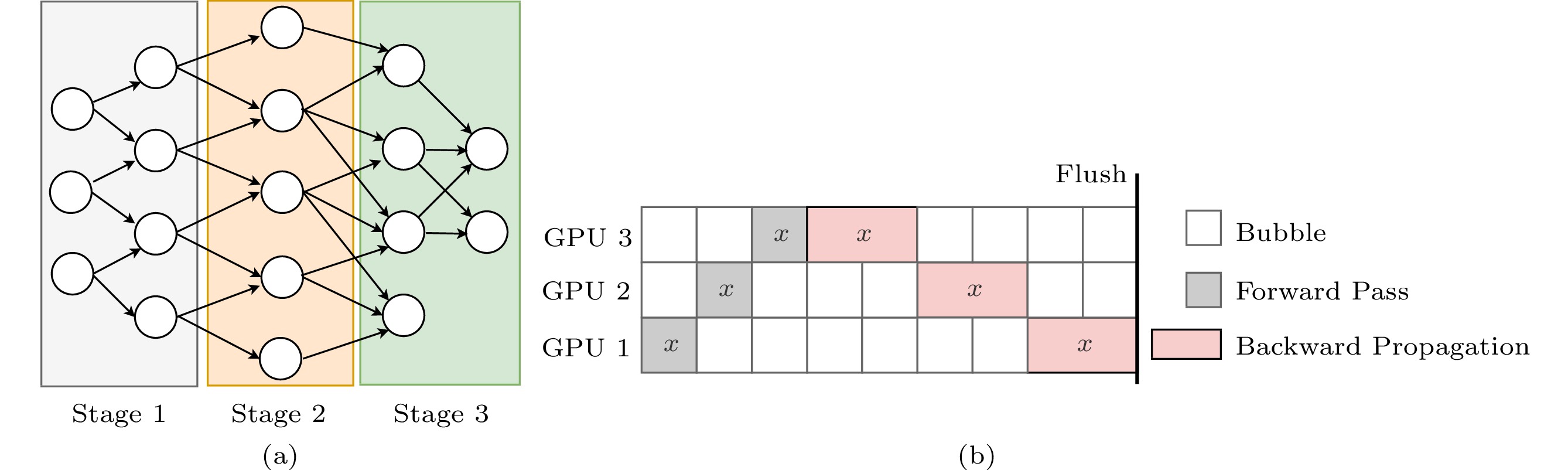
 下载:
下载: