信息年龄敏感的联邦学习
-
摘要:研究背景
联邦学习是一种新兴且有前景的分布式机器学习范式,通过一个中央服务器的协调,促进了全局模型的协同训练,可能涉及大量的客户端。典型的联邦学习过程通常跨足多个轮次,直到达到令人满意的全局模型为止。一方面,联邦学习可以通过在本地保留客户端的训练数据来有效保护客户端的隐私。另一方面,由于只有本地模型参数而不是完整数据集被传输到服务器,联邦学习可以显著减少通信开销。由于这些独特的优势,联邦学习的多个高效且经济有效的工业应用正在涌现。在许多应用场景中,特别是涉及流数据的场景,数据随时间连续生成。参与联邦学习时,客户端有强烈的动机尽可能使用新鲜的数据集来训练其本地模型。因此,客户端将不可避免地在提供新鲜数据集方面花费一些额外的成本,但服务器的总预算通常是有限的。
目的在引入了广泛使用的“信息年龄”(Age-of-Information,AoI)指标来表示数据集的新鲜程度后,我们的研究目标是在信息年龄敏感的联邦学习系统中设计一个客户端选择算法,同时确保服务器的预算不大于预先设定的阈值。
方法我们首先为信息年龄敏感的联邦学习系统推导了一个模型收敛上界。这个上界表明全局模型的损失与本地数据集的新鲜度呈正相关。基于这一洞察,我们将选择最优客户端以最小化全局模型损失的问题转化为一个等价问题:选择具有最小平均AoI值的客户端。随后,我们将此问题构建为一个“无休止多臂赌博机”问题,其中每个客户端被视为一个手臂,客户端的本地数据集的AoI值被视为相应的状态。为了解决这个问题,我们提出了基于Whittle索引的客户端选择算法,称为WICS。其中,我们在每个联邦学习轮次中计算每个客户端的Whittle索引值。基于这些索引值,我们采用贪心策略选择适当的客户端,同时满足服务器端的预算约束。
结果WICS算法实现了服务器可以选择一些客户端提供新鲜数据集进行本地模型训练,以便在预算约束下最小化全局模型的损失。同时,WICS算法可以实现几乎最优的客户端选择性能。
结论全面的理论分析结果表明,本地数据集的高AoI值对全局模型的收敛是有害的。我们观察到,所提出的WICS算法在模型准确性和损失方面的性能均优于比较算法。同时,我们的WICS算法在损失函数为凸或非凸时均能良好运行。此外,我们对所提出算法在更实际场景中的可能扩展进行了各种讨论,然后指出了未来深入研究的潜在方向。
-
关键词:
- 联邦学习 /
- 信息年龄 /
- 无休止多臂赌博机 /
- Whittle索引值算法
Abstract:Federated learning (FL) is an emerging privacy-preserving distributed computing paradigm, enabling numerous clients to collaboratively train machine learning models without the necessity of transmitting clients’ private datasets to the central server. Unlike most existing research where the local datasets of clients are assumed to be unchanged over time throughout the whole FL process, our study addresses such scenarios in this paper where clients’ datasets need to be updated periodically, and the server can incentivize clients to employ as fresh as possible datasets for local model training. Our primary objective is to design a client selection strategy to minimize the loss of the global model for FL loss within a constrained budget. To this end, we introduce the concept of ‘‘Age of Information’’ (AoI) to quantitatively assess the freshness of local datasets and conduct a theoretical analysis of the convergence bound in our AoI-aware FL system. Based on the convergence bound, we further formulate our problem as a restless multi-armed bandit (RMAB) problem. Next, we relax the RMAB problem and apply the Lagrangian Dual approach to decouple it into multiple subproblems. Finally, we propose a Whittle’s Index Based Client Selection (WICS) algorithm to determine the set of selected clients. In addition, comprehensive simulations substantiate that the proposed algorithm can effectively reduce training loss and enhance the learning accuracy compared with some state-of-the-art methods.
-
1. Introduction
Federated learning (FL)[1–5] is an emerging and promising distributed machine learning paradigm, facilitating the collaborative training of a global model by a potentially large number of clients under the coordination of a central server. A typical FL procedure usually spans multiple rounds until a satisfactory global model is achieved[6]. On the one hand, FL can efficiently safeguard clients' data privacy by enabling the retention of their training datasets locally. On the other hand, since only local model parameters rather than complete datasets are transmitted to the server, FL can significantly reduce communication overhead. Owing to these unique advantages, multiple efficient and cost-effective industrial applications of FL are springing up in recent years, such as WeBank employing it for finance and insurance data analysis
1 , Owkin for biomedical data analysis2 , and MELLODDY for drug discovery3 . Meanwhile, considerable research efforts have been directed towards addressing diverse FL issues, including convergence rate optimization[7, 8], accuracy enhancement[9, 10], privacy protection[11–13], and resource allocation[14–17].In general, most existing work assumes that each client possesses a pre-existing dataset and will consistently employ this dataset for local model training during the whole FL process. Nevertheless, in many real-world scenarios, particularly those involving streaming data, the data is continuously generated along with the time. When participating in FL, there is a strong incentive for clients to utilize as fresh datasets as possible to train their local models. This preference is rooted in the belief that fresh data provides a more accurate characterization of model parameters. For instance, a server orchestrates multiple clients to collaboratively train an object identification model via FL, e.g., recognizing formulas on literature and identifying traffic signs on photos, where clients may employ crowdsourcing techniques to periodically recruit mobile users for generating labeled datasets. Naturally, the fresher the labeled datasets, the more effort needed to be devoted to the data labelling, and thus the labeled datasets will be more precise. In such FL scenarios, clients will inevitably spend some extra costs in providing fresh datasets, but the total budget from the server is generally limited. Consequently, a pivotal problem that needs to be dealt with is how to select suitable clients in each round under the limited budget while enabling the server to minimize the loss of the global model.
In this paper, we introduce the well-known “Age of Information” (AoI)[18] metric to indicate the freshness of datasets, which is defined as the elapsed time of data from being collected to being trained for updating local models by clients. The smaller the AoI value of a dataset, the fresher the corresponding data, and thus the more precise the trained local models. Accordingly, the above-mentioned problem is actually instantiated as determining a client selection strategy to minimize the loss of the global model under a given budget, while considering the AoI values of the datasets. Unlike most traditional optimal selection issues with budget constraints, such an AoI-aware problem has two special challenges as follows. Firstly, although the server can reduce the loss of a global model by selecting some clients in each round to update their local datasets and reduce the AoI values, there is no obvious quantitative relationship between the loss of the global model and the decrease of the AoI values of clients' datasets. Secondly, the AoI value of each client's dataset will increase along with the rounds of local training and will return to zero until it is selected to update its own dataset. This indicates that the client selection process and the corresponding AoI values are not independent with each other across different rounds of FL. Both make the client selection problem much more challenging, especially under the budget constraint.
To tackle the above challenges, we first derive a convergence upper bound for the novel AoI-aware FL system. This upper bound shows that the loss of the global model is positively correlated to the freshness of local datasets, i.e., the high AoI values of local datasets will be detrimental to the convergence of the global model. Building upon this insight, we transform the problem of selecting the optimal clients to minimize global model loss into an equivalent problem: selecting clients with the minimum average AoI value. Subsequently, we formulate this problem as a restless multi-armed bandit (RMAB) problem, wherein each client is regarded as an arm, and the AoI values of clients' local datasets are seen as the corresponding state. In order to solve this RMAB problem, we propose the Whittle's Index Based Client Selection (WICS) algorithm. In WICS, we calculate the Whittle's index for each client during each FL round. Based on these indexes, we employ a greedy strategy to pick out appropriate clients while ensuring that the budget of the server is no larger than the prefixed threshold. In a nutshell, our major contributions can be summarized as follows.
∙ We introduce a novel AoI-aware FL system, where the server can select some clients to provide fresh datasets for local model training so as to minimize the loss of the global model under a budget constraint. To the best of our knowledge, this is the first FL work that takes into account the freshness of local datasets for client selection.
∙ We derive a convergence upper bound for the AoI-aware FL system, whereby we analyze the relationship between the training loss of the global model and the AoI values of clients' local datasets. Based on the analysis, we model the client selection problem as an RMAB problem to be solved.
∙ We deduct the RMAB problem into a decoupled model and theoretically derive the optimal strategy for each client, based on which we propose the WICS algorithm by leveraging the Whittle's index methodology. Moreover, we provide a rigorous bound of approximate optimality.
∙ We conduct extensive simulations to verify the performance of WICS based on two real-world datasets and various machine learning models. The results corroborate that the performance of WICS is better than some baselines.
This paper is an extended version of our conference paper[19]. They mainly differ in the following aspects. 1) In this paper, we re-conduct a comprehensive theoretical analysis for WICS, in which we derive a more rigorous and tight bound of approximate optimality. 2) In order to improve client selection efficiency, we update the algorithm process of WICS and provide a more detailed example. 3) We add various discussions on possible extensions of WICS for more practical scenarios. Meanwhile, we point out the potential directions for future in-depth research. 4) We carry out more sufficient experiments with the support vector machines model, which can demonstrate the significant performance of WICS for more practical applications.
The remainder of the paper is organized as follows. In Section 2, we introduce our model and problem. Then, we carry on the convergence analysis in Section 3. The WICS algorithm is elaborated in Section 4. Next, we evaluate the performance of WICS in Section 5. After reviewing related work in Section 6, we make a discussion on the potential directions in Section 7. Finally, we conclude the paper. For ease of presentation, all proofs are moved to the Appendix
4 .2. System Overview and Problem Formulation
2.1 Federated Learning with Data Collection
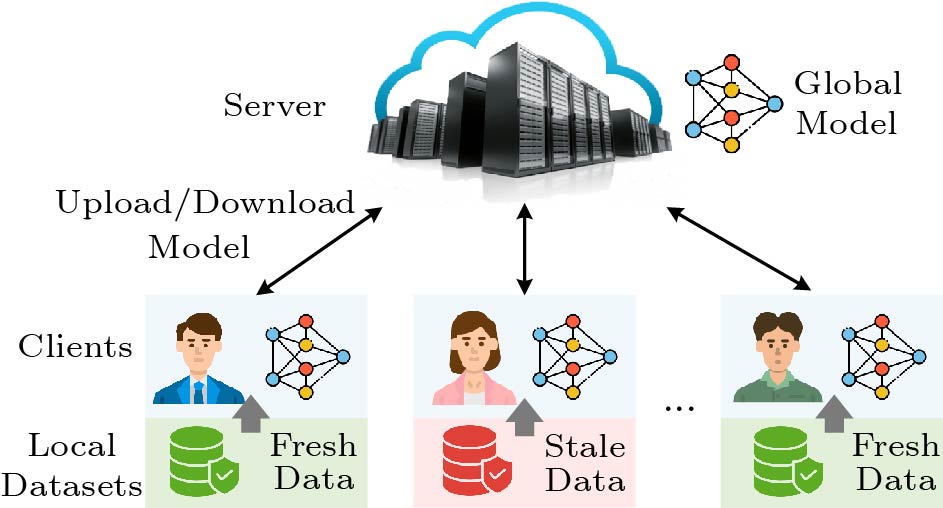
We consider an AoI-aware FL system[19], as depicted in Fig.1, which consists of a central server and a set of clients represented by N={1,2,...,N}. In traditional FL systems, the local dataset of each client is generally given in advance and will remain unchanged during the FL process. In contrast, our system allows clients to update their local datasets by spending some costs, enabling them to employ up-to-date data for local model training. The fresher the local datasets provided by clients, the more accurate the global model obtained by the FL system will be. Besides, the time is divided into T equivalent-length time slots, in each of which the server will conduct a round of federated learning under a predefined budget. For simplicity, we assume that the server has the same budget in each round, denoted by B, which can be easily extended to the case of heterogeneous budgets. More specifically, the joint training process in the AoI-aware FL system can be roughly described as the following steps. For ease of reference and understanding, we list major notations in Table 1.
1) Client Selection for Updating Data. The server selects a subset of clients Nt(⊆N) to update their local datasets at the beginning of each time slot t∈T={1,2,...,T}. For each client i∈Nt, we denote its local dataset as Dit, which can be regarded as the data collected from some fixed point of interests or purchased from some preferred data owners by client i. The dataset might be updated on-demand by the client, so it might vary over different time slots. For simplicity, we assume that the dataset of client i across different time slots remains the same size (denoted by ni). This assumption is rational since we can randomly sample the same number of data items from different sizes of datasets. Moreover, each client might spend some costs in obtaining its local dataset, so the server will pay a reward, denoted by pi, to client i as the compensation. Meanwhile, the server publicizes global model parameters, denoted by \boldsymbol\omega_{t-1} , to all clients for their local training. \boldsymbol\omega_{t-1} is the result of the (t-1) -th round of federated learning, and we use \boldsymbol\omega_{0} to represent the initial global model parameter.
2) Local Training. Each client i \in \mathcal{N} performs local training after receiving the global model parameter \boldsymbol\omega_{t-1} from the server. The loss function of local training for client i can be described as
\begin{array}{*{20}{l}} F_{t,\ i}(\boldsymbol\omega;\mathcal{D}_t^i) = \dfrac{1}{n_i} \displaystyle\sum\limits_{x \in \mathcal{D}_t^i}f(\boldsymbol\omega;x), \end{array} where \boldsymbol\omega is the model parameter, \mathcal{D}_t^i is the local training dataset, n_i is the data size of \mathcal{D}_t^i , and f(\cdot) is a server-specified loss function, e.g., mean absolute loss, mean squared loss, or cross entropy loss. Then, based on the received global model parameter \boldsymbol\omega_{t-1} , client i performs \tau steps of mini-batch stochastic gradient descent to compute its local model parameter \boldsymbol\omega_{t}^{i} as:
\begin{array}{*{20}{l}} \boldsymbol\omega_{t}^{i,\ k+1} = \boldsymbol\omega_{t}^{i,\ k} - \eta_{t} \nabla F_{t,\ i}(\boldsymbol\omega_{t}^{i,\ k};\xi_{t}^{i,\ k}), \end{array} (1) where k = \{0,..., \tau - 1\} , \xi_{t}^{i,\ k} is the k -th mini-batch sampled from \mathcal{D}_{t}^{i} , and \eta_{t} is the learning rate in the t -th round. In (1), there is \boldsymbol\omega_{t}^{i,\ \tau} = \boldsymbol\omega_{t}^{i} and \boldsymbol\omega_{t}^{i,\ 0} = \boldsymbol\omega_{t-1} . Finally, client i uploads \boldsymbol\omega_{t}^{i} to the server.
3) Model Aggregation. As shown in (2), the server aggregates the received local model parameters to obtain the global model parameter \boldsymbol\omega_{t} , i.e.,
\begin{array}{*{20}{l}} \boldsymbol\omega_{t} = \displaystyle\sum\limits_{i=1}^{N}\frac{n_i}{n} \boldsymbol\omega_{t}^{i}, \end{array} (2) where n=\sum_{i=1}^{N} n_i is the total quantity of training data in each time slot. Then, the server sends the updated global model \boldsymbol\omega_{t} back to each client for the next round of local training. The above steps of FL will be repeated until the total time is exhausted.
Overall, the global loss function is defined as:
\begin{array}{*{20}{l}} F(\boldsymbol\omega) \triangleq \dfrac{1}{T} \displaystyle\sum_{t=1}^{T}\displaystyle\sum\limits_{i=1}^{N}\dfrac{n_i}{n} F_{t,\ i}(\boldsymbol\omega;\mathcal{D}_{t}^i). \end{array} The goal of the whole FL system is to obtain the optimal model parameter vector \boldsymbol\omega^* so as to minimize the global loss function, i.e., \boldsymbol\omega^* = \mathop{\arg\min}\nolimits_{\boldsymbol\omega}F(\boldsymbol\omega).
2.2 Problem Formulation
In this paper, we focus on the data freshness in FL systems. Drawing inspiration from sensing systems, we employ the concept of AoI to quantify the freshness of clients' local datasets. In this context, AoI is defined as the elapsed time since the local data was generated. To be specific, let the current round of FL be in the t -th time slot and u_i(t) be the latest update time slot of client i 's local dataset \mathcal{D}_{t}^{i} . Then, we use (3) to express the AoI value of the dataset \mathcal{D}_{t}^{i} (referred to as client i 's AoI for simplicity), i.e.,
\begin{array}{*{20}{l}} \Delta_{i}(t)= t - u_{i}(t). \end{array} (3) Especially, \Delta_{i}(0) = 0 for all clients. Furthermore, the dynamics of client i 's AoI can be described as follows:
\begin{array}{*{20}{l}} \Delta_i(t)=\left\{ \begin{split} & \Delta_i(t-1) + 1 \ , \quad i \notin \mathcal{N}_t, \\& 0 \ ,\qquad\qquad\qquad\quad \text{otherwise}. \end{split} \right. \end{array} (4) It is important to highlight that different client selection strategies can result in various local data freshness even for the same client. Moreover, these client selection strategies can significantly influence the loss of the global model, as the freshness of local data directly impacts the quality of local training. Our objective is to minimize the loss of the global model after the whole FL process by carefully selecting the optimal client set \mathcal{N}_t in each time slot t \in \mathcal{T} while adhering to the constraint of the limited budget B . Notably, the client selection strategies considered in this paper are non-anticipative, i.e., these are strategies that do not use future knowledge in selecting clients. To formally represent these strategies, we define A^{\pi}(t) =\{a_1^{\pi}(t),..., a_N^{\pi}(t)\} ( t \in \mathcal{T} ) to indicate the selection status of each client in the t -th time slot. Specifically, if a_i(t) = 1 , it implies that client i is selected in the time slot (i.e., i \in \mathcal{N}_t ); conversely, if a_i(t) = 0 , it signifies that client i falls outside \mathcal{N}_t (i.e., i \notin \mathcal{N}_t ). Then, we can formulate the problem as:
\begin{array}{*{20}{l}} &{\text{P1}} :\ \ \ \ \ \ \ \ \min\limits_{\pi \in \Pi}\ \mathbb{E}(F(\boldsymbol\omega_T))-F^* , \end{array} (5) \begin{array}{*{20}{l}} &\rm{s.t.}\ \ \ \ \ \ a_i^{\pi}(t) \in \{0,1\}, \forall i \in \mathcal{N}, \forall t \in \mathcal{T}, \end{array} (6) \begin{array}{*{20}{l}} &\quad \quad \ \Delta_{i}(t)= \mathbb{1}_{\{a_i^{\pi}(t)=0\}} \left(\Delta_{i}(t-1)+1\right), \end{array} (7) \begin{array}{*{20}{l}} &\ \ \ \ \ \ \ \ \ \ \displaystyle\sum\limits_{i=1}^{N} a_i^{\pi}(t)p_i \leqslant B,\ \forall t \in \mathcal{T}. \end{array} (8) Here, \boldsymbol\omega_T in (5) is the aggregated global model after T rounds, F^*=F(\boldsymbol\omega^*) is the optimal global loss, and \mathbb{E}[F(\boldsymbol\omega_T)]-F^* is the gap between the expected global loss after T rounds and F^* . Naturally, the closer \mathbb{E}[F(\boldsymbol\omega_T)]-F^* is to zero, the better is the performance of \boldsymbol\omega_T . The constraint in (6) indicates that each client can only be selected at most once by the server for updating its local dataset in each time slot. (7) is the reformulation of (4), i.e., the dynamics of each client's AoI, where \mathbb{1}_{\{\cdot\}} is an indicator function. (8) restricts the cost of the server, i.e., the total payment cannot exceed the budget in each round.
Table 1. Description of Major NotationsVariable Description i,t Index of client and time slot, respectively \mathcal{N},\mathcal{T} Set of clients and time slots, respectively \mathcal{N}_t Set of selected clients in time slot t \mathcal{D}_t^i Local dataset of client i in time slot t F(\boldsymbol\omega) Global loss function with parameter vector \boldsymbol\omega F_{t,\ i}(\boldsymbol\omega) Loss function of client i in time slot t \boldsymbol\omega_0,\boldsymbol\omega^* Initial and optimal model parameter vector \boldsymbol\omega_t,\boldsymbol\omega_t^i Global model parameter vector and local model parameter vector of client i in time slot t, respectively n_i,n Size of client i's local dataset and total size of all clients' local datasets, respectively k,\tau Index and total number of local iterations, respectively \xi_{t}^{i,k} The k-th mini-batch sampled from \mathcal{D}_{t}^{i} \eta_t Learning rate in time slot t \bar{\eta},\widetilde{\eta} Minimum and maximum of the learning rate, respectively p_i Payment of client i for obtaining fresh data B Budget of the server per time slot u_i(t) Latest update time slot of the dataset \mathcal{D}_{t}^{i} \Delta_{i}(t) AoI value of client i in time slot t Solving Problem P1, however, is quite challenging due to the following two aspects. On the one hand, we do not know how the clients' AoI values will affect the final model parameter \boldsymbol\omega_{T} and the corresponding loss function \mathbb{E}[F(\boldsymbol\omega_{T})] before we actually conduct the FL process. Hence, we need to analyze the internal connection between them as we will show later. On the other hand, the client selections across different rounds of FL are not independent, i.e., each client selection operation will be affected by those in previous rounds due to the dynamics of AoI, which makes the design of the client selection strategy much more intractable.
3. Convergence Analysis
To identify the impact of each client's AoI on the global model, we perform a rigorous convergence analysis of our AoI-aware FL system. We start with several important assumptions on the local loss function.
Assumption 1. For all t\in \{1,2,...,T\} , i\in \{1,2,..., N\} , F_{t,\ i} is \beta -smooth, that is, for \forall \;\; \boldsymbol\omega_{1} , \boldsymbol\omega_{2} , F_{t,\ i}(\boldsymbol\omega_{2})-F_{t,\ i}(\boldsymbol\omega_{1}) \,\leqslant \,\left\lt\nabla F_{t,\ i}(\boldsymbol\omega_{1}), \ \boldsymbol\omega_{2}\,-\,\boldsymbol\omega_{1} \right \gt\;+\;({\beta }/2)\Vert \boldsymbol\omega_{2}-\boldsymbol\omega_{1} \Vert^{2} .
Assumption 2. For all t \in \{1,2,...,T\} , i \in \{1,2,..., N\} , F_{t,\ i} is \mu -strongly convex, i.e., for \forall \;\; \boldsymbol\omega_{1} , \boldsymbol\omega_{2} , F_{t,\ i}(\boldsymbol\omega_{2})\;-\;F_{t,\ i}(\boldsymbol\omega_{1})\geqslant\left\lt\nabla F_{t,\ i}(\boldsymbol\omega_{1}), \ \boldsymbol\omega_{2}-\boldsymbol\omega_{1} \right\gt + ({\mu}/2)\;\Vert \boldsymbol\omega_{2} - \boldsymbol\omega_{1} \Vert^{2} .
Assumption 3. For all t\in \{1,2,...,T\} , i\in \{1,2,..., N\} , the stochastic gradients of the loss function is unbiased, i.e., \mathbb{E}_{\xi}(\nabla F_{t,\ i}(\boldsymbol\omega;\xi)) = \nabla F_{t,\ i}(\boldsymbol\omega) .
Assumption 4. For all t \in \{1,2,...,T\} , i \in \{1,2, ..., N\} , the expected squared norm of stochastic gradients is bounded, i.e., \mathbb{E}_{\xi}\Vert \nabla F_{t,\ i}(\boldsymbol\omega;\xi) \Vert^2 \leqslant G_i^2 + \Delta_{i}(t)\sigma_i^2 .
Assumptions 1–3 are commonly adopted in various existing convex federated learning studies[20, 21]. These assumptions ensure that the gradient of F_{t,\ i}(\boldsymbol\omega) does not change too rapidly or slowly with respect to \boldsymbol\omega , and that the stochastic gradients sampled from local datasets are unbiased. It is worth noting that models with convex loss functions like logistic regression (LR)[22] and support vector machines (SVM)[23] adhere to Assumption 2. The evaluation results in Section 5 demonstrate that our algorithm also performs well with non-convex loss functions, e.g., convolutional neural network (CNN)[24].
Assumption 4, however, is a novel assumption we made for our AoI-aware FL system. Unlike the general assumptions made in other FL systems, which assume that \mathbb{E}_{\xi}\Vert \nabla F_{t,\ i}(\boldsymbol\omega;\xi) \Vert^2 is bounded by an inherent bound G_i^2 of client i , we take the impact of the client's AoI on model training into consideration. More, specifically, we assume that the upper bound of \mathbb{E}_{\xi}\Vert \nabla F_{t,\ i}(\boldsymbol\omega;\xi) \Vert^2 is positively correlated with \Delta_{i}(t) , and the coefficient \sigma_i^2 reflects the sensitivity of client i 's local dataset to freshness. The potential insight is that a smaller AoI value means a fresher local dataset and that better models can be trained, which is consistent with a smaller gradient norm indicating a better model performance when the loss function is convex[19]. Particularly, if the server selects client i to update its local dataset in round t , meaning \Delta_{i}(t)=0 , Assumption 4 will degrade to \mathbb{E}_{\xi}\Vert \nabla F_{t,\ i}(\boldsymbol\omega;\xi) \Vert^2 \leqslant G_i^2 , which is consistent with assumptions in prior work[20, 21]. It is noteworthy that all three loss functions (mean absolute loss, mean squared loss, or cross-entropy loss) satisfy Assumptions 1–4.
Theorem 1 (Convergence Upper Bound[19]). For the sake of clarity, we define \bar{\eta}= \mathop{\min}_{t}\{\eta_t\} and \widetilde{\eta}= \mathop{\max}_{t}\{\eta_t\} . Meanwhile, we suppose that Assumptions 1–4 hold and the step size meets \bar{\eta} < {2}/{\mu} . Then, the FL training loss after the initial global model \boldsymbol\omega_{0} is updated using (2) for T rounds, which satisfies:
\begin{split} &\mathbb{E}(F(\boldsymbol\omega_T)) - F^* \leqslant \dfrac{\beta}{2}(1-\dfrac{\mu \bar{\eta}}{2})^{T}\Vert \boldsymbol\omega_{0} - \boldsymbol\omega^*\Vert^2 +\\ & \ \ \ \ \ \ \ \ \ \ \dfrac{ \beta}{2} \sum_{t=1}^{T}\sum_{i=1}^{N}\alpha_i\left(G_i^2+\Delta_{i}(t)\sigma_i^2\right), \end{split} (9) where
\alpha_i = \frac{\widetilde{\eta} n_i}{\mu n}+N\widetilde{\eta}\left(\tau^2\widetilde{\eta}+\frac{2(\tau -1)^2}{\mu}\frac{n_i^2}{n^2} \right). Theorem 1 explicitly outlines the relationship between various factors and the global loss in our AoI-aware FL system[19]. The first term of the upper bound geometrically decreases with the total number of rounds T , implying that the stochastic gradient descent makes progress towards the optimal solution. The second term of (9) is determined by the AoI value of each client's local dataset in each round. The fresher the local dataset is, the smaller the value of \Delta_{i}(t) and the second term will be. Moreover, as the coefficients in the second term depend on the aggregation weight {n_i}/{n} , a client with more local data has a larger impact on the training loss than those with less local data.
4. Problem Deduction and Algorithm Design
In this section, we propose the client selection algorithm, named WICS. First, we utilize the convergence upper bound to transform the optimization objective of Problem P1. To minimize the average AoI value, we then formulate the AoI minimization problem as a restless multi-armed bandit (RMAB) problem[25]. Subsequently, we relax the RMAB problem and employ the Lagrangian Dual approach to decouple it down into subproblems. Next, we determine the optimal strategy for each of these decoupled problems. Finally, we derive a closed-form expression for the Whittle's index and present a detailed algorithm.
4.1 Problem Transformation
According to Theorem 1, we obtain the convergence bound of the global model after T rounds. It is not difficult to observe that we can regulate the convergence of the FL process by controlling the right side of (9). Therefore, we can convert Problem P1 by minimizing the second term of the convergence upper bound. After neglecting the constant term, the objective of Problem P1 can be converted as follows:
\begin{array}{*{20}{l}} &\min\limits_{\pi \in \Pi} \dfrac{1}{TN} \displaystyle\sum\limits_{t=1}^{T}\displaystyle\sum\limits_{i=1}^{N} \phi_i\Delta_{i}(t),\ \phi_i = \dfrac{\alpha_i \sigma_i^2 \beta TN}{2}. \end{array} (10) It is important to note that the weight \phi_i in (10) is dependent on \alpha_i and \sigma_i^2 , and \alpha_i is closely associated with n_i . This signifies that the size of the local dataset and its sensitivity to data freshness will significantly affect the client selection results during the FL process.
Based on the above analysis, we can convert Problem P1 into Problem P2, which is shown as follows:
\begin{array}{*{20}{l}} & {\text{P2}} :\ \ \ \min\limits_{\pi \in \Pi}\ \dfrac{1}{TN} \displaystyle\sum\limits_{t=1}^{T}\displaystyle\sum\limits_{i=1}^{N}\phi_i\Delta_{i}(t), \end{array} (11) \begin{array}{*{20}{l}} &\ \ \ \ \ \rm{s.t.}\ \ \ a_i^{\pi}(t) \in \{0,1\}, \forall i \in \mathcal{N}, \forall t \in \mathcal{T}, \end{array} (12) \begin{array}{*{20}{l}} &\quad \quad \quad\ \quad\quad \Delta_{i}(t)= \mathbb{1}_{\{a_i^{\pi}(t)=0\}} \left(\Delta_{i}(t-1)+1\right), \end{array} (13) \begin{array}{*{20}{l}} & \displaystyle\sum\limits_{i=1}^{N}a_i^{\pi}(t)p_i \leqslant B,\ \forall t \in \mathcal{T}. \end{array} (14) 4.2 RMAB Modeling and Solution
To address Problem P2 (i.e., (11), (12), (13), and (14)), we formulate it as an RMAB problem by utilizing the stochastic control theory. Unlike classic multi-armed bandit problems[26], where the unused arms neither yield rewards nor change states and the states of all arms are known at any time, the arms in RMAB might still change states according to various transition rules even when they are not being pulled. In this paper, each client is seen as a restless bandit, and the corresponding AoI value is regarded as the state[19]. Note that the AoI value evolves in every time slot, even if the client is not selected. Unfortunately, the RMAB problem is usually PSPACE-hard (Polynomial Space Hard)[25]. Thus, we employ Whittle's methodology to address this problem[27].
Firstly, we relax Problem P2 by replacing the budget constraint (i.e., (14)) with a relaxed version:
\frac{1}{TN} \sum_{t=1}^{T}\sum_{i=1}^{N}a_i^{\pi}(t)\frac{p_i}{B} \leqslant \frac{1}{N},\ \forall t \in \mathcal{T}. Then, we leverage the Lagrangian Dual approach to transform Problem P2 into a max-min problem, which can be represented by (15), (16), (17), and (18), i.e.,
\begin{array}{*{20}{l}} & {\text{P3}} : \ \ \ \max_{\lambda}\min_{\pi \in \Pi}\mathcal{L}(\pi,\lambda), \end{array} (15) \begin{array}{*{20}{l}} &\rm{s.t.} \ \ \ \ a_i^{\pi}(t) \in \{0,1\}, \forall i \in \mathcal{N}, \forall t \in \mathcal{T}, \end{array} (16) \begin{array}{*{20}{l}} &\quad \quad \quad\quad \ \Delta_{i}(t)= \mathbb{1}_{\{a_i^{\pi}(t)=0\}} \left(\Delta_{i}(t-1)+1\right), \end{array} (17) \begin{array}{*{20}{l}} & \lambda \geqslant 0. \end{array} (18) Here, the Lagrange dual function \mathcal{L}(\pi,\lambda) is given by
\begin{split} \mathcal{L}(\pi,\lambda)&= \dfrac{\sum\limits_{t=1}^{T}\sum\limits_{i=1}^{N}\phi_i\Delta_{i}(t)}{TN}+ \lambda\left(\dfrac{1}{TN} \sum\limits_{t=1}^{T}\sum\limits_{i=1}^{N}a_i^{\pi}(t)\dfrac{p_i}{B} - \dfrac{1}{N} \right) \\& =\dfrac{1}{TN} \sum\limits_{t=1}^{T}\sum\limits_{i=1}^{N}\left(\phi_i\Delta_{i}(t)+ \lambda a_i^{\pi}(t)\dfrac{p_i}{B} \right) -\dfrac{\lambda}{N}\\& = \dfrac{1}{N} \sum\limits_{i=1}^{N}\dfrac{1}{T}\left(\sum\limits_{t=1}^{T}\left(\phi_i\Delta_{i}(t) + \lambda a_i^{\pi}(t)\dfrac{p_i}{B} \right)\right)-\dfrac{\lambda}{N}, \end{split} where \lambda is the Lagrange multiplier.
In order to tackle Problem P3, we need to address the problem \min_{\pi \in \Pi}\mathcal{L}(\pi,\lambda) first. This involves finding the optimal client selection strategy \pi^* that minimizes \mathcal{L}(\pi,\lambda) for any given \lambda . Notably, we can ignore the constant term {\lambda}/{N} and focus on solving \mathcal{L}(\pi,\lambda) for each individual client separately. This problem associated with each client is actually a decoupled problem, in which the goal is to decide whether or not the client should be selected to update its local dataset in each time slot. Specifically, we formalize the decoupled problem over an infinite time-horizon as:
\begin{array}{*{20}{l}} & {\text{P4}} :\min\limits_{\pi \in \Pi}\left\{\lim\limits_{T \to +\infty} \dfrac{1}{T} \displaystyle\sum\limits_{t=1}^{T}\left(\dfrac{B \phi_i}{p_i}\Delta_{i}(t)+\lambda a_i^{\pi}(t) \right)\right\}, \end{array} (19) \begin{array}{*{20}{l}} & \rm{s.t.} \ \ \ a_i^{\pi}(t) \in \{0,1\}, \forall i \in \mathcal{N}, \forall t \in \mathcal{T}, \end{array} (20) \begin{array}{*{20}{l}} & \Delta_{i}(t)= {\mathbb{1}}_{\{a_i^{\pi}(t)=0\}} \left(\Delta_{i}(t-1)+1\right), \end{array} (21) \begin{array}{*{20}{l}} & \lambda \geqslant 0. \end{array} (22) Then, we begin to deal with the decoupled problem (i.e., (19), (20), (21), and (22)) by modeling it as a Markov decision process (MDP). This process consists of the AoI state \Delta_{i}(t) , the control variable a_i^{\pi}(t) , the state transition functions \mathbb{P}(\cdot) , and the cost function \mathbb{C}_i(\cdot) . Specifically, the state transition from time slot t to time slot t+1 in MDP is deterministic, which can be described by (23), i.e.,
\begin{array}{*{20}{l}} &\mathbb{P}(\Delta_{i}(t+1)=\Delta_{i}(t)+1|a_i^{\pi}(t)=0)=1, \\ &\mathbb{P}(\Delta_{i}(t+1)=0|a_i^{\pi}(t)=0)=0, \\ &\mathbb{P}(\Delta_{i}(t+1)=\Delta_{i}(t)+1|a_i^{\pi}(t)=1)=0, \\ &\mathbb{P}(\Delta_{i}(t+1)=0|a_i^{\pi}(t)=1)=1. \end{array} (23) In addition, we regard the objective of Problem P4 as the cost function of MDP. In other words, the cost function on the state transition from time slot t to time slot t+1 can be defined as:
\begin{array}{*{20}{l}} C_i(\Delta_{i}(t),a_i^{\pi}(t)) \triangleq ({B \phi_i}/{p_i})\Delta_{i}(t)+\lambda a_i^{\pi}(t), \end{array} (24) where the first term of (24) is related to the resulting AoI value in time slot t . To make the presentation clearer, we regard the Lagrange multiplier \lambda as a kind of service charge for client i under the MDP model, which is incurred only when a_i^{\pi}(t)=1 . Note that the cost function and the service charge are not the real charge and cost, which will only be mentioned in MDP.
Finally, we derive the optimal strategy of this MDP and prove that it is a special type of deterministic strategy, which is shown as follows.
Theorem 2 (Optimal Strategy for Problem P4[19]). Consider the decoupled model over an infinite time-horizon. The optimal strategy \pi^* for Problem P4 is selecting client i in each time slot t to update its local dataset only when \Delta_{i}(t)>H_i-1 , where
\begin{array}{*{20}{l}} H_i = \left \lfloor -\dfrac{1}{2}+\sqrt{\dfrac{1}{4}+\dfrac{2\lambda p_i}{B \phi_i}} \right \rfloor. \end{array} (25) It is worth noting that the threshold H_i in (25) is a function of the service charge \lambda . Intuitively, we expect that the server selects client i when \Delta_{i}(t) is high to reduce the AoI value and does not select client i when \Delta_{i}(t) is low so as to avoid the service charge \lambda [19].
4.3 The WICS Algorithm
Our ultimate objective is to solve the Lagrange dual function for Problem P3, i.e., \max_{\lambda}\min_{\pi \in \Pi}\mathcal{L}(\pi,\lambda) . Now, according to Theorem 2, we can obtain the optimal strategy \pi^* as the solution of \min_{\pi \in \Pi}\mathcal{L}(\pi,\lambda) for any given \lambda . Then, we need only to concentrate on the problem of \max_{\lambda}\mathcal{L}(\pi^*,\lambda) , i.e., finding an optimal \lambda to maximize \mathcal{L}(\pi^*,\lambda) . Nevertheless, solving this problem optimally is a complex task, and we can only approximately address it by employing the Whittle's index methodology[27]. More specifically, we still decouple the problem \max_{\lambda}\mathcal{L}(\pi^*,\lambda) to find an individual \lambda parameter for each client i separately, denoted by \lambda_i .
After decoupling Problem P3, we turn to maximize
\frac{1}{T} \sum_{t=1}^{T}\left(\frac{B \phi_i}{p_i}\Delta_{i}(t)+\lambda_i a_i^{\pi^*}(t)-\frac{B \lambda_i}{Np_i} \right), for each client i separately, where \lambda_i might differ among clients. Actually, it is a monotonic increasing function of \lambda_i when given an initial state \Delta_{i}(0)=0 . Furthermore, \lambda_i needs to satisfy the condition of Theorem 2, i.e., \Delta_{i}(t) > H_i-1 , which indicates that \lambda_i is bounded in each time slot. Therefore, \lambda_i will maximize the average value of
\frac{1}{T}\sum_{t=1}^T\left(\frac{B\phi_i}{p_i}\Delta_i(t)+\lambda_ia_i^{\pi^*}(t)-\frac{B\lambda_i}{Np_i}\right), when \Delta_{i}(t)=H_i-1 . We use the notation WI_{i,\ t} [19] to express this critical value, and the closed-form expression of WI_{i,\ t} can be derived as follows:
\begin{array}{*{20}{l}} {WI_{i,\ t}\triangleq} \ \lambda_i(\Delta_{i}(t)) = \dfrac{(\Delta_{i}(t)+1)(\Delta_{i}(t)+2)B \phi_i}{2p_i}, \end{array} (26) where WI_{i,\ t} stands for client i 's Whittle's index (WI) in time slot t . Note that \sigma_i^2 and n_i are included in \phi_i , so that the index WI_{i,\ t} is dependent on \sigma_i^2, \ n_i , B , and \Delta_{i}(t) . Since \sigma_i^2,\ n_i , and B are constants, WI_{i,\ t} is essentially a function of \Delta_{i}(t) . This indicates that \lambda_i can also be seen as a function of \Delta_{i}(t) . In general, the Whittle's index is not the same for different clients, which means that the values of \lambda_i that optimize different decoupled problems will be heterogeneous.
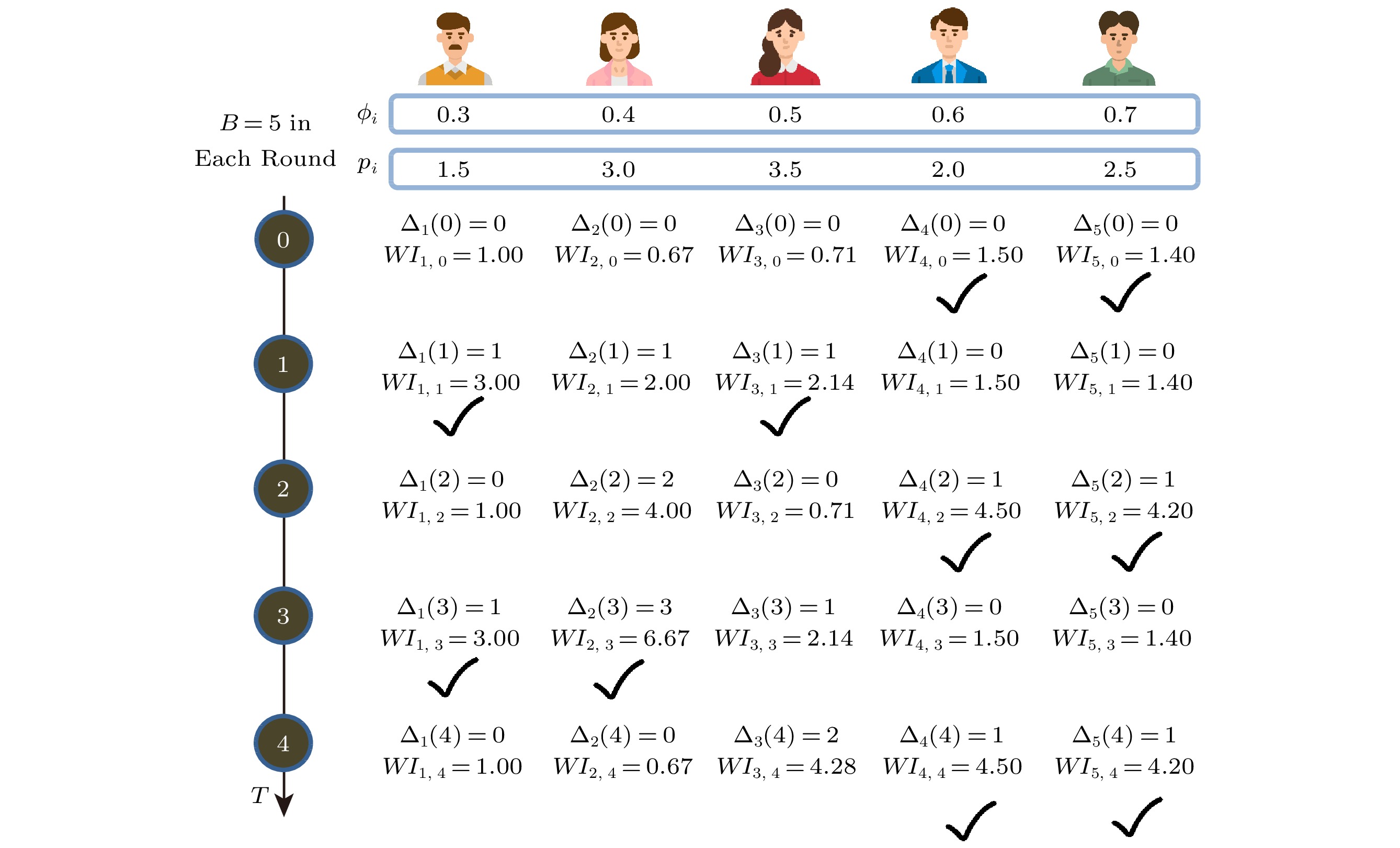
According to the Whittle's index, we can now design the WICS algorithm to address Problem P3 (and also Problem P2 based on the Lagrange duality). The fundamental idea is to select clients with higher WI values in each time slot while ensuring that the budget is not exceeded. As outlined in Algorithm 1, we first compute the WI value for each client using (26) and then sort all clients in \mathcal{N} into the set (i_1, i_2,..., i_N) such that WI_{i_1,\ t} \geqslant WI_{i_2,\ t} \geqslant... \geqslant WI_{i_N,\ t} (steps 1–3). Subsequently, we greedily select clients into a winning set \mathcal{N}_t and allocate corresponding payments to the winning clients until the remaining budget cannot afford the next client (steps 4–10). For a better understanding, we provide a straightforward example to clearly present the key process of Algorithm 1, as depicted in Fig.2. In each round, we calculate the values of each client's AoI and WI. When setting the budget of the server as B=5 , we can effectively pick out suitable clients according to the sorted results of Whittle's indexes. In Fig.2, the check mark indicates that the client is selected in this round.
Algorithm 1. Whittle's Index Based Client Selection (WICS) Input: the set of clients' AoI values \{\Delta_{1}(t),...,\Delta_{N}(t)\}, the set of clients' weights \{\phi_1,...,\phi_N\}, the set of clients' payments \{p_1,...,p_N\}, the budget of the server B; Output: the index set of selected clients \mathcal{N}_{t+1}; 1: for each client i in \mathcal{N} do 2: Calculate its WI value WI_{i,\ t} according to (26) and send WI_{i,\ t} to the server; 3: end for 4: The server sorts the clients into (i_1,i_2,...,i_N) such that WI_{i_1,\ t}\geqslant WI_{i_2,\ t}\geqslant ... \geqslant WI_{i_N,\ t}, and initializes an empty set \mathcal{N}_{t+1} as well as k=1; 5: while k\leqslant N do 6: if \sum_{i \in \mathcal{N}_{t+1}}(p_i+ p_{i_k}) <B then 7: \mathcal{N}_{t+1} \gets \mathcal{N}_{t+1}\cup \{i_k\}; 8: end if 9: k=k+1; 10: end while Finally, we analyze the performance of the WICS algorithm. Obviously, the computational overhead of Algorithm 1 is dominated by the sorting operation on clients' WI values, so the complexity of WICS is O(N\log N) . Additionally, we define the ratio \rho^{\pi}\triangleq {U_B^{\pi}}/{L_B} to measure the performance of strategy \pi , where L_B is a lower bound to the optimal performance of Problem P2, and U_B^{\pi} is an upper bound to the performance of Problem P2 under the strategy \pi , and we say that the strategy \pi is \rho^{\pi} -optimal. Through theoretical analysis, the WICS algorithm satisfies the following theorem.
Theorem 3 (Approximate Optimality). The solution produced by the WICS algorithm to Problem P2 over an infinite time-horizon is \rho^{WI} -optimal, where
\begin{array}{*{20}{l}} \rho^{WI}<\dfrac{2M(9N-1)\displaystyle\sum\limits_{i=1}^{N}\phi_i}{N^2\phi_{\min}-M\displaystyle\sum\limits_{i=1}^{N}\phi_i}. \end{array} Here, M=\left \lfloor {B}/{p_{\max}} \right \rfloor , p_{\max}=\max\{p_i|i\in\mathcal{N}\} , and \phi_{\min}=\min\{\phi_i|i\in\mathcal{N}\} .
Recall that the objective of Problem P2 (i.e., (11)) is derived from the objective of Problem P1 (i.e., (5)) according to the convergence bound analysis of Theorem 1. Therefore, the WICS algorithm is at least \rho^{WI} -optimal for Problem P1.
5. Performance Evaluation
In this section, we evaluate the performance of the proposed WICS algorithm with extensive simulations on two real-world datasets.
5.1 Evaluation Methodology
1) Simulation Setup. We conduct extensive simulations using two widely used real datasets: MNIST[28] and Fashion-MNIST (FMNIST)[29]. The MNIST dataset comprises 60000 handwritten digits for training and 10000 for testing, while the FMNIST dataset contains 60000 images of fashion items for training and 10000 for testing. We consider both convex (e.g., LR and SVM) and non-convex (e.g., CNN) models. The CNN architecture consists of two convolution layers (32 and 64 channels) of size 5 \times 5 , each of which is followed by 2 \times 2 max pooling, two fully-connected layers with 3136 and 512 units, and a ReLU layer with 10 units. In our experiments, we vary the number of clients N from 10 to 40 and set N=10 by default. Meanwhile, the number of time slots is set as T = 200 . Then, we generate a simplified budget B for each time slot from the set \{25, 40, 55, 70\} , and we assume that the cost parameter p_i is proportional to the amount of local data while ensuring that the cost for each client does not exceed [5, 15] . Next, we initialize our model with \boldsymbol\omega_{0}={\bf0} and set the batch size as b=16 . Without loss of generality, we set the learning rate of LR and SVM to be \eta_t=0.005 and the learning rate of CNN to be \eta_t=0.01 for all time slots. Each client performs \tau = 10 local iterations. Afterward, we randomly select the weight \phi_i from the range of (0,1) according to (10), which is similar to the method adopted in [30]. To illustrate the impact of AoI on local data, we intentionally mislabel some local data for each client in each time slot. In other words, we mislabel more data if the client has a larger AoI value.
2) Algorithms for Comparison. Our WICS algorithm accounts for the freshness of local datasets in FL, making it distinct from existing algorithms that cannot be directly applied to our problem. To the best of our knowledge, the closest algorithm that can be adapted to our setting is the ABS algorithm proposed by [31]. The ABS algorithm is also an index-based strategy, but it considers the age-of-update instead of AoI. We need to modify the ABS algorithm to accommodate the concept of AoI in our model. More specifically, the modified ABS index of client i in time slot t is given by {\Delta_i(t)\phi_i}/{p_i} . Similar to our WICS strategy, the ABS algorithm selects clients with higher modified ABS index values in a greedy manner, meanwhile ensuring that the budget is not exceeded in each time slot. It is important to note that only the selected clients can participate in the current round of FL training. For the purpose of comparison, we also implement the MaxPack algorithm[32] and a random algorithm. The MaxPack algorithm directly selects clients with higher AoI values while guaranteeing the budget constraint in each time slot. The random algorithm means that the server will pick out clients randomly.
5.2 Evaluation Results
In this subsection, we train three models (i.e., LR, SVM, and CNN) on both MNIST and FMNIST to compare the performance of different algorithms. Notably, we conduct experiments with variant budget B , which shows a similar performance. Thus, we only illustrate the result of B=40 due to the limited space. Furthermore, unless otherwise stated, the number of clients is set as 10 in the following simulations.
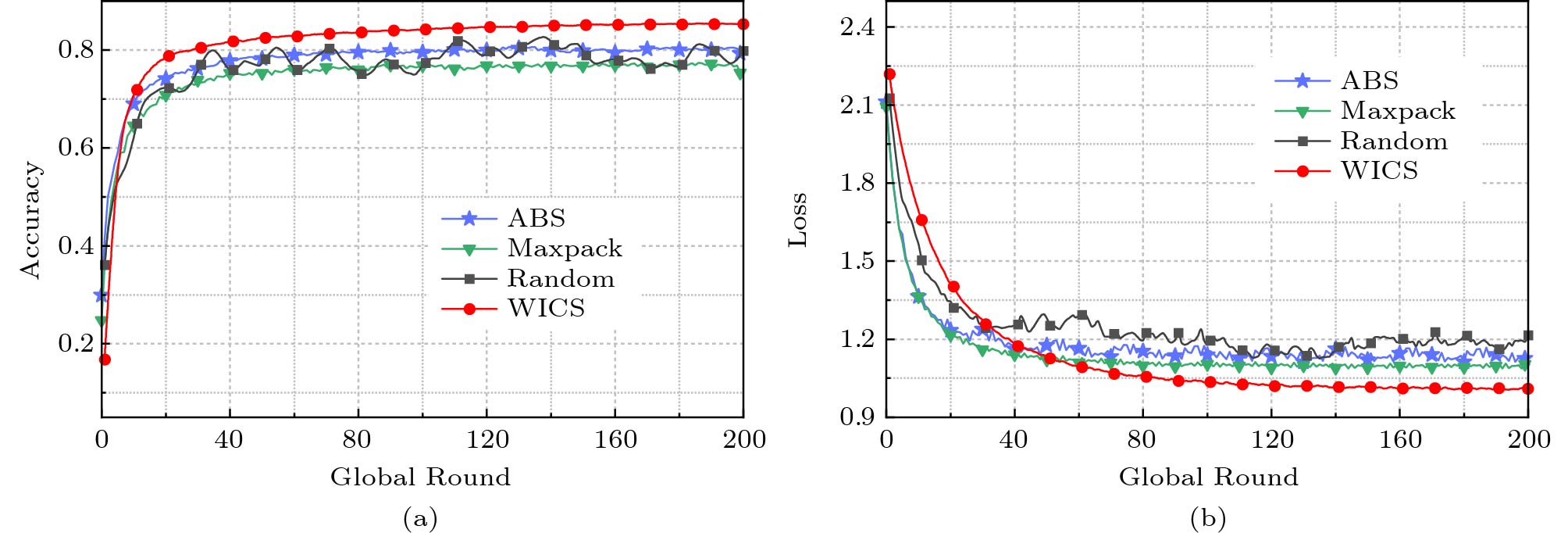
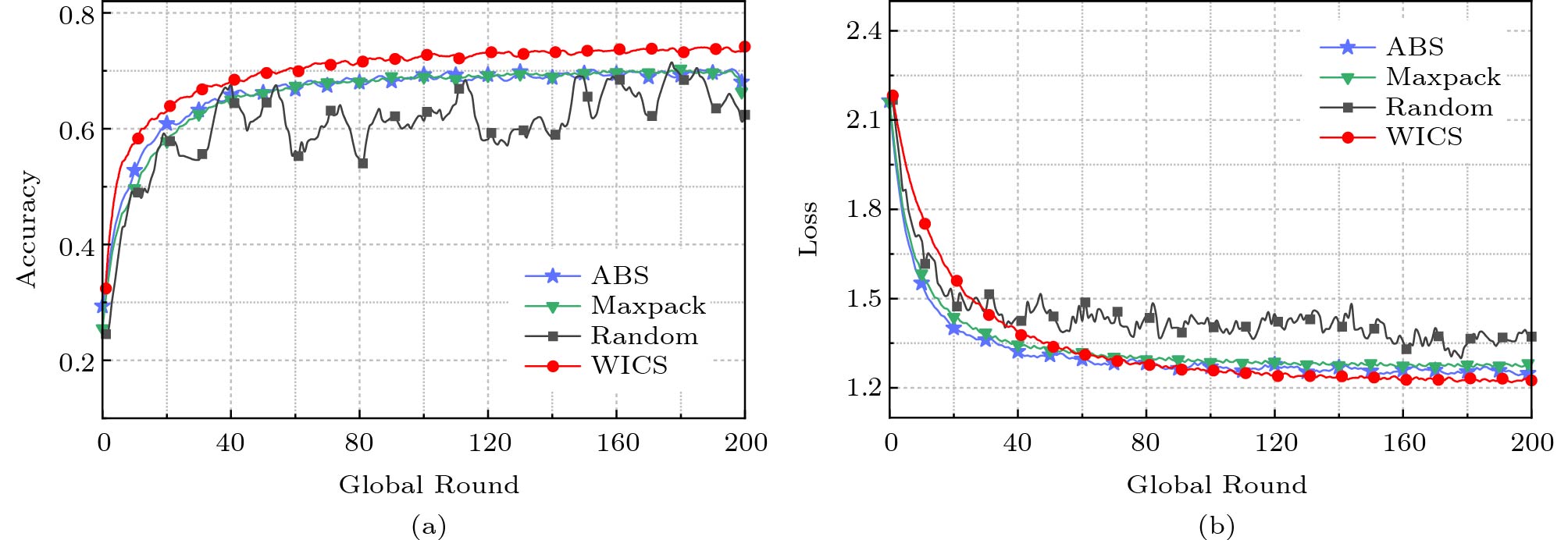
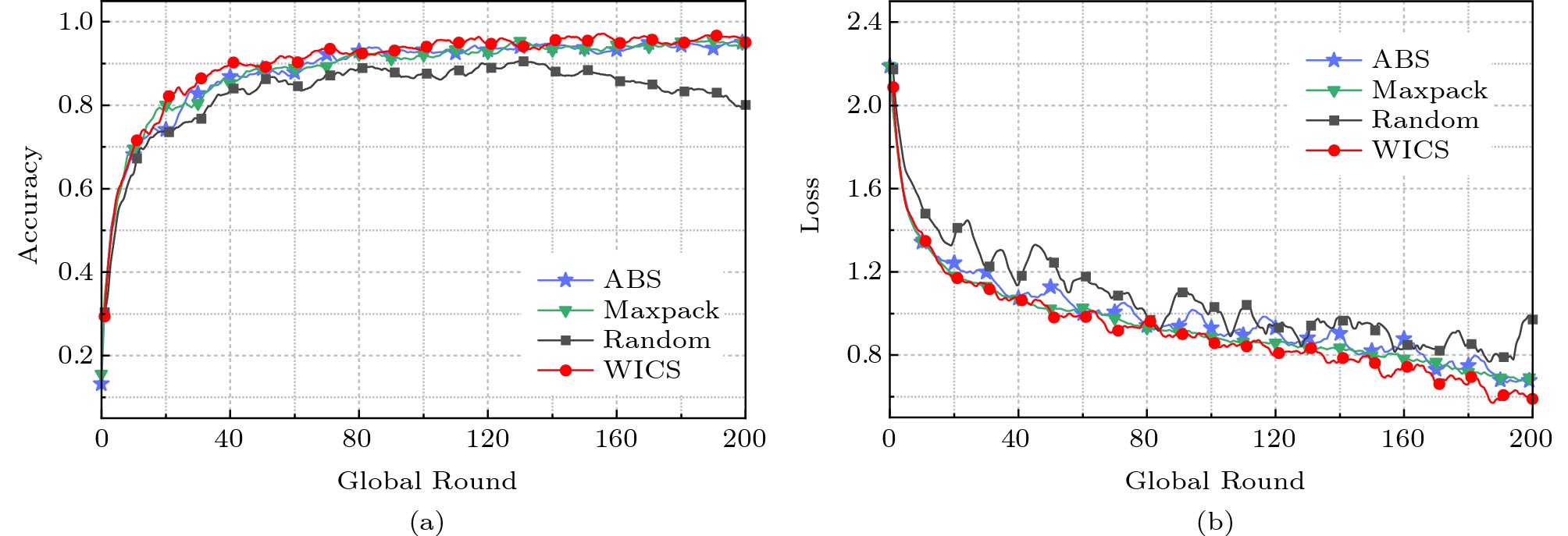
First, we evaluate the performance of various algorithms for LR on MNIST and FMNIST in terms of both accuracy and loss, as illustrated in Fig.3 and Fig.4, respectively. Accuracy measures the number of correct predictions, and loss quantifies the difference between the prediction and actual output. In Fig.3, we can observe that the achieved accuracy of all four algorithms gradually rises along with the increase of rounds, while the achieved loss of all four algorithms gradually decreases with the increase of rounds. It is noteworthy that the performance of WICS in terms of both accuracy and loss is better than those of the three compared algorithms. Similarly, we conduct a series of experiments to evaluate the performance of four algorithms under FMNIST. We also find that the results in Fig.4 are consistent with those in Fig.3.
![]() Figure 3. Performance of LR on MNIST[19]. (a) Accuracy. (b) Loss.
Figure 3. Performance of LR on MNIST[19]. (a) Accuracy. (b) Loss.![]() Figure 4. Performance of LR on FMNIST[19]. (a) Accuracy. (b) Loss.
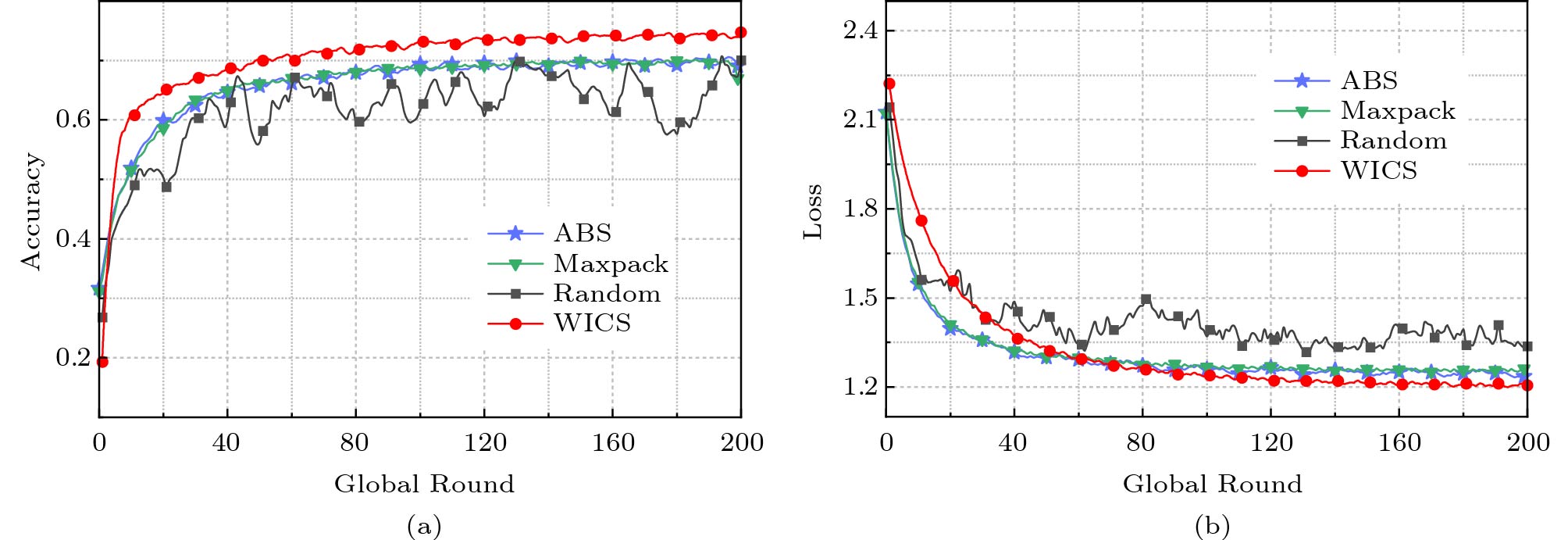
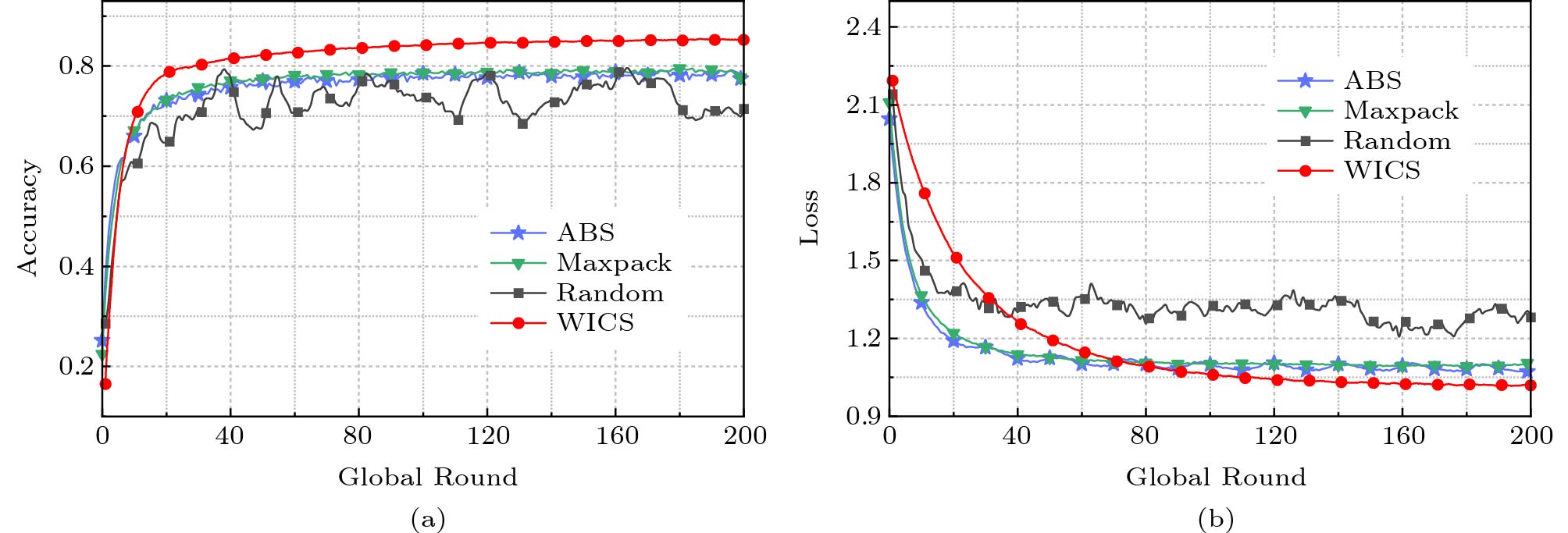
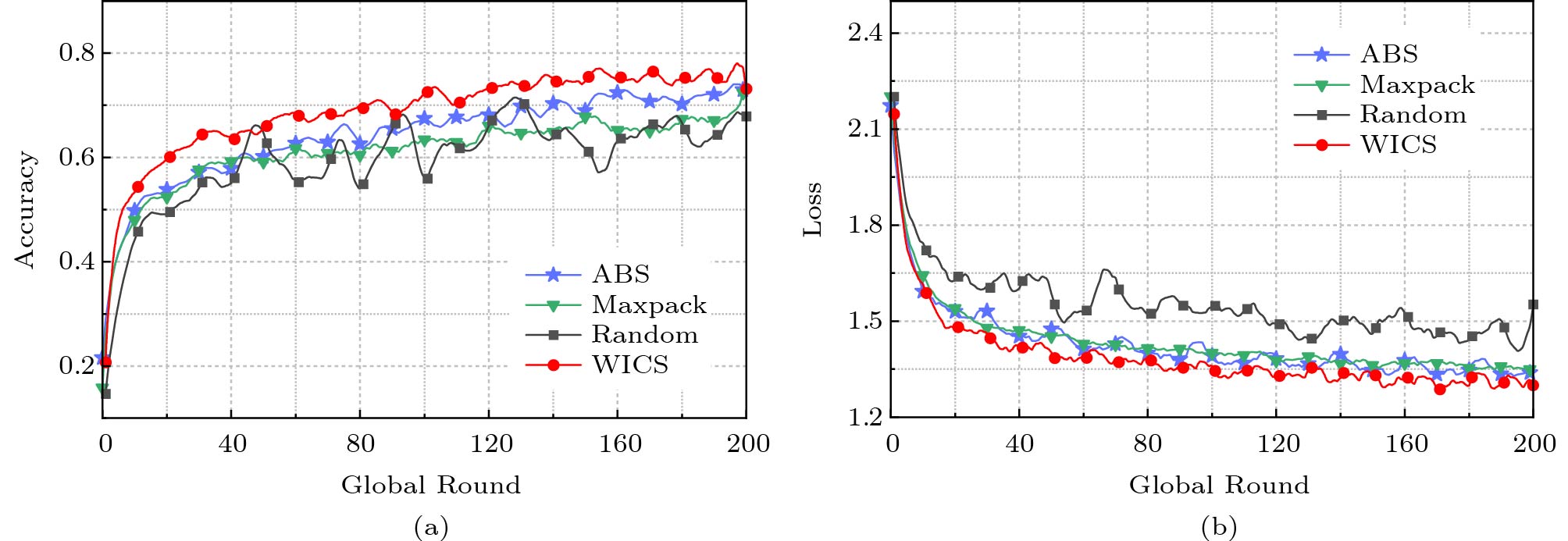
Figure 4. Performance of LR on FMNIST[19]. (a) Accuracy. (b) Loss.Next, we evaluate the performances of all four algorithms for SVM on MNIST and FMNIST in terms of both accuracy and loss, as depicted in Figs.5 and 6. We see that WICS can also achieve the best results in all algorithms. This indicates that WICS is effective for the models with a convex loss function, aligning with the theoretical convergence bound. To verify the effectiveness of WICS when the loss function is non-convex, we further conduct a series of simulations with CNN on MNIST and FMNIST. Figs.7 and 8 illustrate that WICS can still outperform other algorithms when the loss function does not satisfy the convex assumption.
![]() Figure 7. Performance of CNN on MNIST[19]. (a) Accuracy. (b) Loss.
Figure 7. Performance of CNN on MNIST[19]. (a) Accuracy. (b) Loss.![]() Figure 8. Performance of CNN on FMNIST[19]. (a) Accuracy. (b) Loss.
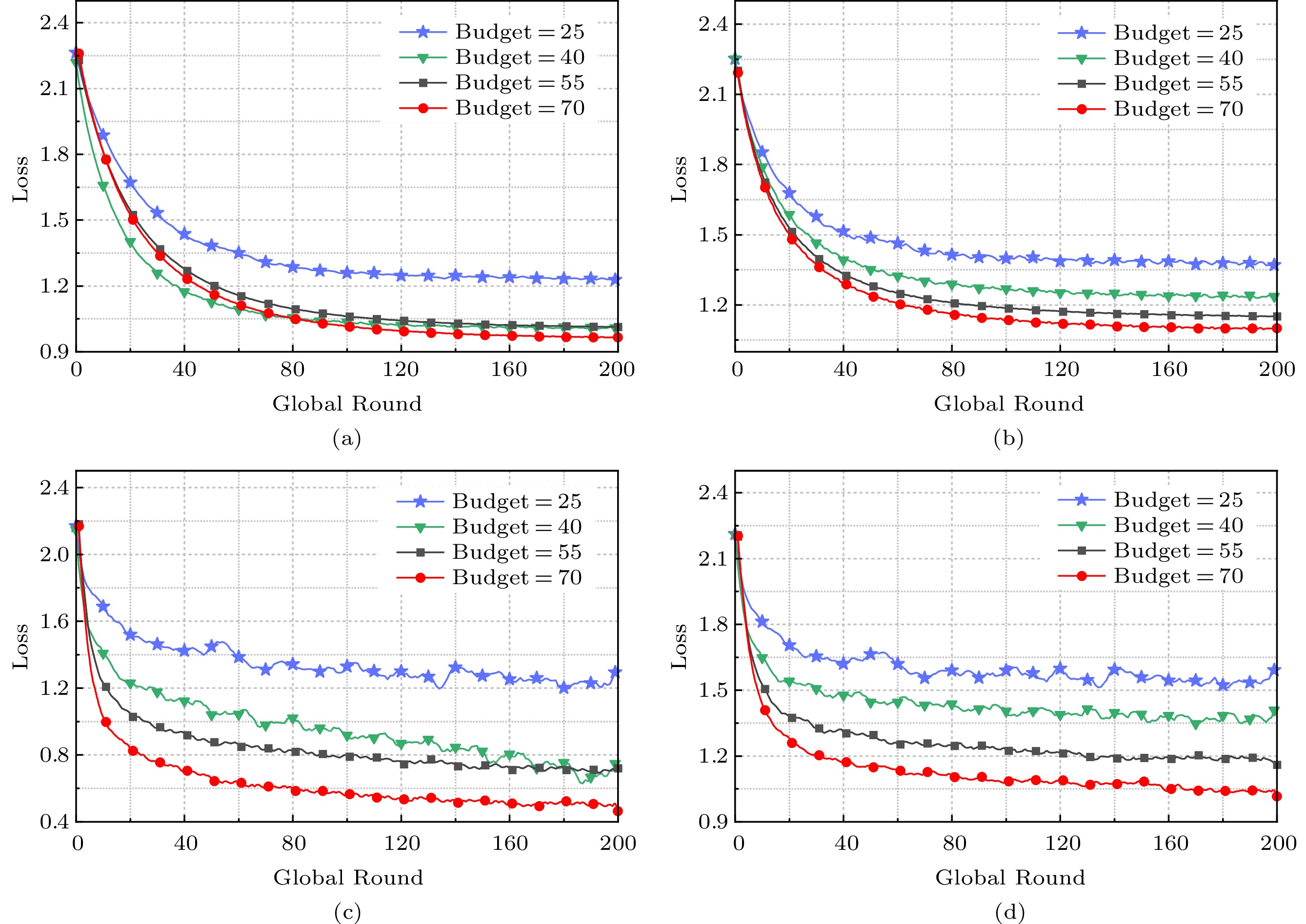
Figure 8. Performance of CNN on FMNIST[19]. (a) Accuracy. (b) Loss.Additionally, we analyze the influence of the server's budget B under different models and datasets, as depicted in Fig.9. By varying the budgets from 25 to 70, we evaluate the loss of WICS by adopting LR and CNN under MNIST and FMNIST, respectively. The results reveal that a larger B value corresponds to a smaller loss of the model. The reason is that a larger budget can allow more clients to update their local datasets in each time slot. That is, the local datasets will be fresher, and the global model will achieve a better learning performance. This observation aligns with the convergence upper bound analysis in Section 3.
![]() Figure 9. Influence of the server's budget on WICS under different datasets[19]. (a) Loss of LR on MNIST. (b) Loss of LR on FMNIST. (c) Loss of CNN on MNIST. (d) Loss of CNN on FMNIST.
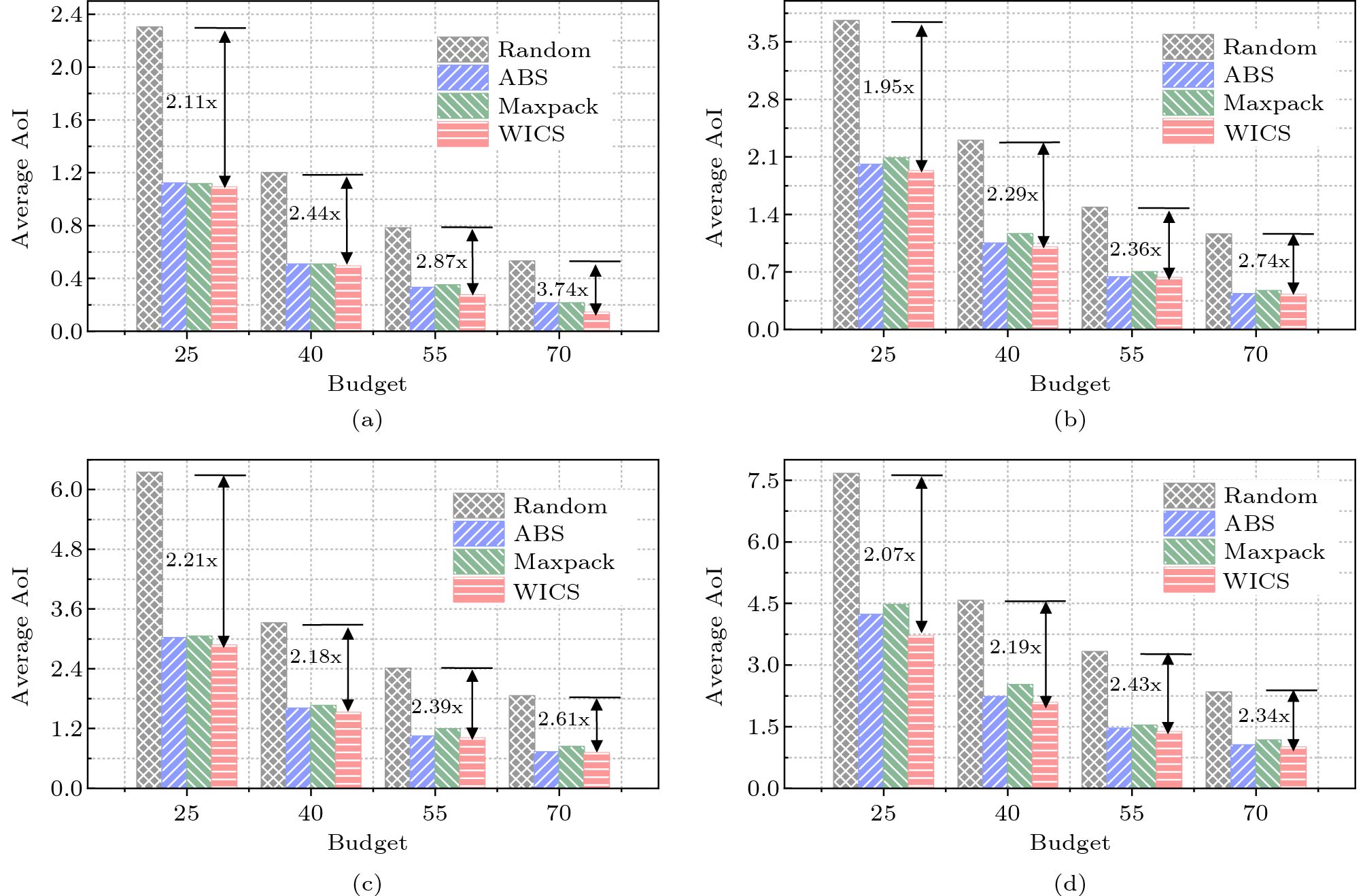
Figure 9. Influence of the server's budget on WICS under different datasets[19]. (a) Loss of LR on MNIST. (b) Loss of LR on FMNIST. (c) Loss of CNN on MNIST. (d) Loss of CNN on FMNIST.Finally, we exhibit the performance of all four algorithms in terms of the average AoI under various number of clients, which can be computed by
\Delta = \frac{1}{TN}\sum_{t=1}^{T}\sum_{i=1}^{N}\frac{n_i}{n}\Delta_i(t). The evaluation results are illustrated in Fig.10, where we change the budget B in the range of [25, 70] and vary the number of clients from 10 to 40. These figures show that our proposed algorithm WICS consistently achieves the lowest weighted average AoI among all the four algorithms. More specifically, the schemes in ABS, MaxPack, and WICS outperform the random algorithm significantly, and the performance of ABS is the closest when compared with WICS. Furthermore, as the number of clients N increases, the weighted average AoI shows an upward trend. This is because when the budget remains constant, the number of clients not selected by the server in each time slot grows with N , leading to the increment of AoI values during each time slot. Consequently, the weighted average AoI increases with rising N . Notably, the findings in Fig.10 align with those in Figs.3-8, which confirms the validity of Assumption 4.
6. Related Work
Client Selection for FL. Research on the client selection problem in FL has been extensive and multifaceted, taking into account various aspects of the system, such as statistical heterogeneity and system heterogeneity. Various optimization objectives, such as importance sampling and resource-aware optimization-based approaches, have been explored[33, 34]. The objective of importance sampling is to reduce the variance in traditional optimization algorithms based on stochastic gradient descent. For example, many existing studies utilize metrics like clients' local gradients or local loss to assess the significance of clients' local data and subsequently select clients based on data importance[35]. Additionally, resource-aware optimization-based work encompasses diverse strategies, including CPU frequency allocation[14], communication bandwidth allocation[36], and straggler-aware client scheduling[37], which target the optimization of various aspects of the federated learning system. However, it is worth noting that the majority of these researches operate under the assumption that clients' local datasets remain static throughout the FL process. In contrast, our research concentrates on the scenario where clients' local data needs to be updated periodically. Although the authors in [19] considered the dynamics of local data, we provide a more rigorous and comprehensive performance analysis.
Age of Information. AoI, a concept originally introduced by [18], is a novel application-layer metric for measuring freshness. Since its inception, there have been a lot of studies dedicated to AoI optimization, covering a wide spectrum of problems. A significant class of problems that has attracted much attention is how to design schedulers to minimize AoI[18, 38–41]. For instance, Kaul et al.[18] developed an analytical model for mobile crowd-learning, which takes into account the intricate interplay between the stochastic arrivals of participating users, information evolutions at points of interest, and reward mechanisms. Xu et al.[42] designed an AoI-guaranteed incentive mechanism to maximize the utilities of the platform and all workers simultaneously. Dai et al.[38] delved into how to minimize the average AoI of sensor nodes in data collection through mobile crowdsensing. The authors in [39] tackled the problem of minimizing AoI in single-hop and multi-hop wireless networks. Fang et al.[40] explored the design of a joint preprocessing and transmission policy to minimize the average AoI at the destination while optimizing energy consumption at IoT devices. Meanwhile, Tang et al.[41] considered the challenge of minimizing AoI while adhering to constraints on both bandwidth and power consumption. Despite this extensive body of work, none of these existing work consider the specific problem of minimizing the average AoI value of local datasets in FL systems.
7. Discussion
In this section, we present various discussions on possible extensions of our proposed algorithm for more practical scenarios and then point out the potential directions for future in-depth research.
First, we discuss a dynamic scenario where clients may join or leave the system dynamically. In the client selection phase, we assume that all clients can continuously participate in the FL system. However, for a multi-client oriented SC system, any client may join or leave anytime online. Consequently, some clients may not participate in the system during certain periods, i.e., the platform cannot select several clients sometimes. Therefore, how to address the dynamic arrival of clients is a critical challenge. This challenge could lead to new potential research directions, such as the selection problem with unavailable arms, which will be investigated in our future work.
Then, we explore the extensions of our algorithm that can adapt to more fine-grained integration of fresh data and stale data. For simplicity, we adopt a coarse-grained setting about datasets, i.e., the selected client will update its whole dataset and omit the effect of stale data. Actually, these chosen clients may still make use of their old data when performing local training. Therefore, we need to consider the integration of fresh data and stale data. For example, we can set a discount factor based on time, which can give more weight to fresh information. Establishing a sophisticated and practical integration method for dynamic datasets is a very complex research issue in itself, which may result in a completely new research work.
Next, we intend to consider different data distributions with WICS to support more realistic applications. In this paper, we consider a typical centralized FL system where data is independent and identically distributed (IID). Actually, the datasets of various clients may be non-IID in real-world applications. If a client only updates data of a certain category, the update may be ineffective. In our future work, we attempt to investigate the influence of non-IID data and the update of non-IID data. In addition, we primarily emphasize the data freshness as a key factor in the client selection, and we will take more practical factors into consideration.
Finally, we plan to enhance the performance of WICS from an experimental perspective. In our simulations, we evaluate the effectiveness of WICS under several datasets and simple models. In order to comprehensively validate the robustness of our algorithm, we will strive to make full use of complex datasets (e.g., CIFAR, ImageNet, and SVHN) to observe the changing trends of model accuracy, loss, and the values of AoI. On the other hand, for tackling more intricate FL tasks, opting for sophisticated model architectures (e.g., RestNet, VGG, and AlexNet) could be instrumental. Nevertheless, some large models may not be suitable for deployment on local weak devices, which will be further studied in our future work.
8. Conclusions
In this paper, we introduced a novel AoI-aware FL system, where clients might use fresh datasets to perform local model training and the server tries to select some clients to provide fresh datasets in each time slot but is constrained by a limited budget. We employed AoI as a metric to quantify dataset freshness and performed a comprehensive theoretical analysis to establish the convergence upper bound for the AoI-aware FL system. Building upon this analysis, we formulated the client selection issue as a restless multi-armed bandit. To effectively address this problem, we proposed the Whittle's-Index-based Client Selection algorithm, called WICS. Moreover, we theoretically proved that WICS can achieve nearly optimal performance on client selection. Extensive simulations on two real-world datasets demonstrated the effectiveness of our proposed algorithm.
-
Figure 2. Example for Algorithm 1 with B=5.
Figure 3. Performance of LR on MNIST[19]. (a) Accuracy. (b) Loss.
Figure 4. Performance of LR on FMNIST[19]. (a) Accuracy. (b) Loss.
Figure 7. Performance of CNN on MNIST[19]. (a) Accuracy. (b) Loss.
Figure 8. Performance of CNN on FMNIST[19]. (a) Accuracy. (b) Loss.
Figure 9. Influence of the server's budget on WICS under different datasets[19]. (a) Loss of LR on MNIST. (b) Loss of LR on FMNIST. (c) Loss of CNN on MNIST. (d) Loss of CNN on FMNIST.
Table 1 Description of Major Notations
Variable Description i,t Index of client and time slot, respectively \mathcal{N},\mathcal{T} Set of clients and time slots, respectively \mathcal{N}_t Set of selected clients in time slot t \mathcal{D}_t^i Local dataset of client i in time slot t F(\boldsymbol\omega) Global loss function with parameter vector \boldsymbol\omega F_{t,\ i}(\boldsymbol\omega) Loss function of client i in time slot t \boldsymbol\omega_0,\boldsymbol\omega^* Initial and optimal model parameter vector \boldsymbol\omega_t,\boldsymbol\omega_t^i Global model parameter vector and local model parameter vector of client i in time slot t, respectively n_i,n Size of client i's local dataset and total size of all clients' local datasets, respectively k,\tau Index and total number of local iterations, respectively \xi_{t}^{i,k} The k-th mini-batch sampled from \mathcal{D}_{t}^{i} \eta_t Learning rate in time slot t \bar{\eta},\widetilde{\eta} Minimum and maximum of the learning rate, respectively p_i Payment of client i for obtaining fresh data B Budget of the server per time slot u_i(t) Latest update time slot of the dataset \mathcal{D}_{t}^{i} \Delta_{i}(t) AoI value of client i in time slot t Algorithm 1. Whittle's Index Based Client Selection (WICS) Input: the set of clients' AoI values \{\Delta_{1}(t),...,\Delta_{N}(t)\}, the set of clients' weights \{\phi_1,...,\phi_N\}, the set of clients' payments \{p_1,...,p_N\}, the budget of the server B; Output: the index set of selected clients \mathcal{N}_{t+1}; 1: for each client i in \mathcal{N} do 2: Calculate its WI value WI_{i,\ t} according to (26) and send WI_{i,\ t} to the server; 3: end for 4: The server sorts the clients into (i_1,i_2,...,i_N) such that WI_{i_1,\ t}\geqslant WI_{i_2,\ t}\geqslant ... \geqslant WI_{i_N,\ t}, and initializes an empty set \mathcal{N}_{t+1} as well as k=1; 5: while k\leqslant N do 6: if \sum_{i \in \mathcal{N}_{t+1}}(p_i+ p_{i_k}) <B then 7: \mathcal{N}_{t+1} \gets \mathcal{N}_{t+1}\cup \{i_k\}; 8: end if 9: k=k+1; 10: end while -
[1] Yang Q, Liu Y, Chen T T, Tong Y X. Federated machine learning: Concept and applications. ACM Trans. Intelligent Systems and Technology, 2019, 10(2): Article No. 12. DOI: 10.1145/3298981.
[2] Li T, Sahu A K, Talwalkar A, Smith V. Federated learning: Challenges, methods, and future directions. IEEE Signal Processing Magazine, 2020, 37(3): 50–60. DOI: 10.1109/MSP.2020.2975749.
[3] Shi Y F, Liu Y Q, Wei K, Shen L, Wang X Q, Tao D C. Make landscape flatter in differentially private federated learning. In Proc. the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2023, pp.24552-24562. DOI: 10.1109/CVPR52729.2023.02352.
[4] Antunes R S, da Costa C A, Küderle A, Yari I A, Eskofier B M. Federated learning for healthcare: Systematic review and architecture proposal. ACM Trans. Intelligent Systems and Technology, 2022, 13(4): Article No. 54. DOI: 10.1145/3501813.
[5] Wang Z B, Huang Y T, Song M K, Wu L B, Xue F, Ren K. Poisoning-assisted property inference attack against federated learning. IEEE Trans. Dependable and Secure Computing, 2023, 20(4): 3328–3340. DOI: 10.1109/TDSC.2022.3196646.
[6] Lim W Y B, Luong N C, Hoang D T, Jiao Y T, Liang Y C, Yang Q, Niyato D, Miao C Y. Federated learning in mobile edge networks: A comprehensive survey. IEEE Communications Surveys & Tutorials, 2020, 22(3): 2031–2063. DOI: 10.1109/COMST.2020.2986024.
[7] Karimireddy S P, Kale S, Mohri M, Reddi S J, Stich S U, Suresh A T. SCAFFOLD: Stochastic controlled averaging for federated learning. In Proc. the 37th International Conference on Machine Learning, Jul. 2020, Article No. 476.
[8] Wu X D, Huang F H, Hu Z M, Huang H. Faster adaptive federated learning. In Proc. the 37th AAAI Conference on Artificial Intelligence, Feb. 2023, pp.10379–10387. DOI: 10.1609/AAAI.V37I9.26235.
[9] Wang H, Kaplan Z, Niu D, Li B C. Optimizing federated learning on Non-IID data with reinforcement learning. In Proc. the 2020 IEEE Conference on Computer Communications (INFOCOM), Jul. 2020, pp.1698–1707. DOI: 10.1109/INFOCOM41043.2020.9155494.
[10] Chen C, Xu H, Wang W, Li B C, Li B, Chen L, Zhang G. Communication-efficient federated learning with adaptive parameter freezing. In Proc. the 41st IEEE International Conference on Distributed Computing Systems (ICDCS), Jul. 2021, pp.1–11. DOI: 10.1109/ICDCS51616.2021.00010.
[11] Wang Z B, Ma J J, Wang X, Hu J H, Qin Z, Ren K. Threats to training: A survey of poisoning attacks and defenses on machine learning systems. ACM Computing Surveys, 2023, 55(7): 134. DOI: 10.1145/3538707.
[12] Zhang X L, Li F T, Zhang Z Y, Li Q, Wang C, Wu J P. Enabling execution assurance of federated learning at untrusted participants. In Proc. the 2020 IEEE Conference on Computer Communications (INFOCOM), Jul. 2020, pp.1877–1886. DOI: 10.1109/INFOCOM41043.2020.9155414.
[13] Yuan X Y, Ma X Y, Zhang L, Fang Y G, Wu D P. Beyond class-level privacy leakage: Breaking record-level privacy in federated learning. IEEE Internet of Things Journal, 2022, 9(4): 2555–2565. DOI: 10.1109/JIOT.2021.3089 713.
[14] Tran N H, Bao W, Zomaya A, Nguyen M N H, Hong C S. Federated learning over wireless networks: Optimization model design and analysis. In Proc. the 2019 IEEE Conference on Computer Communications (INFOCOM), Apr. 2019, pp.1387–1395. DOI: 10.1109/INFOCOM.2019.8737464.
[15] Wang Z L, Hu Q, Li R N, Xu M H, Xiong Z H. Incentive mechanism design for joint resource allocation in blockchain-based federated learning. IEEE Trans. Parallel and Distributed Systems, 2023, 34(5): 1536–1547. DOI: 10.1109/TPDS.2023.3253604.
[16] Zhan Y F, Li P, Qu Z H, Zeng D Z, Guo S. A learning-based incentive mechanism for federated learning. IEEE Internet of Things Journal, 2020, 7(7): 6360–6368. DOI: 10.1109/JIOT.2020.2967772.
[17] Zeng R F, Zhang S X, Wang J Q, Chu X W. FMore: An incentive scheme of multi-dimensional auction for federated learning in MEC. In Proc. the 40th IEEE International Conference on Distributed Computing Systems (ICDCS), Nov. 29–Dec. 1, 2020, pp.278–288. DOI: 10.1109/ICDCS47774.2020.00094.
[18] Kaul S, Gruteser M, Rai V, Kenney J. Minimizing age of information in vehicular networks. In Proc. the 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Jun. 2011, pp.350–358. DOI: 10.1109/SAHCN.2011.5984917.
[19] Wu C, Xiao M J, Wu J, Xu Y, Zhou J R, Sun H. Towards federated learning on fresh datasets. In Proc. the 20th IEEE International Conference on Mobile Ad Hoc and Smart Systems (MASS), Sept. 2023, pp.320–328. DOI: 10.1109/MASS58611.2023.00046.
[20] Xu Y, Xiao M J, Wu J, Tan H S, Gao G J. A personalized privacy preserving mechanism for crowdsourced federated learning. IEEE Trans. Mobile Computing, 2024, 23(2): 1568–1585. DOI: 10.1109/TMC.2023.3237636.
[21] Zhou Y P, Liu X Z, Fu Y, Wu D, Wang J H, Yu S. Optimizing the numbers of queries and replies in convex federated learning with differential privacy. IEEE Trans. Dependable and Secure Computing, 2023, 20(6): 4823–4837. DOI: 10.1109/TDSC.2023.3234599.
[22] Hosmer D W, Lemeshow S. Applied Logistic Regression (2nd edition). Wiley, 2000. DOI: 10.1002/0471722146.
[23] Hearst M A, Dumais S T, Osuna E, Platt J, Scholkopf B. Support vector machines. IEEE Intelligent Systems and their Applications, 1998, 13(4): 18–28. DOI: 10.1109/5254.708428.
[24] Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 2017, 60(6): 84–90. DOI: 10.1145/3065386.
[25] McCall B P. Multi-armed bandit allocation indices (J. C. Gittins). SIAM Review, 1991, 33(1): 154–155. DOI: 10.1137/1033039.
[26] Xu Y, Xiao M J, Wu J, Zhang S, Gao G J. Incentive mechanism for spatial crowdsourcing with unknown social-aware workers: A three-stage stackelberg game approach. IEEE Trans. Mobile Computing, 2023, 22(8): 4698–4713. DOI: 10.1109/TMC.2022.3157687.
[27] Whittle P. Restless bandits: Activity allocation in a changing world. Journal of Applied Probability, 1988, 25(A): 287–298. DOI: 10.2307/3214163.
[28] LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278–2324. DOI: 10.1109/5.726791.
[29] Xiao H, Rasul K, Vollgraf R. Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms. arXiv: 1708.07747, 2017. http://arxiv.org/abs/1708.07747, May 2024.
[30] Wang S Q, Tuor T, Salonidis T, Leung K K, Makaya C, He T, Chan K. When edge meets learning: Adaptive control for resource-constrained distributed machine learning. In Proc. the 2018 IEEE Conference on Computer Communications (INFOCOM), Apr. 2018, pp.63–71. DOI: 10.1109/INFOCOM.2018.8486403.
[31] Yang H H, Arafa A, Quek T Q S, Poor H V. Age-based scheduling policy for federated learning in mobile edge networks. In Proc. the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), May 2020, pp.8743–8747. DOI: 10.1109/ICASSP40776.2020.9053740.
[32] Yang K, Jiang T, Shi Y M, Ding Z. Federated learning via over-the-air computation. IEEE Trans. Wireless Communications, 2020, 19(3): 2022–2035. DOI: 10.1109/TWC.2019.2961673.
[33] Wang E, Zhang M J, Yang B, Yang Y J, Wu J. Large-scale spatiotemporal fracture data completion in sparse crowdSensing. IEEE Trans. Mobile Computing, 2023. DOI: 10.1109/TMC.2023.3339089.
[34] Wang Z B, Hu J H, Lv R Z, Wei J, Wang Q, Yang D J, Qi H R. Personalized privacy-preserving task allocation for mobile crowdsensing. IEEE Trans. Mobile Computing, 2019, 18(6): 1330–1341. DOI: 10.1109/TMC.2018.2861393.
[35] Lai F, Zhu X F, Madhyastha H V, Chowdhury M. Oort: Efficient federated learning via guided participant selection. In Proc. the 15th USENIX Symposium on Operating Systems Design and Implementation (OSDI), 2021, pp.19–35.
[36] Xu Y, Xiao M J, Tan H S, Liu A, Gao G J, Yan Z Y. Incentive mechanism for differentially private federated learning in industrial internet of things. IEEE Trans. Industrial Informatics, 2022, 18(10): 6927–6939. DOI: 10.1109/TII.2021.3134257.
[37] Lee H, Lee J, Kim H, Pack S. Straggler-aware in-network aggregation for accelerating distributed deep learning. IEEE Trans. Services Computing, 2023, 16(6): 4198–4204. DOI: 10.1109/TSC.2023.3309318.
[38] Dai Z P, Wang H, Liu C H, Han R, Tang J, Wang G R. Mobile crowdsensing for data freshness: A deep reinforcement learning approach. In Proc. the 2021 IEEE Conference on Computer Communications (INFOCOM), May 2021. DOI: 10.1109/INFOCOM42981.2021.9488791.
[39] Tripathi V, Modiano E. Age debt: A general framework for minimizing age of information. In Proc. the 2021 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), May 2021. DOI: 10.1109/INFOCOMWKSHPS51825.2021.9484621.
[40] Fang M B, Wang X J, Xu C, Yang H H, Quek T Q S. Computing-aided update for information freshness in the internet of things. In Proc. the 2021 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), May 2021. DOI: 10.1109/INFOCOMWKSHPS51825.2021.9484521.
[41] Tang H Y, Wang J T, Song L Q, Song J. Minimizing age of information with power constraints: Multi-user opportunistic scheduling in multi-state time-varying channels. IEEE Journal on Selected Areas in Communications, 2020, 38(5): 854–868. DOI: 10.1109/JSAC.2020.2980911.
[42] Xu Y, Xiao M J, Zhu Y, Wu J, Zhang S, Zhou J R. Aoi-guaranteed incentive mechanism for mobile crowdsensing with freshness concerns. IEEE Trans. Mobile Computing, 2024, 23(5): 4107–4125. DOI: 10.1109/TMC.2023.3285779.
-
其他相关附件
-
本文附件外链
https://rdcu.be/dODHA -
DOCX格式
3914-Chinese Information 点击下载(47KB) -
PDF格式
2024-3-7-3914-Highlights 点击下载(162KB) -
压缩文件
2024-3-7-3914-Highlights 点击下载(68KB)
-




 下载:
下载: