1.   Introduction

With the development of the Internet of Things (IoT)^[1], social networks^[2-4], and E-commerce, distributed stream processing engines (DSPEs) such as Apache Storm ¹ (storm for short) and Apache Flink ² (Flink for short) have attracted much attention from both academia and industry, e.g., Twitter^[2] and Alibaba ³. Compared with batch processing, stream processing offers timely and continuous task processing, which is critical in many real-time applications such as IoT-based monitoring.

Task management is an essential part of a DSPE. The task management module in a DSPE is responsible for task deployment, task selection, and migration in case of node failure or new node addition. Task management directly affects the system throughput and processing delay, which are important indicators to measure the overall performance and the Quality of Service (QoS) of applications. Generally, the QoS of applications refers to the response time, usually in terms of seconds. The task management modules employed in popular DSPEs, including Storm and Flink, adopt an offline scheme. However, in many real-time applications, e.g., IoT-based monitoring, the data and workloads are time-varying, making the static task deployment no longer efficient as the workload changes. As a result, it has been an urgent need to develop an online task management scheme for DSPEs.

Online task management needs to support task selection and migration between nodes at runtime while maintaining high performance and QoS. For example, supposing that the task deployment in Storm is to be changed after Storm deploys tasks, all running processes have to be stopped, waiting for all tuples (the processing units in Storm) to be completed so that Storm can perform task migration. This procedure lasts about 30 seconds^[5]. Some prior studies, such as T-Storm^[6] and TS-Storm^[7], proposed to improve the task management scheme of Storm. But they still take over 10 seconds of system stall during a task migration, which cannot meet the QoS requirements of real-time stream-processing applications. We find that the intrinsic reason for the high system stall time during a task migration in Storm, T-Storm, and TS-Storm is that the tasks are tightly coupled with resources in a task deployment. More specifically, tasks (implemented as threads/Executors) and resources in Storm are tightly coupled in Workers, which are implemented as Java Virtual Machine (JVM) processes. In Storm, processes are the smallest units for task deployments and migrations. In other words, Storm uses a process-level scheme for task deployments and migrations. Therefore, when a task migration is started, all tasks within a Worker have to be stopped so that the system can reallocate the Worker’s resources to tasks. In such a scheme, many Workers might even be stopped due to a small-scaled task migration involving a small number of tasks.

In this paper, to overcome the problem of offline task management in Storm, T-Storm, and TS-Storm, and to offer an efficient online task management mechanism for DSPEs, we propose N-Storm (Nonstop Storm). The main idea of N-Storm is to decouple tasks from resources during task deployments and migrations. In addition, instead of the process-level task migration in Storm, N-Storm adopts a new thread-level scheme. As a consequence, N-Storm can perform thread-level task migrations at runtime without affecting other tasks. Further, based on N-Storm, we propose an online task deployment algorithm called Online Task Deployment (OTD). Instead of previous task deployment algorithms^[6-8] that have to stop the system for a while during a task re-deployment, OTD can avoid system stall by gradually adjusting the old task deployment to a new one that is more efficient for the current workload. Briefly, we make the following contributions in this study.

● We find out the intrinsic cause of the inefficiency of task migrations in DSPEs like Apache Storm, i.e., the coupling of tasks and resources. Motivated by this finding, we propose N-Storm, which supports online task migrations. N-Storm has two new designs. First, it presents a task-resource decoupling architecture for DSPEs. Second, it uses a thread-level scheme to manage tasks rather than the process-level method in Storm. We also propose two optimization strategies, namely, lazy task killing and synchronization cycle adjustment, to further improve the performance of N-Storm.

● Based on N-Storm, we further propose OTD for realizing online task deployments. OTD can support task deployments and migrations at runtime. OTD is implemented by gradually adjusting the current task allocation plan to a new optimized one according to the network communication cost and the runtime states of resources. With this mechanism, we need not stop the system during a task deployment. We demonstrate that OTD can adapt to different kinds of applications, including computation- and communication-intensive applications.

● We verify the effectiveness and efficiency of N-Storm and OTD on a real DSPE cluster. The experimental results show that N-Storm can avoid the stop time and save up to 87% of the severe performance degradation time compared with Storm and other state-of-the-art approaches. Furthermore, OTD can increase average CPU usage by 51% for computation-intensive applications and reduce network communication costs by 88% for communication-intensive applications.

The remaining of the paper is structured as follows. Section 2 introduces the background and motivation of our research. Section 3 describes the design and implementation of N-Storm in detail. Section 4 presents OTD in detail. Section 5 reports the experimental results. Section 6 discusses related work. Finally, Section 7 concludes the paper.

2.   Background and Motivation

2.1   Basic Concepts of DSPEs

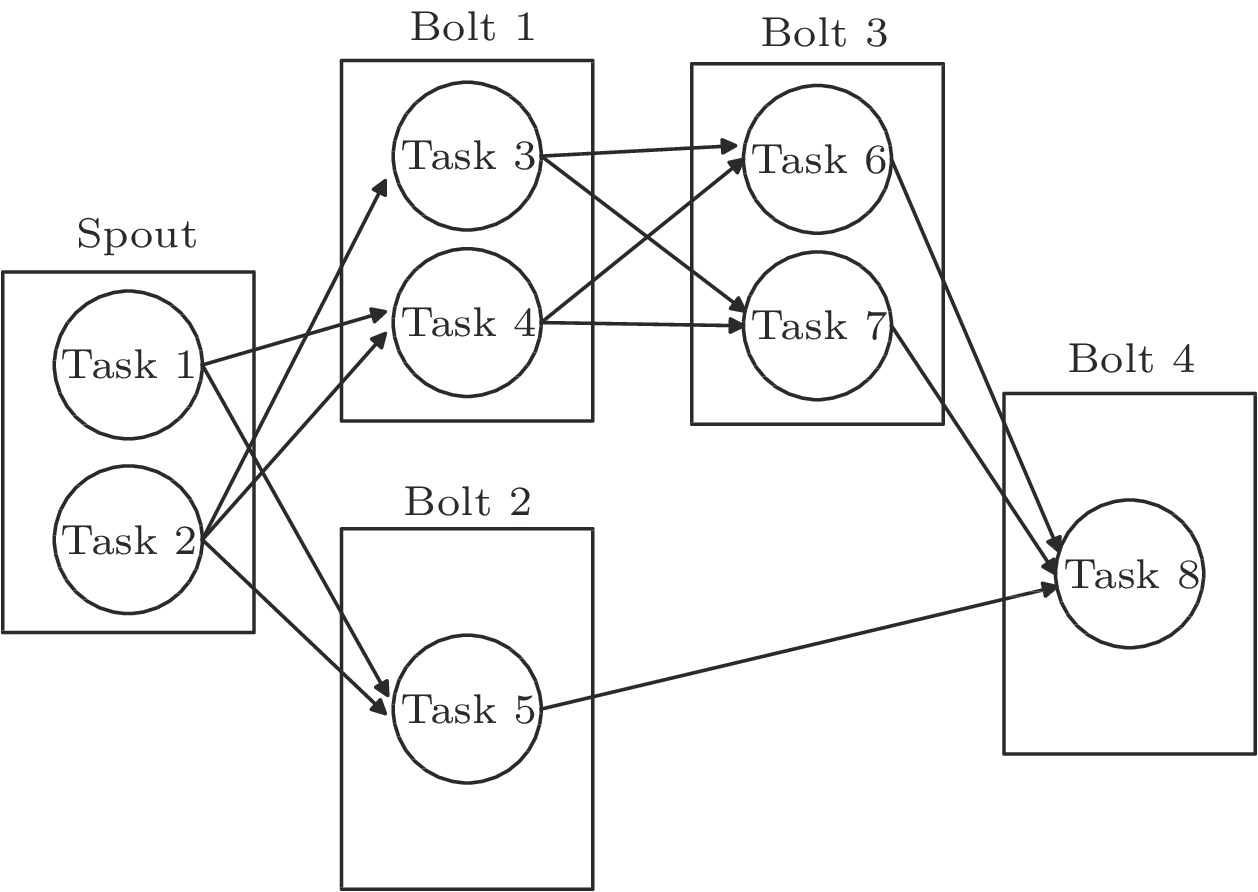
Storm packages the logic of a stream processing application as a ``Topology'', an abstraction of Storm tasks, represented as a directed acyclic graph (DAG), as shown in Fig.1. Each vertex in a Topology represents a logical operator. There are two types of vertices in a Topology, namely Spout and Bolt. The Spout is responsible for receiving data tuples from the data source. The Bolt is responsible for encapsulating the processing logic and processing specific tuples. Thus, Storm can start multiple tasks to perform the processing logic of a vertex in parallel.

Figure  1.  Example of the Storm Topology.

下载: 全尺寸图片 幻灯片

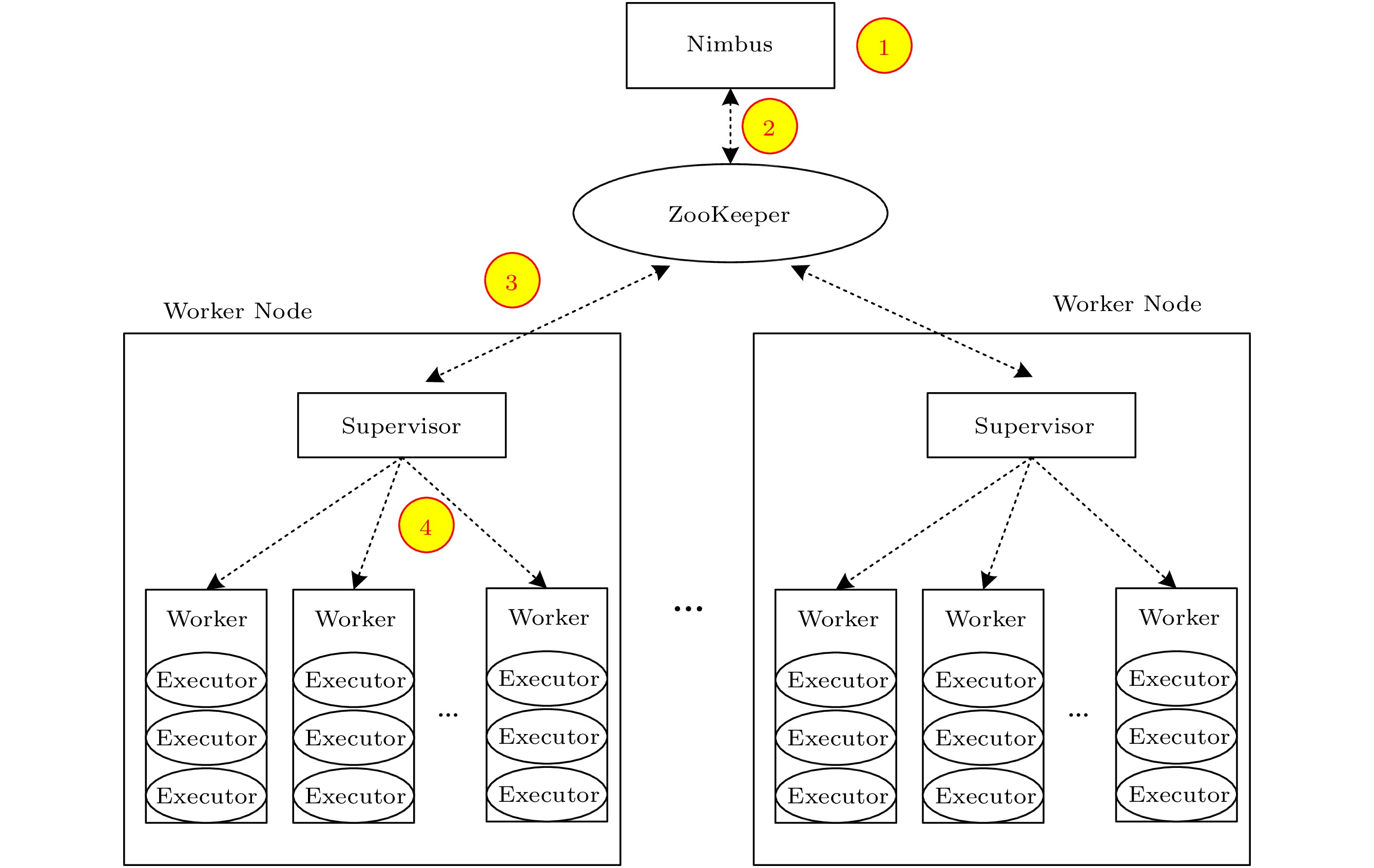
Generally, Storm runs on a cluster with the master-slave architecture, as shown in Fig.2. The master node in Storm is called Nimbus. It is responsible for conducting task deployments and monitoring the running state of Storm. Other nodes in the cluster are called Worker nodes. A Worker node is responsible for accepting, running, and managing tasks assigned by Nimbus. A Worker node consists of a Supervisor process and some Worker processes (denoted as Workers in the texts below). The Supervisor in a Worker node communicates with the Nimbus through the Apache ZooKeeper ⁴, which is a distributed coordinator. A Worker is a JVM process that runs on a Worker node with configured resources. Each Worker can have one or more Executors. An Executor is a thread for processing one specific task, which refers to a part of the particular work of a vertex. In this paper, an Executor can be considered as a task.

Figure  2.  Architecture and task management mechanism of Storm.

下载: 全尺寸图片 幻灯片

In Storm, all processes, including Nimbus, Supervisors, and Workers, do not maintain their runtime states inside themselves. More specifically, all states are stored on ZooKeeper, meaning that all modules in Storm (i.e., Nimbus, Supervisors, and Workers) are stateless^[2]. Thus, when a process is killed, it simply restarts and gets messages from ZooKeeper without affecting the whole system. Note that our work is also based on the stateless principle of Storm.

Fig.2 shows the task management mechanism in Storm. It includes four steps. First, Nimbus generates an allocation plan for the given Topology by a task deployment algorithm. Second, Nimbus writes the allocation plan into ZooKeeper. Third, the Supervisor on each Worker node gets the allocation plan from the ZooKeeper. Finally, each Supervisor checks its Workers, where some tasks have changed, and restarts these Workers.

2.2   Limitations of Current Task Management

The task management in a DSPE is designed to solve the following two problems.

Problem 1: Task Deployment. Given all tasks, resources, and the distribution of the resources among the Worker nodes, how to find an optimal scheme to deploy all tasks to Workers?

Problem 2: Task Migration. In case of removing or adding a Worker node, or updating the task deployment, how to migrate tasks to other Worker nodes?

Note that an offline task management mechanism only deals with task deployments, while an online task management mechanism tackles not only task deployments but also task migrations.

Offline solutions are inefficient for many stream processing applications because the data and workloads are time-varying. The inefficiency can be interpreted for two reasons. First, the throughput of a data flow may fluctuate with time. For example, prior work^[9] showed that the data flow in a log-monitoring application would increase sharply when some bugs happened. Second, some logical operators in the Storm Topology will use non-random partitioning strategies, such as region-based or hash-based partitioning, making the data distribution uneven in the system^[10]. Thus, loads of the tasks belonging to the same logical operator (i.e., the Bolt) are different. Consequently, Storm calls for online schemes that can change the task deployment at runtime.

However, online task deployments cannot be supported by trivially extending existing DSPEs. For example, Storm uses the rebalance command to update the task deployment. This command needs first to stop all running Executors that belong to the Topology and kill all Workers. After that, Nimbus generates a new allocation plan and restarts Topology according to the new allocation plan. With such a scheme, the system needs to wait until all tuples in the queue are finished. To make it worse, Nimbus and Supervisors have to wait a threshold of 30 seconds for confirming the completion states of tasks, meaning that the rebalance command will make the system stop for at least 30 seconds.

Instead of stopping the running of the entire Topology, a better way is to send the new allocation plan to the Supervisor at each Worker node and let the Supervisor perform task migrations. Such a scheme was proposed in T-Storm^[6] and TS-Storm^[7]. With this scheme, the Supervisor can selectively kill and restart the Workers whose Executors need to be updated so that the running of other Workers will not be interrupted. This approach is more efficient than the ``rebalance'' command. However, it still has to stop the system for more than 10 seconds when performing a task migration^[5], mainly because stopping a Worker means killing all the Executors within the Worker. Thus, the system's stop will incur much waiting and executing time, especially when only a few Executors within the Worker need to be updated.

Through a deep investigation on the implementation of existing DSPEs, we find the intrinsic reason for the high system-stall time during a task migration in Storm, T-Storm, and TS-Storm is that the tasks are tightly coupled with resources in a task deployment. More specifically, tasks (Executors) and resources are tightly coupled in Workers. With this mechanism, the finest granularity components allowed to be migrated at runtime are process-level components. As a result, a task migration involving a small number of tasks may also cause the stop of many Workers. Therefore, to reduce the cost of task migrations, the architecture of a DSPE needs to be redesigned.

3.   N-Storm: Online Nonstop Task Migration

In this section, we aim to solve problem 2 defined in Subsection 2.2. In particular, we propose a new scheme for online task migrations called N-Storm (Nonstop Storm).

3.1   Main Ideas of N-Storm

We propose two novel techniques for N-Storm: 1) the decoupling of tasks and resources and 2) thread-level task management.

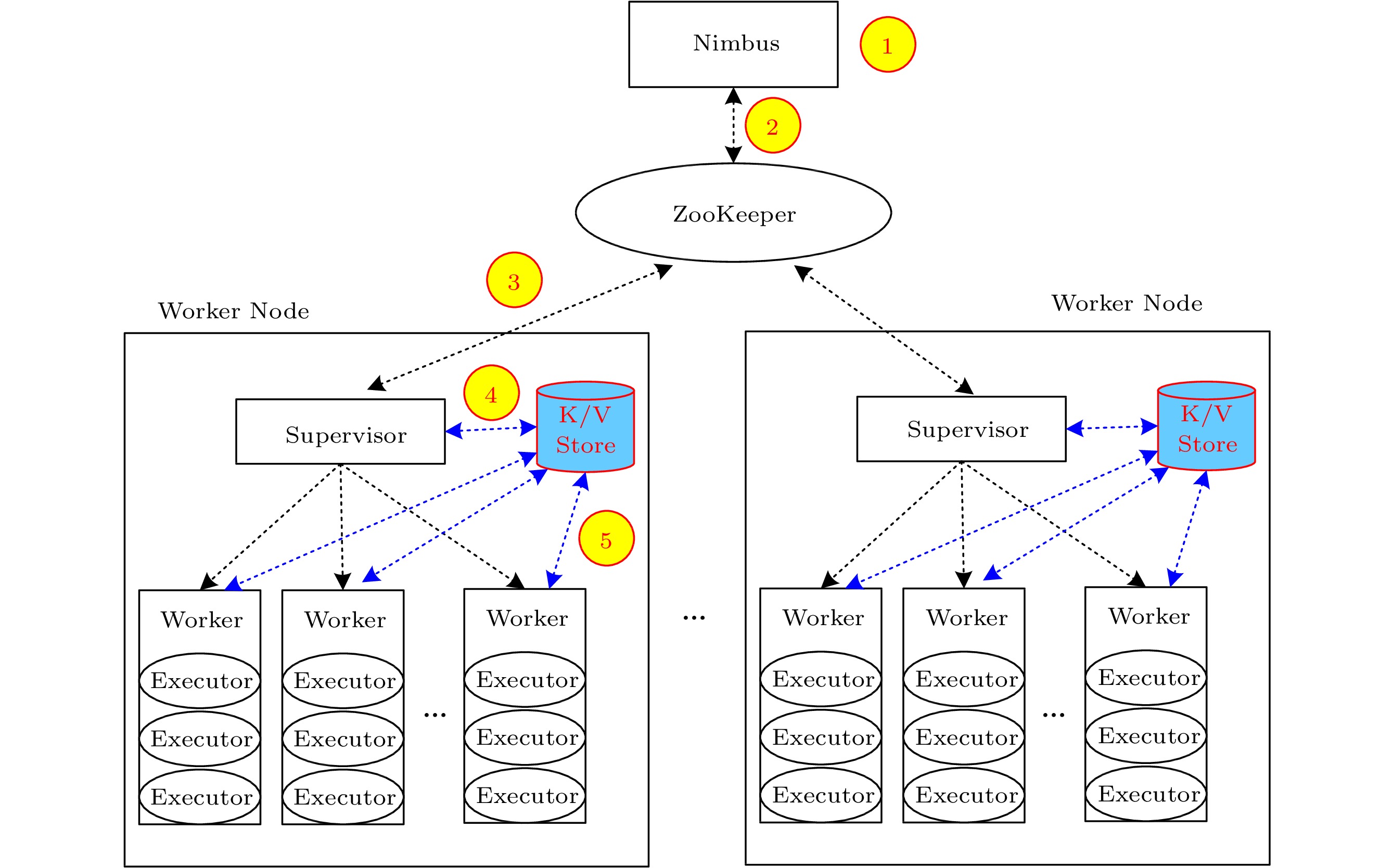
Decoupling of Tasks and Resources. In Storm, tasks are tightly coupled with resources. Notably, a Worker’s key information including tasks, message queues, and resource configurations is stored in an immutable data structure maintained by ZooKeeper. This means the task-resource allocation cannot be changed if tasks have been deployed to Workers. We propose in N-Storm a new scheme to decouple tasks from resources. Specially, we add a new shared updatable data structure in each Worker node to store all configuration information about the task deployment in Workers. This data structure is shared by the Supervisor and all the Workers in a Worker node. The Supervisor can periodically write messages into the data structure to indicate the changes in the allocation plan. At the same time, each Worker in a Worker node can access the shared data structure to get the up-to-date allocation plan, i.e., each Worker can know the change of the current task deployment at runtime from the shared data structure. With this mechanism, we can implement the decoupling of tasks and resources. Here, the main difference between N-Storm and Storm is that N-Storm allows the stop/restart of a specific Executor while Storm does not.

In the implementation of N-Storm, we use a local shared K/V (key/value) store in each node to maintain the shared data structure of the node. The task management mechanism of N-Storm is shown in Fig.3. The first three steps in Fig.3 are the same as those in Fig.2. In the fourth step, the Supervisor on a Worker node periodically writes messages to the K/V store. Finally, in the fifth step, each Worker periodically accesses the K/V store to get the latest message and update the Executors it manages. Based on such implementation, we realize the decoupling of tasks and resources in N-Storm.

Figure  3.  Architecture and task management mechanism of N-Storm. The black dotted arrow is the original control flow of Apache Storm, and the blue dotted arrow is the new control flow of N-Storm.

下载: 全尺寸图片 幻灯片

Thread-Level Task Management. Another idea of N-Storm is to perform task deployments and migrations in terms of threads. As Executors are implemented as threads in Storm, we allow N-Storm to manage each Executor to execute the task management. More specifically, each Worker can directly control its Executors, either for task deployments or task migrations. For example, when the Supervisor informs a Worker through the K/V store to stop an Executor, it can directly kill the thread of the Executor but does not interfere with other Executors within the Worker. Thus, we can adjust the task deployment while keeping all Workers running, avoiding the overhead of the system stop caused by previous DSPEs like Storm, T-Storm, and TS-Storm.

3.2   Implementation of N-Storm

Supervisor. In N-Storm, the Supervisor on a Worker node periodically synchronizes with ZooKeeper to get the latest allocation plan. Differing from Storm, the Supervisors in N-Storm do not need to compare the new allocation plan with the current task deployment. Instead, after requesting messages from ZooKeeper, the Supervisors in N-Storm extract the local allocation plan from the global allocation plan and write it to the K/V store of each Worker node.

Worker. In Storm, after a Worker starts up, the configurations about Executors and the mapping from Executors to message queues are saved in an immutable map structure. In N-Storm, we support atomic updates of these configurations. Thus, Workers periodically access the K/V store to know the changes in the allocation plan and update their configurations. Once a Worker finds that the allocation plan has changed, it can kill/start the tasks involved to deploy tasks adaptive to the changes.

K/V Store. N-Storm extends each Worker node with a lightweight, durable, and atomic K/V store. Both Supervisors and Workers with the same Worker node can access the K/V store within the node simultaneously to communicate with each other. The K/V store handles updates in an append-only mode. It maintains a version number for each record, and read requests will only access the latest version of the record. The K/V store only locks write operations so that read operations can be executed concurrently. Such a scheme does not affect the system performance because only the Supervisor, unique on each Worker node, has the authority to update the allocation plan.

The K/V store only introduces low overhead. Since the K/V store is embedded in each Worker node, no inter-process communication costs will be caused. In addition, write operations will incur disk I/Os but read operations only access the latest version of the K/V records; thus, we can assume that most reads will hit the operating system’s page cache. What is more, a Worker node does not save the global allocation plan but only the local allocation plan, meaning that the size of the K/V store is independent of the cluster size and will not consume too much space. In our implementation, the space cost of a local allocation plan is typically less than 512 bytes.

3.3   Lazy Task Killing

During task migrations, the Executors to be killed may be processing tuples, and there may be tuples in the message queue that are going to be processed by these Executors. If the Executors are killed immediately, all of these associated tuples will be lost. In this case, Storm will reprocess these tuples according to a lineage-based fault-tolerant mechanism^[2], eventually impacting the system’s performance.

Aiming to avoid the tuple loss during task migrations, we propose to delay the killing of Executors. Specifically, when we need to kill an Executor, we do not kill it immediately but let a timer thread in the Worker monitor and perform the killing operation. The timer thread will wait a few seconds before it finally kills the Executor. During the delayed time, two identical Executors may exist in two Workers, but it will not affect the normal execution of the system. This is because upstream Executors can only know one specific downstream Executor at any time. During the delayed time, the old Executor continues to process tuples in the message queue before the timer thread performs the killing, effectively reducing message loss in the old Executor. Note that there is still a tiny chance of losing some intermediate data. However, even when message loss occurs, N-Storm adopts a similar lineage-based fault tolerance mechanism^[2] as Storm to enable all lost messages to be reprocessed after timeouts to ensure data integrity.

3.4   Synchronization Cycle Adjustment

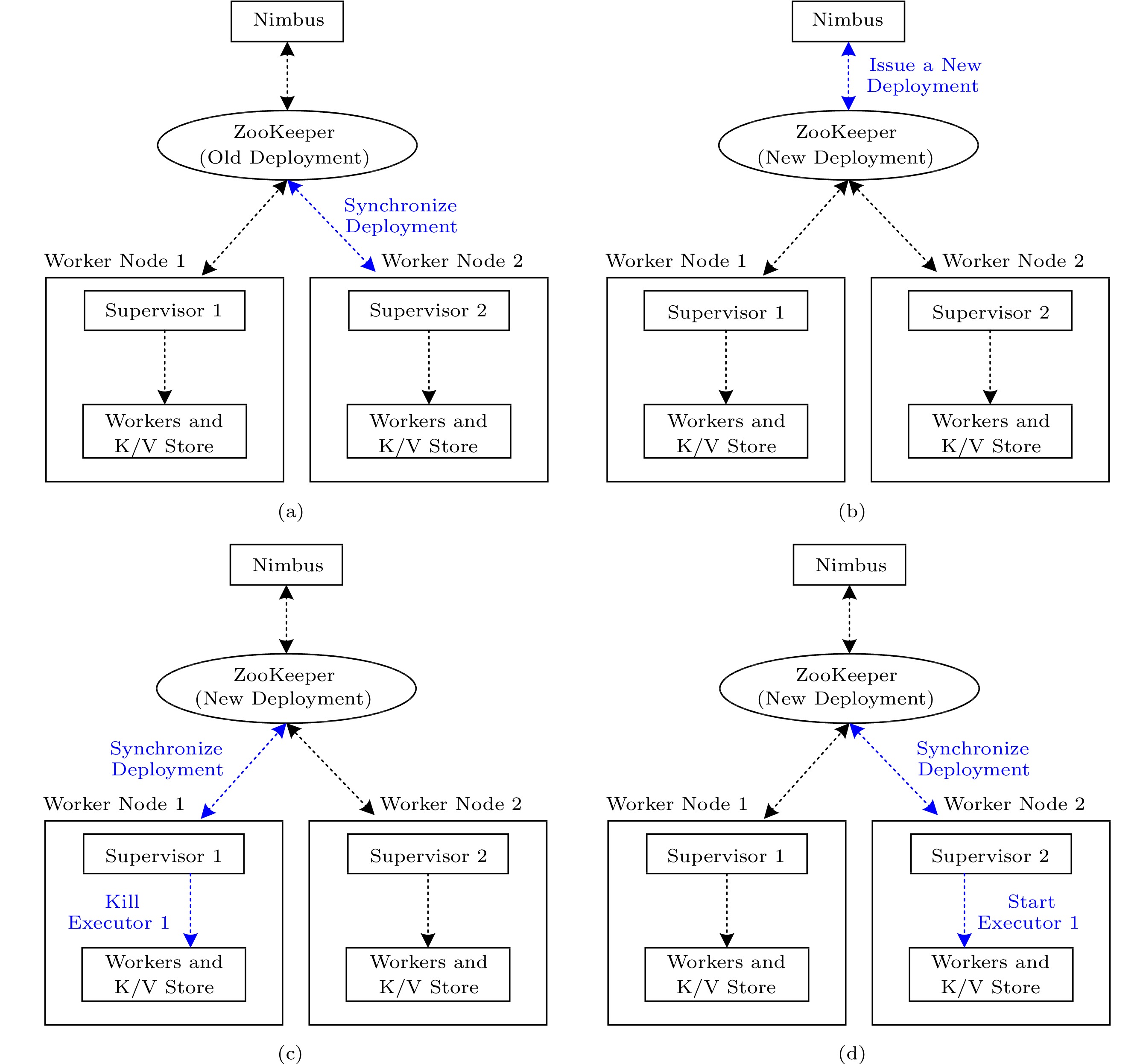
The performance of N-Storm is highly affected by two synchronization cycles. The first is for a Supervisor to communicate with ZooKeeper (Supervisor-ZooKeeper cycle), and the second is for a Worker to visit the K/V store (Worker-Store cycle). Note that Supervisors and Workers work asynchronously in N-Storm. We illustrate the performance impact of this asynchronism in Fig.4. Let us assume that the Supervisor-ZooKeeper cycle is 10 seconds (default set in Storm). We want to migrate Executor 1 from Worker node 1 to Worker node 2. In the worst case, Supervisor 2 visits ZooKeeper at the moment T = 0 and finds that the allocation plan has not changed. Then, after half a second, Nimbus issues a new allocation plan to ZooKeeper. After another half a second, Supervisor 1 accesses ZooKeeper and updates the tasks for Worker node 1, and kills Executor 1. However, Supervisor 2 has to wait until T = 10 s to get the new allocation plan and start the new Executor 1, making Executor 1 stop working for about 9 seconds. Consequently, in the worst case, the stopping time of the migrated Executor is nearly the Supervisor-ZooKeeper cycle. The influence of the Worker-Store cycle is similar.

Figure  4.  Worst case of the asynchronous working mechanism. (a) T = 0 s. (b) T = 0.5 s. (c) T = 1 s. (d) T = 10 s.

下载: 全尺寸图片 幻灯片

Thus, we propose to shorten the Supervisor-ZooKeeper cycle as well as the Worker-Store cycle. Generally, when the cycles are set to a small value, the expected stopping time of migrated Executors can be reduced to improve the overall performance of task migrations. However, a small cycle may also lead to the frequent invoking of the synchronization operation, introducing more CPU costs and increasing the workloads of Supervisors and Workers. In Subsection 5.2, we test the influence of the setting of the cycles on the performance of N-Storm and find that setting a moderate size for the cycles can get the best performance.

3.5   Reliability of N-Storm

N-Storm provides the same reliability as Apache Storm. First, in Storm, modules are stateless, and the states are kept in ZooKeeper, which allows any module to be shut down and restarted at any time^[2]. Thus, the system can continue processing tuples normally after the module is restarted. N-Storm continues to follow the stateless module design. The key idea is that the allocation plan has been persistently stored in the K/V store. Second, Storm uses a lineage-based approach to avoid message loss by having an Acker in the system that tracks tuple processing^[2]. If a tuple times out, it will be reprocessed by the system. Our lazy task-killing mechanism has greatly reduced the likelihood of message loss due to migration, and the Acker can guarantee that no tuple is lost even in the worst case. Third, some applications need to save intermediate processing states. The Storm has not provided persistence support for intermediate states; therefore, some states may be missing during the task migration. Users can save intermediate states using other persistent applications to ensure the reliability of intermediate states.

4.   OTD: Online Task Deployment

This section mainly aims to solve problem 1 defined in Subsection 2.2, which is the task deployment problem. Previous online task deployment schemes^{[6, 7, 11]} deploy all tasks at once, which have to stop the system for seconds, resulting in decreased system throughput. Differing from prior work, we propose an online nonstop task deployment scheme called Online Task Deployment (OTD). Our method can avoid system stall by gradually adjusting the task deployment to make it more efficient for the current workload.

4.1   Problem Analysis

The performance of task deployment is mainly determined by two indicators, namely the processing delay and system throughput. To improve these two indicators, task deployments need to realize the following two objectives.

Objective 1: ensuring that tasks allocated to all resources do not exceed the computation power of the Workers, a.k.a., Workers cannot be overloaded.

Objective 2: minimizing the cost of the network communication between nodes.

A Topology (i.e., a DAG) can be divided into multiple processing paths, and each tuple completes a processing path. Assuming that the complete processing path for a tuple contains tasks ${t}_{1},{t}_{2},\ldots ,{t}_{m}$, the processing delay for each task ${t}_{i}$ is ${Proc}_{i}$, the transmission delay between tasks ${t}_{i}$ and ${t}_{i+1}$ is ${Trans}_{i}$, the overall delay of a processing path can be represented by (1).

Here, ${Proc}_{i}$ mainly involves CPU processing time, memory and cache accessing time, and waiting time. Let us assume that all resources are with identical CPUs, memories, and other hardware. The CPU processing time and memory/cache accessing time can be regarded as constants. The waiting time refers to the time of the tuples in the queue waiting to be processed. When the total number of tasks undertaken by a resource exceeds the computation power of the resources, we can say that the processing speed of the tasks on the resource is slower than the input speed of the data flow. In this case, tuples will accumulate in the queue, and the tuples' waiting time will increase quickly.

Assuming that the network transmission delay between any two nodes is constant (denoted as ${TD}_{N}$), the inter-process transmission delay within nodes is also constant (denoted as ${TD}_{P}$), and a total of k network transmissions are required for processing one tuple, we have the following (2).

Since the cost of network transmissions is much higher than that of inter-process communications, i.e., ${TD}_{N}\gg {TD}_{P}$, we can infer that $\sum _{1\leqslant i\leqslant m-1}{Trans}_{i}$ is proportional to k. Generally, we can assume that the waiting time is short. Therefore, we can say that most of the processing delay is caused by network transmissions.

The maximum throughput of a DSPE is up to the busiest component. It can be a Worker or a network between two nodes. Assuming that a DSPE is deployed on N Worker nodes that contain W Workers, the maximum throughput of the DSPE can be expressed by (3).

Here, ${CC}_{n\to {n}'}$ represents the communication cost between Worker nodes n and $n'$, and ${PC}_{w}$ is the processing cost of Worker w. The symbols $\alpha$ and $\beta$ are two coefficients, which are correlated to the network bandwidth and the computation power of Workers.

The applications running in DSPEs can be roughly divided into computation-intensive ones and communication-intensive ones. For computation-intensive applications, the throughput of a DSPE is limited by the computation power of the system. Therefore, realizing objective 1 is more important to this kind of applications than realizing objective 2. On the other hand, for communication-intensive applications, the throughput is limited by the network bandwidth. Thus, objective 2 is more important.

For each task deployment, if we can calculate the expectation of k and the values of ${CC}_{n\to {n}'}$ and ${PC}_{w}$, we can find the optimal deployment. Unfortunately, all these parameters are related to task deployment and the throughput and distribution of the data flow. As the data flow changes over time, we need an online task deployment strategy to adjust the current task deployment to adapt to the change of the data flow. However, it is inefficient to re-deploy all tasks at once, which was proposed in T-Storm^[6] and TS-Storm^[7], because such a scheme will cause high computing costs. On the other hand, migrating a large number of tasks at once will also increase the system’s instability. Therefore, we propose OTD, which can gradually change the current task deployment according to the properties of applications, make the task deployment adaptive to dataflow changes, and ensure the system’s stability.

4.2   Implementation of OTD

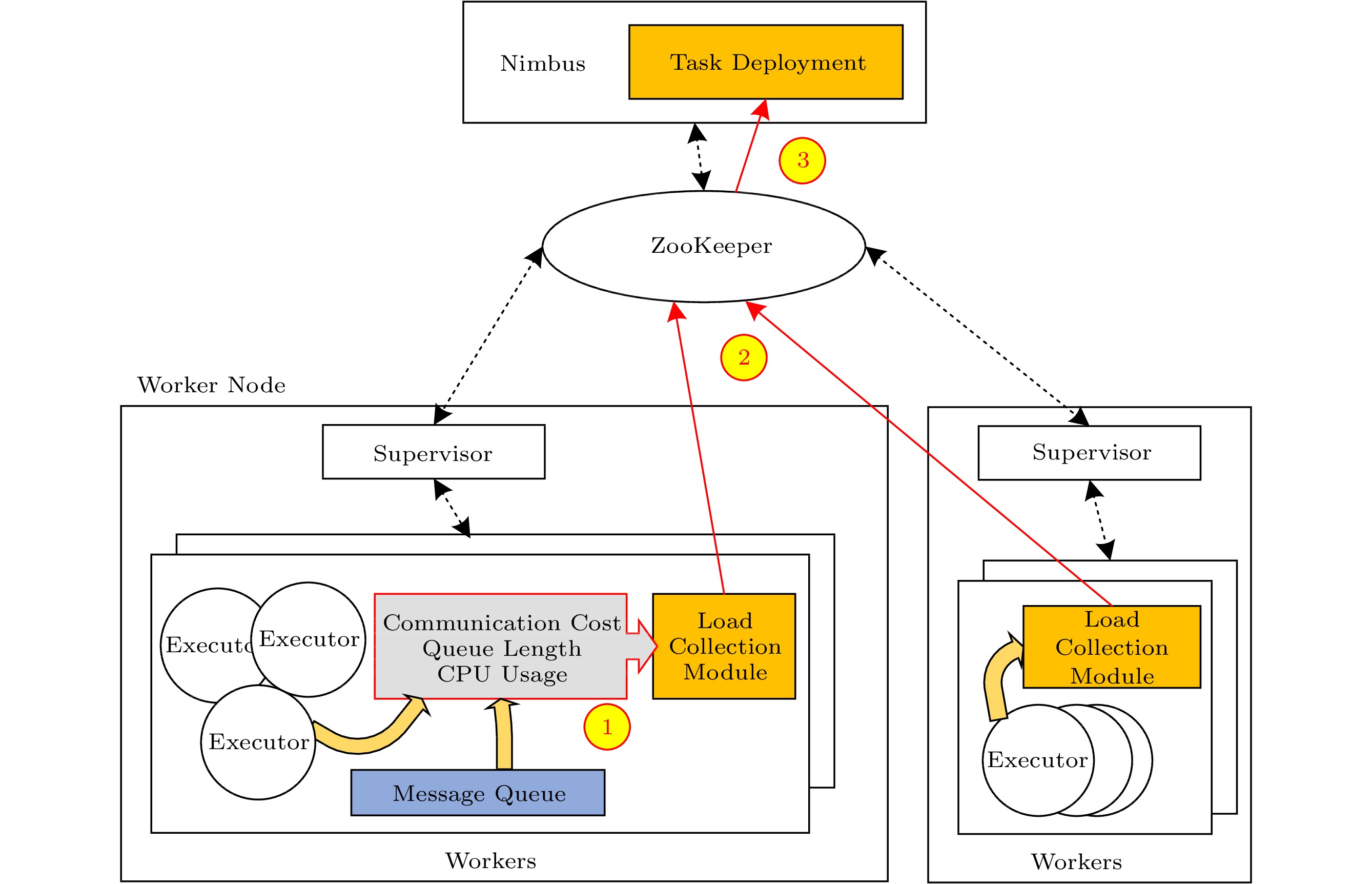
OTD is proposed to realize objective 1 and objective 2, i.e., avoiding the overload of Workers and reducing the communication costs between nodes. It consists of two modules, namely a load collection module and a module for task deployment, as shown in Fig.5. The load collection module is deployed on Workers and is responsible for collecting the communication cost between Executors, the length of each message queue, and the CPU utilization of each Worker. It will send the collected information to ZooKeeper. The module of the task deployment runs on Nimbus. It is responsible for obtaining the information collected by the load collection module from ZooKeeper and performing the online task deployment algorithm (see Subsection 4.3).

Figure  5.  Architecture and load collection flow of OTD. The black dotted arrow is the original control flow of Apache Storm, and the red solid arrow is the new statistical data flow of OTD.

下载: 全尺寸图片 幻灯片

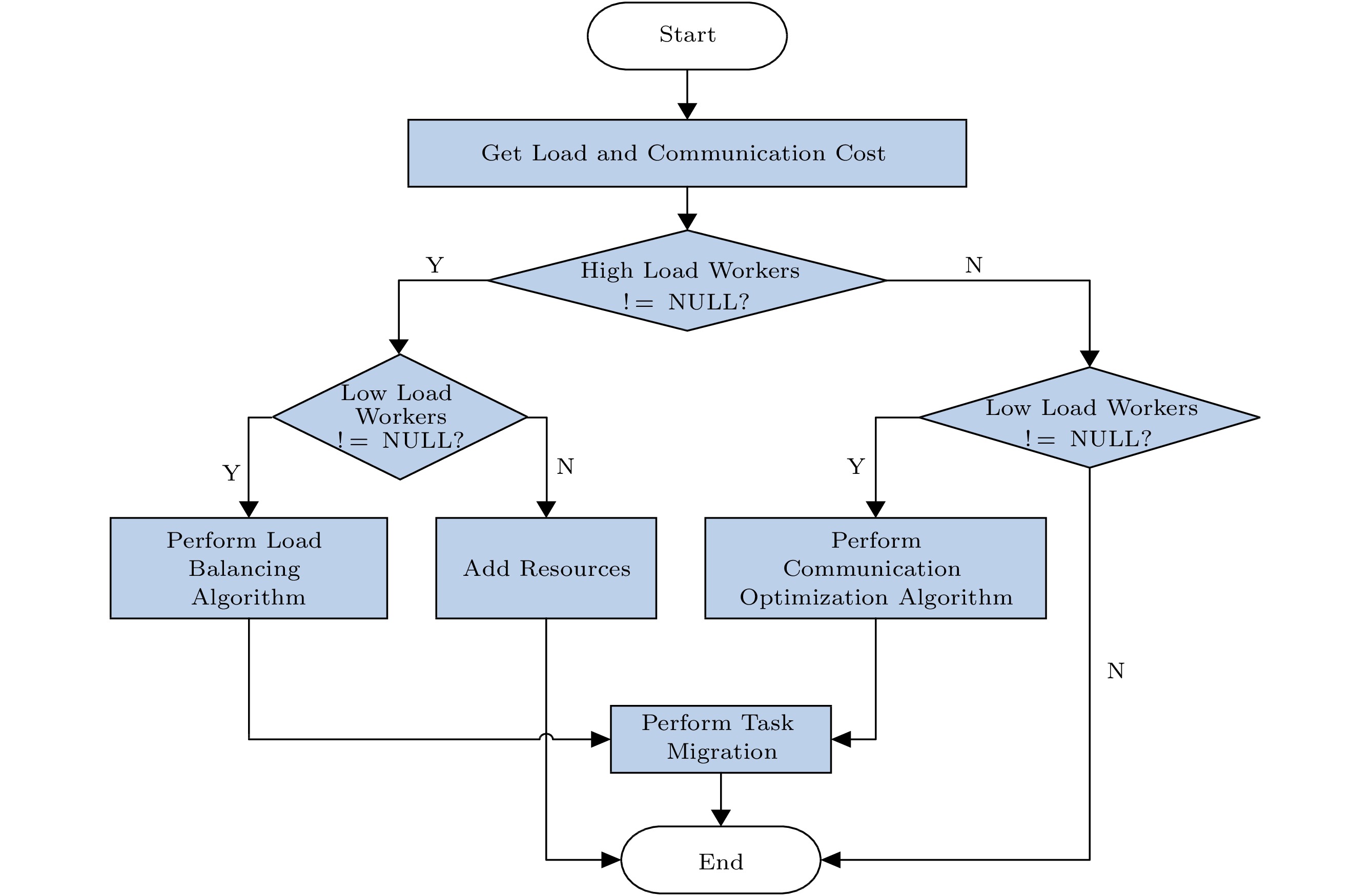
The working process of OTD is shown in Fig.6. First, we get the Worker loads and the communication costs from ZooKeeper. Then, according to the length of message queues and the CPU utilization of each Worker, we can distinguish high-load Workers and low-load Workers from normal-load Workers. Finally, according to the results of classification, we perform appropriate operations as follows.

Figure  6.  Working process of OTD.

下载: 全尺寸图片 幻灯片

Case 1. If both high-load and low-load Workers exist, we execute the load balancing algorithm (see Algorithm 1) to migrate one task from a high-load Worker to a low-load Worker.

Case 2. If high-load Workers exist, but no low-load Workers live, we send the user a warning message to inform him/her of lacking resources.

Case 3. If high-load Workers do not exist, but low-load Workers exist, we execute the communication optimization algorithm (see Algorithm 2) to reduce the inter-node communication costs.

Case 4. If neither high-load Workers nor low-load Workers exist, meaning that the system usually is running, we need not take any actions.

For case 1 and case 3, the load balancing algorithm and the communication optimization algorithm will be invoked to generate a new allocation plan, which will determine the best-fit Executor and perform a task migration that is supported by N-Storm. To minimize the impact of task migrations on the system, we only generate one best-fit pair each time, including one Executor and a targeted Worker. We periodically execute the best-fit pair selection until the current task deployment is suitable for the current data flow.

4.3   Task Deployment Algorithm

The key issue of OTD is to determine the best-fit Executor and Worker. Based on this best-fit selection, we can then invoke N-Storm to perform a task migration. For different types of applications, we optimize for application bottlenecks. In particular, for computation-intensive applications, we optimize the task deployment mainly toward objective 1. On the other hand, for communication-intensive applications, we take objective 2 as the primary objective.

To measure the quality of task deployment, we introduce the allocation score of a task as a metric. We get the allocation score by calculating the running state of the system. Let ${AS}_{e,n}$ represent the allocation score of allocating Executor e to Worker n, and we define ${AS}_{e,n}$ as the difference between the intra-node communication cost of e and the inter-node communication cost of e, as shown in (4).

Here, the variables ${CC}_{{e}'\to e}$ and ${CC}_{e\to {e}'}$ represent the intra-node communication costs sent to and from e, respectively. The variables ${CC}_{{e}'' \to e}$ and ${CC}_{e\to {e}''}$ represent the inter-node communication costs sent to and from e, respectively.

In a task deployment, we calculate the change of the allocation score to measure the benefit of current task migration. We use ${ASC}_{e,{n}_{0}\to n}$ to represent the change of the allocation score of migrating Executor e from Worker n₀ to Worker n. The calculation is shown in (5).

In (5), the first sum is the communication cost between e and the Executors on the targeted Worker n, and the second sum is the communication cost between e and the Executors on the source Worker n₀. The value of ${ASC}_{e,{n}_{0}\to n}$ is used in both the load balancing algorithm and the communication optimization algorithm.

The load balancing algorithm is shown in Algorithm 1. First, the algorithm selects the Worker with the highest load, denoted as max_load_worker, from the high_load_workers set. Then, we get all Executors who are deployed on the Worker identified by max_load_worker. These Executors are denoted as executors. Next, we select the Worker with the lowest load on each Worker node, denoted as min_load_workers, from the low_load_workers set. After that, we connect the selected Executors in executors to the Workers in min_load_workers and use (5) to calculate the change of the allocation score for each candidate migration pair. Finally, we return the migration pair which has the maximum value of ${ASC}_{e,{n}_{0}\to n}$ as a result.

The communication optimization algorithm is shown in Algorithm 2. This algorithm is similar to the load balancing algorithm, with only two differences. First, for the input, it uses all Executors in the Topology instead of the Executors in max_load_worker. Second, at the end of Algorithm 2, it determines whether the value of ${ASC}_{e,{n}_{0}\to n}$ of the migration pair to be returned exceeds a threshold (threshold_ASC). This is because a task migration will cause some fluctuation in the system performance. Thus, we need to evaluate the benefit of the selected migration. We only perform the selected task migration when the benefit exceeds the threshold. Such a scheme is introduced to avoid the task migrations that incur high costs and impact the stability of the system.

The complexity of the OTD algorithm is $O(| E |\times | N |)$, where $| E |$ is the count of Executors, and $| N |$ is the count of Workers. To ensure the stability of the system, we execute the OTD algorithm periodically. Thus, it will not introduce excessive computing load to Nimbus.

5.   Performance Evaluation

5.1   Experimental Setup

For the experiments in this paper, if there is no additional description, the default configuration described in this subsection is used.

The experiments use the distributed remote procedure call (DRPC)^[2] to provide input data to the system. DRPC consists of DRPC servers and DRPC clients and is responsible for the communication between the user and the system. Due to the budget limit, we run experiments by default on a local cluster consisting of three servers, each equipped with two Intel Xeon e5-2620 v4 CPUs and 128 GB memory. Nimbus and the DRPC server runs on one server, and the other two servers are used as Worker nodes. Thus, each Worker node has four Workers with equivalent resources. The DRPC client runs on a personal computer equipped with an Intel Core i5-4590 CPU and 8 GB memory. In addition, to verify the scalability of online task deployment, we also run an experiment on a cloud platform, which will be discussed in Subsection 5.3.

We use a linear Topology with two Bolts for the experiments. The template of the linear Topology is shown in Fig.7. For the experiments in Subsection 5.2 and the communication-intensive experiments in Subsection 5.3, we use the Word Count Topology ⁵. The input of the Word Count Topology is English sentences. Bolt 1 divides sentences into words, while Bolt 2 counts the number of word occurrences and outputs statistical results. We randomly select sentences from the novel “Harry Potter” as inputs. The Topology parallelism represents the number of Workers used by the Topology, which is set to 8. The operator parallelism means the number of tasks that run the computational logic of the operator. The parallelism of Bolt 1 and Bolt 2 is set to 12 and 24, respectively. For the computation-intensive experiments in Subsection 5.3, Bolt 1 is an operator with heavy computations, and Bolt 2 is an operator with few calculations. The parallelism settings are the same as before.

Figure  7.  Template of the linear Topology.

下载: 全尺寸图片 幻灯片

5.2   Performance of N-Storm

To test the performance of N-Storm, we implement a random task re-deployment algorithm to trigger task migrations. The algorithm can generate the required number of migrated tasks and ensure that the tasks are evenly distributed after the migration. We set the period of task re-deployment to 60 seconds. The experimental results are the total value or average value of the system running for 600 seconds.

Note that there are three important parameters in this experiment, namely M, T_S, and T_W. The parameter M represents the number of the Executors to be migrated in each task re-deployment. The parameter T_S represents the cycle that the Supervisor visits ZooKeeper to get the allocation plan, and T_W represents the cycle that each Worker visits the K/V store to get the allocation plan. To ensure the fairness of the comparison, we let supervisors execute the process-level task management (i.e., kill/start Workers) every T_W seconds in the comparative experiments. The default settings are M = 1, T_S = 10 seconds, and T_W = 3 seconds.

We compare N-Storm with several existing schemes, which are summarized below.

1) Storm. It uses the rebalance command before a task migration, which is recommended by Storm and has been used by prior work^[12-14].

2) Storm*. This scheme is the task migration algorithm proposed in T-Storm^[6] and TS-Storm^[7]. It directly dispatches the new allocation plan to supervisors, and then supervisors kill or start Workers.

3) N-Storm. This is the scheme proposed in this study. It uses the thread-level migration policy based on the task-resource decoupling design, but it does not use the optimization strategies proposed in Subsection 3.3 and Subsection 3.4.

4) N-Storm+. This scheme extends N-Storm by adding the two optimization strategies proposed in Subsection 3.3 and Subsection 3.4, respectively.

5.2.1   One-Task Migration

In the first experiment, we compare the performance of one-task migration of N-Storm with that of Storm and Storm*. We use the default settings of M, T_S, and T_W.

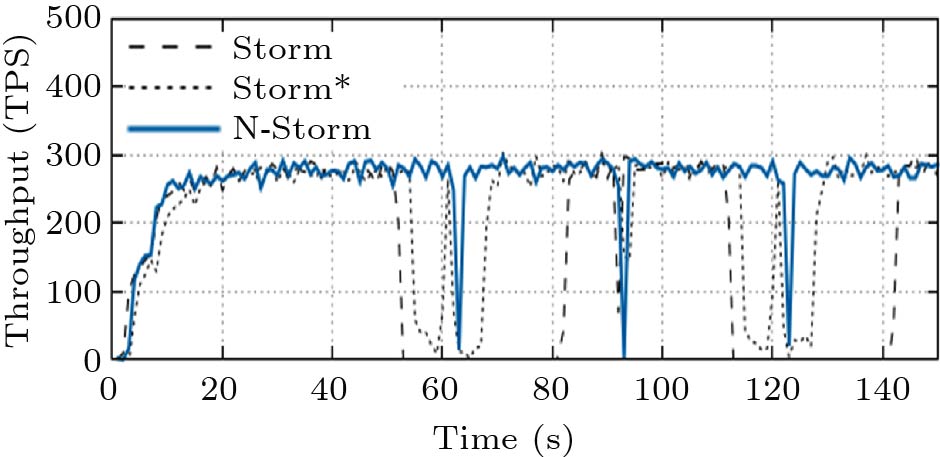
First, we record the real-time throughput of the three methods, as shown in Fig.8. The unit of the throughput is tuples per second (TPS). In the stable running stage, the throughput of the three methods is very close, indicating that N-Storm performs as well as Storm when task migrations are not invoked. We make the first task migration at the 50th second. Storm needs to suspend the running of the Topology before the task migration, and the entire stop time is around 30 seconds, which is close to the default downtime set in Storm. During this time, we can see that the system throughput drops to 0. The throughput of Storm* also decreases by more than a half, which is far below the normal throughput. The low throughput keeps about 10 seconds. This is because that the task migration in Storm* will stop Workers related to the migration.

Figure  8.  Throughput comparison for the one-task migration.

下载: 全尺寸图片 幻灯片

Meanwhile, as Storm* does not affect other Workers that are not involved in the migration, it has shorter system-stop time than Storm. N-Storm reduces the system-stop time to less than one second, which is much better than Storm and Storm*. As a result, N-Storm can perform task migration while meeting QoS requirements for real-time applications, i.e., second-level response latency.

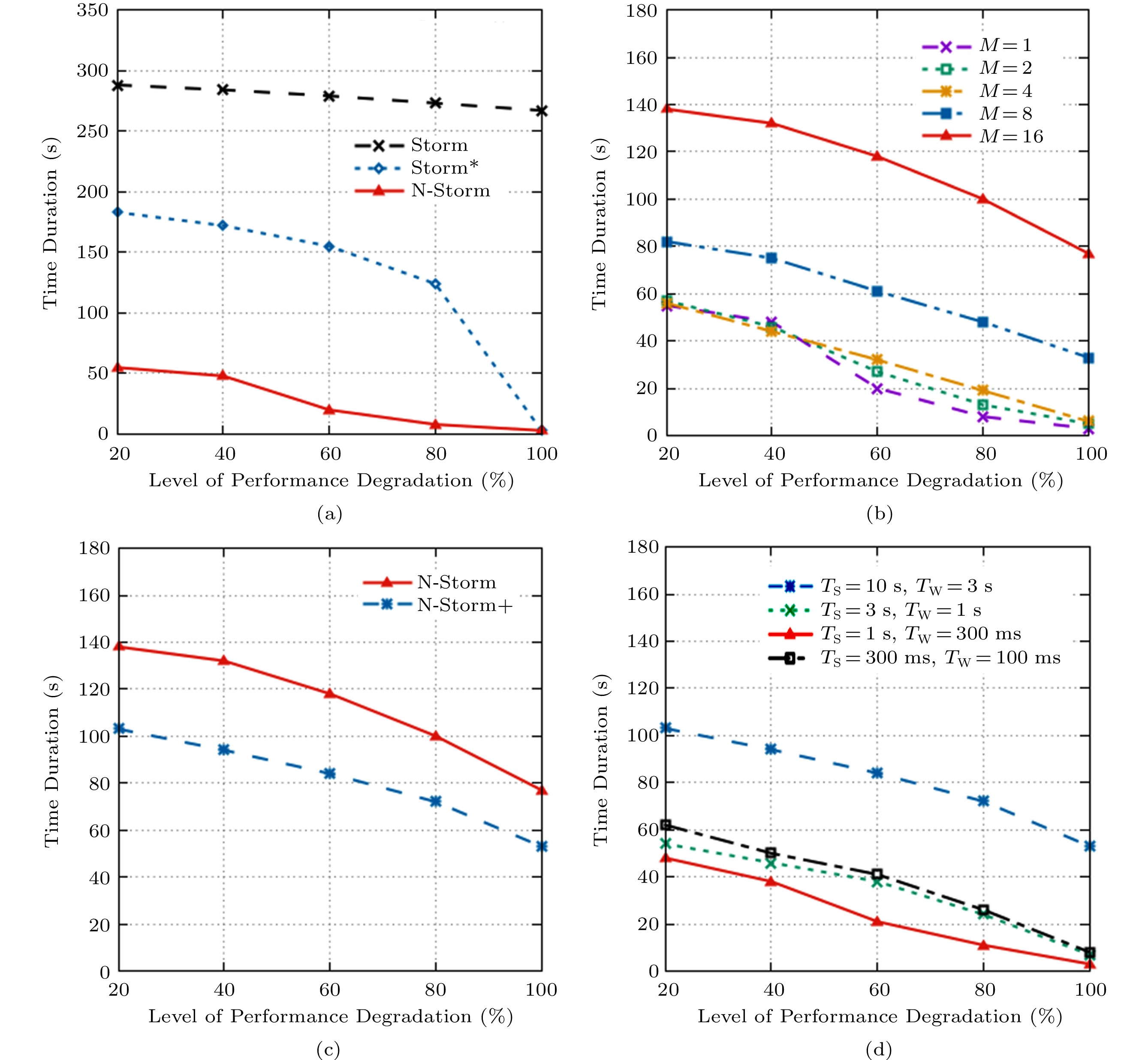
In the remaining experiments in this subsection, we measure the average throughput per second of Storm without any task migration as a baseline and count the duration of performance degradation at different levels. The level of performance degradation is set to 20%, 40%, 60%, 80%, and 100%, respectively (see Fig.9). We specially focus on the levels of 60% and 100%. If the performance degradation level is over 60%, the system performance is seriously worse. In addition, a 100% drop performance means that the system is stopped. As shown in Fig.9(a), Storm incurs a total of 279 seconds, during which the system performance decreases by 60%, and 267 seconds in case of 100% degradation. Storm* reduces the duration of 60% performance degradation to 155 seconds, 44% less than that of Storm. However, the duration still accounts for more than 25% of the total system running time.

Figure  9.  Time duration of performance degradation. (a) One-task migration. (b) Multiple-task migration. (c) Lazy task killing. (d) Impact of T_S and T_W.

下载: 全尺寸图片 幻灯片

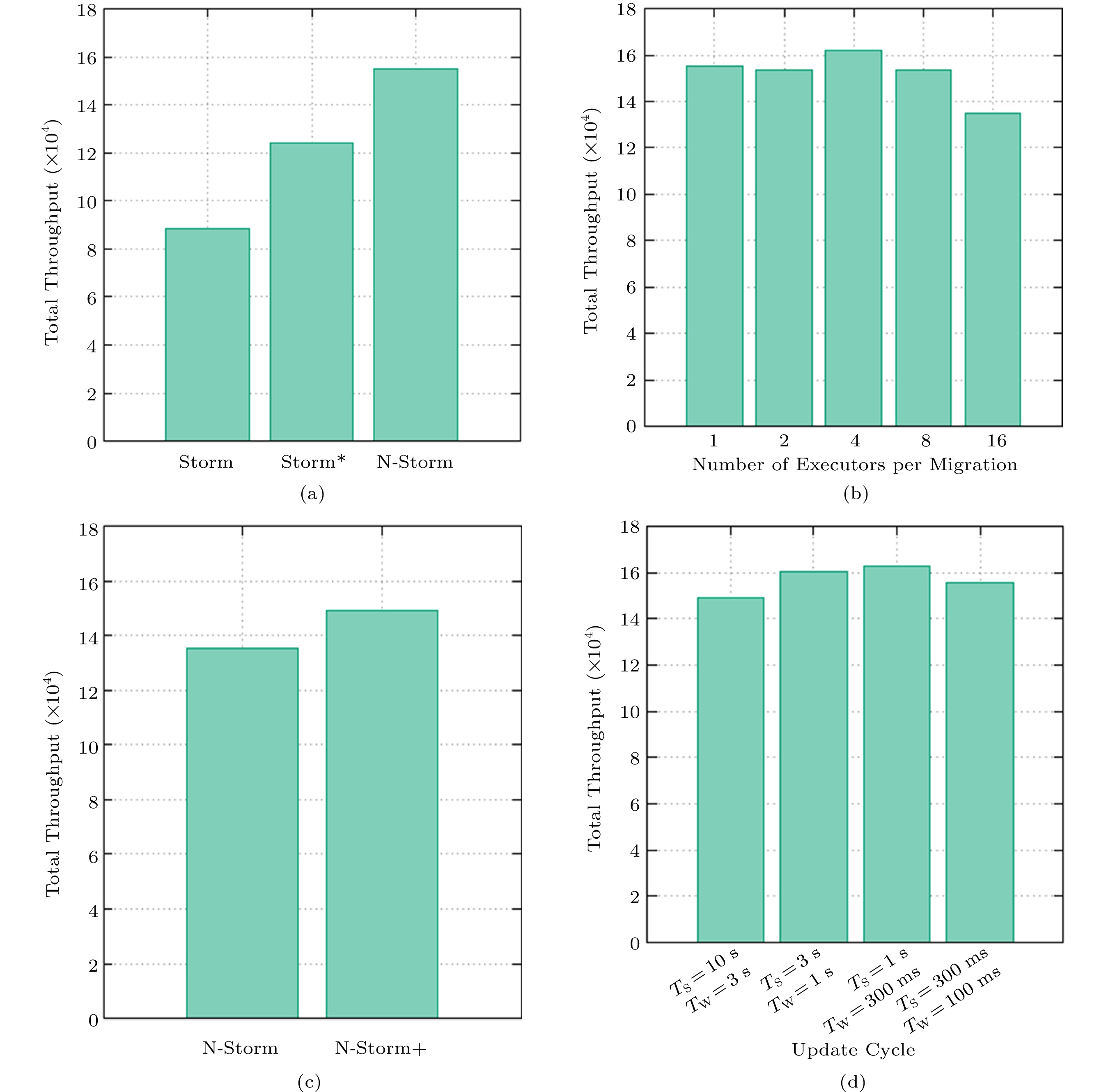
In contrast, N-Storm only costs 20 seconds at the level of 60% performance degradation, 93% less than that of Storm, and 87% less than that of Storm*. Fig.10(a) shows the total throughput of the system. We can see that Storm has the lowest throughput, and the throughput of Storm* is 41% higher than that of Storm. N-Storm has the highest throughput, which is 25% higher than that of Storm*, and 75% higher than that of Storm.

Figure  10.  Total throughput during the running of the system. (a) One-task migration. (b) Multiple-task migration. (c) Lazy task killing. (d) Impact of T_S and T_W.

下载: 全尺寸图片 幻灯片

5.2.2   Multiple-Task Migration

In this experiment, we evaluate the performance of N-Storm for multiple-task migration, i.e., each migration involves multiple tasks. We treat M as a variable and set the values of T_S and T_W with default settings.

Fig.9(b) shows the different durations of performance degradation under different values of M. When M is set to 1, 2, and 4, respectively, there are few differences in the duration of performance degradation in the five levels. However, when M is set to 8 and 16, the duration of performance degradation significantly increases, and the system throughput drops to 0 in many cases. Especially when M = 16, the duration of 60% performance degradation is 118 seconds. Fig.10(b) shows the total throughput of N-Storm under different values of M. Only when M = 16, the total throughput decreases significantly. When M is set to 1, 2, 4, and 8, respectively, the total throughput is not significantly varied. Surprisingly, the total throughput at M = 4 is greater than that at M = 2. By looking at throughput per second over the entire experiment, we find that when M = 4, after two or three task re-deployments, the throughput increases by about 5% compared with the initial state of the system. The migrated Executors are randomly selected, which means that the initial task deployment is not so efficient as the random task deployment.

5.2.3   Lazy Task Killing

In this experiment, we set T_S = 10 seconds, T_W = 3 seconds, and M = 16. Previous experiments have shown that N-Storm does not perform well in this setting. We optimize N-Storm (the optimized N-Storm is denoted as N-Storm+) by delaying the killing of Executors and setting the default delay time D_K = 2 seconds. This delay is sufficient to ensure that the system can finish the processing of the tuples in the message queue. We compare the performance of N-Storm+ and N-Storm under the same settings.

Fig.9(c) shows the duration of the performance degradation. We can see that the degradation time of N-Storm+ is less than that of N-Storm in all five levels. Among them, the duration of N-Storm+ at the 60% level is 84 seconds, which is 29% less than that of N-Storm. The duration of N-Storm+ at the 100% level is 53 seconds, which is 31% less than that of N-Storm. Fig.10(c) shows that the total throughput of N-Storm+ is 11% higher than that of N-Storm. In conclusion, the experimental results have shown that it is more efficient to delay the killing of Executors when performing task migrations in N-Storm.

5.2.4   Impact of T$_{\rm S}$ and T$_{\rm W}$

In this experiment, we study the impact of T_S and T_W on the performance of N-Storm+. All experiments are based on N-Storm+, and M is set to 16. Since a Supervisor gets messages from ZooKeeper and sends them to Workers through the K/V store, T_W should be less than T_S. We let T_S be about three times of T_W, which is similar to the default setting in Storm. Then, we reduce the values of T_S and T_W to report the duration of performance degradation.

Fig.9(d) shows the duration of performance degradation under four settings of T_S and T_W. We can see that the performance degradation time of the system continues to decline with the decreasing of T_S and T_W in the first three settings. However, in the last setting, where T_S = 300 milliseconds and T_W = 100 milliseconds, the performance degradation time of the system is longer than that of the second and the third settings. Fig.10(d) shows the total throughput under different updating cycles. Again, the results are consistent with those in Fig.9(d).

In conclusion, the experimental results confirm our analysis in Subsection 3.4. In general, a short synchronization cycle can lead to higher system performance. However, the cycle should not be set too short; otherwise, the additional communication costs will outweigh the benefit. In the followings, we analyze the communication costs of the task management at each Worker node.

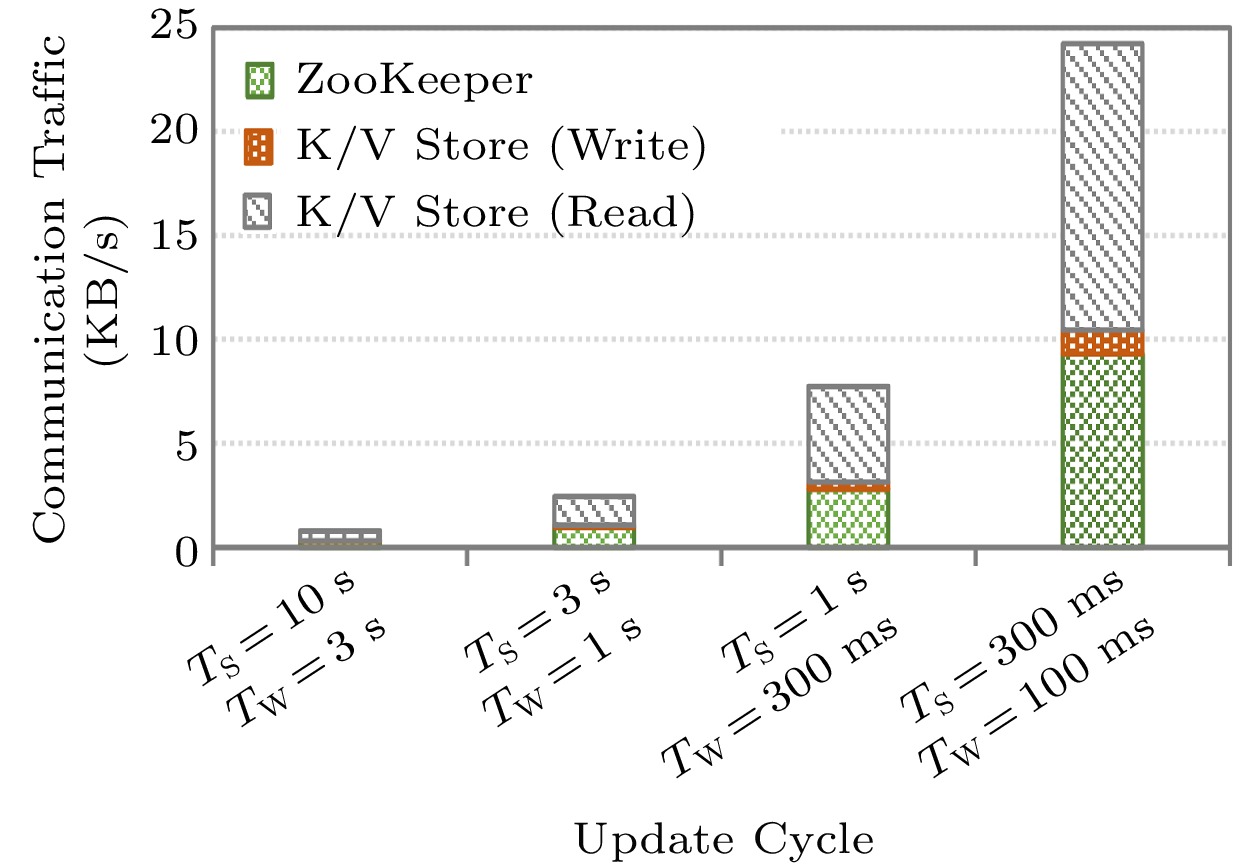
5.2.5   Communication Costs

As shown in Fig.11, we use the communication traffic per second to estimate communication costs. The results show that the communication costs increase rapidly with the shortening of the synchronization cycle. This finding supports the previous result, i.e., the moderate synchronization cycle is the best.

Figure  11.  Communication costs of the task management at each Worker node.

下载: 全尺寸图片 幻灯片

Further, we classify communication costs into three categories: communication with ZooKeeper, writing to the K/V store, and reading from the K/V store. The communication cost with ZooKeeper in N-Storm is the same as all previous methods^{[6, 7]}, and thus we only focus on the reading and writing costs caused by the K/V store. Note that the writes to the K/V store need to consume disk I/Os, while most reads to the K/V store only cost memory access. Thus, the communication costs of the K/V store are dominated by the writes to the K/V store. Fig.11 shows that N-Storm has few writes to the K/V store, indicating that N-Storm does not introduce high extra communication costs.

5.3   Performance of OTD

In this subsection, we evaluate the performance of OTD. Since all known online task deployment algorithms can cause more than 10 seconds of downtime during task migration, they cannot be invoked frequently. As a result, we only compare OTD with Storm in the experiments. Here, Storm is selected as the representative of the offline task management scheme. We aim to demonstrate that OTD can optimize the current task deployment without stopping the system for seconds. Since the role of OTD is to adjust task deployment online, its initial task deployment is the same as that of Storm.

We run OTD on computation-intensive applications and communication-intensive applications, respectively, to verify the performance. In Subsection 5.2, we observe that the CPU usage is stable at a low level for all Workers. Thus, the Word Count Topology used in the experiments can be regarded as a communication-intensive application. Therefore, in this subsection, we still use the Word Count Topology in the experiment of communication-intensive applications. We modify the code of the Word Count Topology by adding a harmonic number calculation into Bolt 1 and randomly making the distribution of the calculation in the key domain change. Consequently, we make Bolt 1 be an operator with heavy computations and Bolt 2 be an operator with few calculations.

The OTD algorithm runs on the optimized N-Storm (i.e., N-Storm+) and migrates only one task each time to minimize the performance fluctuation caused by task migrations. The cycle of task deployment adjustment is set to 5 seconds. We set T_S = 3 seconds, T_W = 1 second, and D_K = 2 seconds. We use the mean value of each performance metric (e.g., CPU usage and throughput) within 5 seconds after each task migration to show the effect of the algorithm.

5.3.1   Computation-Intensive Applications

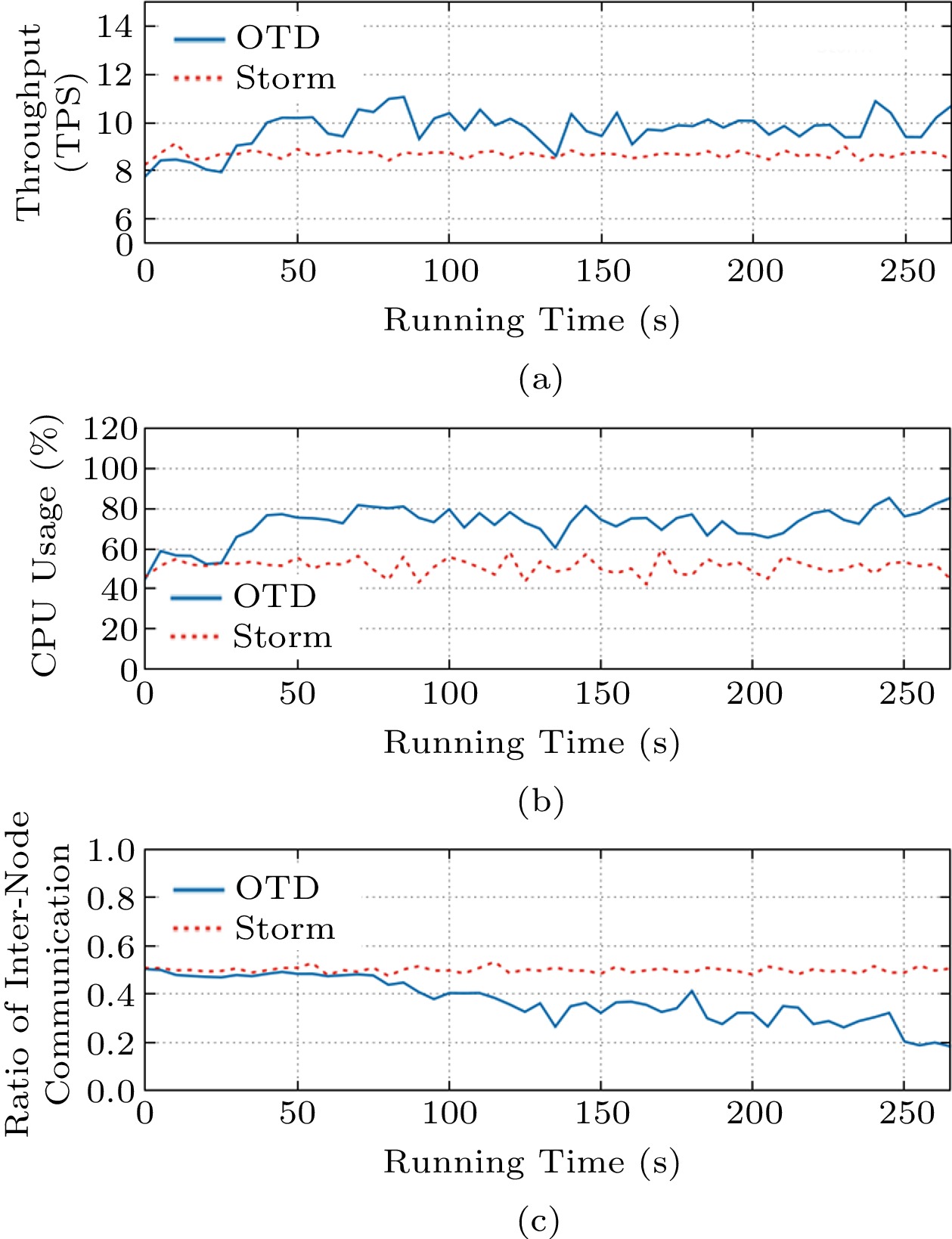
For computation-intensive applications, OTD is mainly toward the realization of load balancing, reflected by the average CPU usage of Workers. Note that Workers are the modules responsible for the processing. Our statistics of CPU usage do not include management modules such as Nimbus and Supervisors. Based on Fig.12(b), we can see that the average CPU usage of Storm is only 51%, and OTD increases the average CPU utilization to 77% after less than 50 seconds (i.e., less than 10 times of task deployment adjustment). The increase of the average CPU usage is 51%, which means that OTD makes the system load more balanced. In addition, OTD keeps the average CPU usage at 75%, although the load distribution is changing in the experiment. Fig.12(a) shows that after less than 10 times of task deployment adjustment, OTD increases the throughput by 14%, which also verifies the efficiency of the load balancing algorithm of OTD. Fig.12(c) shows that after about 250 seconds (50 times of task deployment adjustment), the ratio of inter-node communication is reduced from 50% to less than 20%. This indicates that for computation-intensive applications, OTD can effectively reduce the ratio of inter-node communication while maintaining a high level of load balancing.

Figure  12.  Performance of OTD for computation-intensive applications. (a) Throughput of the system. (b) Average CPU usage of Workers. (c) Ratio of inter-node communication.

下载: 全尺寸图片 幻灯片

5.3.2   Communication-Intensive Applications

OTD mainly aims to reduce the inter-node communication cost and the processing delay for communication-intensive applications. Fig.13(c) shows OTD can continuously reduce the ratio of inter-node communication. The reduction converges at the 305th second (i.e., after 61 times of task deployment adjustment). As a result, the ratio of the inter-node communication decreases from 50% to less than 6%. Compared with Storm, OTD reduces inter-node communication by up to 88%. Fig.13(a) shows that OTD can keep increasing the system’s throughput and maintain a high throughput after 200 seconds. After 200 seconds, the throughput of OTD increases by 19%. Fig.13(b) shows that OTD consistently reduces the processing delay of tuples. After 200 seconds, OTD reduces the processing delay by 14%. In conclusion, all the results have verified the effectiveness and efficiency of OTD.

Figure  13.  Performance of OTD for communication-intensive applications. (a) Throughput of the system. (b) Average processing delay of tuples. (c) Ratio of inter-node communication.

下载: 全尺寸图片 幻灯片

5.3.3   Scalability

In this experiment, we extend the scale of the cluster to verify the scalability of OTD. As we only have a local cluster of five servers, we run this experiment on the Huawei Cloud by buying its cloud storage and computation services. In the cloud-based experiment, all servers and clients have four vCPUs of Intel Cascade Lake 3.0 GHz and 16 GB memory. The maximum bandwidth between all servers and clients is 8 Gbit/s.

Assuming the number of Worker nodes is N_W, we use one server running the Nimbus and DRPC server and N_W servers as Worker nodes. Then, we vary N_W from 2 to 16 to evaluate the scalability of OTD. Each Worker node is configured to have two Workers. In addition, we use N_W clients to run DRPC clients. The number of tasks increases in proportion to the number of Worker nodes. Specifically, the Topology parallelism is set to $2\times {N}_{\rm W}$, the parallelism of Bolt 1 is set to $3\times {N}_{\rm W}$, and the parallelism of Bolt 2 is set to $6\times {N}_{\rm W}$. Other parameter settings are the same as in previous experiments. All results are the average value of a 600-second running.

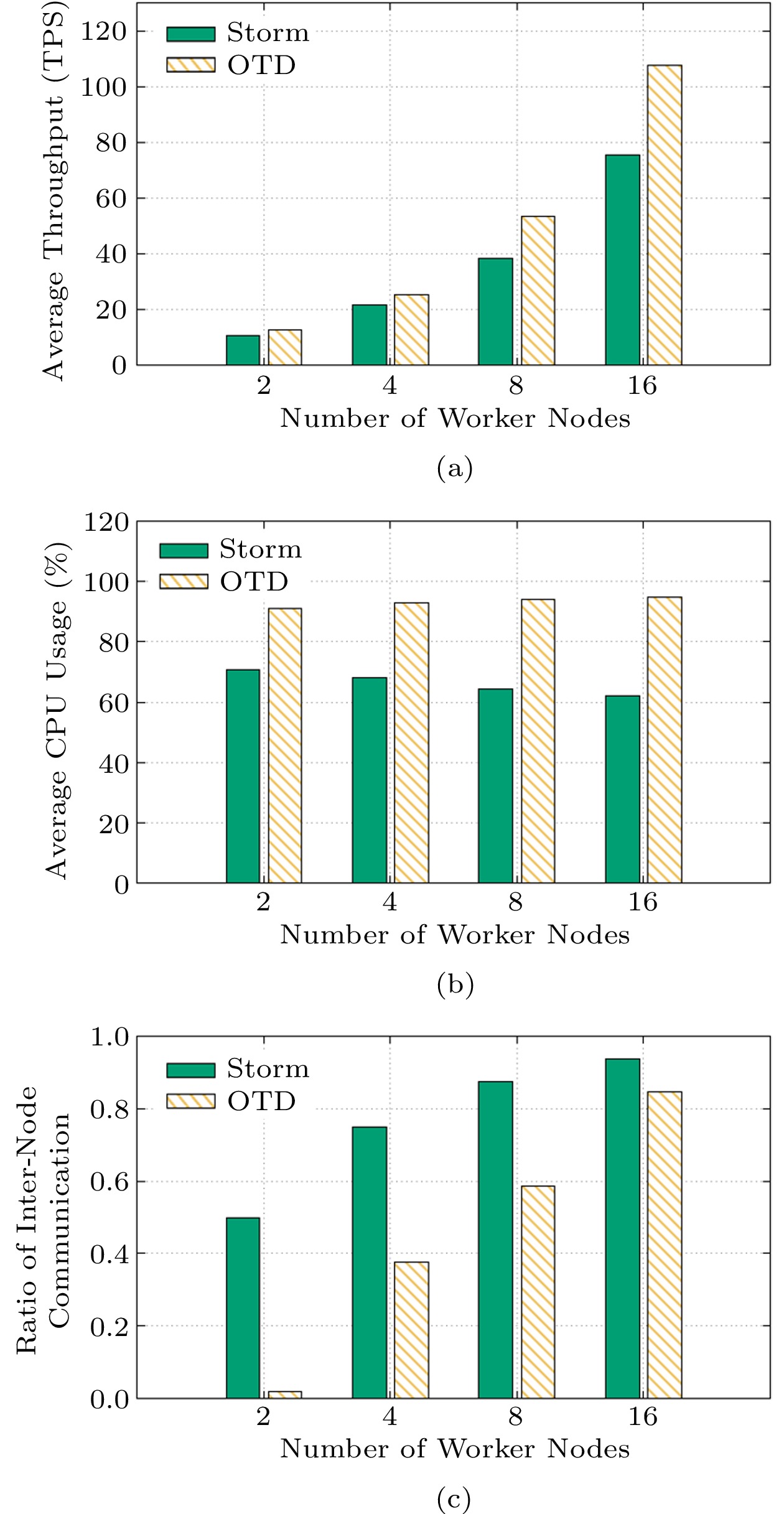
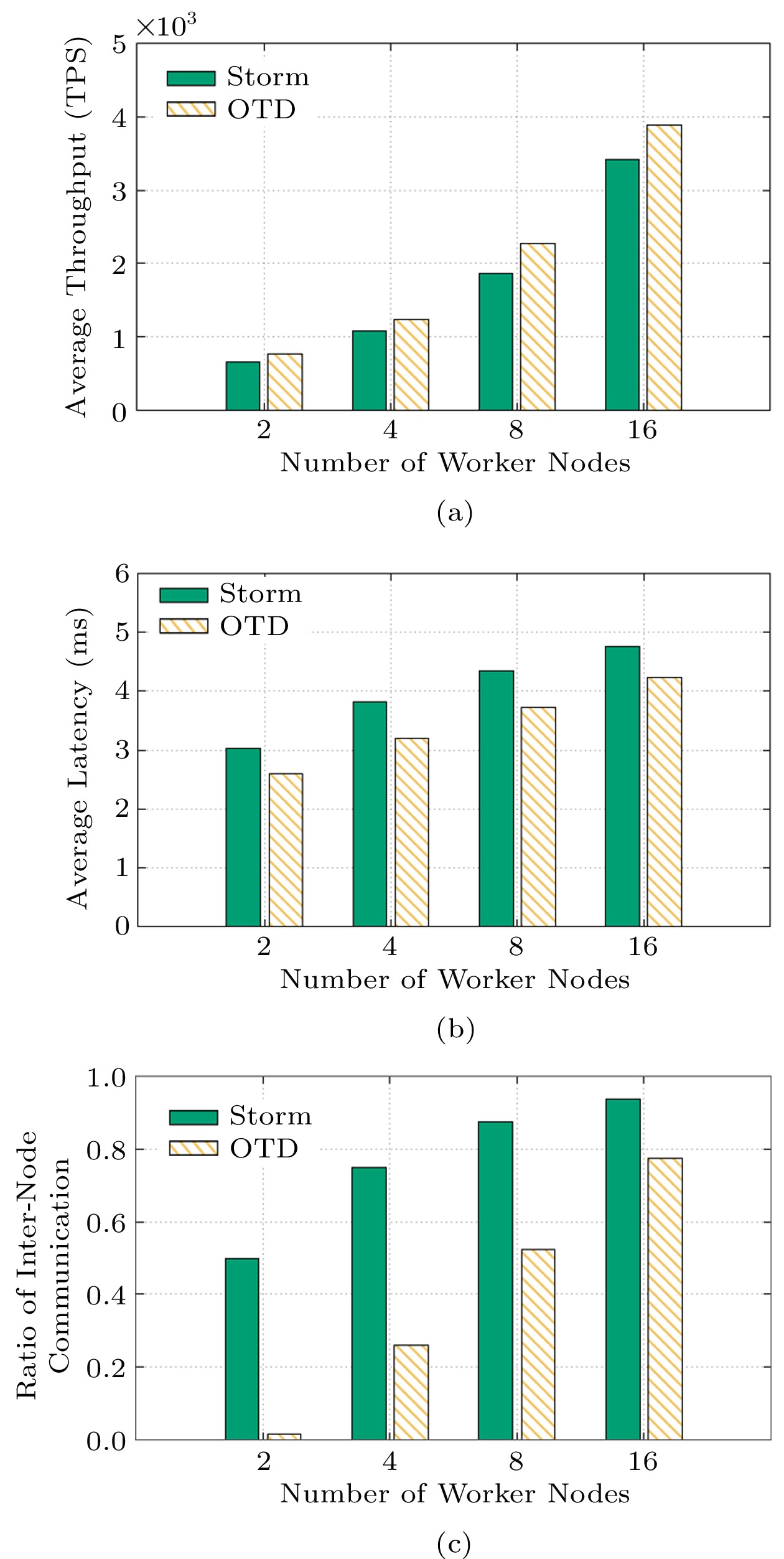
For computation-intensive applications, Fig.14(a) shows that the throughput of OTD goes up steadily with the increasing number of Worker nodes and always outperforms the throughput of Storm, indicating that OTD can maintain high performance in large-scale clusters. In addition, as shown in Fig.14(b), the average CPU usage of Storm declines slightly as the number of Worker nodes increases, while OTD keeps a stable CPU usage when the cluster size changes. As Fig.14(c) shows, OTD can keep less inter-node communication than Storm when the cluster size changes. As a result, OTD performs better on a large cluster than on a small cluster for computation-intensive applications.

Figure  14.  Scalability of OTD for computation-intensive applications. (a) Average throughput of the system. (b) Average CPU usage of Workers. (c) Ratio of inter-node communication.

下载: 全尺寸图片 幻灯片

The results for communication-intensive applications, as shown in Fig.15, are similar to those in Fig.14. We also notice that the improvement of OTD over Storm when running for communication-intensive applications is slightly worse than the results in Fig.14. That is mainly because communication-intensive applications only benefit from the OTD’s improvement in reducing inter-node communication. However, we can see that the reduction of inter-node communication in OTD generally decreases when the cluster size expands, as shown in Fig.14(c) and Fig.15(c). That is simply because of the complicated routing rules in large clusters. To sum up, it is better to use a smaller cluster for communication-intensive applications, in which OTD outperforms Storm more than running on a larger cluster. Another way is to use multiple small isolated clusters instead of a single large cluster for communication-intensive applications.

Figure  15.  Scalability of OTD for communication-intensive applications. (a) Average throughput of the system. (b) Average processing delay of tuples. (c) Ratio of inter-node communication.

下载: 全尺寸图片 幻灯片

6.   Related Work

6.1   Task Deployment and Elastic Algorithms

Offline Task Deployment. Apache Storm adopts a simple round-robin method as its default task deployment strategy. This method does not consider the cost of inter-node communication and load balancing. R-Storm^[8] maps CPU, memory, and bandwidth resources into a three-dimensional space and adopts a resource-aware task deployment algorithm. Farahabady et al.^[15] proposed a QoS-based task deployment algorithm, which allocates resources based on the QoS requirements of the data flows. Jiang et al.^[16] proposed a task deployment algorithm based on graph division. Nardelli et al.^[17] proposed a general framework of the optimal task deployment and demonstrated that it solves an NP-hard problem. Therefore, several heuristics that consider the heterogeneity of computing and network resources were proposed^{[17, 18]}. Fu et al.^[1] considered the deployment of DSPEs on edge and proposed EdgeWise to optimize resource multiplexing, which uses a congestion-aware task-deployment strategy. All of the methods mentioned above use offline task deployment algorithms. The limitation of the offline solutions makes DSPEs unable to efficiently cope with time-varying data flows and real-time pluggable multiple Topologies.

Online Task Deployment. Aniello et al.^[11] proposed an online task deployment method based on communication traffics. It monitors the tuple transfer rate between Executors in real time through a monitoring module and prioritizes the Executors with heavy communication load in the same Worker. References [6] and [19] further consider the computation power of nodes. The work in the literature^{[7, 20, 21]} considered load balancing. Specifically, researchers preferred to allocate Workers to the Worker node with the lowest load^{[7, 20]}. Fang et al.^[21] dealt with the load skewness by changing the critical partition. Li et al.^[22] proposed a dynamic algorithm for the Topology optimization based on a constraint theory, which is used to eliminate the performance bottleneck of pipeline operations. Sun et al.^[23] proposed a task deployment algorithm based on the critical path. All of these methods use online task deployment algorithms. If the data flow changes, they can recalculate and update the allocation plan, triggering task migrations. However, due to the task-resource coupling design and process-level task management in DSPEs, the task migrations lead to severe performance fluctuation. Moreover, these methods calculate a new allocation plan without considering the cost of task migration. Unlike them, our algorithm gradually fine-tunes the task deployment for the sake of system stability.

Elastic Algorithms. Aeolus^[24] and DRS^[25] dynamically adjust the degree of the parallelism of operators by monitoring the data arrival rate and data outflow rate of Executors. Similarly, the studies in the literature^[26-30] proposed to regulate the resource and configuration of DSPEs automatically. Furthermore, AdaStorm^[14] and OrientStream^[31] use machine learning methods to obtain the optimal Storm parameter configuration. Specifically, AdaStorm^[14] is trained to select the parameter configuration which uses the least resources to meet user needs. OrientStream^[31] adopts an incremental learning algorithm and an integrated learning model based on AdaStorm to make the prediction results more accurate. These methods implement elastic mechanisms on DSPEs by dynamically adjusting parallelism or other parameters as needed, which triggers task splitting or merging. They use the ``rebalance'' command or similar pause-based strategies, which does not consider the efficiency of the adjustment process.

6.2   Task Migration and Elastic Supports

Task Migration in Storm. T-Storm^[6] adopts an optimization scheme to delay the killing of Workers. However, it still leads to the killing of additional Executors and needs to stop the system for about 10 seconds. Therefore, this method is not able to effectively solve the performance fluctuation problem. Yang and Ma^[32] proposed a smoothing task migration idea for Storm. They analyzed the performance cost of the task migration and proposed to change the granularity of task migration from the Worker to the Executor. This visionary work inspired our study.

Furthermore, we present a systematic framework for thread-level task migration. In addition, we propose two optimization strategies and an online nonstop task deployment algorithm. Cardellini et al.^[12] proposed a system of automatically changing parallelism and designed an interruption-recovery-based stateful task migration method. Li et al.^[13] developed an elastic mechanism that is needed to monitor the system’s state. The authors considered stateful operators and used an additional global state manager to persist the states of the operators to achieve stateful operator migrations. Shukla and Simmhan^[33] proposed several approaches for data-flow checkpoints and migrations. They also focused on the stateful migration of large data flows and were committed to eliminating message failures and tuple recalculations. The studies^{[12, 13, 33]} are all dedicated to migrating stateful operators in Storm, which conflicts with the stateless design of Storm which we have talked about in Subsection 2.1 and Subsection 3.5. Our approach is proposed for stateless operators, which aims to reduce the duration of performance degradation incurred by task migrations.

Elastic Supports. SEEP^[34] exposes the state to the DSPE through a set of state management primitives, and on this basis, realizes dynamic scaling and failure recovery. ChronoStream^[35] uses a transaction migration protocol based on state reconfiguration to support stateful task migration. Similarly, DSPEs proposed in the literature^[36-38] aim to achieve scalability. Additionally, Chi^[9] embeds the control platform into the data platform so that each task can obtain the control information and perform migrations reactively. Elasticutor^[39] allows to change the number of resources consumed by a task dynamically to achieve elasticity. Megaphone^[40] realizes dynamic task migration by changing the Topology. Rhino^[41] provides a handover protocol and a state migration protocol for a vast distributed state. These studies focus on maintaining state consistency and introduce additional costs, such as processing in full compliance with timestamp order and adding global or local routing tables. Furthermore, these migration strategies are complex and not suitable for frequent use. Differing from these researches, our research focuses on reducing the cost of task migration to achieve the stability of the system and the QoS requirements of applications.

7.   Conclusions

This paper proposed an online nonstop task management mechanism for DSPEs (distributed stream processing engines) to adapt to the time-varying data flows. The main contributions of this study include a task-resource decoupling DSPE named N-Storm that supports thread-level online task migrations and a new online task deployment method called OTD. Our experimental results showed that N-Storm can significantly reduce the time duration of performance degradation and eliminate the stop time during task migrations. Also, the OTD method can efficiently increase the average CPU usage for computation-intensive applications and reduce the inter-node communication costs for communication-intensive applications.

In the current implementation of OTD, we generated the best-fit resource allocation plan under the premise of given resources and task Topology, meaning that we only deal with the dynamical load balance among Workers by migrating the tasks in high-load Workers to low-load Workers. An interesting future research direction is to make OTD adaptive to the resource-quota change of Workers. For example, some previous studies^[24-31] proposed automatically regulating resources and dynamically adjusting the degree of operators' parallelism. In the future, we will consider this issue and offer some efficient resource rebalancing algorithms.