1.   Introduction

The growing popularity of blockchains marks the emergence of a new era of distributed computing. Blockchain, the underlying technology of Bitcoin ¹, is essentially a decentralized, immutable, verifiable and traceable distributed ledger managed by multiple participants. Specifically, blockchain can achieve trusted data sharing among untrusted parties without the coordination of any central authority.

A blockchain system commonly contains two kinds of nodes, full nodes and light clients. Full nodes receive and validate every block, and store the history of all transactions. Due to limited storage capacity, light clients only download block headers to verify the existence of each transaction by checking the root of the Merkle tree in the block header, which consumes less resources than full nodes. Any query from light clients will be forwarded to full nodes for processing. The integrity of query results returned from full nodes will be authenticated by light clients, because the full nodes may be dishonest.

However, existing blockchain systems have limited ability to support authenticated queries for light clients. For example, the simple payment verification (SPV) in Bitcoin can only answer whether a particular transaction is present in a block or not. With the popularization of the blockchain technology, there is an increasing demand for a variety of authenticated queries on the blockchain. For example, by utilizing range queries, users may want to select Bitcoin transactions satisfying “10 bitcoin $\leqslant TotalOutput$ $\leqslant$ 30 bitcoin”. Join queries combining blockchain data with off-chain data are important as well. For instance, it is easy to understand that today's Bitcoin fee is $1.5 rather than 0.00003 bitcoin, which needs to join Bitcoin data with USD-based market data. Aggregate queries are widely adopted for business applications, and thus viewing blockchain data in aggregation is useful to make business decisions. For instance, users may be interested in some aggregate information, such as “daily transaction volume”, “transactions per second” and “average transaction fee per month”. Hence, authenticated query processing becomes urgent nowadays.

In this paper, we focus on range, join and aggregate query authentications for the blockchain. How to process authenticated queries can be tracked back to outsourced databases, where clients delegate the DBMS management to a third-party database server that receives and processes queries. In a typical outsourced database, both the signature-based approach (e.g., signature chaining^[1]) and the tree-based approach (e.g., MB-tree^[2]) are capable of ensuring the correctness and completeness of query results. Since the signature-based approach cannot scale up to large datasets when each pair of adjacent tuples must be signed, we adopt the tree-based approach in this paper. However, applying existing tree-based approaches to the blockchain is quite challenging.

● In addition to the query results, full nodes need to return the verification object (VO). The construction and transmission of VO incur query latency and bandwidth consumption respectively, and the splicing and the verification of VO increase the computing overhead of light clients with limited resources.

● When a leaf node is updated, its hash change will be propagated up to the root digest, which induces write amplification. In general, the tree-based approach assumes the database needs few updates, so that it is inapplicable to the blockchain that continuously submits transactions by block.

To address the above issues, it is necessary to devise a new scheme to verify query results efficiently.

In recent years, the trusted execution environment (TEE) has caught the attention of industrial and academic communities as it provides cryptographic constructs based on hardware and offers stronger protection in comparison with its software counterparts. TEE offers a promising direction of designing query authentication schemes. For example, Intel SGX (software guard extensions)^[3], a typical TEE, can protect sensitive code and data from being leaked and tampered with, and isolate security-critical applications even from privileged users. Intel SGX allows to create one or more isolated contexts, named enclaves, which contain segments of trusted memory. To guarantee confidentiality and integrity, sensitive applications are installed in the enclave, no matter whether the underlying machine is trusted or not.

However, the security offered by Intel SGX does not come for free. The special region of isolated memory reserved for the enclave, called EPC (enclave page cache), currently has a maximal size of 128 MB, of which only 93 MB are utilizable for applications. An EPC page fault occurs when the accessed memory exceeds the available EPC size. Page swapping is expensive, because the enclave memory is integrity-protected and encrypted. Intel SGX provides two built-in wrapper codes, $ecall$ and $ocall$, to invoke enter and exit instructions respectively to make cross-enclave function calls. However, these two codes add overhead of approximately 8000 CPU cycles, compared with 150 cycles of a regular OS system call^[4]. Although Intel SGX solves the secure remote computing problem of sensitive data on untrusted servers, how to lower the expensive cost remains as an open challenge.

In summary, we first propose authenticated range and join queries for the blockchain by combining MB-tree^[2] with Intel SGX, which is an enhancement of [5]. Then, we extend the work of [5] by presenting authenticated aggregate queries that integrate AAB-tree^[6] and Intel SGX. In addition, we explore more details, e.g., the cost analysis against traditional approaches and thorough empirical evaluation. To the best of our knowledge, it is the first step toward investigating the issue of query authentication with Intel SGX over the blockchain. Our main contributions are as follows.

● We propose an efficient Intel SGX based query authentication scheme for the blockchain, with which light clients do not need to receive or verify any VO. The scheme also alleviates the cascading hash computing cost induced by updates on the MB-tree, with a hybrid index leveraging the feature of the blockchain to submit transactions by block.

● In view of the space limitation of enclave memory, we integrate the MB-tree and the AAB-tree with Intel SGX to support range and aggregate query authentications respectively.

● We conduct theoretical analysis and an empirical study to evaluate our proposed scheme. Analysis and experimental results show the efficacy of the proposed scheme.

The rest of the paper is organized as follows. Section 2 gives some preliminaries, followed by the review of existing work in Section 3. Section 4 introduces the problem formulation. Section 5 presents our scheme of query authentication with Intel SGX. The batch update is discussed in Section 6. The cost analysis and the security analysis are presented in Section 7 and Section 8 respectively. The experimental results are reported in Section 9. Section 10 concludes this paper.

2.   Preliminaries

In this section, we introduce the authenticated data structure (ADS) and Intel SGX^[3], with which we achieve efficient verifiable queries.

2.1   Authenticated Data Structure

As more users outsource their database systems to cloud service providers, query authentication has been extensively studied to ensure the integrity of query results returned by untrusted providers. In the existing solutions, ADS is more efficient and widely applied in practice. Merkle hash tree (MHT)^[7], Merkle B-tree (MB-tree)^[2] and authenticated aggregation B-tree (AAB-tree)^[6] are all typical ADSs.

MHT is a binary tree in which each leaf node corresponds to the digest of a tuple. The digest of an internal node is computed by hashing the concatenation of the digests of its two child nodes. For example, an internal node $n$ is assigned the digest value $h_n = H(h_{n_{1}} | h_{n_{2}})$, where $n_1$ and $n_2$ are the children of $n$ and $H()$ is a one-way, collision-resistant hash function. The internal nodes are iteratively constructed in a bottom-up manner. Depending on the root node that is signed by the data owner, any tampered tuple can be detected, which assures data integrity. MHT has been extensively adapted to many blockchain systems. In Bitcoin, each leaf node of MHT corresponds to the SHA256 digest of a transaction. According to the direct siblings in the path from the leaf node to the root node, light clients can use SPV to verify whether a transaction exists in a block.

MB-tree supports authenticated range queries. Each node contains $f-1$ index keys and $f$ pointers to child nodes, where $f$ is the fanout parameter. Additionally, each pointer is augmented with a digest. The exact structure of a leaf and an internal node is shown in Fig.1(a). In the leaf node, each digest is a hash value $h = H(t)$, where $t$ is a tuple pointed by the corresponding pointer. In the internal node, each digest is a hash value $h = H(h_1|...|h_f)$, where $h_1, ..., h_f$ are the hash values of the children of the internal node. MB-tree is constructed in a bottom-up manner. The contents of all nodes in the tree are reflected to the root digest that is signed by the data owner. Therefore, the entire tree can be verified by the root digest so that adversaries cannot tamper with the tree.

Figure  1.  Merkle tree. (a) Example of MB-tree nodes. (b) Example of AAB-tree nodes. The top node is an internal node, and the bottom node is a leaf node. $k$ is the key, $p$ is a pointer to the child node, $a$ is the aggregate of all children, and $h$ is the hash value associated with the entry.

下载: 全尺寸图片 幻灯片

AAB-tree, an aggregate MB-tree that combines the MB-tree with pre-aggregated results, supports authenticated aggregate queries. Besides an index key $k$ and a pointer $p$, each entry of a node is associated with an aggregate value $a$ and a digest $h$. The structures of leaf and internal nodes are shown in Fig.1(b). In the leaf node, each aggregate value is the aggregate attribute of a tuple, and each digest $h = H(k|a)$ is computed by a hash function $H()$ based on the key $k$ and the aggregate value $a$ in the same entry. In the internal node, each aggregate value is the aggregation of the children of the internal node, and each digest is a hash value $h = H(h_1|a_1|...|h_f|a_f)$ computed on the concatenation of both hash values and aggregate values of the children of the internal node. All aggregate values in an AAB-tree node at level $l$ are aggregated up to an entry in the parent node at level $l+1$, which corresponds to the roll-up materialization in the OLAP terminology. Therefore, when processing aggregate queries, we can get pre-aggregated results directly from the nodes at the upper levels of the AAB-tree without retrieving and aggregating the nodes at lower levels of the AAB-tree.

2.2   Intel SGX

Intel SGX^[3] provides an isolated portion of memory, called enclave, to protect sensitive code and data from view or modification. Applications can create an enclave to protect the integrity and the confidentiality of the code and data. Enclave memory pages, stored in the enclave page cache (EPC), are integrity-protected and encrypted. EPC is limited to 128 MB. When this limit is exceeded, enclave pages are subject to page-swapping that leads to performance degradation. Intel SGX's remote attestation allows applications to verify that an enclave runs on a genuine Intel processor with SGX. After successful remote attestation, secret data is transferred to the enclave through a secure channel. The interaction between applications and enclaves needs $ecall$ to call into enclaves (e.g., accessing enclave memory) and $ocall$ to call out of enclaves (e.g., calling OS API). The context switches induced by $ecall$ and $ocall$ drastically reduce the performance. Although Intel SGX offers a trusted computing solution based on hardware, an effective optimization strategy is needed when designing encalve-based solutions.

3.   Related Work

Query Authentication over Outsourced Databases. Existing query authentication approaches which guarantee query integrity against untrusted service providers are categorized into two kinds, signature chaining^[1] and Merkle tree^[7]. Signature chaining signs each pair of adjacent tuples in a chain fashion. Based on the aggregated signature, the server can return the VO including only one signature regardless of the result set size, and the client can verify query results with this signature. Although the signature chaining features small VO size and low communication cost, it cannot scale up to large datasets because of the expensive cost on signing adjacent tuples. Typical Merkle trees include MHT^[7] and MB-tree^[2]. MHT aims at authenticated point queries, while MB-tree combines MHT with $B^{+}$-tree to support authenticated range queries. Since MB-tree enables efficient search as $B^{+}$-tree and query authentication as MHT, it is employed to support authenticated aggregate^[6] and join^[8] queries. [6] proposes AAB-tree, a variant of MB-tree, for aggregate queries. Each entry in an AAB-tree node is associated with an aggregate value summarizing its children and a hash value computed on the concatenation of both hash values and aggregate values of its children. [8] studies the authentication of the join queries by constructing two MB-trees on two relation tables. To support authenticated multi-dimensional range queries, MMB$^{\text{cloud}}$-tree^[9] integrates a multi-dimensional indexing method (i.e., iDistance) with MB-tree. However, these studies mainly focus on outsourced databases, insufficient for blockchain systems due to poor update performance.

Query Authentication over Blockchains. SPV, introduced by Satoshi Nakamoto ², can only verify if a transaction exists in the blockchain or not. Hu et al.^[10] leveraged smart contracts for verifiable query processing over the blockchain, focusing on the file-level keyword search without investigating the indexing issue. To support verifiable boolean range queries, vChain^[11] implements an accumulator-based ADS scheme that enables aggregate intra-block data over arbitrary query attribute. vChain also builds an inter-block index that uses an accumulator-based skip list to further improve query performance. Though vChain can aggregate intra-block and inter-block records for verifiable query processing, its light clients still need to receive and verify VOs. To support authenticated range queries, Zhang et al.^[12] stored data records in traditional databases (off-chain) and MB-tree in Ethereum (on-chain). Because MB-tree is maintained by a smart contract, the main purpose of optimization is to reduce the Ethereum gas cost. Additionally, [12] focuses on verifiable queries upon traditional data, not blockchain data. SEBDB^[13] constructs an MB-tree for every block and implements block-based authenticated query processing for light clients. Since full nodes are untrusted, light clients of SEBDB reduce the risk by sampling from multiple full nodes, which further increases the verification burden of light clients. In a nutshell, how to achieve authenticated query processing at low cost is the focus of the blockchain.

Blockchain with Intel SGX. Present blockchain systems mainly perform software-based cryptographic algorithms to ensure the trust of data. The appearance of trusted hardware, Intel SGX, opens up new possibility to ensure the confidentiality and the integrity of the blockchain. Town Crier^[14], an authenticated data feed system between existing web sites and smart contracts, employs Intel SGX to furnish data to Ethereum. To serve authenticated data to smart contracts without a trusted third party, Town Crier combines the smart contract front end and the SGX back end. Ekiden^[15] performs smart contracts over private data off-chain in Intel SGX, and attests to the correct execution on-chain, which avoids consensus nodes from executing contracts and achieves the concurrent execution of contracts. With separating the consensus from the execution, Ekiden enables efficient confidentiality-preserving smart contracts and high scalability. Yan et al.^[16] presented a confidential smart contract execution engine to support on-chain confidentiality by leveraging Intel SGX. Public transactions and confidential transactions are handled in public-engine and confidential-engine respectively, while plain-text and cipher-text states are generated and stored on the blockchain. Relying on Intel SGX, Dang et al.^[17] optimized the Byzantine consensus protocol and improved the individual shard's throughput significantly. SPV in Bitcoin may leak the client's addresses and transactions. BITE^[18] prevents leakage from access patterns and serves privacy-preserving requests from light clients of Bitcoin by leveraging Intel SGX on full nodes. Although existing studies harmonize blockchain and Intel SGX, none of them explore query authentication with Intel SGX.

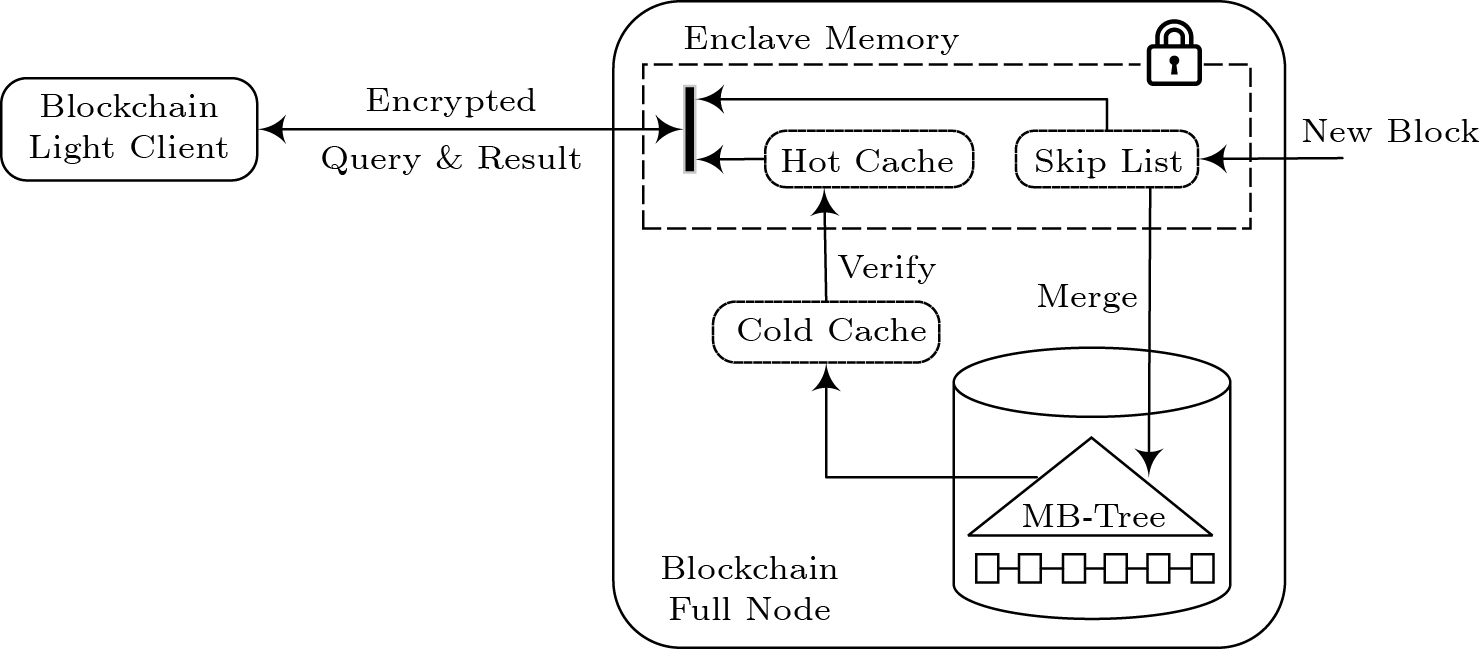
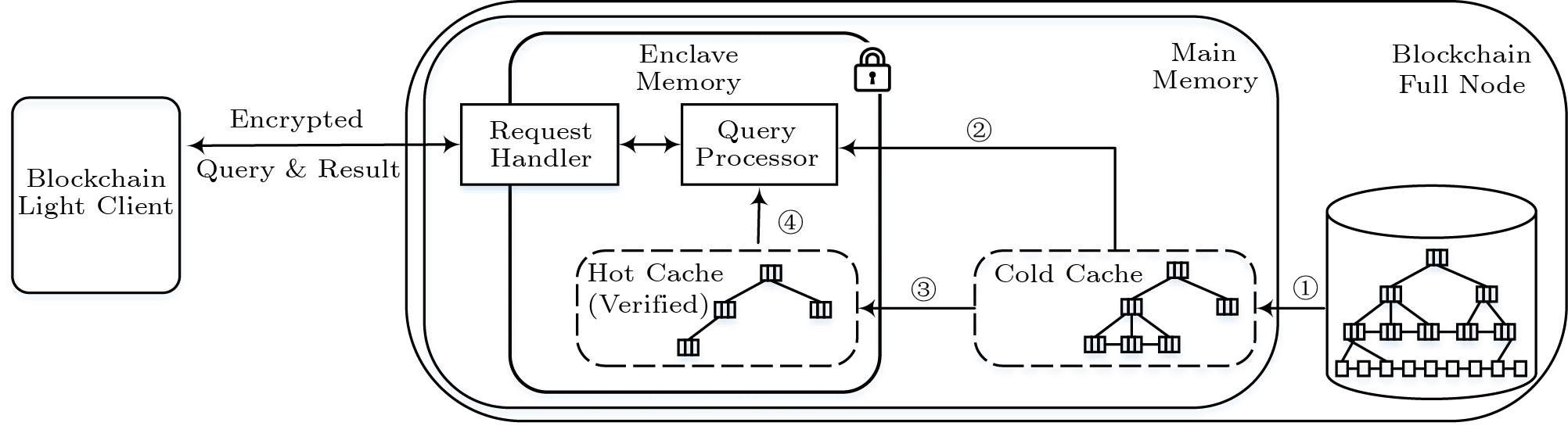
4.   System Overview

Architecture. Fig.2 elucidates our system that consists of a full node and a light client. Each query from the light client is forwarded to the full node for processing. As the full node may be dishonest, it is critical to show the integrity of query results for the light client. Traditional solutions organize data with an MB-tree, and provide the light client both query results and VOs for further verification. In our case, however, a big VO, especially when processing range queries, may exceed the processing power of the light client like a mobile device. Consequently, our system, which is equipped with Intel SGX, provides trusted query processing on the untrusted full node, and returns query results to the light client through a secure channel, which enables the light client to trust query results without receiving or verifying any VO. Due to the space limitation of enclave memory, we organize the data hierarchically in trusted memory (enclave) and untrusted memory (regular memory).

Figure  2.  Architecture of query authentication with Intel SGX.

下载: 全尺寸图片 幻灯片

In our scheme, an MB-tree is constructed for the entire blockchain data, given that one MB-tree per block imposes more complexity for query processing. The skip list in the enclave memory buffers newly appended blocks, and merges the block data into the MB-tree periodically once the used memory exceeds the predefined threshold. Our scheme maintains two kinds of caches, including a hot cache in the enclave memory and a cold cache in the regular memory. The hot cache caches frequently-accessed MB-tree nodes that will not need to be verified in future. The cold cache caches MB-tree nodes to reduce disk I/O. More details are discussed in Section 5 and Section 6.

Adversary Model. Since no participant in the blockchain network trusts others, the full node is a potential adversary and may return incorrect or incomplete query results. In our scheme, we apply Intel SGX to process queries with integrity assurance. Because the enclave memory space is limited, we employ an authenticated index structure, MB-tree, outside the enclave memory to guarantee data integrity. Even though an adversary may compromise the operating system and other privileged software on a full node, it cannot break the hardware security enforcement of Intel SGX. With our hardware-based scheme, the light client can trust the correctness and the completeness of query results under the following criteria.

● Correctness. All results satisfy the query conditions and have not been tampered with.

● Completeness. No valid result is omitted regarding the query range.

5.   Query Authentication with Intel SGX

As Intel SGX can protect the code and data from being leaked and tampered with, an ideal solution is to install the entire storage engine and process all queries in the enclave, which eliminates computing and network overheads induced by the VO in traditional solutions. However, the limited enclave size makes it infeasible to handle large datasets. In this study, we design a scheme to organize data hierarchically in trusted and untrusted memory. Meanwhile, the data in the untrusted memory is organized as an MB-tree and the frequently-accessed internal nodes are cached in the enclave as trusted checkpoints. A skip list, maintained in the trusted memory, buffers newly appended block data. Once the size of the skip list reaches a threshold, we merge all data in the skip list into the MB-tree.

5.1   MB-Tree in Intel SGX

In our scheme, the root node of the MB-tree^[2] is always located in the enclave, while the rest nodes will be loaded into the enclave according to query requests. After verifying the Merkle proof, a node is trusted for search. The frequently-accessed nodes are cached in the enclave to implement verifiable queries cheaply, and the other nodes are outside of the enclave to save enclave usage. The MB-tree can be constructed either from scratch or based on existing data. The enclave on the full node is firstly authenticated with Intel SGX's remote attestation. Then the root node of the MB-tree is transferred into the enclave through a secure channel. When the thread maintaining the MB-tree in the enclave receives a new block, it begins to extract and verify transactions in the block based on verification rules of the blockchain.

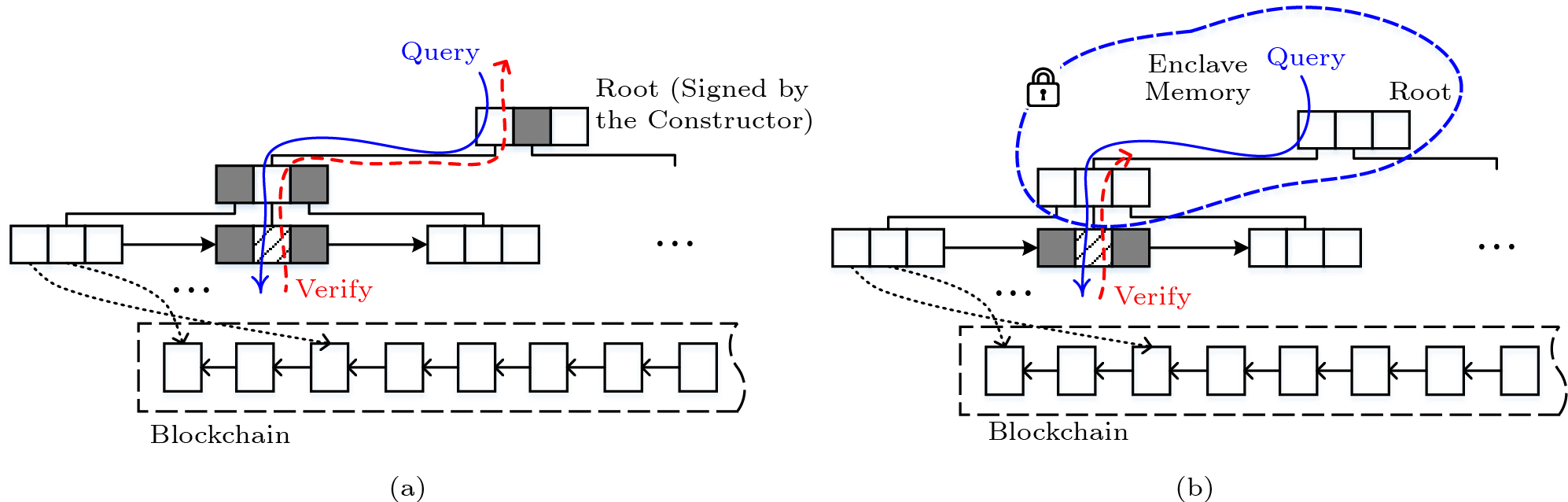
As shown in Fig.3(a), the traditional point query on the MB-tree returns the VO (gray boxes in Fig.3) in addition to the query result (oblique line boxes in Fig.3). The VO is composed of sibling hashes in each node along the query path. Light clients recompute the root digest based on the query result and VO, so as to verify the correctness of the query result. For authenticated point queries, the size of the VO is much greater than that of the query result, which incurs significant communication cost.

Figure  3.  Point query and verification on MB-tree. (a) Point query. (b) Point query with Intel SGX.

下载: 全尺寸图片 幻灯片

For the point query with Intel SGX, because the previously verified MB-tree nodes in the enclave are trusted, only the nodes outside the enclave need to be verified, as described in Fig.3(b). When recomputing the root digest in a bottom-up manner along the verification path, the verification process may be stopped early once finding a node located in the enclave, which shortens the verification path (dash arrows in Fig.3(b)). In addition, since the SGX has verified VOs instead of light clients, light clients just need to receive the query result.

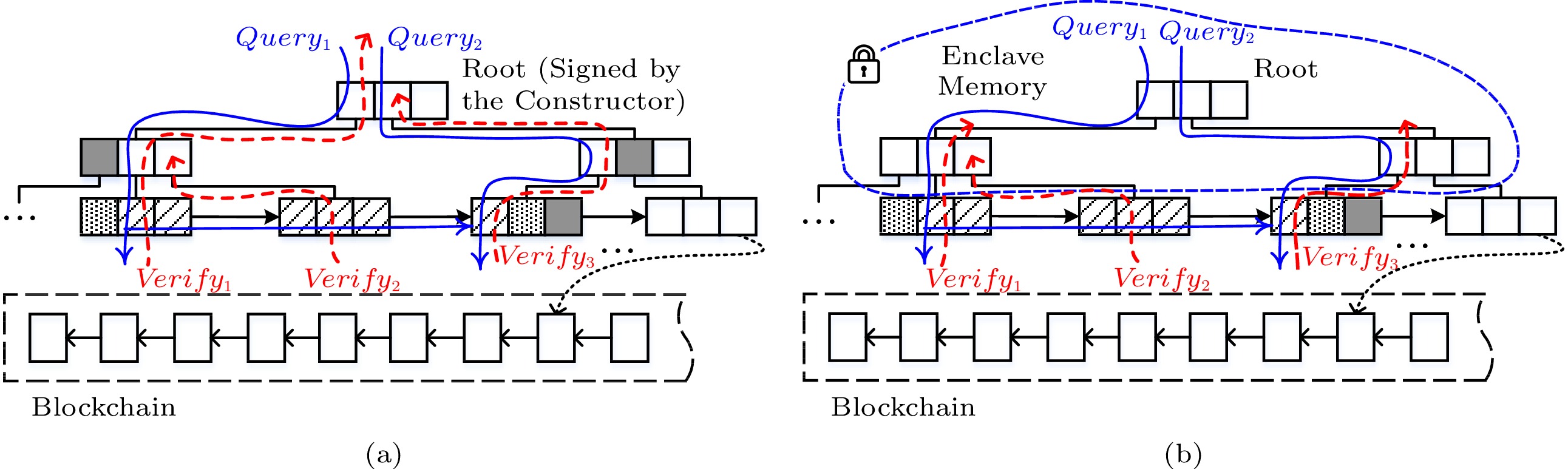
As shown in Fig.4(a), $Query_1$ from the root node to the leaf node adds to the VO all the digests on the left of the query path, and finds query results in leaf nodes. $Query_2$ adds all the digests on the right of the query path. Besides the correctness, the range query also needs to ensure the completeness of query results. Therefore, the VO involves two boundary tuples (point boxes in Fig.4). The two boundary tuples are the left and right boundaries of query results, indicating no tuples are omitted from query endpoints. By restructuring the root digest with the consecutive query results and two boundary tuples, we can check whether all tuples in the query range are involved or not. The authenticated range query needs to verify more VOs because they involve more results, which incurs higher communication cost than the point query. As demonstrated by dash arrows, the results of the range query involve consecutive leaf nodes, i.e., multiple verification paths. For verification, in order to compute the root digest, reconstructing the whole query subtree according to multiple verification paths will induce significant computing cost to light clients.

Figure  4.  Range query and verification on MB-tree. (a) Range query. (b) Range query with Intel SGX.

下载: 全尺寸图片 幻灯片

Since the MB-tree nodes cached in the enclave help to shorten the verification path and reduce the number of nodes to be verified, processing the range query with Intel SGX alleviates the cost of query verification, as illustrated in Fig.4(b). Specifically, when all leaf nodes covered by the query results are in the enclave, it is unnecessary to perform any verification. Thus, the SGX simplifies the query authentication of the MB-tree.

5.2   Join Query with Intel SGX

Similar to standard B-tree, MB-tree^[2] only supports the query attribute on which it is built. In our scheme, to support verifiable queries on multiple attributes, it needs to build an MB-tree for each attribute. Thereby, a disjunctive selection can be processed by combining results from multiple authenticated range queries over their respective MB-trees, and a conjunctive selection can be transformed to an authenticated join query over multiple MB-trees.

For blockchain, join queries integrating on-chain data, or combining on-chain and off-chain data are quite common. Unlike the authenticated range query, the authenticated join query is inherently more complex because the combination of two relations is harder to verify. The most efficient existing solution is the authenticated index merge join (AIM)^[8] that returns intermediate results to the clients who would then verify those results and generate join outputs locally. The generation of join results undoubtedly incurs considerable communication and computing costs to clients. Therefore, if Intel SGX is used to match tuples and generate join outputs, light clients would only need to receive trusted join results. In this subsection, depending on MB-tree and Intel SGX, we present two authenticated join algorithms: Authenticated Merge join (AMJ) and Authenticated Index Nested-Loop Join (AINLJ). The two algorithms focus on pairwise joins of the pattern $R \bowtie_P S$ where $P$ is a predicate with ordering-based operators such as =, $<$lt;$ and $>$gt;$.

5.2.1   Authenticated Merge Join

Like the join query between different tables in the relational database, blockchains also need the join query for different types of transaction data, for instance, the join query $supplier \bowtie order$ between the transactions $supplier$ and $order$ in a blockchain-based supply chain. If two MB-tree indexes on join attributes of two types of transaction data are constructed respectively, search keys in the leaf nodes of the MB-trees are ordered. Therefore, we can directly utilize this feature to implement AMJ in the enclave.

Algorithm 1 illustrates AMJ based on the MB-tree and Intel SGX. $R$ and $S$ can be transaction data or result sets from authenticated range queries. $T_R$ and $T_S$ are MB-trees constructed on $R$ and $S$ respectively. $R_{\rm encl}$ and $S_{\rm encl}$ are available enclave memory allocated to $R$ and $S$ respectively. Due to memory limitations of the enclave, it is infeasible to load all transactions into the enclave. Therefore, function $NextTuple$ loads a batch of leaf nodes of the MB-tree into the enclave, when $R_{\rm encl}$ or $S_{\rm encl}$ is empty. Subsequently, Intel SGX performs the sort-merge scan of these leaf nodes and adds all matching tuples to the result set. For the sort-merge join, sorting is always expensive. The SGX does not need to perform the sorting operation because of the ordered leaf nodes of the MB-tree. To verify the integrity of data read into the enclave, function $NextTuple$ uses leaf nodes in the enclave to incrementally compute the root digest of the MB-tree.

5.2.2   Authenticated Index Nested-Loop Join

Due to the requirement of privacy-preserving and limitation of storage capacity, part of blockchain data is stored off-chain (e.g., databases or dedicated file systems). For example, in a blockchain-based supply chain, only the ${\rm ID}$ of $operator$ is on the blockchain, and the detailed information of $operator$ is stored off-chain. To obtain complete information, we need to perform the join query integrating on-chain and off-chain data (e.g., $operator \bowtie order$). It is not easy to maintain indexes on various types of off-chain data. If off-chain data is unordered, we can implement AINLJ in the enclave by utilizing the MB-tree index of on-chain data. For on-chain data, the MB-tree on the join attribute ensures query integrity. For off-chain data, the signature of the entire data assures data integrity.

Algorithm 2 describes AINLJ based on the MB-tree and Intel SGX. Let $R$ denote an off-chain relation, $T_S$ an MB-tree for on-chain data $S$, and $R_{\rm encl}$ the enclave memory allocated for $R$. To mitigate the negative impact of $ecall$ and $ocall$ of Intel SGX, instead of calling into $R_{\rm encl}$ for each tuple of $R$, we process the tuples in batches so that the cost of enclave calling is amortized over a batch of tuples. Since each batch reads $|R_{\rm encl}|$ tuples into the enclave, there are $\lceil|R|/ |R_{\rm encl}|\rceil$ batches in total. Based on MB-tree $T_S$, the nested-loop join processing is implemented as an extension of the range query. For each tuple $t_R$ in $R_{\rm encl}$, the SGX performs the authenticated range query on $T_S$ to find the tuples matching $t_R$. To ensure the integrity of the join results, the SGX can verify the results of the range query with the root digest of MB-tree $h^{\rm root}_S$. Off-chain data $R$ can be verified based on the signature of $R$.

5.3   AAB-Tree in Intel SGX

Using a traditional MB-tree for the authenticated aggregate query, light clients can only authenticate the correctness and the completeness of the range query, incapable of verifying the correctness of the aggregate result. For this reason, after verifying the result set according to the query range, light clients must aggregate the result set locally. This strategy imposes further complexity to light clients. If the result set is large, it will induce considerable communication and computing costs, linear to the size of the result set, to light clients. When aggregate queries are based on the MB-tree with Intel SGX, the result set can be aggregated in the enclave on the full node, and only the aggregate result is returned to light clients through a secure channel. This scheme alleviates the burden of light clients, but increases the overhead for the space-limited enclave. Therefore, we need an efficient index structure suitable for authenticated aggregate queries. AAB-tree^[6] is such an index with verification cost sub-linear to the result set.

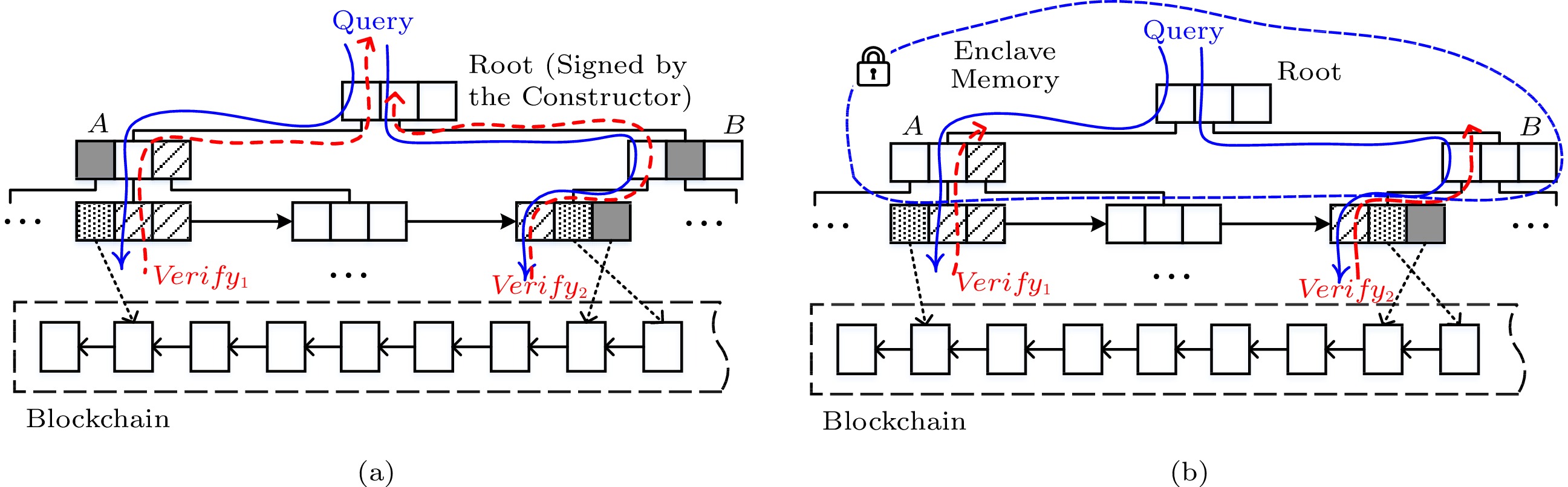
Starting from the root node, the query processor traverses the AAB-tree in a breadth-first manner. When visiting a node, the query processor compares the key range of each entry with the query range: if the key range is within the query range, the entry's aggregate value will be added to the result set; if the key range intersects with the range query, the entry's children will be visited recursively; if the key range and the query range do not intersect, the entry's hash value and aggregate value will be added to the VO. For example, node A has three entries, as shown in Fig.5(a). Since the first entry is outside of the query range, it is only necessary to get the verification information; since the second entry partially overlaps the query range, we continue to traverse for the exact result; since the third entry is inside the query range, we directly retrieve the aggregate value of the entire subtree under the entry without traversing down.

Figure  5.  Aggregate query and verification on AAB-tree. (a) Aggregate query. (b) Aggregate query with Intel SGX.

下载: 全尺寸图片 幻灯片

An AAB-tree occupies less memory footprint than an MB-tree when processing authenticated aggregate queries in the enclave. The pre-aggregated information reserved in each internal node of the AAB-tree can help to answer the aggregate query without traversing the tree all the way down to the leaves. Therefore, as shown in Fig.5(b), without caching low-level nodes, we only need to cache frequently-accessed high-level nodes in the enclave. For some verification paths of the AAB-tree, query verification can start from high-level nodes, not from the leaves, such as the third entry of node A. If the retrieved high-level nodes are all in the enclave, they will not need to be authenticated. In other words, AAB-tree avoids the authentication of low-level nodes, while the SGX avoids that of high-level nodes.

There are three kinds of aggregate queries^[19]: distributive, algebraic and holistic. Except for the holistic aggregate (like MEDIAN), an AAB-tree supports the authentication of the distributive aggregate (like SUM, COUNT, MAX and MIN) and algebraic aggregate (like AVG, expressed as SUM/COUNT), by replacing the aggregate function in each entry. Moreover, the AAB-tree can be extended to deal with the multi-aggregate query. Instead of storing one aggregate value in each entry of a node, we store a list of aggregate values for all necessary aggregate functions.

5.4   Cache Architecture of Query Processing

To improve the efficiency of accessing the MB-tree, we design a three-level storage scheme, including a disk storage, a cold cache and a hot cache, as shown in Fig.6. The disk storage, at the lowest level, persists the entire MB-tree. The cold cache, deployed on the untrusted memory, caches MB-tree nodes to reduce the I/O cost. Hot cache, located on the trusted enclave, only caches frequently-accessed and verified MB-tree nodes to alleviate the verifying cost. We integrate these two types of caches and design an efficient cache replacement strategy.

Figure  6.  Cache architecture of query processing.

下载: 全尺寸图片 幻灯片

When directly applying an LRU cache replacement algorithm to the MB-tree in the enclave, the burst access and sequential scan may load some nodes that are only accessed once into the enclave. However, these nodes will not be swapped out of the enclave in a short time according to the LRU replacement strategy, which lowers the utilization of the enclave memory. Motivated by the LRU-K cache replacement algorithm^[20] that keeps the last K reference times for each page to estimate evicted pages, we propose a replacement algorithm, H-LRU (hierarchical least recently used), for the two-level cache architecture composed of a hot cache and a cold cache. H-LRU considers more of the reference history besides the recent access for each node and addresses the issue of correlated references.

As shown in Algorithm 3, when an MB-tree node is accessed for the first time, it is read out from the disk and buffered in the cold cache, thus avoiding the potential I/O cost in future. Once such a node is accessed again, if that has been quite a while since the last access, i.e., uncorrelated reference, it is promoted to the hot cache, thus eliminating the verifying cost in future. Algorithm 3 uses the following data structure.

● $HIST(n, t)$ denotes the $i$-th most recent access time of node $n$, and does not contain the correlated reference. For example, $HIST(n, 1)$ denotes the most recent access time of node $n$, and $HIST(n, 2)$ the second most recent access time of node $n$.

● $LAST(n)$ records the most recent access time of node $n$, and may be a correlated reference or not.

Compared with H-LRU, LRU may replace frequently referenced pages with pages unlikely to be referenced again. H-LRU moves hot nodes to the enclave and allows infrequently referenced nodes to stay in the regular memory. Cold cache and hot cache call the function $isUncorrelated$ to exclude nodes that are accidentally visited. If that is an uncorrelated reference, the node is promoted to the hot cache and moved to the head of the cache queue since the head has the highest buffer priority. When the hot cache is full, it evicts the least recently used node. When the cold cache is full, it evicts the node whose second-most recent reference is the furthest in the past. Therefore, only the nodes that are frequently accessed for a long time are located in the enclave. Our algorithm considers both recentness and frequency, and avoids the interference of related references, so as to improve the utilization of the enclave memory and achieve better performance.

6.   Batch Updates

For an MB-tree^[2], when a leaf node is updated, the digest change will be propagated up to the root node, which will lock the entire index in the exclusive mode and block other updates and queries. If the entire subtree to be updated is cached in the enclave, the digest changes caused by multiple updates can be combined and written back to the root node at one time so that the update cost can be reduced significantly. In addition, since blockchain periodically submits transactions by block, it is suitable for batch updates.

Since only the signed root node is trusted in a traditional MB-tree, the digest change must be propagated to the root node immediately once a leaf node is updated. When the updates occur frequently, it will significantly downgrade the system performance. With Intel SGX, since all nodes cached by the enclave are verified and trusted as mentioned before, the propagation of a digest change can end at an internal node located in the enclave.

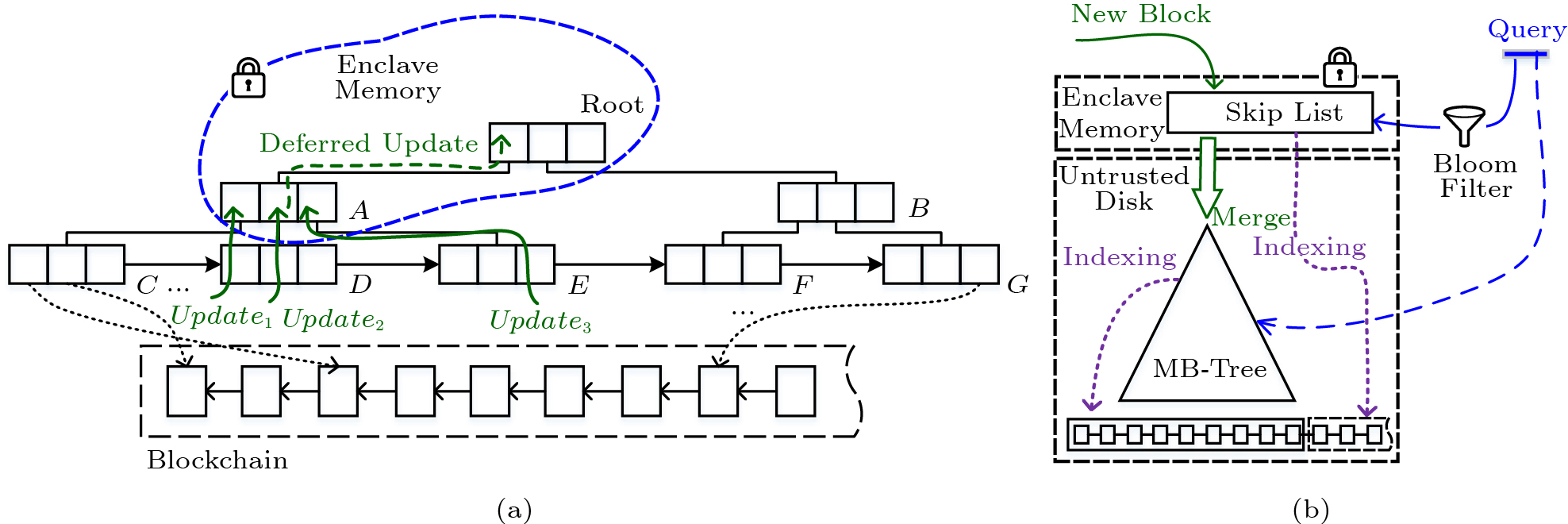
As shown in Fig.7(a), $Update_1$, $Update_2$, and $Update_3$ represent three update operations on different leaf nodes. Since node A in the enclave is trusted, the digest propagation of three updates will be stopped at node A. Once node A is evicted in future, or its structure changes due to the split or merge operation, the deferred digest changes reflecting three updates will be propagated to the root node immediately. The digest of each node is reserved in its parent node. When the digest change of a node is deferred for its parent node, the previous digests in the ancestor nodes will not affect the verification of the other branches^[21]. In Fig.7(a), node A in the enclave does not propagate its digest changes to the root node immediately, which does not affect the verification of the other branches. All subtrees under node A can be verified based on A's current digest. Other branches without node A can be verified with A's previous digest in the root node. In other words, nodes C, D and E can be verified by node A, a trusted root for its subtree; nodes F and G can be verified by the root node.

Figure  7.  Batch update and merge. (a) Deferring digest update. (b) Dual-stage hybrid index.

下载: 全尺寸图片 幻灯片

For an AAB-tree^[6], besides batch updates in leaf nodes, we take an incremental manner to maintain aggregate values in the internal nodes. When a leaf node is updated, besides the digest change, the aggregate change also needs to be propagated up to the root node. If we defer the aggregate change just like deferring the digest change, it will affect the correctness of aggregate queries. The procedure that propagates a change in the leaf node to the root node, essentially visits the same nodes as the search procedure. Therefore, incrementally maintaining the aggregate value of each internal node along the search path can improve update performance, while locating the leaf node for an update operation.

6.1   Batch Updates with Hybrid Index

Besides propagating digest changes, the lock operation for a node update will block query processing and limit concurrency. To alleviate the update cost of the MB-tree, previous work^[2] generally adopts batch updates to defer the installation of a single update and process multiple updates at the same time. Blockchain accumulates multiple transactions in a block and submits them in batches, which is applicable for batch updates.

We present a dual-stage hybrid index architecture. As shown in Fig.7(b), it maintains a skip list in the enclave to buffer multiple new blocks. The skip list, without additional rebalancing cost, is more suitable for the memory index compared with typical balanced trees (e.g., $B^{+}$-tree or red-black tree). Our hybrid index is composed of a skip list and an MB-tree. The skip list, located in the enclave, indexes newly appended blocks, and the MB-tree, located on disk, indexes historical blocks. The query processor searches both the skip list and the MB-tree to get the complete result. Moreover, a bloom filter atop of the skip list is added to speed up searching.

6.2   Merge

The main purpose of applying merge processing is to utilize batch updates to alleviate the cost of digest propagation in the MB-tree. Since blockchain updates data by block, different from the traditional database, we design a more appropriate merge algorithm.

There are two solutions for batch updates in the MB-tree: full rebuild and delta update. Full rebuild merges and reorders existing leaf nodes of the MB-tree with a batch of new transactions, and rebuilds the entire MB-tree. Delta update directly adds new sorted data to the MB-tree in batches. Full rebuild will incur considerable cost to recompute the digests of the entire MB-tree and block queries for a long time. Therefore, delta update is applied to our merge processing, as shown in Algorithm 4.

Our batch update algorithm is efficient because it performs searching and propagates digest changes only once for all updates belonging to the same parent node. When traversing the tree, the algorithm applies the lock-coupling strategy of nodes, which means only the node and its parent are locked exclusively. The parent is kept locked until all child nodes have been updated and the digest changes from them have been applied. For bulk insertions, if a parent node gets full (i.e., the parent node contains $2n$ keys) or all data belonging to a parent node has been inserted, the previously deferred digest changes in the parent node will be propagated back to the root node. After that, restarting from the root node, the algorithm searches a leaf node for next insertion.

To find the corresponding entry for a search key, the function $SearchNode$ starts from the root and traverses all the way to the leaf. If an internal node is full or half full, the split or merge operation is triggered accordingly.

According to which data is moved out of the skip list and merged into the MB-tree, there are two solutions: merge-cold and merge-all. Merge-cold selectively moves infrequently accessed cold data out of the skip list that is used as a write back cache. Merge-all moves all data out of the skip list, and treats the skip list as a write buffer that continuously accumulates new blocks from the blockchain network. Since our system has the hot cache and the cold cache for query processing, and needs to buffer enough new blocks to reduce the MB-tree update cost, merge-all is more suitable.

Moreover, it is important to determine a merge threshold about how many blocks are buffered for one merge processing. If the number of buffered blocks is too small to form a considerable sequence length, the MB-tree update cost will not be reduced drastically. Contrary, too many buffered blocks will take longer to search in the skip list and process merging. Therefore, the specific threshold can be set according to the actual requirement.

7.   Cost Analysis

We compare our scheme with MB-tree^[2] and AAB-tree^[6] in terms of the communication, verification and update costs. The comparison results are summarized in Table 1. The cost of the VO construction in our scheme is the same as that in the traditional scheme. The traditional query verification is performed on the client. Our query verification is processed with Intel SGX on the server, and thus the client does not need to receive or verify any VO.

Table  1.  Cost Comparison

	Communication Cost	Verification Cost	Update Cost
MB-Tree[2]	$|R|+(\log_f{(n_tn_q)})(f-1)|h|$	$(\sum_{i=0}^{(\log_fn_q)-1}f^i+\log_f\frac{n_t}{n_q})C_h+C_v$	$(\log_fn_t)C_h + C_s$
MB-Tree in Intel SGX	$|R|$	$(\sum_{i=0}^{(\log_fn_q)-1}f^i+\log_f\frac{n_t}{n_q})C_h$	$(\log_fn_t)C_h$
AAB-Tree[6]	$|a|+(\log_f{(n_tn_q)})(f-1)(|h|+|a|)$	$(\sum_{i=0}^{(\log_fn_q)-1}f^i+\log_f\frac{n_t}{n_q})C_h+C_v$	$(\log_fn_t)(C_h+C_a)+C_s$
AAB-Tree in Intel SGX	$|a|$	$(\sum_{i=0}^{(\log_fn_q)-1}f^i+\log_f\frac{n_t}{n_q})C_h$	$(\log_fn_t)(C_h+C_a)$
Note: $n_t$ represents the number of tuples; $n_q$ represents the number of tuples in a query result; $f^i$ represents the number of nodes at the $i$-th level of a query subtree; $C_h$ represents the cost per hash operation; $C_v$ represents the cost per verification operation; $C_s$ represents the cost per sign operation; $C_a$ represents the cost per aggregate operation; $R$ represents a query result; $f$ represents the node fanout; $h$ represents a hash value; $a$ represents an aggregate value.

下载: 导出CSV 

| 显示表格

7.1   Cost Analysis of MB-Tree

The VO of the authenticated range query has two parts: 1) the sibling hashes along two boundary paths of the query subtree, with the size of $2(\log_fn_q)$ $(f-1) |h|$ (each entry along the path has at most $f-1$ siblings and $|h|$ is the size of a hash value in bytes), and 2) the sibling hashes along the common path of the query subtree, with the size of $(\log_fn_t-\log_fn_q)(f-1)|h|$. Hence, the VO size is $(\log_f{(n_tn_q)})\times (f-1)|h|$. Since MB-tree contains query results and VOs, and our scheme only requires query results, the communication costs of MB-tree and our scheme are $|R|+(\log_f{(n_tn_q)})(f-1)|h|$ and $|R|$ respectively ($|R|$ is the size of query results in bytes).

The verification of the authenticated range query has three parts: 1) the hashing for the entire query subtree except the common path, with the cost of $(\sum_{i=0}^{(\log_fn_q)-1}f^i)C_h$, 2) the hashing for the common path of the query subtree, with the cost of $(\log_f\frac{n_t}{n_q})C_h$, and 3) the verification of the root signature. Therefore, the verification cost is $(\sum_{i=0}^{(\log_fn_q)-1}f^i+ \log_f\frac{n_t}{n_q})C_h+C_v$. Because our query verification is processed with Intel SGX on the full node, which avoids verifying nodes at upper levels and the root signature, the verification cost is less than or equal to $(\sum_{i=0}^{(\log_f n_q)-1}f^i+\log_f \frac{n_t}{n_q})C_h$.

The update of MB-tree has two steps: 1) re-hashing for every node on the search path, with the cost of $(\log_fn_t)C_h$, and 2) re-signing for the root node. Hence, the update cost is $(\log_fn_t)C_h + C_s$. As our scheme reduces the propagation of digest changes and removes the signing operation for the root node, the update cost is less than or equal to $(\log_fn_t)C_h$.

7.2   Cost Analysis of AAB-Tree

The VO of the authenticated aggregate query has two parts: 1) the sibling hashes and aggregate values along two boundary paths of the query subtree, with the size of $2(\log_fn_q)(f-1)(|h|+|a|)$ ($|a|$ is the size of an aggregate value in bytes), and 2) the sibling hashes and aggregate values along the common path of the query subtree, with the size of $(\log_fn_t-\log_fn_q) (f-1)(|h|+|a|)$. As an AAB-tree commonly only contains VOs from nodes at upper levels, the communication cost is less than or equal to $|a|+(\log_f{(n_tn_q)}) (f-1)(|h|+|a|)$. Our scheme does not contain the VO, and thus the communication cost is the size of an aggregate value.

The verification of the authenticated aggregate query has three parts: 1) the hashing for the entire query subtree except the common path, with the cost of $(\sum_{i=0}^{(\log_fn_q)-1}f^{i})C_h$, 2) the hashing for the common path of the query subtree, with the cost of $(\log_fn_t-\log_fn_q)C_h$, and 3) the verification for the root signature. The AAB-tree computes the aggregate result based on nodes at upper levels in comparison with the MB-tree, which shortens the query and verification path, and our scheme with Intel SGX further shortens the verification path from the nodes at upper levels to the root node. Hence, the verification costs are at most

and

respectively. When a leaf node is updated, AAB-tree needs to propagate both digest changes and aggregation changes from the leaf node to the root node, with recomputing hash values and aggregate values (with the cost of $(\log_fn_t)C_h$ and $(\log_fn_t)C_a$), and re-signing the root node. Our scheme avoids the propagation of digest changes and the root signature. Thus, the update costs are at most $(\log_fn_t)(C_h+C_a)+C_s$ and $(\log_fn_t)(C_h+C_a)$ respectively.

8.   Security Analysis

We perform security analysis in this section. Our basic security model is secure, provided that the underlying hash function is collision-resistant and the security enforcement of Intel SGX cannot be broken.

Tampering Attack. As the frequently-accessed nodes of the MB-tree and the entire skip list are resident in the enclave, attackers cannot tamper with them. Although the other nodes of the MB-tree located in the regular memory may be tampered with by adversaries, the integrity of query results can be verified by the trusted nodes in the enclave. Using the query results and VOs, the query processor reconstructs the digests in a bottom-up fashion until reaching the first cached node, and compares the computed digest against the one reserved in the enclave. In this way, for the case that a node has been successfully tampered with, there exist two MB-trees with different nodes but the same root digest. This implies a successful collision of the underlying hash function, which leads to a contradiction.

Network Attack. In our scheme, the MB-tree ensures the integrity of query results in the application layer, and the transport layer security (TLS) channel assures the integrity of communication data in the network layer. The application layer transmits query results to the network layer through the secure enclave that cannot be accessed by the full node. To protect data transmission between the light client and the secure enclave, the light client can establish a secure TLS channel with the enclave on the full node. Intel SGX's remote attestation ensures that the channel's remote endpoint terminates within the secure enclave. After verifying query results returned by the MB-tree, the SGX sends it from the secure enclave to the light client through the TLS channel. The TLS channel uses 128-bit AES-GCM in the encrypt-then-MAC (message authentication code) mode for symmetric encryption and authentication. The MAC that behaves like a hash function can detect any malicious alteration to the data over the channel. Thereby, a network stack implementation could remain untrusted, as long as a TLS connection on its top terminates inside the trusted enclave. In our system, the AES-GCM only takes about 1 μs to encrypt or decrypt 1 KB data; hence it will not incur expensive cost unless the query result is very large.

Rollback Attack. The support of persistence for the MB-tree requires protection against rollback attacks. In a rollback attack, the untrusted node replaces the MB-tree with an earlier version, so that the client reads stale results. A trusted monotonic counter can ensure the enclave always uses the latest version of an MB-tree. To defend the rollback attack and guarantee the freshness of query results, we can use the Intel SGX monotonic counter service or distributed rollback-protection systems such as ROTE^[22].

Untrusted Blockchain Data. In our scheme, Intel SGX on the full node performs all verification for the light client, yet a dishonest full node may deliver incorrect or incomplete block, and even not send the latest block to the enclave. To protect against such compromises, a light client can acquire the latest block hash from other sources, compares it with that from the SGX, and deduces if the result is integral or not.

9.   Implementation and Evaluation

In this section, we evaluate the performance of our query authentication scheme that contains range and aggregate queries, join processing, cache replacement and batch updates.

9.1   Experimental Setup

We use BChainBench^[13], a mini benchmark for blockchain databases, to generate a synthetic blockchain dataset that consists of 1 million transactions, of which each key has eight bytes and each value has 500 bytes. In our implementation, the page sizes of the MB-tree and the AAB-tree are set to 2 KB. Each entry of the MB-tree occupies 36 bytes (8 bytes for the key, 8 bytes for the pointer and 20 bytes for the digest), so that each node has 56 entries ($\lfloor(2\,048-(8+20))/(8+8+20)\rfloor$ = 56). Each entry of the AAB-tree occupies 44 bytes (8 bytes for the key, 8 bytes for the pointer, 8 bytes for the aggregate value and 20 bytes for the digest), so that each node has 45 entries ($\lfloor(2\,048-(8+8+ 20))/(8+8+8+20)\rfloor$ = 45). Initially, in our scheme, the MB-tree and the AAB-tree are stored on disk, except that the root node is located in the enclave. Intel SGX's EPC is limited to 128 MB whereof only 93 MB are available for usage due to the metadata. Allocating the limited enclave memory is a trade-off between query time and update cost. For the current blockchains, considering their block generation interval and a few thousand transactions per block, we allocate less memory for batch updates. Therefore, 70 MB and 10 MB of the enclave memory are allocated for the hot cache and the skip list respectively, and the rest for the code base. In addition, 1 GB of the regular memory is allocated for the cold cache. All experiments were conducted on a server equipped with 32 GB RAM and Intel Core i7-8700k CPU @2.70Hz, and running Ubuntu 16.04 OS with Intel SGX Linux SDK and SGXSSL library.

9.2   Query Performance

We report the performance of four solutions in the following series of experiments, including MB-tree, AAB-tree, MB-tree in Intel SGX, and AAB-tree in Intel SGX. Note that the former two are traditional solutions while the latter two are based on Intel SGX.

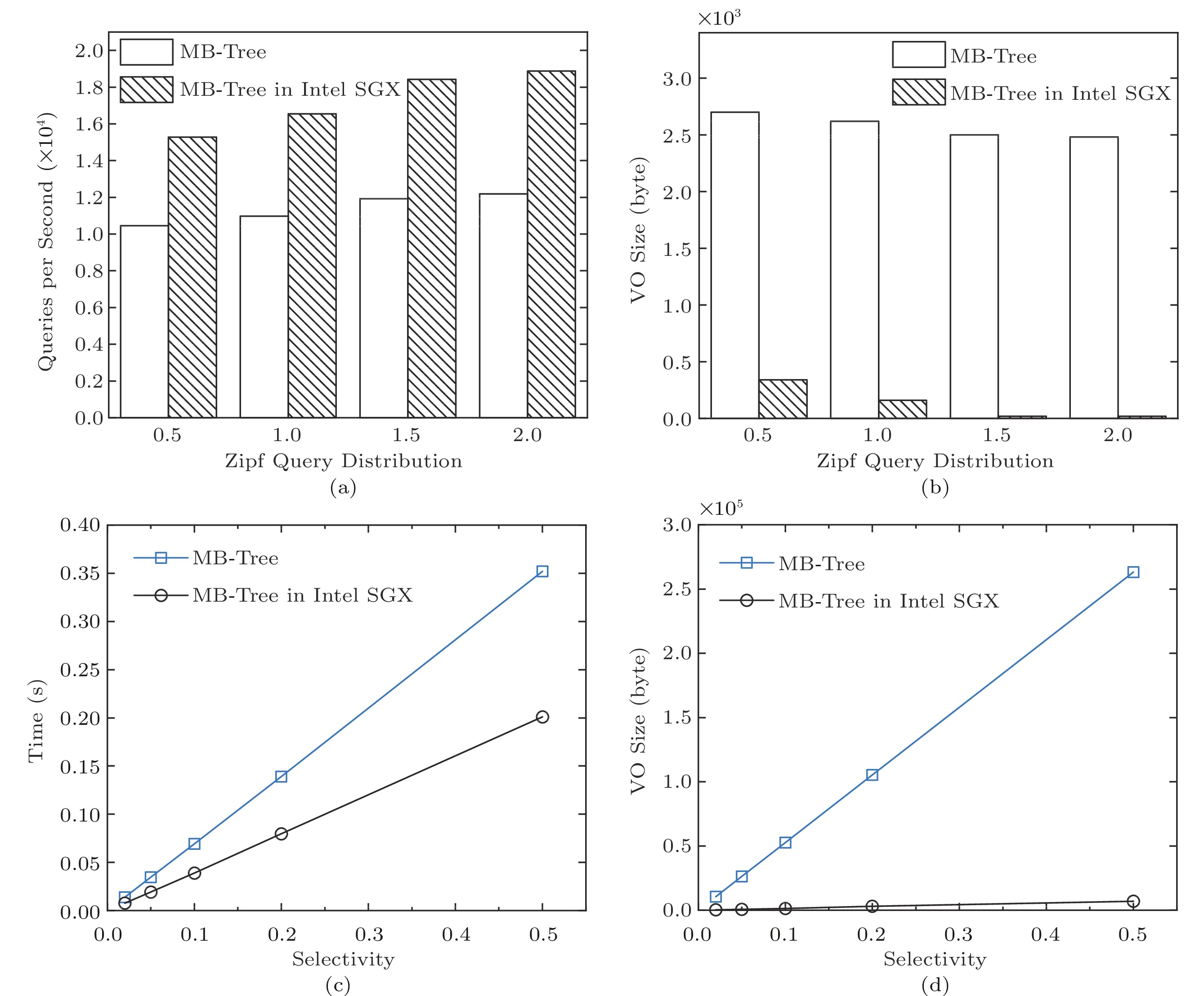
Fig.8(a) manifests the performance of the point query in the Zipfian distribution. With the increment of the skew parameter, the throughput of the MB-tree in Intel SGX is about 1.5 times more than that of the MB-tree solution, because the frequently-accessed MB-tree nodes in the enclave shorten the verification path. In Fig.8(b), the VO size of the MB-tree in Intel SGX decreases by one or two orders of magnitude compared with the traditional solution. For the MB-tree in Intel SGX, the verification is accomplished by the SGX on the full node, so that the light client avoids receiving and processing the VO.

Figure  8.  Query performance and VO size of MB-tree. (a) Point query. (b) VO size of the point query. (c) Range query. (d) VO size of the range query.

下载: 全尺寸图片 幻灯片

Fig.8(c) demonstrates the performance of the range query. The execution time of the MB-tree in Intel SGX is merely 60% of the MB-tree solution. In Fig.8(d), the reduction of the VO size is more remarkable, since the range query has more verification information than the point query. The VO size of the MB-tree solution increases linearly with the query selectivity, which exhibits significant communication and verification costs for light clients, especially for mobile devices.

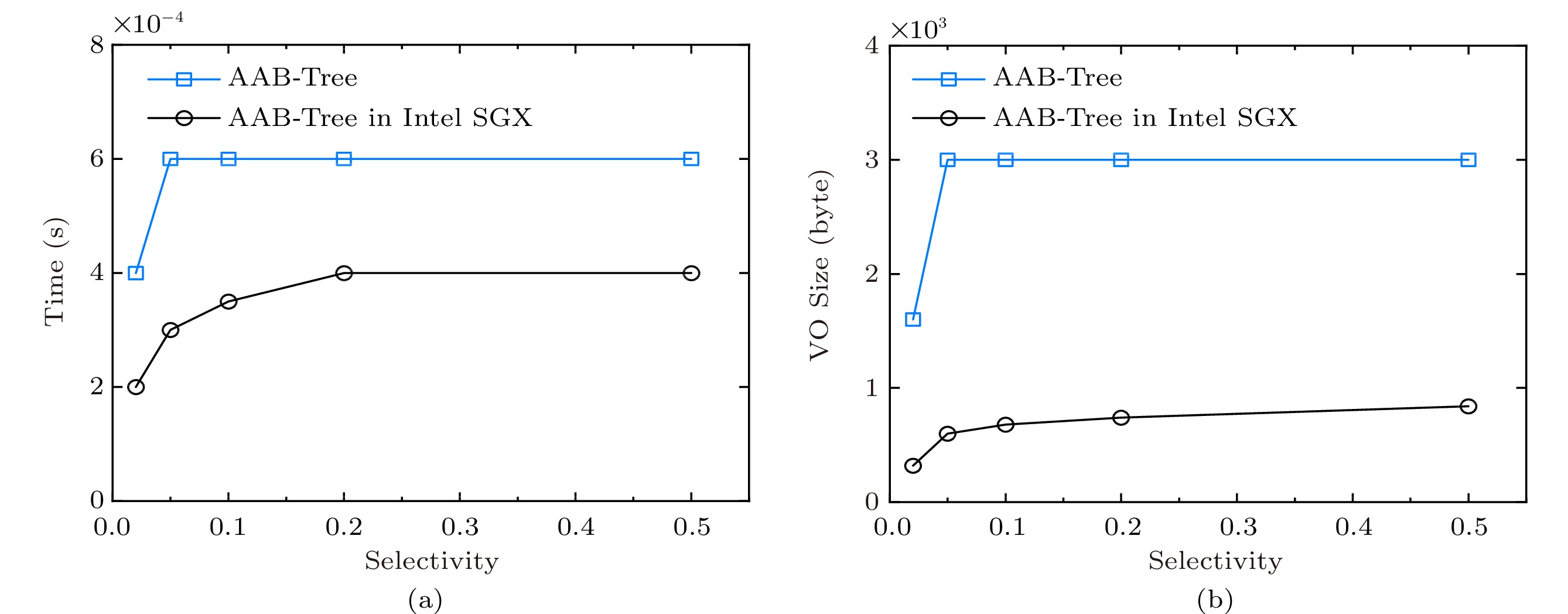
Fig.9(a) shows the aggregate query performance of the AAB-tree. The query time of the AAB-tree in Intel SGX is around 60% of the AAB-tree solution when the selectivity rises from 20% to 50%. In Fig.9(b), the VO size of the AAB-tree in Intel SGX is around 20%–30% of the traditional solution. With the increment of query selectivity, the execution time for aggregate queries tends to be constant, because AAB-tree can retrieve pre-aggregated values directly from high-level nodes without traversing down and performing linear scan on the leaf nodes. The greater the query range, the more the aggregate values in high-level nodes the AAB-tree can utilize, due to a greater aggregation opportunity. By integrating the AAB-tree with Intel SGX, high-level nodes of the AAB-tree are completely cached in the enclave, which further reduces the verification cost. As a result, the AAB-tree solution outperforms the MB-tree solution when processing aggregate queries.

Figure  9.  Query performance and VO size of AAB-tree. (a) Aggregate query. (b) VO size of the aggregate query.

下载: 全尺寸图片 幻灯片

9.3   Join Performance

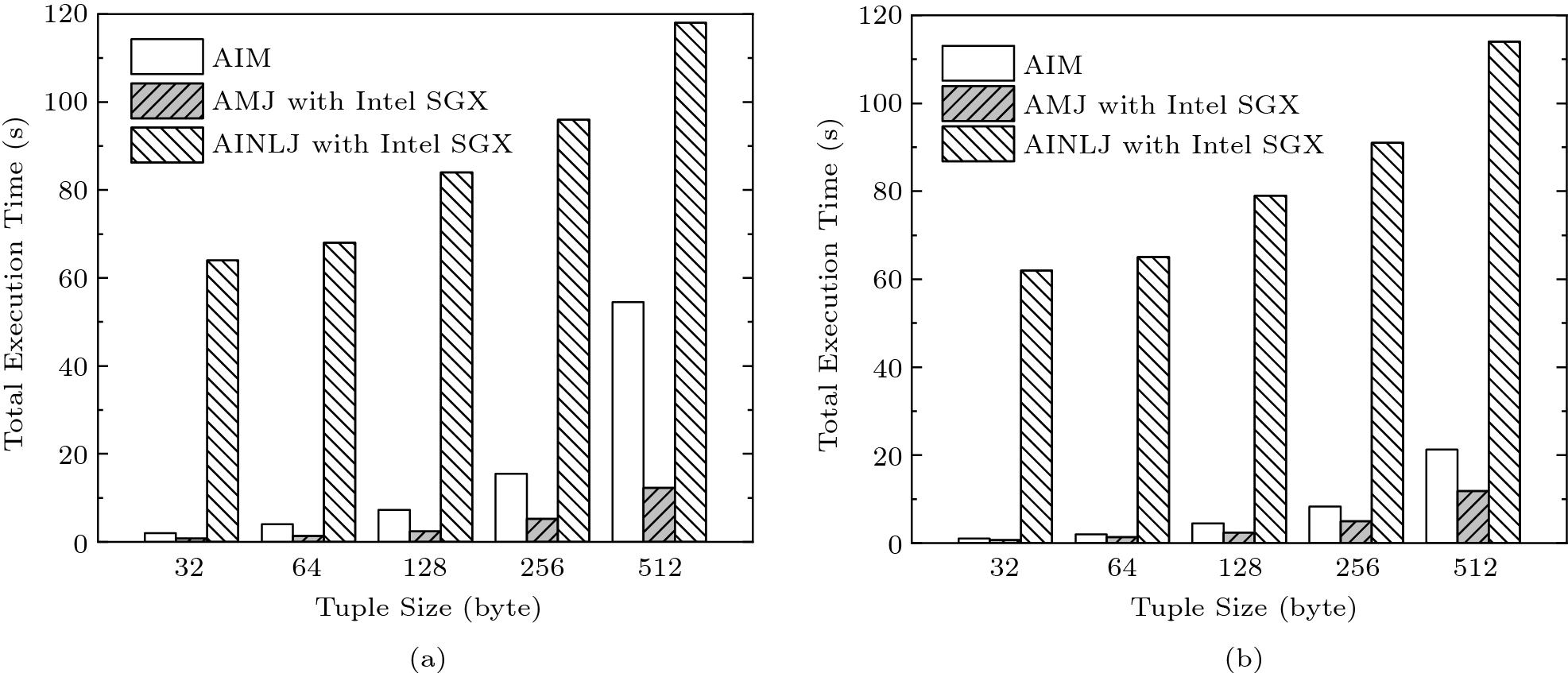
For evaluating the join query we compare the performance of the proposed algorithms (AMJ and AINLJ) against AIM^[8]. The experiment investigates both Foreign Key (FK) and Equi (EQ) joins as in [8]. For the FK join, each tuple in $R$ matches at least one tuple in $S$ due to foreign-key constraint. For the EQ join, both $R$ and $S$ contain unmatched tuples. We use two datasets, each with 1 million tuples and a varying tuple size.

Fig.10(a) displays the execution time of the FK join query for various tuple sizes. The execution time of AMJ is about three times lower than that of AIM. AMJ only needs to perform the authenticated range query once on MB-trees $T_R$ and $T_S$; hence it has less overhead than AIM in verification processing. With the increment of the tuple size, AMJ needs to perform enclave function calls more times to load tuples into the enclave, which increases its execution time. Compared with AMJ, AIM needs to execute the index-traversal multiple times on MB-trees $T_R$ and $T_S$, generating redundant boundary tuples and Merkle proofs for matched or unmatched tuples. The main disadvantage of AIM is that the client needs to receive intermediate results and generate join results locally, which induces considerable burden to the client. AINLJ has the worst performance because it needs to perform the authenticated range query for each tuple in $R$. AINLJ is still a good choice if the off-chain data is small. Fig.10(b) shows the execution time of the EQ join query. The EQ join results in more unmatched tuples compared with the FK join. Because the query results of AMJ and AINLJ only contain matching tuples, the performance is rarely affected by the cardinality of join results. The execution time of AIM is reduced, because it can utilize the MB-tree to prune unmatched tuples from VO.

Figure  10.  Join performance. (a) Foreign key join. (b) Equi join.

下载: 全尺寸图片 幻灯片

9.4   Cache Performance

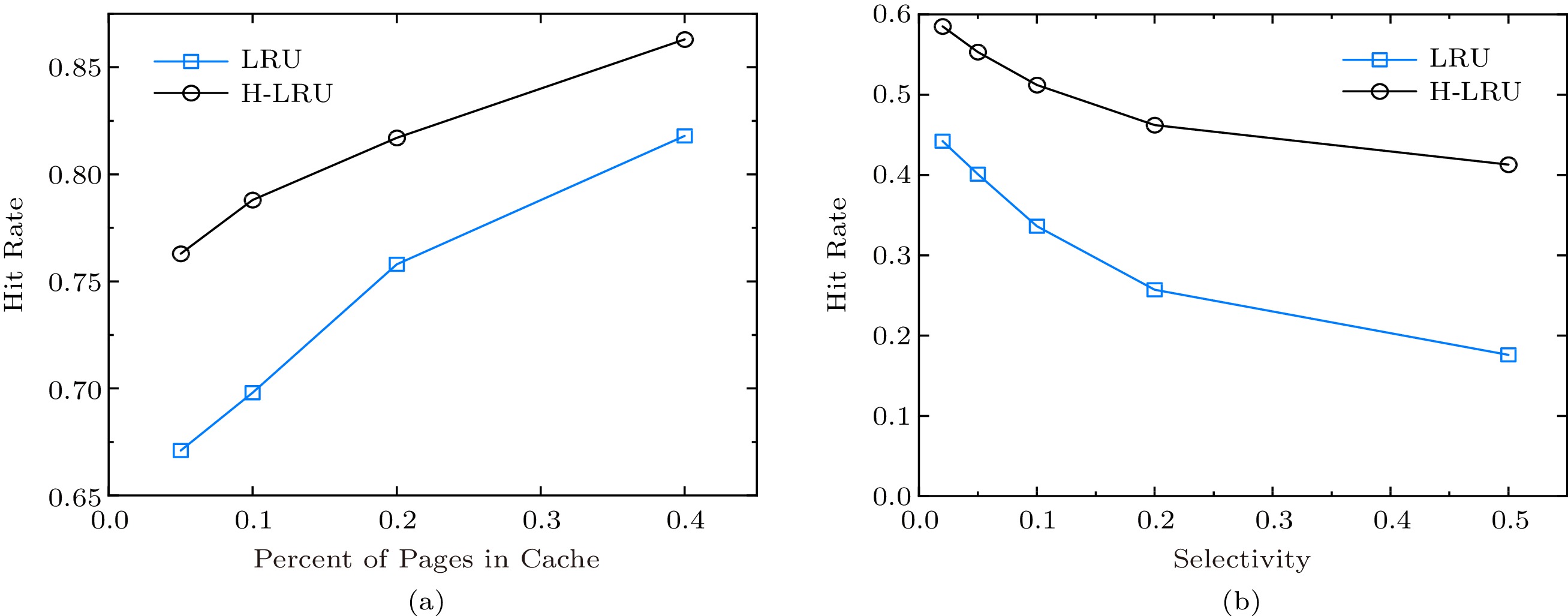
Fig.11(a) reports the performance of H-LRU and LRU. We run 100000 point queries, and report the cache hit rate, i.e., the number of accesses to MB-tree nodes located in the hot cache to the number of accesses to all nodes. We raise the cache size from 5% to 40% of the cache size of the highest hit rate. H-LRU provides about 10% improvement over the traditional LRU. The performance boost is higher with a smaller cache size.

Figure  11.  Effect of H-LRU. (a) Hit rate vs cache size. (b) Hit rate vs selectivity.

下载: 全尺寸图片 幻灯片

In Fig.11(b), we randomly mix some range queries in point queries, which will start scan operations occasionally. We set the probability of starting a range query to 0.1, i.e., 1/10 of the generated queries are range queries. We vary the selectivity based on the cache size of the highest hit rate. The experiments confirm that H-LRU is more adaptable than LRU.

9.5   Update Performance

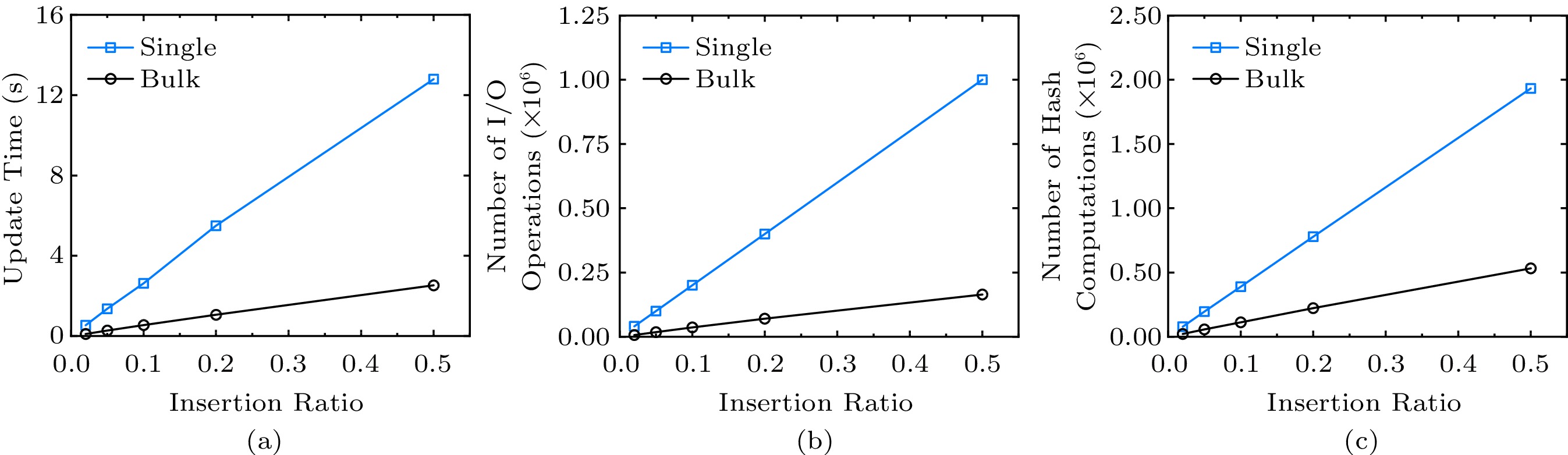
Fig.12 presents the update performance of the MB-tree. The batch update consists of a number of insertions, ranging from 1% to 50% of the blockchain data size. We use the insert-only workload in this experiment because it generates higher merge demand than the update workload. When the insertion ratio reaches 50%, the update time and the number of re-hashing are diminished by about four times, and the number of I/O operations is reduced by about six times. It is because the MB-tree is bulk-loaded with 70% utilization, and bulk insertions quickly lead to many split operations, which creates a lot of new nodes. Although most improvements are contributed by reducing the I/O cost, our batch update algorithm avoids hash computing being propagated to the root node and reduces the lock operations on MB-tree nodes. The MB-tree solution requires expensive signature re-computation for every update. In order to show the update performance of the MB-tree itself, we omit the cost on the signature re-computation.

Figure  12.  Update performance of MB-tree. (a) Update time. (b) I/O operations. (c) Hash computations.

下载: 全尺寸图片 幻灯片

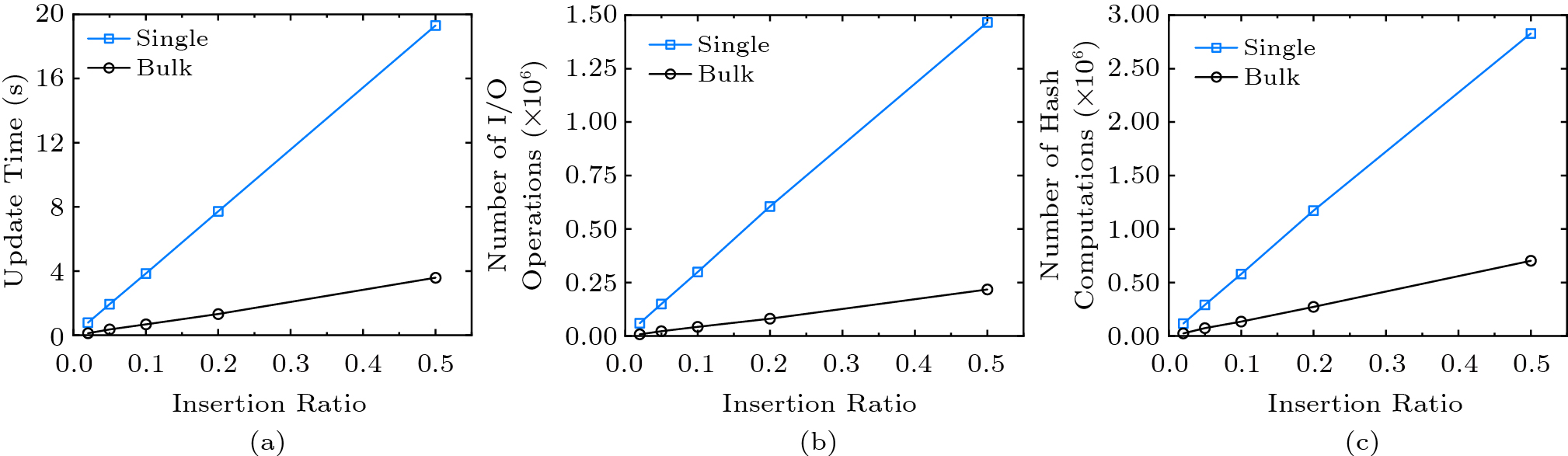
Fig.13 shows the update performance of the AAB-tree. When the insertion ratio reaches 50%, the update time and the number of hash computations are diminished by about five times, and the number of I/O operations is reduced by about seven times. The update performance of the AAB-tree is lower than that of the MB-tree no matter whether it is a single insertion or a bulk insertion, because each entry of an AAB-tree node contains an aggregate value. For the same node size, the AAB-tree has smaller fanout than the MB-tree, which will trigger more split operations. For the single insertion, the AAB-tree has to cope with the propagations of the digest change and the aggregation change at the same time, which incurs a significant cost. For the bulk insertion, the changes of the digests will be propagated up to the root node only after all new data belonging to the same parent node is inserted, which induces reasonable overhead.

Figure  13.  Update performance of AAB-tree. (a) Update time. (b) I/O operations. (c) Hash computations.

下载: 全尺寸图片 幻灯片

10.   Conclusions

We explored the issue of query authentication using Intel SGX for blockchain light clients. Specifically, we integrated MB-tree and Intel SGX, which optimizes the verifiable query performance of blockchains. Compared with the traditional verifiable query scheme, the light client is completely freed from the tedious verification logic by having Intel SGX on the full node handle the query result verification. In addition, we proposed a two-level cache architecture, which alleviates the space limitation of enclave memory. We also designed a batch update method based on a hybrid index structure to reduce the digest update cost of MB-tree. Our scheme can also be used to improve verifiable queries over traditional databases. Security analysis and empirical results substantiated the robustness and the efficiency of our proposed scheme. The VO size of our scheme is reduced by one to two orders of magnitude compared with that of the traditional MB-tree.

Both blockchains and TEE emphasize trust, and therefore we applied hardware-based TEE to blockchains for improving the trust of query processing. In future, we will plan to extend our idea to process other authenticated queries, such as top-k and sliding-window queries.