1.   Introduction

In recent years, underwater imaging systems have been widely used in marine energy exploration, underwater environment monitoring, military applications, and other fields. However, the underwater images^{[1, 2]} suffer from significant visibility degradation mainly caused by the optical transmission properties of water. Hou et al.^[2] proposed an optimization approach to estimate the underwater optical properties, and a set of individual images obtained under different conditions or ranges showed that the degradation is affected by many factors such as turbidity, location, depth, and temperature and is extremely non-linear. Thus, the distance between indistinguishable objects varies accordingly. Moreover, Wells^[3] applied small angle approximations to derive an underwater modulation transfer model and provided a method to compare measurements at different ranges for consistency. The contrast response of an underwater imaging system shows exponential attenuation with the increasing distance between the imaging devices and targets. The recent experimental results in typical sea-water environments^[4] have shown that the objects at a distance greater than 10 meters are almost indistinguishable. Therefore, it is a significant but challenging task to enhance underwater images.

The existing methods for underwater image enhancement can be divided into four classes: restoration methods^[5-8], enhancement methods^[9-13], fusion methods^[14-16], and deep learning methods^[17-19]. Research on restoration mainly focused on the construction of physical models and the utilization of prior information. For example, Chiang and Chen^[6] proposed a method of wavelength compensation that estimates the transmittance by combining a dark channel prior^[7] with an atmospheric scattering model. This method uses triangular bilateral filtering for noise removal and color correction. However, Chiang and Chen's wavelength compensation model is susceptible to the light within the aqueous medium. Recently, Zhang and Peng^[8] have proposed an underwater image formation model, where the medium transmission is estimated for underwater images based on a joint prior. However, the prior information may fail in realistic scenarios, which degrades the robustness of the model. On the other hand, image enhancement methods mainly focus on color correction and contrast enhancement, such as color and contrast enhancement using Retinex-based methods^[9-11], color correction with the white-balance method^[12] and the shade-of-gray method^[13]. Specifically, these Retinex-based methods^{[10, 11]} are based on an assumption of color constancy^[9], that is, the color of the object is determined by the reflection characteristics of the object surface and has only a weak relationship with the irradiation component in the scene. Therefore, the Retinex algorithm^[9-11] can simultaneously achieve state-of-the-art results for contrast improvement and color correction. For example, the multi-scale Retinex (MSR) algorithm^[10] usually uses three fixed-scale filters to estimate the illumination component of the entire image. Moreover, a weighted variational Retinex model^[14] was proposed to estimate the reflectance and illumination under the regularization terms. This model can preserve more details and partially suppress noise. However, the relationship between the imaging depth and the illuminance component is not considered in the weighted variational Retinex model.

On the other hand, Ancuti et al.^[15] proposed a method to restore the underwater degraded images. This method firstly obtains the inputs and the weight measures from the degraded version of the image. Then, four weight maps are developed to increase the visibility of the distant objects degraded due to the medium scattering and absorption. However, this method requires many parameters and considerable post-processing. Moreover, Zosso et al.^[16] proposed a non-local Retinex framework using non-local versions of the sparseness and fidelity priors. Lately, deep learning methods have been applied to enhance underwater images. For instance, Han et al.^[17] provided a systematic review of the state-of-the-art intelligent methods for dehazing and color restoration of underwater images. However, underwater images distorted by either color or some other phenomena lack ground truth, which is a major hindrance towards adopting a similar deep learning approach. Instead of collecting training data, Li et al.^[18] proposed a method named WaterGAN to generate realistic underwater images from in-air images and depth pairings in an unsupervised pipeline used for the color correction of monocular underwater images. Unlike the existing single underwater image enhancement techniques, Berman et al.^[19] considered multiple spectral profiles of different water types and reduced the underwater enhancement problem to single image dehazing. However, since the water type is unknown, this method needs prior evaluation of different parameters of water types. Meanwhile, Li et al.^[20] proposed a real-time visualization system for deep-sea surveying, and Sun et al.^[21] proposed a deep pixel-to-pixel network (DP2P) model by designing an encoding-decoding framework.

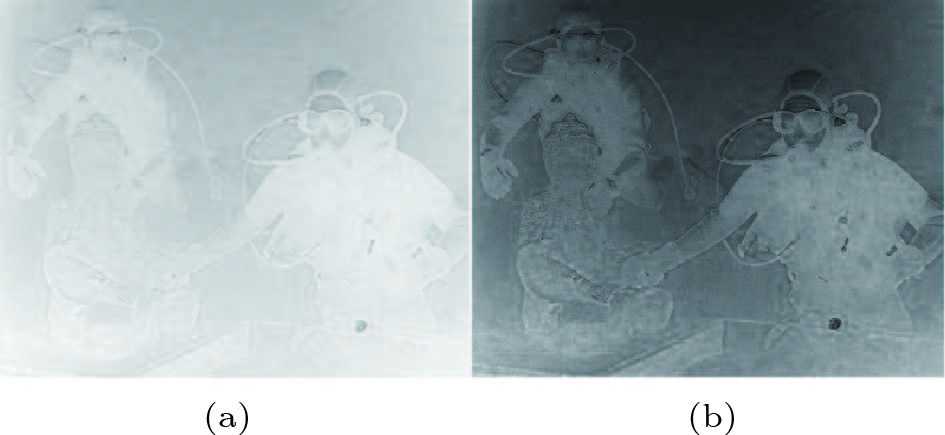
Most of the above-mentioned methods have made significant progress in improving the clarity of underwater images or videos. However, as described in [22, 23], the design of the filter in Retinex-based algorithms, such as the single-scale Retinex (SSR) and the multi-scale Retinex (MSR), does not fully consider the image atomization degree and the image information of different depths of field. Meanwhile, the deep learning methods^{[24, 25]} are almost impossible to obtain prior evaluation of different parameters of water types. In the CLM^[26] method, a wavelength-compensation strategy is hardly to correct the colorcast prior caused by the water depth. Therefore, this wavelength-compensation method is unable to guarantee the color fidelity and the clarity of local details at the same time. Meanwhile, the computational complexity of these variational and fusion methods is very high due to the use of iterative optimization solutions. Thus, it is particularly important to develop an adaptive scale filter, and reduce the complexity of the method. This is the starting point of our research. As shown in Fig.1(b), the MSR method^[10] can enhance the underwater image to a great extent, but the effect of the depth of the field change is neglected when the illumination component is obtained by manually setting the multi-scale filter. Thus, the enhancement result with the MSR method suffers from different degrees of blur. For example, the texture information of the two frogmen at different depths of field is missing. In contrast, the proposed method (as shown in Fig.1(c)) can simultaneously correct color cast and improve the contrast for different depths of field, such as the two frogmen and the Buddha statue.

Figure  1.  Typical underwater image processing results. (a) Original underwater image. (b) Result of the MSR method^[10]. (c) Result of the proposed adaptive full-scale Retinex method.

下载: 全尺寸图片 幻灯片

The rest of this paper is organized as follows. Section 2 presents the proposed model for generating full-scale images and enhancing degraded images. The experimental results and performance evaluations are presented in Section 3. Finally, Section 4 concludes this paper.

2.   Proposed Method

We aim for a simple and robust approach that can increase the visibility of a wide variation of underwater videos and images. To alleviate the aforementioned limitations, an adaptive full-scale Retinex (AFSR) method is proposed to enhance underwater degraded images or videos.

In contrast to previous methods^[9-12] using one or more fixed scales for illumination estimation, we firstly utilize a full-scale design that is guided by optical transmission. Then, we develop a simple strategy based on linear approximations instead of log functions to reduce the computational complexity of the MSR algorithm^[10]. The following Subsections 2.1-2.3 will focus on the related Retinex mode, the adaptive full-scale Retinex, and the framework of the proposed method, respectively.

2.1   Relevance Between Transmission and the Retinex Model

Underwater imaging is mainly affected by absorption and scattering. Absorption is related to the refractive index of the medium, while scattering is caused by the suspended particles and water molecules in the water. According to the Lambert-Beer empirical observation^[1], the propagation of light in media exponentially decays. Assuming that a medium is homogeneous, the optical path transfer function can be expressed as:

where $\beta$ is the attenuation coefficient and d(x) is the depth of the image scene. However, it is not easy to directly obtain these parameter values in actual situations. It is should be noted that this is a priori information closely related to the imaging model. According to the optical imaging model^[2], the light received by the underwater camera consists of direct, forward and background-scattering components. The observed image ${I_\lambda }(x)$ can be expressed as the sum of three components:

where $\lambda$ denotes the optical transmission wavelength, $\otimes$ represents the convolution operator, ${A_\lambda }$ is the illumination of the optical transmission medium and ${J_\lambda }(x)$ denotes the clarity of the image. The two components ${J_\lambda }\left( x \right){t_\lambda }(x) \otimes g(x)$ and ${A_\lambda }\left( {1 - {t_\lambda }(x)} \right)$ lead to fuzzy and color-cast effects since the small-angle scattering comes from the reflected and background light through the suspended particles. Assuming that the distance between the scene and the camera is short, the fuzzy influence caused by forward scattering g(x) can be neglected. (1) can be simplified as follows:

The above-mentioned underwater degradation physical model from (2) is essentially the same as the atmospheric scattering model^[1]. The underwater imaging scenes contain shadows and colored objects or surfaces, which satisfy the conditions of dark channel priors^[9]. Therefore, the underwater light value A and transmission rate t(x) can be obtained by local minimum filtering (i.e., the dark channel prior), and then the enhanced image can be restored. Unfortunately, unlike atmospheric media, the selective absorption of light by water results in different degrees of attenuation at different wavelengths. For example, long red wavelengths are attenuated more than short blue wavelengths. Therefore, using the dark channel method to restore the underwater images will result in serious color distortion. Moreover, the simplified ellipsis also implies that no matter how accurate the transmission rate estimation is, the restoration image will have fog and color deviation. Compared with the transmission models^{[7, 9]}, our method accounts for the assumption of color constancy with Retinex-based methods. As shown in Fig.1(c), the proposed method can remove the color casts while producing a natural vision image.

The Retinex model^[1] assumes color constancy. The color of an object is determined by the reflective characteristics of the surface of the object. From the viewpoint of signal processing, the illumination component of the Retinex changes slowly at low frequencies and the reflection component changes at high frequencies. Thus, the basic model of illumination components can be separated using a Gaussian low-pass filter. The most basic Retinex model is:

where $\lambda$ is one of the RGB channels while ${L}_{i}$ and ${R_i}$ are the illumination and reflection components, respectively. It can be seen that estimating the illumination and reflection components based on the known degraded image signals is essentially an inverse problem. As mentioned in Section 1, there are three ways (path, surround, and variation) to estimate these two components. Considering the reliability and validity of the illumination estimation, our method originates from a surround-function model. The conventional surround-function model is:

where ${F_i}(x,y)$ is a scale surround function. Based on the Retinex model, the reflection component R(x, y) can be obtained using the logarithmic operations under the illumination estimation. Different scales of ${{\rm{\sigma}}_i}$ have different effects. However, the traditional estimation methods^{[12, 13]} rely on experience. In order to improve the model, we use the transmission rate to construct scale parameters. Unlike the transmission model^[7], our method considers color constancy. Unlike multi-scale Retinex, we consider the depth-dependent transmission rate. The proposed method will be derived in detail in Subsection 2.2.

2.2   Adaptive Full-Scale Retinex

We assume that both the Retinex method and the transmission model can achieve the same clarification results, that is, J=R. Since the observations of the two degraded models are identical, we have:

It can be seen from the mathematical model that the optical transmission rate is related to the scale factor. According to (3), the point-to-point mapping relationship between t(x) and ${{\rm{\sigma}}_i}$ can be further calculated. Through the design of scale parameters guided by transmission rates, we can obtain a more accurate model scale. At the same time, the color-constancy prior is integrated so that the proposed model does not require color-balance post-processing alone. We find that the scale is not sensitive to channel attenuation, which proves that the proposed method is more robust than the channel attenuation model^[5].

According to (3), we can further obtain the mapping relationship between t(x) and ${\sigma _i}$. Both sides of this formula are divided by J, and we add a small value so that the denominator will not be 0. We have:

We simplify the left side of (4) as

and obtain the Fourier transformation:

where ${\cal{F}}( \cdot )$ is the Fourier transformation. Thus, we further deduce the analytic function relationship between the scale and the transmission rate as follows:

(5) is an analytic expression based on the frequency that can also be regarded as the representation of the implicit variable t. To directly obtain the spatial domain-mapping relationship between the transmission rate and the full scale, we use the least square fitting method. The final formula is:

where $\theta$ is an exponential coefficient. According to experimental experience, the value of $\theta$ is between 4.30 and 4.95. In this paper, we use 4.7. ${\tilde t_i}$ is the transmission rate that can be obtained by restoration methods^{[7, 9]}. The normal space-domain maps using the transmission rate ${\tilde t_i}$ acquired by the dark method^[7] and the scale parameter ${\sigma _i}$ are shown in Fig.2.

Figure  2.  Normal space-domain results. (a) Transmission rate map. (b) Scale parameter map.

下载: 全尺寸图片 幻灯片

We can see that each pixel's spatial position scale parameter values (Fig.2(b)) are adaptively guided by the transmission rate (Fig.2(a)). Thus, we refer to this method as “adaptive full-scale Retinex”. One advantage of our method is using color constancy, and the other is that the requirement for accurate transmission rates can be relaxed by using an exponential transformation. Therefore, the proposed model is much more robust for underwater image enhancement. Once the values of ${\sigma _i}$ are obtained, the surround function shown in Fig.3 can be deduced.

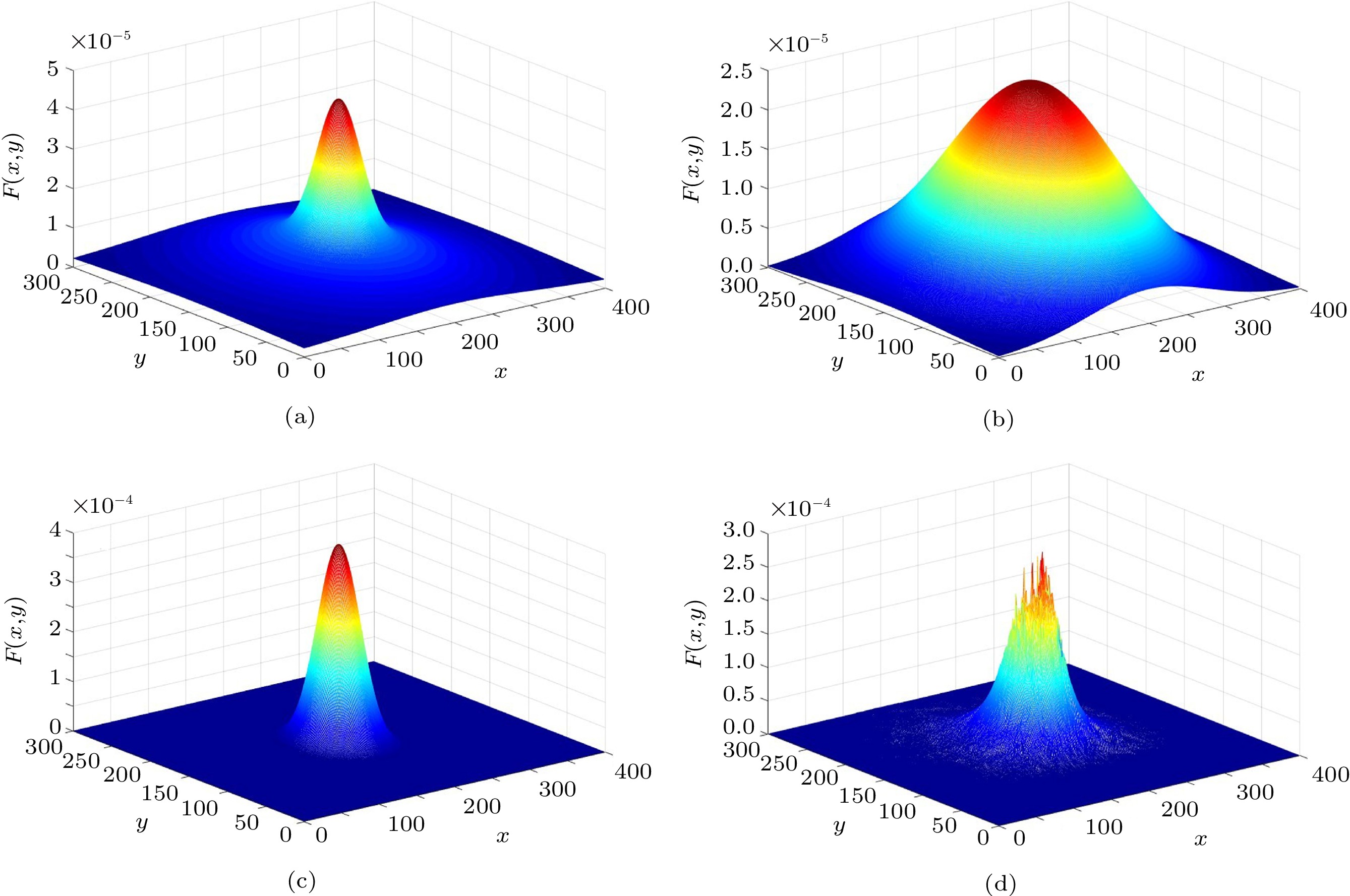
Figure  3.  Scale surround functions under different scale settings. (a) and (b) are spatial surround functions with single scale $\sigma = 60$ and $\sigma = 90$, respectively. (c) The spatial surround function is corresponding to multi-scale $\sigma = 40,80,100$. (d) Proposed full-scale ${\sigma _i}$ that is adaptively guided by optical transmission rates.

下载: 全尺寸图片 幻灯片

As shown in Fig.3, the normalized surround function with different scale parameters presents various attributes. Compared with the SSR (Fig.3(a) and Fig.3(b)) and MSR (Fig.3(c)), the proposed method (Fig.3(d)) takes full account of the depth information, and can adapt to the scene of uneven illumination and inhomogeneous optical-transmission media. According to the scale surround functions under different scale settings, we can see that the proposed full-scale ${\sigma _i}$ is adaptively guided by optical transmission rates. The image enhancement results (Fig.1) also demonstrate the effectiveness of our method.

2.3   Algorithm Framework

Our method extends the conventional Retinex-based enhancement methods^[9-11], and the proposed framework blends the adaptive full-scale filters guided by transmission models. Since color constancy is assumed in Retinex-based methods (in both natural and artificial illumination scenes), the influence of these optical absorbance effects and back-scattering components can be easily reduced. The block diagram of the proposed method is illustrated in Fig.4.

Figure  4.  Block diagram of our proposed method.

下载: 全尺寸图片 幻灯片

Firstly, we obtain the transmittance values ${\tilde t_i}$ with a restored model. Secondly, the full-scale surround function is constructed with the scale parameter ${\sigma _i}$. Thirdly, the illumination and reflection components are obtained using the Retinex model. Fourthly, multiple scenes of underwater images are clarified. Subsection 2.4 will further refine the model.

2.4   Retinex Algorithm Improvement

We theoretically and experimentally analyze the robustness of the proposed framework and optimize the computational time complexity.

2.4.1   Sensitivity Analysis

We can obtain the scale parameter ${\sigma _i}$ guided by transmission rate t_i, which theoretically demonstrates that the scale parameters are not sensitive to different transmission rates during each channel. At the same time, the scale parameter corresponds to the weight of the pixels in the spatial position, while the estimation deviation of the transmission rate affects only the boundary value in the scale space. In other words, the estimation deviation affects only the spatial edges with the smallest weights. Therefore, it can be deduced theoretically that the scale parameter is insensitive to the transmission rate. For further experiments, we use the dark channel method^[9] to calculate the scale parameters and compare it with the ARC^[5] method. Naturally, since the ARC method accounts for different channel transmission rates in underwater image processes, we first use this ARC method to obtain J. Thus, this model is:

where

Interestingly, when the three transmission rates are the same, this ARC^[5] method degenerates to the dark channel method^[9]. The transmission rates, the scale values, and the corresponding residual graphs are shown in Fig.5.

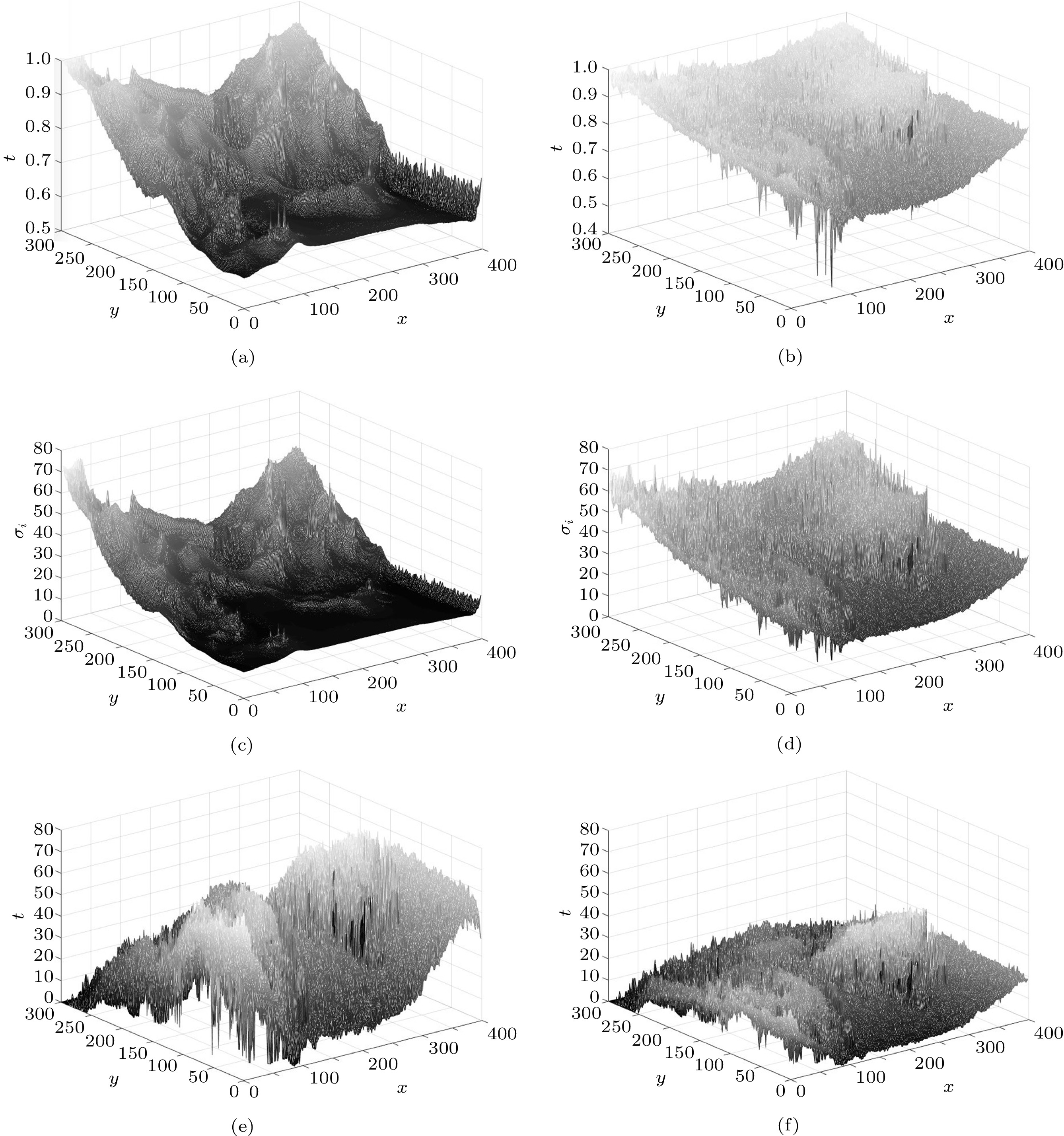
Figure  5.  Analysis results of our method. (a) and (b) are the transmission rate (t) of the ARC method^[5] and our method, respectively, while (c)(d) and (e)(f) correspond to the scale values and the transmission rate residuals of these two methods, respectively.

下载: 全尺寸图片 幻灯片

Since the ARC method uses different proportions of channel transmission rates, the obtained transmission rates and scales are much smoother than the results of our method, as shown in Figs.5(a)–5(d). This smoothing effect ignores some details. Furthermore, according to the normalized residual graphs in Figs.5(e)–5(f), the fluctuation error corresponding to the transmission rate is much larger than the mapping scale fluctuation of the proposed method. In other words, the estimation of scale parameters has a weak relationship with each channel. Thus, the proposed method does not need to separately deal with the transmission rate compared with the ARC method. The ARC method requires high precise transmission rate estimation, but our method can recover well when this estimation value is not very accurate. The advantages of our method are that it increases the robustness of the red-channel algorithm^[5], while providing support for parallel computing. Next, we will further optimize the algorithm.

2.4.2   Algorithm Optimization

After the illumination component is obtained, the reflection component can be obtained by the traditional logarithmic operation. However, since logarithmic operations are non-linear, the computational complexity is high. To address this problem, we develop a quantitative method that directly calculates the reflection component using the mapping function of mean and squared errors.

${{{R}}^{\rm C}}$ is defined as the reflection component without the logarithmic operation, and ${{R}}_{{\rm{mean}}}^C$ and ${{R}}_{\rm{var} }^C$ are the mean value and the mean square error (MSE) in the R, G, B channel, respectively. Thus, the maximum and the minimum of each channel are calculated as:

where $\mu$ is an empirical parameter to control the dynamic adjustment of the image. In our experience, it is set to 3.0. Then, the quantitative mapping function for replacing the logarithmic operations is:

where ${{R}}_{{\rm{opt}}}^{\rm C}$ is the final reflection component that represents the enhanced-clarity images. Once the illumination component is obtained by the AFSR in Section 2, the reflection component is obtained by the proposed quantitative function.

3.   Experimental Results and Analysis

Experiments are performed using Matlab2014bon a PC with Intel Core i7 CPU 2.23 GHZ and 8 GB RAM. In our method, only the empirical parameter $\mu$ is set to 3.0. As described in Section 1, we compare the proposed model with other eight state-of-the-art methods of underwater image clarification. The parameters used in the compared methods are set to be optimal according to the original models. Images captured in different underwater environments often show various degrees of attenuation and degradation, which leads to strong performance for several certain underwater environment conditions, but weak performance for others. Like the previous methods^{[7, 15, 22]}, the experiment datasets are derived from four representational real scenarios, which represent different depths and varying degrees of color cast. Quantitative and qualitative metrics are utilized to compare the restoration performance of these methods.

3.1   Evaluation Metrics

We employ several basic underwater image-quality metrics to evaluate and analyze the performance of different underwater imaging methods, including entropy (EN), standard deviation (SD), and edge intensity (EI). Generally, the standard deviation of an image reflects its high-frequency component, which is related to the image contrast. The higher the standard deviation is, the higher the contrast is, and the greater the color information is. Meanwhile, the entropy represents the amount of information, and the edge intensity describes the degree of edge details of the image. The edge intensity is calculated using the fast Sobel operator^[27]. However, these basic metrics cannot provide a comprehensive evaluation, since underwater images suffer various degradations, and each of them has its own features. Thus, we introduce the underwater image quality metrics measurement (UIQM)^{[28, 29]} to achieve a comprehensive evaluation.

The UIQM is composed of three independent measurements: the underwater image colorfulness measure (UICM), the underwater image sharpness measure (UISM), and the underwater image contrast measure (UIConM)^[29]. The UICM is utilized to evaluate the performance of underwater image enhancement algorithms^{[13, 15, 19]}, and the Red-Green (YG) and Yellow-Blue (YB) color components are used. The overall colorfulness coefficient metric used for measuring underwater image colorfulness can be expressed as:

where RG=R–G and YB=(R+G)/2–B. In order to measure the sharpness, the Sobel operator is first applied to each color component to generate the edge maps. Then the obtained edge maps are multiplied by the original color component to calculate the gray-scale edge maps. By doing this more efficiently, enhancement measure estimation (EME)^[17] is utilized to measure the sharpness:

where the image is divided into blocks and (m, n) is the size of the block, and we obtain the maximal and minimal pixel values in each block. The argument of the logarithmic function indicates the relative contrast ratio within each block. Then the UISM can be written as:

where ${\gamma _{\rm{c}}}$ is the weight coefficient of each color channel (C), normally set to 0.299, 0.587 and 0.114 for R, G and B channels, respectively.

The contrast performance can be measured by the logarithmic measurement as:

It has been demonstrated that underwater images can be modeled as linear superpositions of absorbed and scattered components^[29].

Meanwhile, the water absorption and backscatter by dusk-like particles may cause color casting, sharpness attenuation and contrast degradation. Therefore, it is reasonable to use the linear model to generate the overall underwater image quality measure. Thus, the UIQM is defined as:

where the colorfulness, sharpness and contrast measure are combined together through the linear function designed above, and $\alpha ,\beta ,\eta$ are the weight coefficients to control the importance of each measure and balance their values. Generally, these parameters are set as $\alpha = 0.028\,2,\beta = 0.295\,3,\eta = 3.575\,3$.

3.2   Performance Evaluation

We perform experiments in four scenarios with different color casts and compare them with eight state-of-the-art methods. The experimental results in each scenario are analyzed subjectively and objectively.

We see that on the diver image scene, the DP2P^[21] method fails to correct the color cast, while the Shade^[13] method shows poor contrast enhancement and the restored results generated by the other five methods achieve proper color correction and contrast enhancement. Meanwhile, the WaterGAN^[18] and HL^[19] methods show more consistent color, with reduced effects of vignetting and attenuation compared with the other methods. However, these results could be improved by adding a parameter that adjusts the center position of the vignetting pattern over the image. This demonstrates a limitation of augmented generators. For this diver scene, our method integrally achieves the best performance, although some information loss exists. Our method not only achieves excellent performance for heavy color-casting images, like the diver image in Fig.6(a), but also performs well on images captured in different underwater environments.

Figure  6.  Image clarity results of four different underwater scenes using nine methods (part 1: four methods). (a) Original image including four different scenes of diver, coral, tank, and abysmal rock. (b)–(e) are image clarity results of four state-of-the-art methods corresponding to (b) ARC^[5], (c) Shade^[13], (d) Fusion^[15], and (e) WaterGAN^[18]. By visual comparison, our AFSR method yields comparable or better results of image contrast enhancement, color cast correction and clarity.

下载: 全尺寸图片 幻灯片

The coral scene clarity results in Fig.6 and Fig.7 show that DP2P^[21] and CLM^[26] fail to correct and enhance the visibility of the degraded image, while the other six methods^{[5, 13, 15, 18, 19,22]} show various degrees of improvement of color correction and proper contrast enhancement. As shown in Fig.6(d), the Fusion^[15] method obtains the best visual performance in the mildly degraded scene. Since the deep learning methods are limited by the choice of augmentation functions, augmented generators may not fully capture all aspects of a complex nonlinear model^[18]. Our method obtains better results than the other methods except for the Fusion^[15] method. However, compared with the Fusion method, which uses white balancing and multi-scale line filters, the proposed method does not need any post-processing.

Figure  7.  Image clarity results of four different underwater scenes using nine methods (part 2: the other methods). (a)–(b) are image clarity results of five state-of-the-art methods corresponding to (a) HL^[19], (b) DP2P^[21], (c) VRM^[22], (d) CLM^[26], and (e) AFSR. By visual comparison, our AFSR method yields comparable or better results of image contrast enhancement, color cast correction and clarity.

下载: 全尺寸图片 幻灯片

Among these methods applied to the tank scene, we can see that the DP2P^[21] and CLM^[26] methods over-enhance the distorted image but the Shade method^[13] under-enhances, causing severe color distortions and non-normal contrast enhancement. The other five methods^{[5, 15, 18, 19, 22]} have the successful integral performance of the enhanced image. The ARC^[5] solves the effect of contrast degradation to some degree, but it still tends to be bluish, while the Fusion^[15] method obtains satisfactory results for color correction but has relatively low contrast. By comparison, our method and the WaterGAN^[18] method can achieve both contrast enhancement and color correction. Meanwhile, the edge region of the tank is over-enhanced, and the background color tends to be bluish in the HL^[19] method and VRM^[22] method.

In the deep-sea scene of the abysmal rocks, we can see that WaterGAN^[18] and HL^[19] , and the other methods fail to solve the color-cast issue of the bluish image except for the Fusion^[15] method. Although the Fusion^[15] method outperforms our method in the mean value, our method still performs the best among all these methods. The proposed method has excellent visual performance as well as good RGB color-space mapping and high-contrast degrees but has degraded edge information due to the information loss.

On the other hand, we also use some quantitative indices to compare these methods. As shown in Table 1 and Table 2, these eight non-reference evaluation indices are all scalar values. The larger the value, the better the image quality. According to the comprehensive assessment index and the objective visual performance, the results obtained by our method are better than or comparable to the other methods’ results. The processing time of each competing method is shown in Table 3. For a frame of 300 × 399 × 3, our proposed method takes about 0.017 seconds to calculate the full-scale parameters while the enhancement process only requires 0.021 s. In other words, video sequences with no need for calculating the full-scale parameters (i.e., the first frame can be achieved) can reach the real-time requirements for video processing (less than 0.04 s).

Table  1.  Comparison of Enhancement Results Using General Metrics

Method	EN					SD					EI
	Diver	Coral	Tank	Abysmal Rock		Diver	Coral	Tank	Abysmal Rock		Diver	Coral	Tank	Abysmal Rock
Original image	2.0413	3.0562	4.0213	3.0201		0.0094	0.1320	0.1422	0.0975		0.0441	0.0845	0.0703	0.0746
ARC[5]	6.4221	8.3010	8.9254	5.9874		0.0200	0.2501	0.3521	0.0201		0.0998	0.1907	0.1433	0.1558
Shade[13]	4.0132	6.5408	5.9021	5.0231		0.0115	0.1695	0.2465	0.1540		0.0641	0.0988	1.0200	0.1602
Fusion[15]	6.7021	9.0103	10.0040	6.9421		0.0221	0.3524	0.4020	0.0247		0.1091	0.2201	0.1635	0.1878
WaterGAN[18]	6.7002	8.4013	10.1236	6.8741		0.0204	0.3435	0.4010	0.2460		0.1204	0.2194	0.1647	0.1705
HL[19]	5.8413	8.7956	9.4647	5.4620		0.0136	0.2714	0.3017	0.1731		0.1078	0.1795	0.1421	0.1493
DP2P[21]	3.5761	6.3410	6.3102	4.5822		0.0101	0.1708	0.2011	0.1044		0.0560	0.0987	0.0945	0.1432
VRM[22]	6.5210	8.2514	10.1250	6.9500		0.0175	0.2921	0.3470	0.0195		0.1123	0.2010	0.1547	0.1694
CLM[26]	4.1210	6.5231	6.4203	5.0011		0.0191	0.1802	0.2854	0.1721		0.0757	0.1030	1.2321	0.1567
Our method	6.7817	8.9241	10.1201	7.0320		0.0223	0.3412	0.4021	0.2540		0.1256	0.2168	0.1747	0.1920
Note: Bold numbers represent the maximum value in each column.

下载: 导出CSV 

| 显示表格

Table  2.  Comparison of the Enhancement Results Using Special Underwater Metrics

Method	UICM					UISM					UIConM					UIQM
	Diver	Coral	Tank	A.R*		Diver	Coral	Tank	A.R*		Diver	Coral	Tank	A.R*		Diver	Coral	Tank	A.R*
Original image	0.28	0.36	0.42	0.30		5.03	7.54	8.36	6.44		0.04	0.10	0.21	0.09		1.64	2.59	3.23	2.23
ARC[5]	0.40	0.44	0.67	0.34		9.04	9.34	12.65	7.18		0.12	0.18	0.42	0.10		3.11	3.41	5.26	2.49
Shade[13]	0.33	0.41	0.55	0.38		7.21	9.02	10.77	7.15		0.06	0.19	0.37	0.11		2.35	3.35	4.52	2.52
Fusion[15]	0.39	0.53	0.71	0.52		9.03	11.81	13.16	9.01		0.09	0.24	0.45	0.18		3.00	4.28	5.52	3.32
WaterGAN[18]	0.46	0.50	0.70	0.53		9.10	11.02	13.02	8.95		0.10	0.20	0.48	0.17		3.12	4.17	5.48	3.28
HL[19]	0.40	0.45	0.62	0.37		8.75	9.98	10.97	8.34		0.13	0.22	0.39	0.14		3.04	4.07	5.35	3.04
DP2P[21]	0.31	0.40	0.54	0.36		7.70	11.33	10.98	8.49		0.07	0.16	0.31	0.13		2.53	3.93	4.37	2.98
VRM[22]	0.46	0.51	0.70	0.50		9.01	10.98	13.00	9.04		0.10	0.22	0.46	0.18		3.03	4.04	5.50	3.33
CLM[26]	0.37	0.49	0.57	0.48		8.97	10.90	12.78	8.07		0.08	0.20	0.44	0.17		2.95	3.95	5.36	3.00
Our method	0.47	0.53	0.69	0.55		9.13	11.69	13.01	9.08		0.12	0.21	0.47	0.19		3.14	4.22	5.54	3.38
Note: A.R* stands for abysmal rock.

下载: 导出CSV 

| 显示表格

Table  3.  Processing Time (s/frame) of Competing Methods with Different Frame Sizes

Method	Frame Size
	300 × 399 × 3	720 × 576 × 3
ARC[5]	2.010	4.230
Shade[13]	0.460	1.080
Fusion[15]	9.900	15.310
WaterGAN[18]	2.460	4.020
HL[19]	9.310	13.480
DP2P[21]	0.047	0.065
VRM[22]	0.870	1.130
CLM[26]	1.820	3.480
Our method	0.038	0.052

下载: 导出CSV 

| 显示表格

From the above enhancement results in the four scenes, we can conclude that ARC^[5] and Shade^{[5, 13]} are not suitable for dense color-casting and heavy hazy situations. Meanwhile, methods of [15, 18, 19, 22] perform well in both the tank and coral images, but their performance is degraded for heavy color-cast scenes, such as heavily bluish and greenish images. To further increase the network robustness and enable the generalization to more application scenarios, the WaterGAN^[18] method needs to train the GAN network across more datasets covering a larger variety of environmental conditions. However, underwater images have no ground truth, making it difficult to acquire the training data. Our method and the fusion method^[15] can achieve contrast enhancement and color correction. However, the proposed method is insensitive to illumination and has no over- or under-enhancement like Shade^[13] and CLM^[26]. In addition, the low computational overhead is also a prominent advantage of the proposed method.

3.3   Extensible Application

In addition, the proposed approach can enhance other kinds of degraded images, including those with color distortion or resolution degradation, such as strong fog and backlight images. Fig.8 shows our experimental results of a backlight image. Compared with the state-of-the-art typical methods^{[10, 19, 22]}, our method still performs the best with respect to contrast enhancement, color correction, details, and visibility. In general, it demonstrates the specific application capability of our method.

Figure  8.  Clarity results of degraded backlight images. (a) Original backlight image. (b) MSR^[10]. (c) HL^[19]. (d) VRM^[22]. (e) AFSR.

下载: 全尺寸图片 幻灯片

4.   Conclusions

In this work, we proposed a novel adaptive full-scale Retinex (AFSR) method for underwater image enhancement that tackles both color cast and visibility loss. Our work extends the multi-scale Retinex method^[10], adapting to perform well in scenes with varying illumination and depth, and avoids color artifacts that can appear due to incorrect depth estimation. Among different images, regardless of different underwater imaging conditions, the experimental results demonstrated that our approach obtains better performance than the other eight state-of-the-art methods for contrast enhancement and color cast. Compared with the other methods that “cascade” restoration (individual steps for correcting color and contrast issues), the proposed method can simultaneously correct the color cast and contrast without post-processing. Moreover, the proposed quantitative method that directly calculates the reflection component using the linear mapping function instead of the logarithmic operations can effectively reduce computational complexity. Under the temporal correlations for video sequences, the proposed method can achieve real-time enhancement processing.

In the future, we will combine the proposed image clarification technique with other applications, such as post-processing in membrane diffractive imaging systems, object recognition and detection.