1.   Introduction

The rapid advancement in computing technology has changed the lifestyle of human society. The wide adaptation of mobile devices, wireless communications, and Internet of Things (IoT) has not only improved the quality of life but also changed the landscape of computing. Traditionally, computers are designed for computing, meaning crunching numbers. A scientific simulation can run a program loop many times before it converges, where computing power means the power of number crunching. Internet applications, such as social networks, online search, and other big data applications, are very different. They require massive data movement, collection, and management but little number crunching. Based on the infamous memory-wall problem^[1], the memory system is a weak point of computing systems. Big data applications have put even more pressure on the already lagging memory system, making it the most concerned performance bottleneck of computing at the current time. Improving data access time is a generally agreed research issue facing the computing community today. Intensive research has been done through the years, from developing fast hardware memory devices to optimizing existing memory systems, and from embedding processing in memory to building totally different data-centric computer architecture. But the memory-wall problem remains unsolved and is getting worse.

In [1], Wulf and McKee observed that the performance gap between CPU and memory becomes larger and larger, which is referred to as the memory-wall problem. Before the memory-wall problem, in 1990 the memory-bounded model stated that memory is the bound of computing when the problem size is large^{[2, 3]}. The memory-bounded model compounded with the memory-wall problem, and then compounded with the surging of big data applications, it easily makes the memory system the most concerned performance bottleneck of a computing system. To make it worse, the conventional computing system design principles were developed in the 1960s and 1970s. They are computing-centric and optimized for CPU utilization and performance. To lift memory systems as a primary performance concern may require a total rethinking of computer system designs, including the rethinking of computer architecture and operating system designs. That is an uneasy task. In this paper, we will review the concept of the memory-bounded speedup model, study its relationship with the memory-wall problem, investigate how it has been used in practice to reduce memory access delays, understand its impacts, and explore new opportunities. We hope this study can lead to a better understanding of memory system performance and stimulate new ideas and methodologies to address the memory-wall problem.

The memory-bounded model is first introduced for parallel computing, where more than one computing element works together to solve one common problem. Today, parallel computing is prevalent. Even cell phones have been equipped with multi-core processors for better performance. Parallel processing is a must-know for anyone interested in computer systems. In this paper, we first review the three laws for parallel processing, i.e., the Amdahl’s Law^[4], the Gus tafson’s Law^[5], and the Sun-Ni’s Law^{[2, 3]}, and then discuss and investigate the impacts of the Sun-Ni’s Law ¹. The Amdahl’s Law presents a limitation of parallel processing. The Gustafson’s Law introduces the concept of scalable computing. The Sun-Ni’s Law states that memory is a constraint of parallel computing. Revisiting the memory-bounded speedup model and understanding its full potential will benefit computing in general in the big data era.

The rest of this paper is organized as follows. In Section 2, we introduce the background knowledge of parallel computing, the Amdahl’s Law, and the scalable computing concept. Section 3 introduces the memory-bounded speedup model and its relationship with the fixed-size and fixed-time speedup model. The study on memory system performance, optimization, and redesign and rethinking are given in Sections 4, 5, and 6, respectively. Finally, we conclude the paper in Section 7.

2.   The Amdahl’s Law and ScalableComputing

Parallel processing is for performance gain. Performance evaluation is essential for parallel processing. Speedup is the most used performance metric for parallel processing, which is defined as sequential execution time over the parallel execution time of the program. Let $T_{i}$ be the time required to complete the workload in parallel on i processors, where $T_{1}$ is the execution time on one processor. The speedup of a parallel program with p identical processors is defined as:

Parallel processing has overhead, or degradations, in a more formal term. There are four main degradations of parallel processing. They are uneven workload distribution (load imbalance), communication delays, synchronization costs, and extra computation. These degradations are applications dependent. They could vary largely from application to application and from computer system to computer system. It is very important to understand and optimize parallel processing for better performance.

2.1   The Amdahl’s Law

Gene Amdahl is one of the most famous computer architects in computing history^[4]. He was the architect of the IBM mainframe, the dominant computer in the 1960s and 1970s. His architectural design principle, also known as the Amdahl’s Law, which can be summarized as follows^[4]: ``The execution time of any code always has two portions; portion 1 is not affected by architecture enhancement, and portion 2 is affected by the enhancement. Then, based on this assumption, after the architecture enhancement, portion 1 will be unchanged, and portion 2 will be improved''. Therefore,

Since the execution time of portion 1 will not be reduced, after the enhancement, it may become the performance bottleneck, and enhancing portion 2 further may not help the overall performance. The Amdahl’s Law of the architectural design is a law that calls for a balanced architectural design.

Applying the above Amdahl’s Law to parallel processing, and assuming that portion 1 is the sequential processing portion that cannot be parallelized, and portion 2 is the parallel processing portion that can be perfectly parallelized, we get the Amdahl’s Law for parallel processing:

where a is the percent of sequential execution workload which cannot be parallelized and p is the number of processors for parallel processing. Recall that the new is parallel processing time and the old is sequential processing time, we get:

Substituting it into (1), we get:

(2) is known as the Amdahl’s Law (for parallel processing)^[4]. The Amdahl’s Law shows that the speedup of (2) has an upper bound of 1/a. Assuming that the sequential fraction is 10%, a very reasonable number, no matter how many processors are used, the upper bound of speedup is $10$. The speedup of $10$ is under the assumption that there is no other parallel processing overhead except the sequential execution part. In practice, with the consideration of parallel processing overhead, the actual speedup will be even less. The Amdahl’s Law gives a pessimistic upper bound of parallel processing. Due to the influence of the Amdahl’s Law, for a long time, all the supercomputers only have no more than eight computing nodes^[6].

2.2   Scalable Computing and the Fixed-Time Speedup

The pessimistic view toward parallel computing was changed when John Gustafson and his colleagues published their bombshell results in 1988 in the SIAM Journal on Scientific and Statistical Computing, in which they achieved more than one thousand speedups on three different scientific applications^[5]. These results are real but in conflict with the Amdahl’s Law. Their experiments are conduced under a different assumption of the Amdahl’s Law, which leads to the concept of scalable computing. The argument of Gustafson is that when we have more computing power, it may not be necessary for us to solve a given problem faster; instead, we may like to solve a larger problem which otherwise cannot be solved in a given time. For instance, for weather forecasts, if we have a more powerful machine, we may not want to give the forecast early at 5 p.m. but like to add more parameters and more computations into the weather simulation for a more accurate solution within the same time. This argument applies to any real-time applications, such as missile control or tsunami warning systems. The argument that the problem size should increase with computing power for many applications leads to the concept of scalable computing. Since Gustafson used fixed execution time to constrain the problem size scaling^[5], he introduced the fixed-time speedup model.

The fixed-time speedup model argues that the size of the problem should scale up with the increase in computing power within a given time^[5]. Let W be the amount of original work, and $W'$ be the total amount of scaled work. The fixed-time speedup $S_{\rm FT}(W')$ is defined as:

Assume that the time used for sequential processing of original workload W is the same as the time required for parallel processing of scaled workload $W'$ with p processors. The condition $T_1(W)= T_p(W')$ must be satisfied. Hence, (3) becomes:

Following the Amdahl’s Law, we assume the original workload W only consists of two parts, a sequential part $W_1$ and a perfectly parallel part $W_p$. Recall that a is the sequential portion of the original workload and ($1-a$) is the parallel portion of the original workload. Let us also assume that the scale of the workload is on the parallel processing part only, i.e., $W_1' = W_1 = a \times W$. If there are p processors available then they can do p times more work than a single processor could do. Therefore, the parallel work of scaled workload is: $W_p' = p \times W_p = ( 1 - a ) \times p \times W$. Without considering any overhead, the fixed-time speedup $S_{\rm FT}(W')$ becomes:

(4) is known as Gustafson’s scaled speedup^[5]. Based on (4), the fixed-time speedup will increase with the number of processors without any inherent theoretical upper bound. This simple formula is very powerful. It shows the potential of parallel computing. It got the attention of Wall Street. Wall Street Journal reported Gustafson’s work and recognized that the future of parallel computing is bright. All stocks in the parallel computing industry were boosted. The scalable computing concept has changed the history of parallel computing and computing in general.

In the Amdahl’s Law, an execution workload does not change with the improvement of computing power. Therefore, after the fixed-time speedup is introduced, it is also known as fixed-size speedup. Many people call fixed-size speedup Strong Scaling since it only scales up the number of processors but not the problem size, and call any scalable computing Weak Scaling. In fact, the Amdahl’s Law shows Strong Scaling does not scale if it has a sequential processing portion, and the Gustafson’s Law shows Weak Scaling can scale up with no limitation under the speedup measurement.

3.   Memory-Bounded Speedup: The Sun-Ni’s Law

While (4) successfully puts the end of the Amdahl’s Law for scalable computing applications, as the Amdahl’s Law, it does not consider the parallel processing overheads. Therefore, how to achieve a good speedup in engineering practice is still a dilemma facing the high-performance computing (HPC) communities. However, this time we call for the development of engineering solutions to address these overheads instead of hopelessly facing an inherent unsolvable performance upper bound. In addition to these overheads, researchers quickly noticed another constraint for scalable computing, the memory capacity^{[2, 3, 7]}. When the problem size is larger than the memory system can support, the performance will become extremely low, and there will be no parallel processing gain.

In practice, memory is a costly resource and often limits the increase of problem size. The memory-bounded speedup model, also known as the Sun-Ni’s Law^{[2, 3]}, is introduced, which considers memory as the constraint of scalable computing rather than execution time. Like the fixed-time speedup, the memory-bounded speedup scales up the problem size. The difference is that in memory-bounded speedup, memory capacity, rather than execution time, is the constraint of the problem size scaling. In memory-bounded speedup, the scaled problem size (workload) that can be solved within a parallel computing system is limited by the amount of memory available on the system.

3.1   The Memory-Bounded Speedup

Let $W^{*}$ be the total amount of scaled workload under a memory capacity constraint. The memory-bounded speedup $S_{\rm MB}(W^{*})$ is defined as:

Let g be a function to denote the relationship between memory requirement and workload. We have:

and

where W and M are the workload and the memory capacity of a single processor, respectively.

Assuming that the number of processors and their associated memory are increased in pair, with p processors, the total available memory capacity becomes pM. Therefore, under the memory-bounded constraint, the scaled workload $W^{*}$ is determined by:

Following the same assumption as the Amdahl’s Law and the Gustafson’s Law, we assume $W^{*}$ only contains two parts, a sequential part $W_1^{*}$ and a perfectly parallel part $W_p^{*}$. Recall that a is the sequential portion of the workload and ($1-a$) is the parallel portion of the workload. We assume the scale of the workload is in the parallel part only, i.e., $W_1 = W_1^{*}$ = $a \times W$. With a similar reduction as the fixed-time speedup, we get the memory-bounded speedup:

Now, the question is how we find the memory-scaling function g. In general, finding the function g is application-dependent and is a state-of-the-art. Interested readers can read Section 5 for memory-bound analysis methods and tools. However, since in practice most algorithms are with polynomial time complexities, the memory-scaling function g between M and $W^{*}$ often is a polynomial function or approximated as a polynomial function. For scale-up analysis, we only need to consider the most significant term of the polynomial expression. That is, we can consider g as a power function $g(x)=c \times x^{b}$, where c is a real constant and b is a ration number. And $\bar{g}$ is a pair function of g with coefficient of 1, $\bar{g}(x)=x^{b}$. We have $g(pM)$ = $c \times (pM)^b$ = $p^{b}\times c \times M^{b}$ = $p^{b} \times g(M)$ = $\bar{g}(p) \times g(M)$. Therefore, (5) can be simplified as:

We use matrix multiplication as an example to illustrate how to calculate the memory-bounded speedup. In dense matrix multiplication, the multiplication needs $2k^3$ computation and $3k^2$ memory, where k is the dimension of the two $k\times k$ source matrices. Therefore,

and

Following (6), the memory-bounded speedup for matrix multiplication is:

For a = $0.1$ and p = $16$, the memory-bounded speedup is:

Recall that the perfect speedup is $16$ with $16$ processors. Dense matrix-matrix multiply can achieve a very high speedup based on memory-bounded speedup.

The memory-bounded speedup has linked the fixed-time and fixed-size speedup together. When $g(pM) = W$, the memory-bounded speedup model resolves to the Amdahl’s Law with a fixed problem size. If $g(p M) = pW$, then the memory-bounded speedup model is identical to the Gustafson’s Law with a fixed execution time. In general, computational workload grows faster than the memory requirement; thus $g(pM) > pW$, and the memory-bounded speedup model offers a higher speedup than fixed-size and fixed-time speedup. Since $g(pM) > pW$ in general, the impact of the sequential portion may decrease under the memory-bounded speedup, indicating that a higher speedup would be possible with a larger system.

The memory-bounded speedup has become more and more popular due to two reasons. First, the memory-bounded model sparked the memory-wall problem, and the memory-wall problem fused the importance of the memory-bound (see Subsection 4.1). Second, the memory scale-up is easy to use and easier to get better performance, and memory performance is an important performance concern in engineering practice.

3.2   Memory and Computing Trade-Off

The memory-bounded speedup model is the first model to reveal that memory is a performance constraint of computing. Function $W=g(M)$ provides a quantifiable mathematical formulation for the trade-off between memory and computing requirement. In fact, the memory-scaling function g(M) reflects not only the memory requirement but also the data reuse rate of the underlying algorithm ².

From the algorithm design perspective, due to the memory-wall problem, we need to reduce the memory requirement and increase the data reuse rate. These two goals often conflict with each other and need to be balanced. The function g unifies these two concerns together and provides a unified way for balanced design optimization.

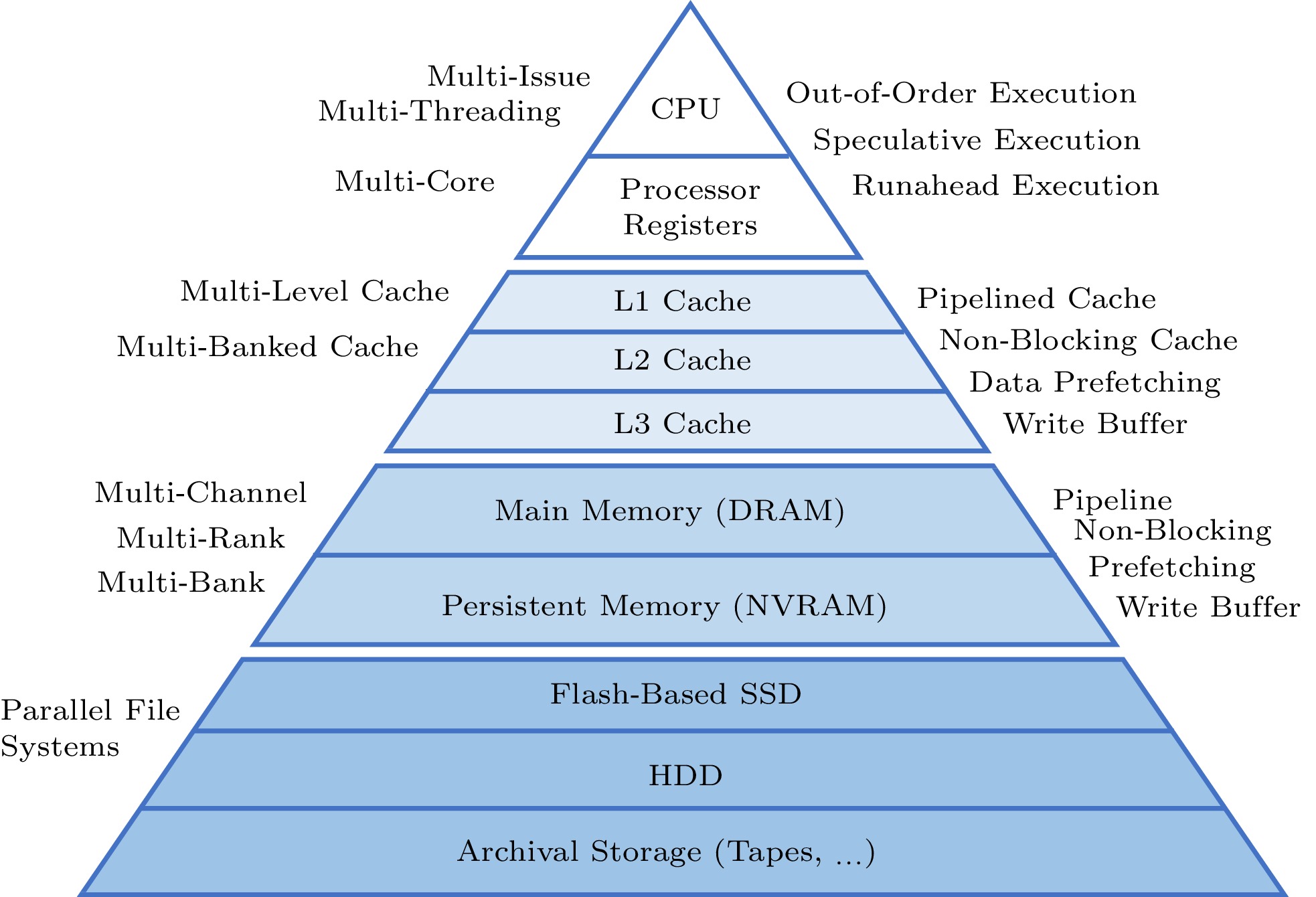
From the architectural perspective, M is the memory requirement, and W is the corresponding computation requirement. Faster computation requires faster memory; otherwise, its computing power will be wasted while waiting for data. This is transferred into how much architecture effort/resource should be used for computing and how much should be for memory. For computer micro-architecture, an immediate design decision is how much the die area should be used for computing and how much should be used for cache^[8]. Cache technology is widely used to mitigate the speed gap between the processor and the main memory. Before 1989 there was no Intel processor with on-chip cache ³. By 2010, as shown in Fig.1, more than 80% of the die area of a chip is used for caching and data, based on [9].

Figure  1.  Silicon area distribution of modern chips.

下载: 全尺寸图片 幻灯片

4.   Performance Fundamental

The memory-bounded speedup model was introduced in 1990^{[2, 3]}. Over the years, it has made impacts in different aspects of computing, far beyond scalable computing. In this section, we highlight some of its impacts on the performance evaluation of memory systems and scalable computing. In the next two sections, we will discuss its impacts on memory system optimization and data-centric rethinking, respectively.

4.1   The Relation Between Memory-Bound and Memory-Wall

Since sequential computing is a special case of parallel computing with $p = 1$, the concept of memory bound can be extended to sequential computing as well. Four years after the memory-bounded concept was introduced, and the memory-wall problem was formally introduced in 1994^[1]. It notices that the performance gap between CPU and memory becomes larger and larger and, therefore, CPU performance is bounded by memory performance and the bound is worsening every year. It calls for effort and solutions to improve memory system performance ⁴.

In order to bridge the performance gap between processor and memory, memory hierarchy with cache is introduced to hide the long delay of off-chip main memory accesses. The smaller, faster, and more expensive cache is closer to the processor. This design aims to provide a memory system that, in ideal, costs almost as the memory devices and the performance is almost as the cache. Memory hierarchy mitigates the memory-wall effect. But, could a memory hierarchy solve the memory-wall problem and memory-bound constraint, not just mitigates it? To answer this question, let us first ask: can we build a large memory system to solve the memory-bound constraint? The answer is no. Based on the memory-wall problem, the gap between computing and memory becomes larger and larger, and we cannot be bounded by the memory performance. Otherwise, can we build a large cache to remove the memory-bound constraint? The answer is also no. Cache has to be fast enough to match the performance of CPU. It needs to find the data quickly, hopefully in the first shot, and has no time to calculate the location of the data. In practice, that means it must be small in size. Since L1 must be small, we need multiple levels of cache to match the difference when the gap between CPU and memory is large. Memory-bound says computing performance is bounded by the memory performance and capacity. The memory-wall problem says the performance gap between CPU and memory becomes larger and larger. Memory hierarchy mitigates the memory-wall problem but makes performance optimization more complex. During the years, theoretical results have been proposed for layered performance matching^[11], and software tools has been developed to measure memory-bound automatically^[12].

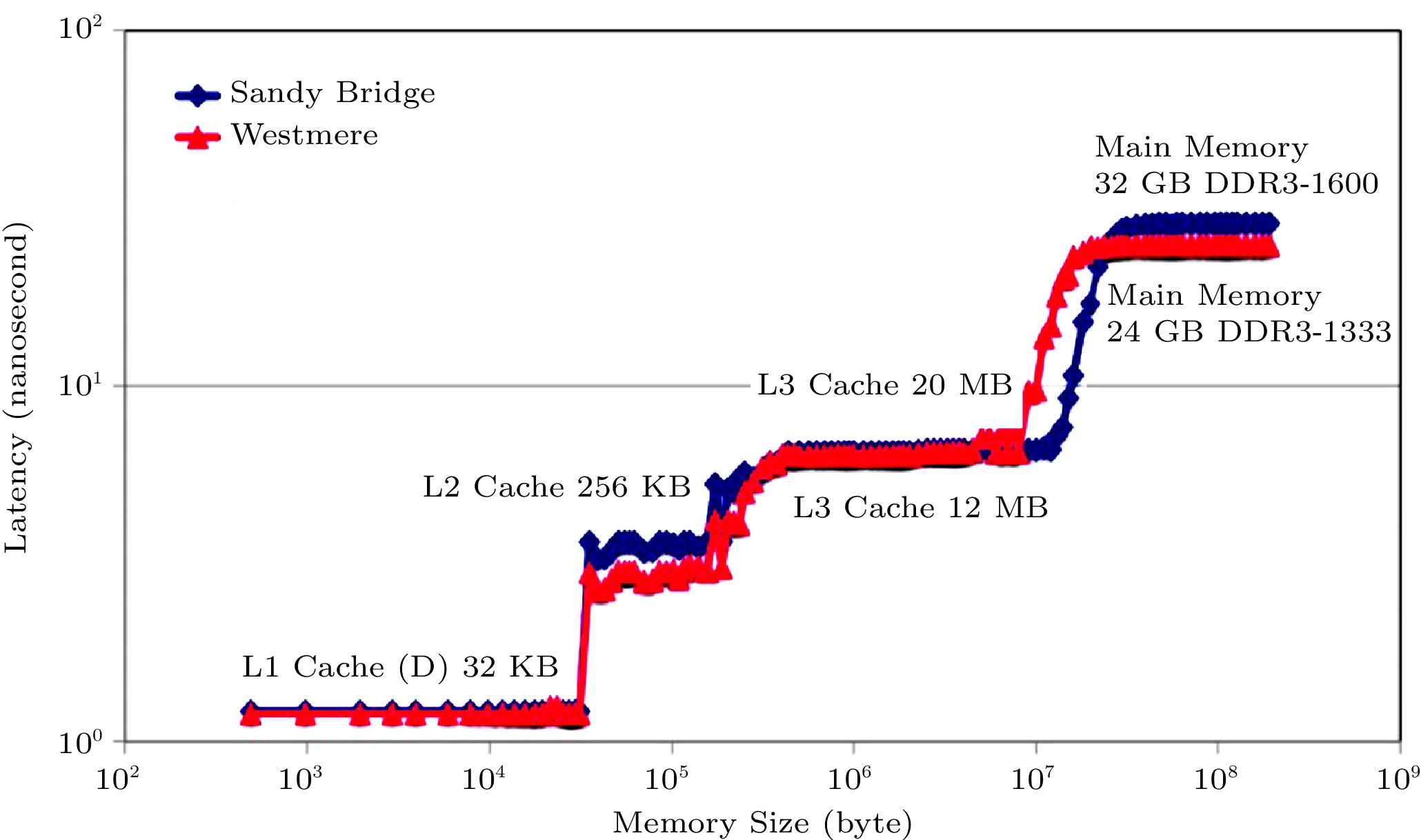
Fig.2^[13] shows the memory latency of the Intel Xeon E5-2670 (Sandy Bridge) and Intel Xeon X5670 (Westmere). With the introduction of the memory hierarchy, the memory latency function shows a four-step ladder pattern. Each step corresponds to the L1 cache, L2 cache, L3 cache, and main memory, respectively. The larger level is further away from the process and has greater access latency. It shows that the memory-bound constraint and memory-wall problem is a global memory system performance issue, which is more complicated to be understood and optimized in a hierarchical memory system.

Figure  2.  Memory latency variation of Westmere and Sandy Bridge^[13].

下载: 全尺寸图片 幻灯片

4.2   The Generalized Speedup

Based on the memory-bounded model, large parallel computers have larger memories, and single-processor computers have smaller memories. How to run a scaled workload $W^{*}$ on a single processor is a problem in practice. This leads us to rethink the definition of speedup.

The traditional definition of speedup is the ratio of sequential execution time to parallel execution time^[2-5]. However, speedup should be the speed up of parallel processing. That is parallel speed over sequential speedup. The traditional definition is correct under the traditional assumption that the problem size is fixed. With a fixed problem size, time reduction is the same as speed up. With this understanding, Sun and Gustafson^[14] introduced a new definition of speedup, the generalized speedup:

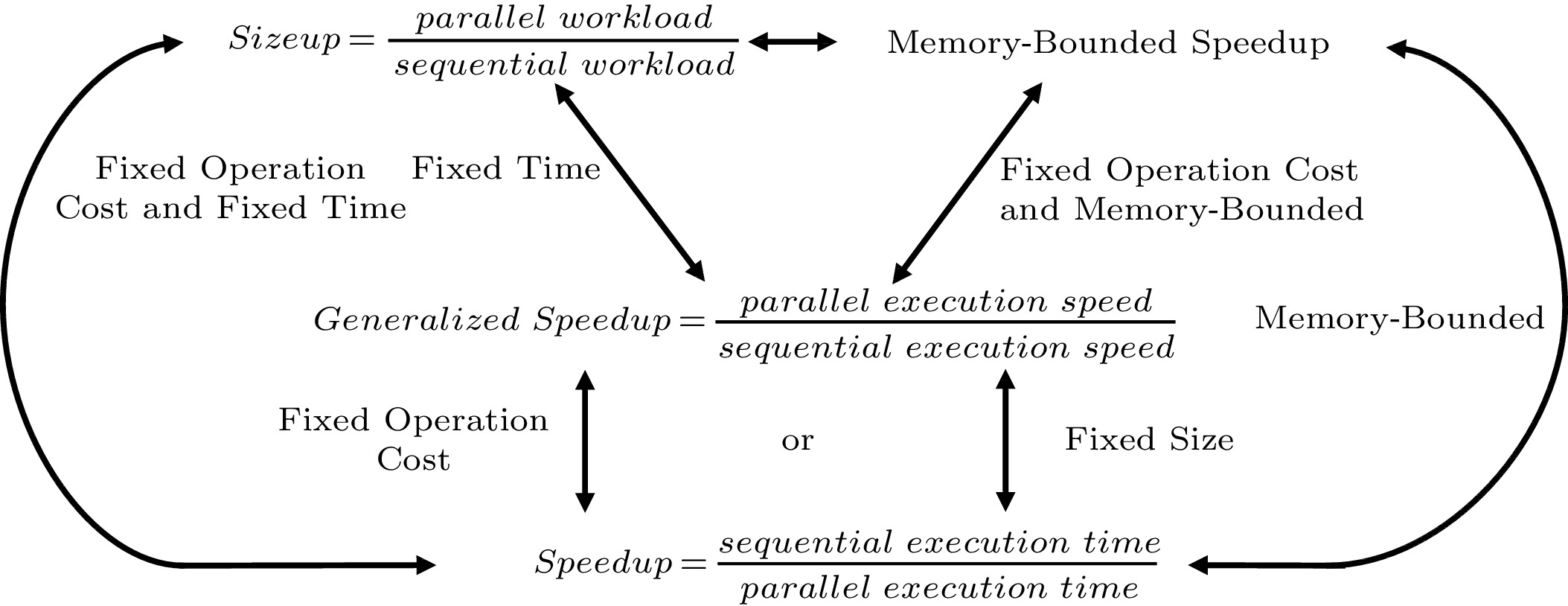
where speed is defined as the amount of work divided by the execution time. The key point of generalized speedup is that the parallel speed is the speed of solving a scaled-up problem size under the time constraint or memory constraint, and the sequential single node speed is the speed of solving the original work size. Therefore, the memory constraint will not influence the sequential computing performance ⁵.

When the execution time is fixed, the generalized speedup becomes work increases, as shown in Fig.3. Therefore, the fixed-time speedup is also called sizeup. When the operation cost is fixed for all kinds of work or when the problem size is fixed, the generalized speedup is the same as the traditional speedup. Fig.3 summarizes the relationship between the generalized speedup, sizeup, traditional speedup, and memory-bounded speedup^[14].

Figure  3.  Generalized speedup and its relations with speedup models.

下载: 全尺寸图片 幻灯片

4.3   Scalability

Scalability is the ability to maintain parallel processing gain when both the problem size and the system size increase. Parallel efficiency is defined as parallel speedup divided by p, where p is the number of parallel processors used for parallel processing^[15]. The definition of parallel efficiency is straightforward since p is the ideal and perfect parallel performance gain with p processors. A natural way to measure scalability is to measure the ability to maintain parallel efficiency. Kumar et al.^{[15, 16]} introduced the concept of isoefficiency. Isoefficiency measures how much work must be increased on a larger machine in order for the efficiency to remain constant.

Isoefficiency is a correct approach. However, its underlying speedup is still the traditional speedup and may have the memory-bounded issue. In practice, measuring the sequential execution time of large applications on a single node is either impossible due to memory limitation or very slow if virtual memory is supported. For scalable computing, the speedup should use the generalized speedup, and the isoefficiency should be the isoefficiency of the generalized speedup^[17]. Maintaining the efficiency of the generalized speedup, in the meantime, is equal to maintaining the average speed per computing node. With the above observation of the generalized speedup, Sun and Rover^[18] proposed isospeed as a measurement of scalability. Based on [18], an algorithm-machine combination is scalable if its achieved average unit speed can remain constant with the increasing number of processors, provided the problem size is increased proportionally. The average unit speed is the achieved speed divided by the number of processors. By definition, the scalability function from system size p to system size $p'$ can be defined as:

where W is the initial workload executed when p processors are employed, and $W'$ is the scaled workload executed when $p'$ ($p' > p$) processors are employed to maintain the average unit speed. The workload $W'$ is determined by the isospeed constraint. In the ideal situation, $W' =\frac{p' \times W}{p}$ and $\psi (p,p')=1$. In general, $\frac{W'}{p'}>\frac{W}{p}$ and $\psi (p,p')<1$. An isospeed function closer to 1 implies that the parallel system is highly scalable.

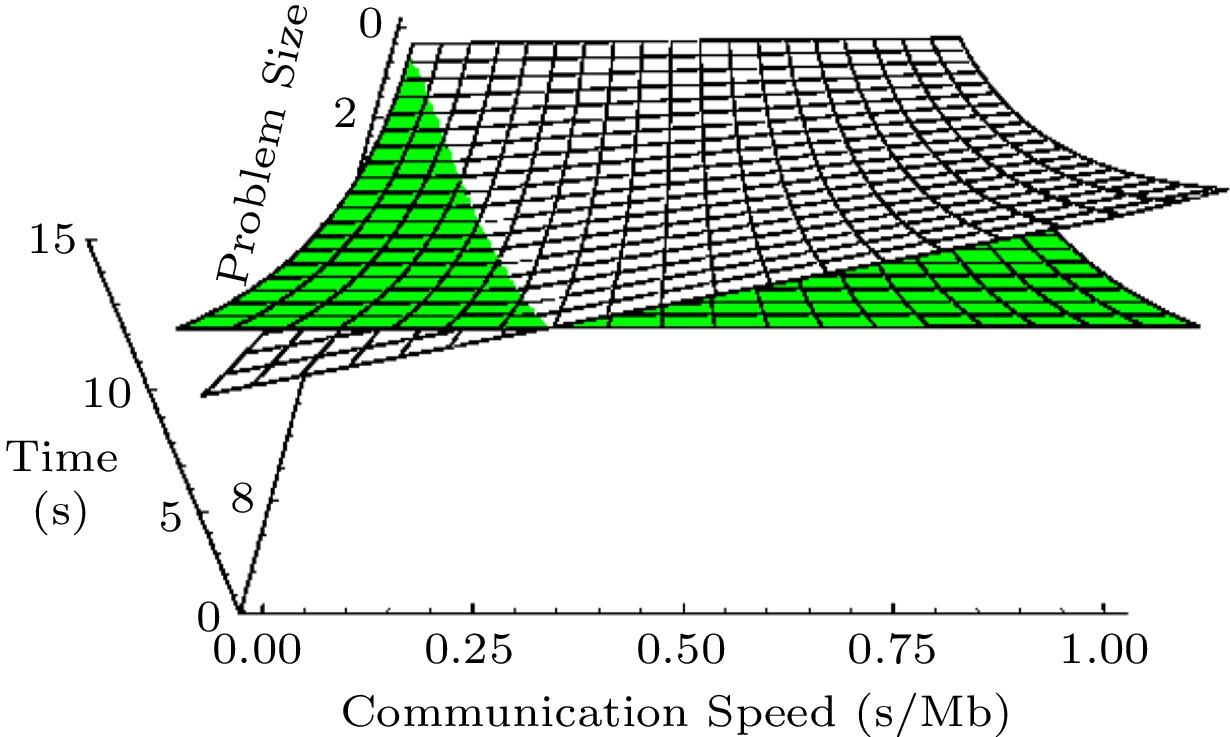
Scalability has many applications. One application is to find the best range of an algorithm and to find the performance crossing point of two different algorithms^{[19, 20]}. Range comparison compares the performance of programs over a range of ensembles and problem sizes based on scalability and crossing-point analysis. It plays a crucial role in scalable computing. Fig.4 demonstrates a performance range comparison of the PDD (Paralled Diagonal Dominant) and parallelized Thomas algorithm when the communication speed varies^[20]. From Fig.4, we can see that crossing points exist and vary with data access/communication bandwidth.

Figure  4.  Performance crossing due to scalability^[20].

下载: 全尺寸图片 幻灯片

4.4   Scalable Computing for Multi-Core Architecture

Parallel processing can be carried out at different levels. In order to overcome the limitations, including the power consumption limitations, of uni-core architectures, multi-core architectures have been developed. Multi-core architectures integrate multiple processing units (cores) onto one chip, thereby increasing the computing capacity via parallel processing while consuming less power. As microprocessor architectures enter the multi-core era, the scalability issue is also carried into the multi-core architecture design.

At the 40 years of the Amdahl’s Law, Hill and Marty^[21] analyzed multi-core scalability under the Amdahl’s Law and pessimistically argued that the future of scalable multi-core processors is dim. Sun et al.^{[7, 22]} analyzed multi-core scalability under fixed-time and memory-bounded conditions. Assuming the multi-core systems under study are symmetric, and task W has two portions: data processing work, $W_p$, and data access (movement) work, $W_c$. Based on the Gustafson’s Law, the fixed-time speedup for multi-core architectures is:

where $W_p' = p \times W_p$ and $f^{'}$ is defined as:

(7) shows if $W_{c}$ remains unchanged when the core number and workload increase, then the multi-core fixed-time speedup can increase linearly. The memory-bounded speedup model for multi-core architectures is also introduced in [7, 22], which has a better speedup than that of fixed-time speedup. Multi-core is scalable for scalable computing.

Please notice that here the claim of multi-core is scalable is under the assumption that data access delay is unchanged when the core number and the problem size increase. This assumption is not a theoretical bound but is hard to achieve in engineering practice. In other words, multi-core is memory-constrained. Multi-core architectures have put more pressure on the already lag-behind memory systems.

5.   Performance Optimization

In this section, we discuss the impacts of the memory bound principle from the angles of algorithm design, performance tool development, memory data access optimization, and I/O data access optimization, respectively, in each subsection.

5.1   Memory-Bounded Algorithms and Analysis

Over the years, more and more researchers in the computing community have accepted the memory-bounded concept and applied it in their study. A new branch of algorithm analysis, called memory-bound functions, was developed in the 2000s^{[23, 24]}. In formal (sequential) algorithm analysis, the challenge of the memory-bounded analysis is no longer the scalability, but the applications with unpredictable data requirements. The argument is that if we know the memory need, we can provide an appropriate memory (in theory). The difficulty is that we do not know the need. Therefore, the theoretical arithmetic memory analysis is focused on a memory-bound function whose execution time could be dominated by memory accesses since they have unpredictable data requirements. The (general) memory-bound functions have been proven to be very effective in preventing the proliferation of junk email by introducing an artificial cost in the form of expensive memory accesses^{[23, 24]}. By using memory-bound functions, the email sender is asked to pay the cost of the memory access latency imposed by the memory-bound functions before the email is sent.

In addition to the new branch of theoretical “complexity” analysis of unpredictable memory requirements, the memory-bounded and memory-constraint analysis have been widely used in algorithm designs for predictable memory requirements as well, in areas such as graph search, dynamic programming, and distributed optimization, to list a few.

The A* algorithm^[25] is a commonly-used path search and graph traversal algorithm. One major practical drawback is that it requires an explosion of memory usage and a long execution time, as it stores all generated nodes in memory. Several algorith-ms^[26-29] are proposed to improve the A* algorithm for this purpose. Among them, the IDA* algorithm^{[26, 27]} combines the ideas of the A* algorithm and the iterative deepening depth-first search algorithm. The key feature of the IDA* algorithm is that it does not keep track of every visited node, which saves significantly on memory consumption. At each iteration, IDA* performs a depth-first search, cutting off a branch if its total cost exceeds a given threshold. A threshold is set as the estimate of the cost of the initial state. If no solution is found, the threshold is increased, and the search is repeated until a solution is found. At each iteration, the threshold used for the next iteration is the minimum cost of all values exceeded the current threshold. IDA* has a better memory usage than A*. More specifically, IDA* has a polynomial space complexity, O(bd), where b is the maximum branching factor and d is the maximum depth of the tree. Whereas the space complexity of A* is exponential and is $O(b^{d})$.

Researchers in artificial intelligence and operations research have been studying decision making under uncertainty. Seuken and Zilberstein introduced the Memory-Bounded Dynamic Programming (MBDP) algorithm^[30] to identify a small set of policies that are actually useful for optimal or near-optimal behavior and to avoid keeping too many policies in memory. Furthermore, an improved version of MBDP^[31] is proposed to improve the scalability of MBDP further by reducing the complexity with respect to the number of observations.

With the development of big data and artificial intelligence, distributed optimization has become essential for solving large-scale problems. In order to reduce the memory requirements, a number of distributed optimization algorithms^[32-36] have been proposed that seek a trade-off between the quality of the solutions and the memory consumption. Among them, MB-DPOP^[36] iteratively performs memory-bounded utility propagation to use a customizable amount of memory and to guarantee performance.

Memory-bounded analysis and memory-bounded principle have been widely embedded into algorithm design today. We have just discussed a few representing examples here.

5.2   Performance Analysis Tools

Memory-bounded analysis tools are important for practitioners, especially for software developers who do not have the knowledge or expertise to analyze the underlying algorithms of a given software system. In many situations, software performance tools play an important role in optimization.

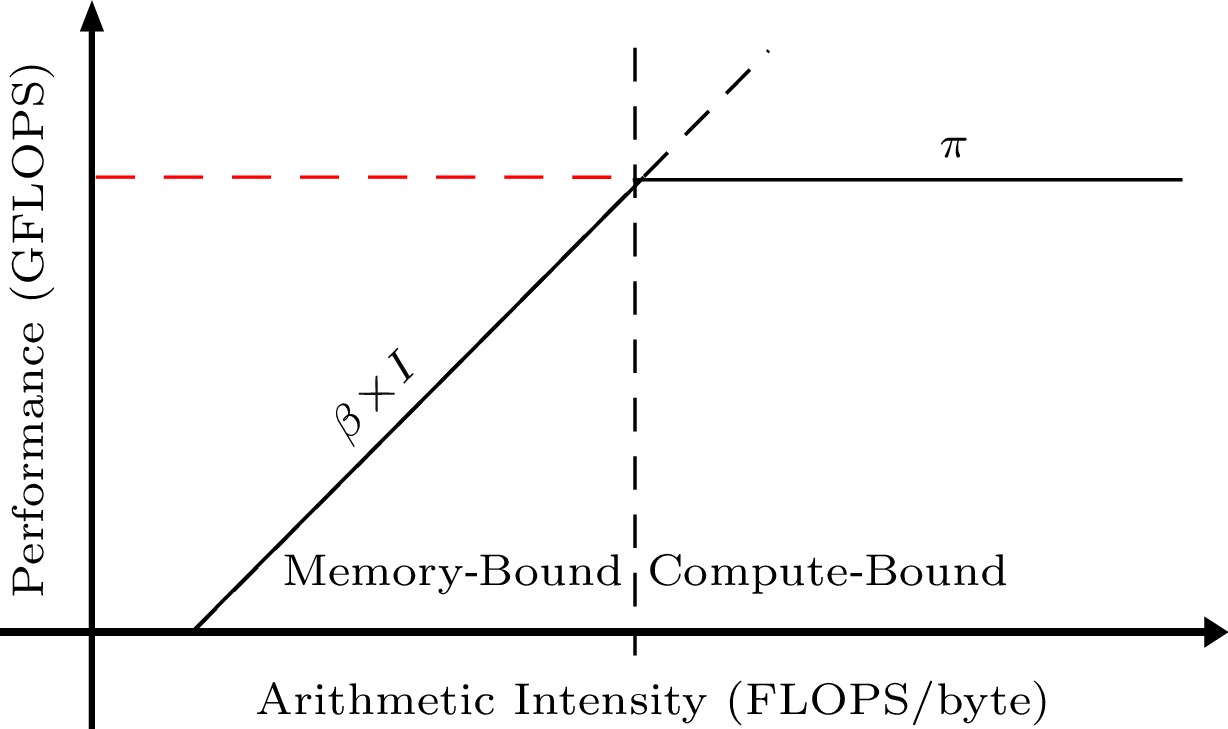
The Roofline model^{[37, 38]} is a performance analysis model to calculate the performance bound for a given computation on a specific target architecture. The standard Roofline model (as illustrated in Fig.5) considers machine peak performance $\pi$, machine peak bandwidth $\beta$, and arithmetic intensity I of the application to analyze the performance bound in GFLOPS.

Figure  5.  An example of the standard Roofline model^{[37, 38]}.

下载: 全尺寸图片 幻灯片

However, estimating the machine characteristics required by Roofline analysis is time-consuming and difficult. Even if machine characteristics can be estimated, these are theoretical maximums that do not necessarily reflect the actual software system performance. In order to solve this problem, the Empirical Roofline Tool (ERT)^[12] is developed to determine architecture characteristics and application kernels to populate the Roofline model automatically. With the help of ERT, software developers can measure performance bound in practice, which provides them with guidance on optimizing their code for maximum performance, such as what types of parallelism are required and what compiler(s) to use.

5.3   Modeling and Optimization of Memory Systems

As pointed out in Subsection 4.1, the memory hierarchy is adopted in modern computer systems to mitigate the memory wall problem. In addition to memory hierarchy, techniques that utilize data concurrency and memory parallelism are also widely used in modern processors and memory systems to reduce memory access latency^[39-41]. A large amount of data concurrency exists in each layer of the memory hierarchy^[42-45]. For better using this concurrency, data access concurrency needs to be considered in memory system modeling and optimization to utilize the existing memory concurrency.

C-AMAT (Concurrent-AMAT)^[44] is a memory access performance model that extends AMAT (average memory access time)^[10] to quantitatively measure the combined impact of memory access locality and concurrency with the consideration of all data access overlapping. C-AMAT is defined as the average memory access time with the consideration of concurrent hit and miss accesses. It can be calculated as the number of memory active cycles divided by the number of memory accesses:

where $\omega$ represents the total number of cycles executed in which there is at least one outstanding memory reference, and $\alpha$ represents the total number of memory accesses.

Similar to AMAT, the C-AMAT model can be calculated at each level of the memory hierarchy and is recursive^[41]. The C-AMAT model provides a new perspective for cache optimization: data access concurrency is as important as data locality. The principle of optimizing a memory system is not locality, locality, and locality, as some articles promoted. It is a balanced design of data locality and concurrency. C-AMAT has already found its applications in traditional system optimizations, such as data replacement^{[40, 46]} and prefetching schemes^[39], and in new architecture designs, such as PIM^[47] and GPU^[48].

Memory hierarchy systems call for global performance analysis and global performance optimization of the overall performance of a memory hierarchy system. Based on C-AMAT, an optimization method named LPM (layered performance matching) is presented in [11]. The rationale of LPM is to reduce the overall data access latency through the matching of the data request rate and the data supply rate at each layer of a memory hierarchy, with a balanced consideration of data locality, data concurrency, and overlapping of data accesses. Let LPMR(l) be the layered performance matching ratio at memory level l. Let $\lambda$(l) be the request rate from the upper layer $l_{i-1}$, and let $\nu$(l) be the supply rate at level l. The layered performance matching ratio is the ratio of the request rate and the supply rate between any two memory layers:

Fig.6 shows a memory hierarchy with a three-level cache and main memory. Each level receives access requests from the upper level and responds with its own data or the data grabbed from the lower level.

Figure  6.  The layered performance matching.

下载: 全尺寸图片 幻灯片

Based on the data access delay tolerance of the user, LPM can calculate the required matching ratio at each layer of the underlying memory hierarchy^[11]. LPM transfers the global performance optimization problem of a memory hierarchy to several relatively simple local optimizations at different layers of the memory hierarchy. It has real potential to reduce data access delay, as shown in the next subsection.

5.4   Deep Memory and Storage Hierarchy

To address the memory-wall problem, the memory system has been undergoing extensive changes, adopting new technologies and adding more layers to the memory hierarchy, as shown in Fig.7. With the adoption of new technologies, such as NVRAM (non-volatile random access memory) and SSD, and adding new layers between memory and storage, the boundary of memory and storage becomes blurry. Storage becomes a part of the memory system to handle the ever enlarged applications. This leads to the term: Deep Memory and Storage Hierarchy (DMSH)^{[49, 50]}.

Figure  7.  Deep memory and storage hierarchy.

下载: 全尺寸图片 幻灯片

Storage devices are hundreds and thousands of times slower than memory devices, making them the weakest point of DMSH^[51-53]. The good news is that the LPM methodology has bundled it into the global DMSH performance. On the other hand, because storage devices are so slow, we can develop software solutions to improve their performance. The LPM methodology has linked the storage performance with the global DMSH performance^[11]. Based on the LPM principle, a new, heterogeneous-aware, multi-tiered, dynamic, and distributed I/O buffering system, named Hermes^{[53, 54]}, is developed. We use the term multi-tiers here, because under Hermes different memory/storage devices can be accessed concurrently in hierarchical or horizontal fashion. Hermes enables, manages, supervises, and, in some sense, extends I/O buffering to integrate into the DMSH fully. Hermes provides novel data placement policies to utilize all memory and storage technologies efficiently. Additionally, Hermes adopts several novel techniques to perform memory, metadata, and communication management in multi-tiered buffering systems. Performance evaluations show Hermes dramatically speeds up I/O, exceeding the performance of state-of-the-art buffering platforms by more than 2x. The first version of Hermes has been released under the HDF5 library by the HDF group as an open source ⁶.

6.   Data-Centric Thinking and Data-Centric Design

Big data applications have increased data velocity, veracity, volume, and variety^[55]. These four V characteristics have put unprecedented pressure on memory and storage systems. Even worse, from a computing point of view, the pressure of big data applications is not only from the four Vs but also from that they have totally changed the way of computing. For example, let us find the best travel path from city A to city B. From the traditional computational thinking, we first find all the roads from A to B, make a graph based on the road-map, and then run the shortest-path algorithm on the road-map to find the shortest path from A to B. From the data-centric thinking, however, the problem will be solved total differently. To find the best path from A to B from a data-centric approach, we first record which path people used most and then use it as the best one. If we use the GoogleMap App, GoogleMap even can provide the estimated travel time of each path based on the recent travels of other GoogleMap users. We can see that in the data-centric solution, there is almost no computing but data gathering and processing. While computational thinking focuses on formulating a problem to make it computationally solvable, data-centric thinking is for gathering and exploiting data to provide insights^[56]. This paradigm changing requires a rethinking of computer architecture and computer systems. Currently, there are no clear solutions for this paradigm challenge, but improving data access and processing ability certainly is part of the major concern.

Intensive research has been conducted to address the four V issues, and many point solutions exist. GPU is a successful solution for graphic applications^[57]. The MapReduce data structure and MapReduce file systems are successful solutions for information retrieval^[58]. AI chips are designed to address the data processing needs of deep learning^[59], and ASIC and FPGA methodologies are used to address different data processing needs of different applica-tions^{[60, 61]}. PIM (Processing in Memory), NDP (Near-memory Data Processing), and ISP (In-Storage Processing) architectures are proposed to process data in memory, near memory, and in storage, respectively, to reduce data access time^[62-64]. From a system point of view, the LPM methodology and the Sluice Gate theory are proposed to reduce the data access delay as small as possible^{[11, 65]}. The list is long and more can be listed, but the above are good enough to conclude our observations. These solutions are useful, but they are designed for given applications and only work under certain conditions and environments. They can mitigate the memory-wall problem but cannot solve it. Memory-bound remains. There is a call to rethink the fundamental computer system design to address the computing paradigm change^[56]. However, after 60 years of rapid development, computer systems have become so complex that any fundamental change in computer architecture or operating system will be a hard task. With a deep memory-storage hierarchy, the I/O system is part of the enlarged memory system. In the following, we introduce a data-centric system design for I/O systems.

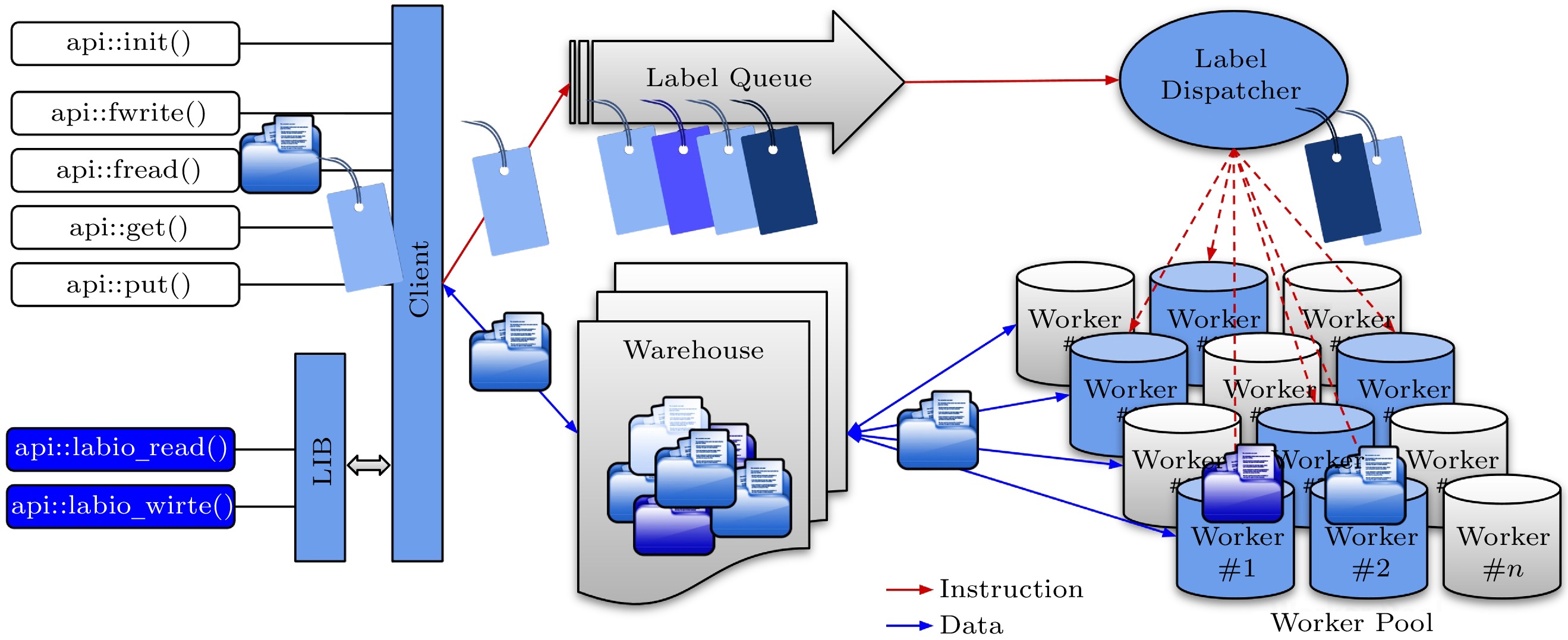
Following the data-centric thinking, a new, distributed, scalable, and adaptive I/O system, LABIOS^[66], is developed to address the divergence in storage architectures and reduce conflicting requirements. In compute-centric systems, a program conducts computing and fetches data when computing needs them. In data-centric systems, computing is with the data and can be carried out where the data is. LABIOS follows the data-centric thinking, where each section of data is labeled, and a label is a tuple of an operation and a pointer to the data. Therefore, the computing is paired with the data and can be carried out where the data is. The idea behind LABIOS is very similar to that behind Amazon warehouses. I/O requests are collected and optimized based on their labels, and the operations are carried out by worker pools at data warehouses. The workflow of LABIOS is shown in Fig.8. LABIOS provides storage flexibility, versatility, and agility due to labels and its decoupled data-centric architecture. With all its merits, putting LABIOS in use requires the update of operating systems and file systems. This will be a long and challenging process. The first operating system study to support the LABIOS system appeared in Nov. 2022 at the SC2022 conference^[67].

Figure  8.  A logical overview of data operation under label.

下载: 全尺寸图片 幻灯片

7.   Conclusions

Professor Kai Hwang is a prominent scholar whose textbooks have influenced several generations of computer scientists and practitioners. In more than one of his books^{[68, 69]}, he has introduced the memory-bounded speedup model and named it the Sun-Ni’s Law. In this study, we reviewed the memory-bounded principle, its history, and its impacts, and discussed its role and potential in the big data era. Prof. Hwang’s textbooks have made a lasting influence, and the memory-bounded model has made its impacts on computing. We think this is the best way to honor Prof. Hwang’s life long achievement and is the best way to make our addition to this special issue.

The memory-bounded speedup model takes into account the effect of memory on performance by relating memory requirement to computational requirement. It reveals the memory constraint in performance, and it sparks the memory-wall problem. The memory-bounded concept has changed how algorithms and software are designed. Moreover, more memory optimization designs and performance models have been developed to mitigate the performance gap between computing and memory systems.

We hope this study will provide a better understanding of the memory-bounded model and its implications, which will help us better understand and gain new insights into memory system performance to promote data-centric thinking and to pave the way for developing next-generation memory systems and optimization tools.