BiGAE: 一种双向生成式自编码器
-
摘要:研究背景
自动编码器 (AEs) 是一种用于高效地编码数据以降低维数,并将编码解码为重构数据的深度学习算法。近年来,随着AEs被广泛应用于图像的分类与重建和异常检测等各个领域,如何提高自编码器的生成和表征能力成为了一个热门的研究课题。由于解码器的生成和编码器的表征是双向的映射过程,因此AEs本质上是一个联合的双向优化问题。近年来,引入并优化基于GAN机制的网络模型逐渐成为AE的重点发展方向。一方面,对于解码的生成能力而言,生成对抗网络(GANs)已经成为最先进的生成模型;另一方面,对于编码的特征表示能力而言,基于GAN的编码器可以有效地从隐变量空间中提取某些分布方向,这些成分对应于数据分布的某些特定语义属性。然而,如何在保证模型收敛的同时,实现编码器和解码器/生成器之间的双向映射的联合优化仍然是一个亟需解决的挑战。实际上,大多数现有的自动编码器不能自动权衡双向映射。这是因为大多数的先前工作都具有以下两个限制之一:1) 许多先前的编码设计依次实现解码/生成过程和编码过程的双向优化,这种耦合训练机制不能保证生成器的生成和编码器的表示同时单独优化;2) 在一些双向训练的网络中,不能单独保证数据空间和隐变量空间的循环一致性,这限制了特征学习的进一步优化。
目的针对研究背景中提出的两个挑战,我们的研究目标是:1)实现自编码器中双向映射的同步优化和联合优化;2)保证编码器和解码器的特征表示能力和数据生成能力分别进行独自优化。此外,在实现上述两个目标的同时,我们还试图保证双向自编码器的收敛性。
方法我们提出了一种基于BiGAN的无监督双向生成式自编码器Bi-GAE。首先,Bi-GAE采用了一个双向学习框架,该框架受到Bi-GAN框架设计的启发,但引入了三个主要的修改,包括在:1)损失函数中引入Wasserstein距离,2)增加一个嵌入式GAN框架来优化真实隐变量空间分布和重构隐变量空间分布的循环一致性,3)为生成器和编码器分别设计两个优化项。一方面,Bi-GAE同时实现了编码器和解码器的双向优化。具体来说,Bi-GAE同时接收编码器和解码器的数据样本和潜在样本的输入,并以有效学习隐变量空间和数据空间的联合分布为优化目标,同时训练它们的表征能力和生成能力。另一方面,引入Bi-GAE的三个主要修改进一步增强了该双向框架的收敛性。其次,Bi-GAE利用添加的两个优化项和嵌入的MMD-GAN结构来优化隐变量/数据空间分布的循环一致性。这些优化提高了Bi-GAE的特征表示能力,同时保留了相比于单向GAN框架而言仍具有竞争力的生成能力。此外,我们从理论上证明了优化真实数据和重构数据/潜在空间分布之间的循环一致性可以提高生成器/编码器特征学习能力的下界。
结果我们进行了大量的实验,从以下三方面来评估Bi-GAE的性能: 1) 编码器的特征表示能力;2)解码器的生成能力;3)AEs整体重建能力。与同类算法相比,Bi-GAE的表征能力使高分辨率图像的平均分类精度提高了8.09%。此外,我们在不同分辨率的多个图像数据集上评估了Bi-GAE的生成能力,发现相比于BiGAN和WGAN,Bi-GAE在生成结果方面具有竞争力。最后,我们发现在512x512重构时,Bi-GAE使SSIM提高了0.045,FID降低了2.48,这反映了整体性能的显著提高。
结论本文提出了一种无监督生成式自编码器Bi-GAE,实现了生成器和编码器的双向联合优化。此外,对于编码器和解码器,我们合理地设计了优化机制来实现真实数据和重构数据/隐变量空间之间的循环一致性优化。在编码过程中,我们嵌入了基于MMD的GAN网络结构来改善特征表示和增强Bi-GAE的收敛性。在解码过程中,我们引入了一个基于SSIM的优化项来引导生成器遵循人类视觉模型。理论分析和实验结果表明,Bi-GAE实现了在具有竞争生成能力的前提下表征能力的提升,并且Bi-GAE在训练中具有稳定的收敛性。
Abstract:Improving the generative and representational capabilities of auto-encoders is a hot research topic. However, it is a challenge to jointly and simultaneously optimize the bidirectional mapping between the encoder and the decoder/generator while ensuing convergence. Most existing auto-encoders cannot automatically trade off bidirectional mapping. In this work, we propose Bi-GAE, an unsupervised bidirectional generative auto-encoder based on bidirectional generative adversarial network (BiGAN). First, we introduce two terms that enhance information expansion in decoding to follow human visual models and to improve semantic-relevant feature representation capability in encoding. Furthermore, we embed a generative adversarial network (GAN) to improve representation while ensuring convergence. The experimental results show that Bi-GAE achieves competitive results in both generation and representation with stable convergence. Compared with its counterparts, the representational power of Bi-GAE improves the classification accuracy of high-resolution images by about 8.09%. In addition, Bi-GAE increases structural similarity index measure (SSIM) by 0.045, and decreases Fréchet inception distance (FID) by 2.48 in the reconstruction of 512×512 images.
-
1. Introduction
Auto-encoders (AEs) are learning algorithms for efficiently encoding data to reduce dimensionality, and decoding the encoding into reconstructed data[1]. Both encoding and decoding processes should have the property of “cycle consistency”[2]. In recent years, AEs have been widely used in various fields such as image classification and reconstruction[3], recommendation systems[4], and anomaly detection[5].
Currently, research on AEs mainly focuses on improving the generative and representational capabilities[1, 6]. Specifically, the generator/decoder (from latent space to data space) focuses on generating data that conforms to the distribution of the real data space, while the encoder (from data space to latent space) aims to extract semantic-relevant feature representations. Since the generation of the decoder and the representation of the encoder are bidirectional mapping processes, the improvement of generative and representational capabilities in AEs is essentially a joint bidirectional optimization problem.
GAN-based networks are a favorable approach to AE. On the one hand, generative adversarial networks (GANs)[7] have emerged as state-of-the-art generative models that enable efficient mapping from simple latent distributions to arbitrarily complex data distributions[8-10]. On the other hand, certain directions in the latent space of GAN-based encoders correspond to specific semantic properties of the data distribution, which can be used to improve representational capabilities[11-13]. For example, Radford et al.[12] showed that a GAN trained on a database of human faces learns to associate specific latent directions with gender and the presence of glasses.
Several previous studies have proposed ways to utilize GANs or adversarial models in AE, such as adversarial auto-encoder (AAE)[14], adversarial latent auto-encoder (ALAE)[15], and bidirectional generative adversarial network (BiGAN)[11]. For example, BiGAN is an unsupervised feature learning framework to bidirectionally train the decoder and the encoder by introducing the GAN's discriminator into the joint space of the data and latent. AAE utilizes the GAN framework when training the encoder, which leads the distribution of encoding results to approximate a Gaussian distribution. Furthermore, ALAE utilizes the style-based GAN (StyleGAN) architecture[8] to train the AE by reconstructing images from the style encoding results of real images.
However, most of these studies[11, 14, 15] have one of the following two limitations. First, a series of AEs with adversarial models sequentially enable the bidirectional optimization in the decoding/generating process and the encoding process. For example, AAE and ALAE usually treat the training process as a coupled optimization. Therefore, they cannot guarantee that the generation of the generator and representation of the encoder are simultaneously and individually optimized in this bidirectional optimization problem. To address this issue, we propose Bi-GAE, an unsupervised bidirectional generative auto-encoder. Specifically, a bidirectional learning framework is proposed based on BiGAN but with three major modifications, namely adopting Wasserstein distance[9], adding an embedded GAN framework on the real and reconstructed latent spaces, and designing two optimization terms for the generator and the encoder, respectively. On the one hand, Bi-GAE realizes the bidirectional optimization of the encoder and the decoder/generator simultaneously. When training Bi-GAE, the encoder and the generator concurrently receive the input of data samples and latent samples to train the representation and generality capability simultaneously with the objective of learning the joint distribution of the latent space and the data space. On the other hand, these three modifications further enhance the convergence of the bidirectional framework.
Second, in some bidirectionally trained networks, the cycle-consistency of the data space and the latent space cannot be guaranteed separately, which limits the further optimization of feature learning. For example, BiGAN enables the bidirectional optimization of the generator and the encoder by distinguishing the joint distribution of the latent space and the data space, but it does not constrain the consistency between the real and reconstructed spaces for the data space and the latent space, respectively. Therefore, it is still a challenge to improve the representational capability of GAN-based AEs with a competitive generative capability, especially for high-dimensional complex data[8, 12, 16]. To address this challenge, Bi-GAE leverages the two added optimization terms and the embedded structure namely GAN based on maximum mean discrepancy (MMD-GAN)[17] to optimize the cycle-consistency of the latent/data space distribution. Meanwhile, we theoretically prove that optimizing the cycle-consistency between the distributions of the real and reconstructed data/latent space improves the lower bound on the feature learning capability of the generator/encoder. Therefore, these optimization schemes enhance the feature representational capability of Bi-GAE, which also retains a competitive generative capability compared with unidirectional GAN frameworks.
We conduct extensive experiments to evaluate the performance of Bi-GAE. Compared with its counterparts, the representational power of Bi-GAE improves the average classification accuracy of high-resolution images by about 8.09%. Furthermore, compared with BiGAN[11] and Wasserstein GAN (WGAN)[18] on multiple image datasets with different resolutions, Bi-GAE achieves competitive results in generation. Bi-GAE increases structural similarity index measure (SSIM) by 0.045, and decreases Fréchet inception distance (FID) by 2.48 in the reconstruction of 512×512 images. In addition, the experimental results also verify that Bi-GAE can achieve stable convergence even for high-resolution images.
The contributions of this paper are summarized as follows
1 .• We propose an unsupervised bidirectional generative auto-encoder framework that introduces two optimization terms on the data and the latent space respectively to improve feature learning with competitive generative capabilities.
• We embed an MMD-GAN structure in Bi-GAE to enhance semantic-relevant feature representation in encoding and alleviate the near-convergence problem of GAN-based AEs.
• We theoretically prove the improvement in the lower bound of the cycle-consistency between the distributions of the data/latent space and the reconstructed data/latent space, enabling further optimization of feature learning for the encoder and the generator in Bi-GAE.
• We introduce the multi-scale SSIM (MS-SSIM) loss instead of the perceptual loss in the cycle-consistency optimization term of the data space, which can mitigate the effect of the unstable gradient vanishing/exploding on the training process. In addition, we theoretically prove that these unstable gradients are caused by the pre-trained weights in the perceptual loss network.
2. Related Work
2.1 GAN Frameworks
GANs are widely used in the field of synthetic image generation[19]. Recently, GANs have made significant progress, especially in the discriminative mechanism and specific optimization of high-resolution image generation[20].
To optimize the discriminative mechanism, some innovative studies focus on the design of the loss function. For example, WGAN[18] introduces the Wasserstein distance with valid gradient as a loss function, while least-squares GAN (LSGAN)[10] introduces the least squares distance as a loss function to enhance convergence. In addition, some studies explore embedding networks in GANs. For example, Johnson et al.[21] used a pre-trained VGGNet model which extracts style features in the image space to compute perceptual loss. Boundary equilibrium GAN (BEGAN)[22] applies an auto-encoder as the discriminator for GANs to improve discriminative sensitivity.
To improve the generation of high-resolution images, many studies focus on optimizing the algorithm or architecture of GANs. For example, Wang et al.[23] designed a multi-scale generator and discriminator by utilizing semantic labels. In addition, other studies design specific training mechanisms for high-resolution images. For example, cycle-consistent GAN (CycleGAN)[2] defines a cycle-consistency loss between the source and the target image space to optimize image-to-image translation with high resolutions. Stacked GAN (StackGAN)[24] introduces a stack of GANs in a multi-resolution pyramid to generate high-resolution images. Progressive growing GAN (ProGAN)[16] proposes a progressive training procedure that uses images of increasing resolution to train GANs. StyleGAN[8] is one of the latest image generation technologies, which maps latent variables to style variables (i.e., global effects). StyleGAN consists of a progressively growing style-based generator and discriminator. On this basis, Karras et al.[25] analyzed the deficiencies of the adaptive instance normalization (AdaIN) method in StyleGAN and optimized the quality of generated images.
Differing from the aforementioned studies that focus on image generation by mapping from the latent space to the data space, Bi-GAE is a GAN-based auto-encoder that considers the bidirectional mapping between the data and the latent space during decoding and encoding, mainly aiming at improving the feature representational capability in encoding.
2.2 Unsupervised Auto-Encoders
Variational auto-encoders (VAEs)[26] have become a hot topic because of their precise theoretical foundations, ideal training stability, and insightful representations. Recent studies on VAEs focus on disentanglement quantification[27] and different distributions in the latent space[28]. Combining VAEs with generative models is popular in recent AEs[14, 29, 30]. For traditional generative models, IAF-VAE[29] combines VAE with inverse auto-regressive flow to enhance representation in encoding. As for the combination of GAN and VAE, AAE[14] utilizes GAN to make the encoded latent space follow a normal distribution, while introspective VAE (IntroVAE)[30] embeds GAN in the encoder to realize auto-encoding by learning the distribution of the latent space. However, most of these studies do not consider bidirectional optimization between the generation and the encoding in the same training process. Although some AEs, such as BiGAN, achieve the co-training of the generation and the encoding, the lack of cycle-consistency optimization limits the further improvements in feature learning capabilities.
As summarized in Table 1, Bi-GAE differs from the existing studies in three aspects. First, for common generative models such as image generators (e.g., WGAN and StyleGAN) or image-to-image transformers (e.g., CycleGAN), Bi-GAE is a bidirectional auto-encoder that considers the generation and the encoding between the data space and the latent space, mainly aiming at improving the feature representational capability in encoding. Second, some adversarial AEs (e.g., AAE and ALAE) do not implement the bidirectional optimization of decoders and encoders, which means that these AEs cannot perform the bidirectional learning of decoders and encoders to achieve the independent optimization of generation and representation during the same training process. In contrast, Bi-GAE achieves both the joint and separate bidirectional optimization of the decoder and encoder. Third, compared with bidirectional AEs such as BiGAN, Bi-GAE considers distribution cycle-consistency optimizations (CCO) in both the latent space and the data space, and defines the loss terms of CCO from the distribution discrepancy between the real and reconstructed spaces instead of element-level errors. Moreover, we theoretically prove that these optimizations are effective for improving the feature learning ability of encoders and generators.
Table 1. Comparison of Existing StudiesModel Bidirectional Mapping Cycle-Consistency Optimization Realization SIT OFR Space Emb. Str. Loss WGAN[18] × × × × × × LSGAN[10] × × × × × × StyleGAN[8] × × × × × × CycleGAN[2] d-d × × Data GAN Element-level AAE[14] d-l × ✓ Data, latent GAN Space-level ALAE[15] d-l × ✓ Data, latent × Element-level IntroVAE[30] d-l × ✓ Latent × Space-level BiGAN[11] d-l ✓ × × × × BiGAN-QP[31] d-l ✓ ✓ Data, latent × Element-level Bi-GAE (ours) d-l ✓ ✓ Data, latent GAN Space-level Note: 1) d-d and d-l stand for the bidirectional mapping between the data space and another data space, and between the data space and the latent space respectively. 2) SIT and OFR stand for simultaneously independent training and an additional scheme for optimizing feature representation respectively. 3) Space, Emb. Str., and Loss stand for the space, the embedded structure in the framework, and the added loss term respectively for cycle-consistency optimization; ``data" and ``latent" mean making the optimization on the data and the latent space respectively; element-level and space-level mean the loss term from the direct errors between elements (e.g., MSE and MAE) and from the distribution discrepancy between the two spaces (e.g., maximum mean discrepancy (MMD), Wasserstein distance and evidence lower bound objective (ELBO)), respectively. 3. Preliminaries
The design of Bi-GAE is inspired by BiGAN[11] and WGAN[18]. In this section, we introduce the basic idea of BiGAN and the concept of Wasserstein distance in WGAN.
3.1 BiGAN
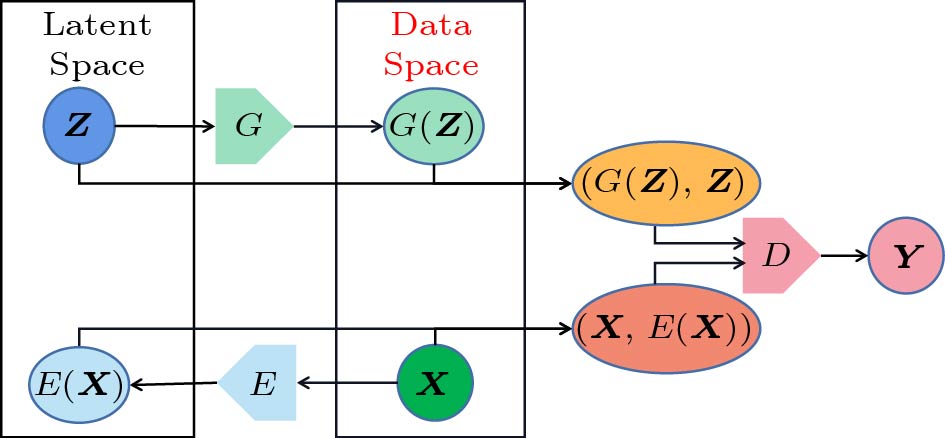
Let X, Z, {{{\boldsymbol{\hat{X}}}}} , and {{{\boldsymbol{\hat{Z}}}}} denote the space of real data, real latent, generated data, and encoded latent following the distribution of P_x , P_z , P_g , and P_e respectively. Meanwhile, let Y denote the space of the decision of the discriminator in GAN-based architectures with the distribution of P_y . As shown in Fig.1, BiGAN consists of a generator {G}:{\boldsymbol{Z}} \rightarrow {\boldsymbol{\hat{X}}} , an encoder {E}:{\boldsymbol{X}} \rightarrow {\boldsymbol{\hat{Z}}} , and a discriminator {D}:({\boldsymbol{X}},\;{\boldsymbol{Z}})\rightarrow {\boldsymbol{Y}} . Abstractly, D estimates the distribution of P_y as the probability density function P_y^{D} , and the computation in G and E is expressed as:
\begin{aligned} {\boldsymbol{\hat{X}}}&={G}\left({\boldsymbol{Z}}\right),\\ {\boldsymbol{\hat{Z}}}&={E}\left({\boldsymbol{X}}\right). \end{aligned} Differing from the AEs with the sequential training process of the encoder and the decoder, BiGAN is a representational and generative auto-encoder, which introduces a joint training mechanism to realize the bidirectional optimization of G and E.
When training, let x and z denote the samples of space X and Z, respectively. BiGAN inputs data samples x to E and latent samples z to G concurrently, and then BiGAN outputs the encoding results ( \hat{z}=E(x) ) and generating results ( \hat{x}=G(z) ) concurrently. After that, the joint results (x,\;\hat{z}) and (\hat{x},\;z) are inputted to D , and D tends to maximize the discrepancy of the predicted discriminating results \hat{y} between (x,\;\hat{z}) and (\hat{x},\;z) . Specifically, BiGAN tends to maximize P_y^{D}(\boldsymbol Y\rightarrow {\boldsymbol{0}}\;|\;({\boldsymbol{\hat{X}}},\;{\boldsymbol{Z}})) and P_y^{D}(\boldsymbol Y\rightarrow {\boldsymbol{1}}\;|\;({\boldsymbol{X}}, {\boldsymbol{\hat{Z}}})) concurrently. According to the theoretical analysis of Donahue et al.[11], the training objective of Bi-GAN is defined as:
\begin{aligned} \begin{aligned}[b] \mathop{\min} \limits_{G,\;E} \mathop{\max} \limits_{D} &\{\mathbb{E}_{{x}\sim P_x}(\log D({x},\;E({x})))+\\& \mathbb{E}_{{z} \sim P_z}(\log{(1-D(G({z}),\;{z}))})\}{.} \end{aligned} \end{aligned} (1) 3.2 WGAN
To overcome the invalid gradient problem in (1) as discovered by Arjovsky et al.[18], we leverage the Wasserstein distance W in WGAN[18] to estimate the discrepancy between the joint distributions ({\boldsymbol{X}},\;{\boldsymbol{\hat{Z}}}) and ({\boldsymbol{\hat{X}}},\;{\boldsymbol{Z}}) . The Wasserstein distance stabilizes the training process and intensifies the convergence of Bi-GAE.
Let {P}_{g_\theta} and {P}_x denote the distribution of the data space generated by G with parameter \theta and the real data space respectively. The Wasserstein distance W between {P}_{x} and {P}_{g_\theta} provides a valid gradient in any case. In practice, WGAN proposes an approximation of W , namely \hat{W}\left({P}_{x},\;{P}_{g_\theta}\right) as:
\hat{W}\left({P}_{x},\;{P}_{g_\theta}\right)={\underset{{x} \sim {P}_{x}}{\mathbb{E}} {(D({x}))}-\underset{{z} \sim {P}_{z}}{\mathbb{E}}{(D({g_\theta({z})}))}}, where \mathbb{E}(\ ) denotes the expectation function, and g_\theta(\cdot) and D(\cdot) are the output of {G} and D respectively. Specifically, D matches a parameterized family of 1 - \text{Lipschitz} functions. We use WGAN-GP[9], which introduces a gradient penalty (GP) term to implement the 1-Lipschitz constraint. On this basis, in Bi-GAE, we use (2) to approximate the Wasserstein distance of the joint distribution.
As proved by Arora et al.[32], WGAN also suffers from the nearly convergent problem of the discriminator (i.e., D). This means that the GAN may not have enough capacity to approximate the Wasserstein distance when D is close to convergence. To address this issue and further optimize the feature representation, we embed an MMD-based GAN in Bi-GAE as described in Subsection 4.3.
4. Method
4.1 Basic Idea
Our goal is to design an unsupervised generative auto-encoder that simultaneously achieves the joint optimization of decoding and encoding. Specifically, given the limitations of BiGAN, we make three major modifications in Bi-GAE.
First, we introduce the Wasserstein distance to Bi-GAE to guarantee the valid gradient computation and the convergence of the training process. To estimate the Wasserstein distance of the joint distributions, we design two convolutional blocks for feature extraction in Bi-GAE.
Second, we embed an MMD-based GAN structure to intensify the feature learning capability of Bi-GAE and further enhance its convergence. We theoretically prove the optimization of the feature representation and convergence of Bi-GAE in Subsection 4.3.
Third, we design two additional loss terms to optimize the representation of the encoder E and the generation of the decoder G , respectively, and constrain cycle-consistency by enabling information expansion during the decoding and encoding. All these expansions effectively guide the joint optimization of the bidirectional mapping between the decoder and the encoder, further improving the feature representational capability.
4.2 Architecture of Bi-GAE
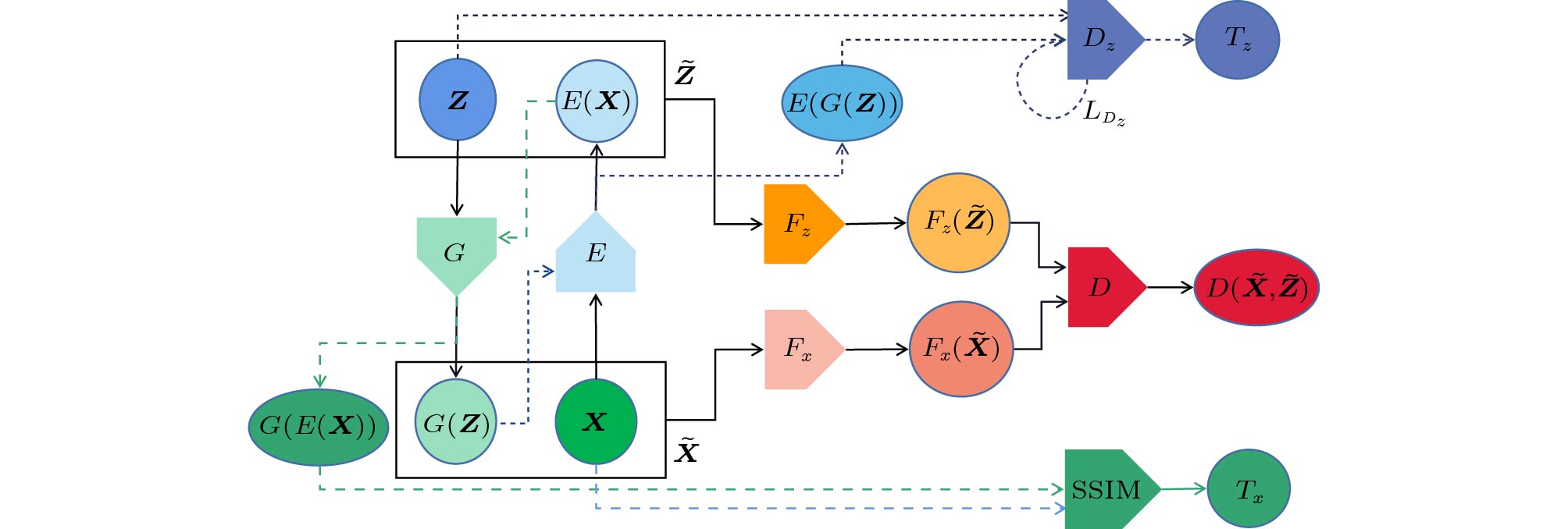
Fig.2 shows the overall architecture of Bi-GAE. Similar to BiGAN, Bi-GAE consists of the generator G , encoder E, and discriminator D. In addition, to implement the three modifications mentioned in Subsection 4.1, we introduce four blocks in Bi-GAE: 1) an SSIM-based block SSIM to compute the additional loss term T_x for G , 2) a discriminator D_z in the embedded GAN, and 3) two convolutional blocks F_x and F_z to extract features from the data space and the latent space, respectively.
Let X, Z, {{{\boldsymbol{\hat{X}}}}} , and {{{\boldsymbol{\hat{Z}}}}} denote the space of real data, real latent, generated data, and encoded latent, respectively. Meanwhile, x and z denote the samples from spaces X and Z respectively. On this basis, we express the generalized data space as {\boldsymbol{\tilde{X}}}=\left({\boldsymbol{X}},\;{\boldsymbol{\hat{X}}}\right) which includes the real and generated data spaces. Similarly, the generalized latent space is expressed as {\boldsymbol{\tilde{Z}}}=\left({\boldsymbol{Z}},\;{\boldsymbol{\hat{Z}}}\right) . Then the main training procedure of Bi-GAE consisting of three steps is described as follows.
In step 1, we input data samples x to E and latent samples z to G concurrently, and compute \hat{z}=E(x) and \hat{x}=G(z) . Therefore, we get \tilde{x}=\left(x,\;\hat{x}\right) (i.e., samples from the generalized data space) and \tilde{z}=\left(\hat{z},\;z\right) (i.e., samples from the generalized latent space).
In step 2, we input \tilde{x} to F_x and \tilde{z} to F_z and calculate {F_x(\tilde{x})} and {F_z(\tilde{z})} as the features of the data space and the latent space respectively.
In step 3, we input the concatenated result (F_x(\tilde{x}),\;F_z(\tilde{z}))=((F_x(x),\;F_z(\hat{z})),(F_x(\hat{x}),\;F_z(\hat{z}))) to D to compute the Wasserstein distance as:
\begin{aligned} \hat{W}(\tilde{x},\;\tilde{z})=D(F_z(\hat{z}),\;F_x(x))-D(F_z(z),\;F_x(\hat{x})). \end{aligned} (2) As for the two additional loss terms T_x and T_z for G and E respectively, we introduce the SSIM-based block and the block D_z . Let {\boldsymbol{\check{X}}} and {\boldsymbol{\check{Z}}} denote the space of reconstructed data and reconstructed latent following the distribution of P_{\check{x}} and P_{\check{z}} respectively. Given encoding results \hat{z}=E(x) , we compute the reconstruction results of x as \check{x}=G(E(x)) . Given \hat{x}=G(z) , we compute the reconstruction results of z as \check{z}=E(G(z)) . For the generator, we input samples (x,\;\check{x}) to the SSIM block to compute T_x . For the encoder, T_z is computed by the embedded GAN consisting of E, G and D_z . Specifically, we input samples (z,\;\check{z}) to the D_z block to estimate the maximum mean discrepancy (MMD) between P_z and P_{\check{z}} , and finally compute T_z .
To improve the computation performance of Bi-GAE, the embedded GAN shares the parameters with {G} and E in the training process. In addition, this sharing mechanism ensures that the embedded GAN and other components in Bi-GAE can converge at the same time.
4.3 Optimizing Feature Learning and Enhancing Convergence
Optimizing feature learning through a stable convergent training process has always been a challenge for BiGAN. The optimization of Bi-GAE is reflected in two aspects: 1) introducing the Wasserstein distance in Bi-GAE to ensure a continuous valid gradient during the Bi-GAE training; 2) embedding MMD-based GAN ( D_z ) for further optimization on the lower bound of the feature representational capability, especially when facing the near-convergence problem.
4.3.1 Introducing Wasserstein Distance
Given \hat{W}(\tilde{x},\;\tilde{z}) between (x,\;\hat{x}) and (z,\;\hat{z}) , we define the loss function L_{{DF}} to train D, {F_x} , and {F_z} as:
\begin{aligned} \begin{aligned} L_{{DF}}=&\dfrac{1}{n_\text{b}}\left(-\hat{W}(\tilde{x},\;\tilde{z})\right)+\\&\lambda \dfrac{1}{n_\text{b}}\underbrace{\left(\left(\left\|\nabla_{\dot{{x}},\;\dot{{z}}} D(\dot{{x}},\;\dot{{z}})\right\|_{2}-1\right)^{2}\right)}_{\text{\small GP term}}, \end{aligned} \end{aligned} (3) where n_\text{b} is the batch size, \dot{x}=\epsilon x+(1-\epsilon)\hat{x} , \dot{z}=\epsilon z+(1-\epsilon)\hat{z} , and the GP term enforces D to obey the 1-Lipschitz constraint. As for E and G, the loss function L_{{EG}} is correspondingly defined as:
\begin{aligned} L_{{EG}}= & \dfrac{1}{n_\text{b}}(D(F_z(\hat{z}),\;F_x(x))-\\ &D(F_z(z),\;F_x(\hat{x}))+\sigma T_x), \end{aligned} (4) where \sigma is a coefficient and T_x is the additional loss term of G to achieve information expansion in generation which is described in Subsection 4.4.
4.3.2 Embedding an MMD-Based GAN
As mentioned in Subsection 3.2, the nearly convergent problem of D occurs when \hat{W}(\tilde{x},\;\tilde{z})\approx 0 . To overcome this limitation, an MMD-based GAN is embedded in Bi-GAE, which consists of E, G, and D_z . Since the Wasserstein distance is a special case (i.e., linear kernel) of maximum mean discrepancy (MMD)[17], we utilize MMD with a high-order matching Gaussian kernel to further optimize the representation of Bi-GAE. Let X and {\boldsymbol{\hat{X}}} denote the real data space and the generated data space with distribution P_x and P_{\hat{x}} respectively, while Z and {\boldsymbol{\hat{Z}}} denote the real latent space and the encoded latent space with distribution P_z and P_{\hat{z}} respectively. The MMD M between the joint distribution of ({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}) and ({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}) is defined as:
\begin{aligned} \begin{aligned} & M(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))\\=&\mathop{\max} \limits_{f}\{ \mathbb{E}(f({\boldsymbol{\hat{Z}}}, {\boldsymbol{X}})) - \mathbb{E}(f({\boldsymbol{Z}}, {\boldsymbol{\hat{X}}}))\}, \end{aligned} \end{aligned} (5) where \mathbb{E}(\ ) denotes the expectation function, and \{f\} is a set of continuous functions. Then, when D is close to convergence, we can derive that:
0 < M(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))\leqslant \upsilon, where \upsilon is a threshold.
4.3.3 Analyzing the Feature Learning of Bi-GAE
Let x_i , \hat{x}_i , z_i , and \hat{z}_i denote the samples from X, {\boldsymbol{\hat{X}}} , Z, and {\boldsymbol{\hat{Z}}} respectively. When D is close to convergence, we derive that M(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),\;({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))\leqslant \upsilon . Then, we theoretically analyze the feature learning capability of Bi-GAE and derive the quantitative analysis of the representation performance with and without the embedded GAN respectively.
Lemma 1. If M({\boldsymbol{\hat{Z}}},\;{\boldsymbol{Z}})=\overline{f\left(\hat{z}_{i}\right)}-\overline{f\left({z}_i\right)}=\sigma>0 and M({\boldsymbol{X}},\;{\boldsymbol{\hat{X}}})=\overline{g\left(x_{i}\right)}-\overline{g\left(\hat{x}_i\right)}=\epsilon>0 , then {M}(({\boldsymbol{\hat{Z}}}, \;{\boldsymbol{X}}),\;({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))=\max\{\sigma,\; \epsilon\}.
Proof.
\begin{aligned}[b] {M}(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),\;({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))=\;&{M}(({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}),\;({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}))\\=\; &\overline{f_0(z_i,\;\hat{x}_i)}-\overline{f_0(\hat{z}_i,\;x_i)}\\=\; &\overline{f_1(z_i|\hat{x}_i)}-\overline{f_{1}(\hat{z_i}|x_i)}. \end{aligned} (6) The derivation in (6) means that f_0(z_i,\;\hat{x}_i) can be represented by f_1(z_i|\hat{x}_i) , if we consider \hat{x}_i as the condition of z_i . Then, we further derive that:
\begin{aligned} \begin{aligned} &{M}(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),\;({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))\\=\;&\overline{f_1(z_i|\hat{x}_i)}-\overline{f_{1}(\hat{z_i}|x_i)}\\=\;& \overline{f_1(z_i|\hat{x}_i)}-\overline{f_1(\hat{z_i}|\hat{x_i})}+\overline{f_1(\hat{z_i}|\hat{x_i})}-\overline{f_1(\hat{z_i}|x_i)}\\\leqslant\; & |\overline{f_{1}(z_i|\hat{x}_i)}-\overline{f_{1}(\hat{z}_i|\hat{x}_i)}|+|\overline{f_{1}(\hat{z}_i|\hat{x}_i)}-\overline{f_{1}(\hat{z}_i|x_i)}|.\\ \end{aligned} \end{aligned} (7) We assume that P_{\hat{x}} is almost equivalent to P_{x} when the network is nearly convergent, and then we derive: |\overline{f_{1}(\hat{z}_i|\hat{x}_i)}-\overline{f_{1}(\hat{z}_i|x_i)}|\approx 0 in (7). Since f_{1}(z_i|\hat{x}_i) and f_{1}(\hat{z}_i|\hat{x}_i) have the same condition, we rewrite f_1(\cdot|\hat{x}_i) as f(\cdot) , and finally we prove that:
\begin{aligned} {M}(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),\;({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))&=|\overline{f(z_i)}-\overline{f(\hat{z}_i)}|+0=\sigma. \end{aligned} Similarly, we can prove that {M}(({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}),\;({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}))\leqslant \epsilon. Therefore, {M}(({\boldsymbol{Z}},\;{\boldsymbol{\hat{X}}}),\;({\boldsymbol{\hat{Z}}},\;{\boldsymbol{X}}))=\max \{\sigma, \epsilon\} .
□ As we can see, the MMD value of joint space is the maximum value of the two MMD values namely: 1) the MMD between the real and generated spaces of data and 2) the MMD between the real and generated spaces of latent. Therefore, if and only if the Bi-GAE becomes convergent on both data space and latent space in terms of MMD separately, Bi-GAE ensures the convergence on the joint spaces in terms of MMD, and vice versa. Meanwhile, a lower MMD indicates that the distributions of the two spaces are more similar. This corresponds to a better feature learning performance for mapping models (e.g., E and G ). Thus, the overall feature learning capability of Bi-GAE depends on the feature learning capability of E and G which is quantified as M({\boldsymbol{\hat{Z}}},\;{\boldsymbol{Z}}) and M({\boldsymbol{X}},\;{\boldsymbol{\hat{X}}}) , respectively.
Lemma 2. \forall\;{{{space}}\;{\boldsymbol{A}}, {\boldsymbol{B}}} , we get M({\boldsymbol{A}}, {\boldsymbol{B}})= M(\psi({\boldsymbol{A}}), \;\psi({\boldsymbol{B}}))=\tau, where \psi(\cdot) is a continuous function that can be estimated by a neural network.
Proof. Let \mathbb{E}(\cdot) denote the expectation function. Assuming \exists \rho (continuous functions), it has \mathbb{E}(\rho(\psi({\boldsymbol{A}})))- \mathbb{E}(\rho(\psi({\boldsymbol{B}}))) >\tau . Let \kappa=\rho\times \psi , \mathbb{E}(\kappa({\boldsymbol{A}}))- \mathbb{E}(\kappa({\boldsymbol{B}})) > \tau = M({\boldsymbol{A}}, {\boldsymbol{B}}), which contradicts the definition of MMD. Thus, we get \mathbb{E}(\rho(\psi({\boldsymbol{A}})))-\mathbb{E}(\rho(\psi({\boldsymbol{B}})))\leqslant \tau . Therefore, we prove that {M}(\psi({\boldsymbol{A}}),\;\psi({\boldsymbol{B}}))=\mathop{\max} \limits_{\rho}(\mathbb{E}(\rho(\psi({\boldsymbol{A}})))-\mathbb{E}(\rho(\psi({\boldsymbol{B}}))))=\tau.
□ Lemma 2 implies that MMD is stable for continuous functions \psi (e.g., G and E trained in Bi-GAE). Since the embedded GAN in Bi-GAE is based on MMD, we can estimate the cycle-consistency between the distributions of real and reconstructed latent/data spaces as M(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}}) / M({\boldsymbol{X}},\;G(E({\boldsymbol{X}}))) . Then, we can derive the upper bound of M(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}}) (i.e., the lower bound of distribution consistency) according to Lemma 1 and Lemma 2.
Theorem 1. When D is nearly convergent, the upper bound of M(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}}) without D_z tends to be 2\times\upsilon .
Proof. According to Lemma 2, we derive that:
\begin{aligned} &M(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}})\\\leqslant\;& M(E(G({\boldsymbol{Z}})),\;E({\boldsymbol{X}}))+M(E({\boldsymbol{X}}),\;{\boldsymbol{Z}})\\=\;& M({\boldsymbol{X}},\;G({\boldsymbol{Z}}))+M(E({\boldsymbol{X}}),\;{\boldsymbol{Z}}). \end{aligned} Then, we can derive the upper bound of M(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}}) without D_z according to Lemma 1:
\begin{aligned} &M(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}}) \\\leqslant \;&M({\boldsymbol{X}},\;G({\boldsymbol{Z}}))+M(E({\boldsymbol{X}}),\;{\boldsymbol{Z}})\\= \;&\epsilon+\sigma \leqslant 2\times \max\{\epsilon,\;\sigma\}\leqslant 2\times \upsilon. \end{aligned} Similarly, we can derive that M({\boldsymbol{X}},\;G(E({\boldsymbol{X}}))) \leqslant M({\boldsymbol{X}},\;G({\boldsymbol{Z}}))+M({\boldsymbol{Z}},\;E({\boldsymbol{X}}))\leqslant 2\times\upsilon.
□ By embedding D_z in Bi-GAE, according to (5) and Lemma 2, when D_z is convergent, the optimized MMD M' satisfies:
\begin{aligned} \begin{aligned} & M'(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}})\\ \leqslant\;& M'({\boldsymbol{X}},\;G({\boldsymbol{X}}))+M'(E({\boldsymbol{X}}),\;{\boldsymbol{Z}}) \leqslant \upsilon, \\ &M'(G(E({\boldsymbol{X}})),\;{\boldsymbol{X}})\\\leqslant\;& M'({\boldsymbol{X}},\;G({\boldsymbol{Z}}))+M'(E({\boldsymbol{X}}),\;{\boldsymbol{Z}})\leqslant \upsilon. \end{aligned} \end{aligned} (8) The derivation in (8) means that the upper bound of both M'(E(G({\boldsymbol{Z}})),\;{\boldsymbol{Z}}) and M'(G(E({\boldsymbol{X}})),\;{\boldsymbol{X}}) can be reduced to \upsilon . This reduction verifies that the embedded GAN in Bi-GAE can improve the information expansion between X and E({\boldsymbol{X}}) , and between Z and G({\boldsymbol{Z}}) . According to the above theoretical analysis, we can conclude two important insights presented in Theorem 2 and Theorem 3.
Theorem 2. By introducing MMD with high-order Gaussian kernels, the optimizations of feature learning and convergence of Bi-GAE are equivalent to optimizing the lower bound of the feature learning capability of E and G respectively, when D is nearly convergent.
Theorem 3. Optimizing the cycle-consistency between the distributions of the real and the reconstructed data/latent space can improve the lower bound on the feature learning capability of G / E , especially when the models face the near-convergence problem.
Therefore, the embedded MMD-GAN framework achieves two major optimizations of Bi-GAE as follows.
Enhancing Convergence. Before D converges, we introduce the Wasserstein distance in Bi-GAE to guarantee a stable training process with convergence. When D is trapped in the near-convergence problem, according to Lemma 1, we introduce terms T_z and T_x to Bi-GAE as defined in (10) and (13) respectively, which can enhance the convergence of E and G respectively. These added structures enhance the convergence of Bi-GAE.
Improving Representation. One of the goals of Bi-GAE is to enhance semantic-relevant representation capability in the encoding. According to (8), the embedded GAN in Bi-GAE achieves information expansion in the encoding by reducing M(E(G({\boldsymbol{Z}}),\;{\boldsymbol{Z}})) to improve semantic-relevant representations.
Wang et al.[33] proved that the MMD loss consists of repulsive terms L^{\text{rep}} and attractive terms L^{\text{att}} . They also proposed a single bounded Gaussian kernel method with kernel function k_\text{F} to reduce computation. We compute \check{z}=E(G(z)) and let Q_{\check{z}}=P(\check{z}|E,\;G) denote the conditional distribution of \check{z} . Therefore, the loss functions L_{D_z} for {D_z} and L_{{EG}_z} for E and {G} are defined as:
\begin{aligned} \begin{aligned} &L_{D_z}\\=\;&\mathbb{E}_{z,\;z'\sim P_z}\left(k_{\text{rep}}\left({{y_z}},\;{ {y_{z'}}}\right)\right) -\mathbb{E}_{\check{z},\;\check{z}'\sim Q_{\check{z}}}{\left(k_{\text{rep}}\left({y_{\check{z}}},\;{y_{\check{z}'}}\right)\right)},\\ &L_{{EG}_z}\\=\;&\mathbb{E}_{{z},\;{z}' \sim P_z}\left(k_{\text{att}}\left({y_z},\;{ y_{{z}'}}\right)\right)+\mathbb{E}_{\check{z},\;\check{z}'\sim Q_z}\left(k_{\text{att}}\left({y_{\check{z}}},\; {y_{\check{z}'}}\right)\right)-\\ \;& 2 \mathbb{E}_{z\sim P_{z},\;\check{z}\sim Q_{\check{z}}}\left(k_\text{F}({y_z},\; {y_{\check{z}}})\right), \end{aligned} \end{aligned} (9) where {y_z}=D_z(z) , {y_{z'}}=D_z(z') , {y_{\check{z}}}=D_z(\check{z}) , {y_{\check{z}'}}= D_z(\check{z}').
k_{\text{rep}}({a},\;{b})=\left\{\begin{aligned}& {\rm e}^{-\tfrac{1}{2 \sigma^{2}} \max \left(\|{a}-{b}\|^{2},\;b_{l}\right)}, &{a},\;{b} \in\{{y_{\tilde{z}}}\}, \\& {\rm e}^{-\tfrac{1}{2 \sigma^{2}} \min\left(\|{a}-{b}\|^{2},\;b_{u}\right)}, & {a},\;{b} \in\{{y_z}\}, \end{aligned}\right. and
k_{\text{att}}({a},\;{b})=\left\{\begin{aligned} &{\rm e}^{-\tfrac{1}{2 \sigma^{2}} \max \left({\|{a}-{b}\|}^{2},\;b_{l}\right)}, & {a},\;{b} \in \{ y_{z}\} \text { or } \{{y_{\check{z}}}\}, \\& {\rm e}^{-\tfrac{1}{2 \sigma^{2}} \min \left(\|{a}-{b}\|^{2},\;b_{u}\right)}, & {a} \in\{{y_z}\},\;{b} \in\{{y_{\check{z}}}\}. \end{aligned}\right. In addition, we utilize the \text{L}_2 loss {L}^{\text{l}_{2}} between z and \check{z} to avoid excessive element-level errors. Therefore, the term T_z for the latent space is defined as:
\begin{aligned} \begin{aligned} &T_z= \alpha_1 L_{{EG}_z}+\dfrac{1}{n_\text{b}}(1-\alpha_1){L}^{\text{l}_{2}}(z, \check{z})\text{,} \end{aligned} \end{aligned} (10) where \alpha_1 is a weight coefficient.
4.4 Promoting Generation to Follow Human Visual Models
In addition to optimizing feature representation in the encoding, the generator of Bi-GAE also attempts to achieve competitive generative capabilities. Following the insights proposed in Theorem 3, we can achieve that by extracting high-level features of the distribution of the data space and exploiting these features to optimize the cycle-consistency on the data space. Therefore, Bi-GAE designs a term between the real and the reconstructed data space.
Let FR(\cdot) denote the generic high-level feature representation for the data space, and then we model the additive cycle-consistency optimization term of the data space ( T_x for short) as:
T_{x} = \|FR({\boldsymbol{X}})-FR({\boldsymbol{\check{X}}})\|^{2}_{2}, where X and {\boldsymbol{\check{X}}}=G(E({\boldsymbol{X}})) denote the real and the reconstructed data space respectively. To quantify the high-level feature representation of the data distribution, the perceptual loss[21, 34] is a widely-used metric. The core mechanism of the perceptual loss is utilizing the pre-trained convolutional neural networks (CNNs) to extract perceptual features of the data space. For example, Gatys et al.[34] found that a pre-trained visual geometry group network (VGGNet) is a classical perceptual loss function. However, Liu et al.[35] proved that the pre-trained weights of perceptual loss networks may lead to gradient exploding or vanishing when training the generative model. For our cycle-consistency optimization, we model the effect of these unstable gradients on Bi-GAE as follows.
Firstly, we estimate the generic perceptual loss term between X and {\boldsymbol{\check{X}}} as:
\begin{aligned} l^{\theta^c,j}_{\rm per}&=(\theta^{c}_j(\check{x})-\theta^{c}_j(x))^2,\\ \theta^{c}_j(x) &= \boldsymbol\omega_j\cdot \theta^{c}_{j-1}(x) + b_j, \end{aligned} where x and \check{x} denote the samples from spaces X and {\boldsymbol{\check{X}}} , respectively, and \theta^{c}_j(\cdot) denotes the output of the j -th convolution layer ( \theta^{c}_j ) in the perceptual loss network. For \theta^{c}_j , let k_j , c_j , and o_j denote the kernel size, the number of input channels, and the number of output channels, respectively. Then, we define \omega_j \in {\cal{R}}^{o_j\times(k^2_j\times c_j)} as the weight of \theta^{c}_j .
Following the research in [36], we estimate the variance of the FR({\boldsymbol{X}}) output after the J convolution layers when using the perceptual loss network as FR(\cdot) :
{Var}\left(FR({\boldsymbol{X}})\right)\approx{Var}\left(\theta^{c}_1(x)\right)\left(\prod\limits_{j=2}^{J} \dfrac{1}{2} k^2_jc_j {Var}\left(\omega_{j}\right)\right), where Var(\cdot) denotes the variance function. Therefore, the variance of the perceptual loss in T_x is upper bounded as:
\begin{aligned} \begin{aligned} &{Var}\left(\left(FR({\boldsymbol{\check{X}}})-FR({\boldsymbol{X}})\right)\right)\\ = &{Var}\left(FR({\boldsymbol{\check{X}}})\right) + {Var}\left(FR({\boldsymbol{X}})\right) - 2 {Cov} \left(FR({\boldsymbol{\check{X}}}),\;FR({\boldsymbol{X}})\right)\\ \leqslant & ({Var}\left(\theta^{c}_1(x)\right) + {Var}\underbrace{\left(\theta^{c}_1\left(G\left(E(x)\right)\right)\right))\left(\prod_{j=2}^{J} \dfrac{1}{2} k^2_jc_j {Var}\left(w_{j}\right)\right)}_{\text{\small may lead to gradient vanishing or exploding}}, \end{aligned} \end{aligned} (11) where Cov(\cdot,\;\cdot) denotes the covariance function. Then, it can be found that some perceptual feature representations are implicit in the pre-trained weights of the perceptual loss networks, which introduces potential gradient vanishing/exploding to the training of the generator/encoder of Bi-GAE. These unstable gradients can 1) confuse the feature learning capabilities in the generator and the encoder, and 2) have a negative effect on the convergence of Bi-GAE when training the model.
Essentially, these negative effects are attributed to some perceptual feature representations that are learned by pre-training on public datasets (e.g., imageNet), but are not adapted to the training of our model. To mitigate this effect, Bi-GAE considers an interpretable high-level feature metric instead of a pre-trained network. Specifically, we choose the structural similarity index measure (SSIM)[37], which includes human visual metrics of luminance, contrast and structure. When training {G} and {E} with data samples x , we compute \check{x}=G(E(x)) . Let (s_\text{i}\times s_\text{i}) denote the size of x and let m be the number of Gaussian filters; hence we compute multi-scale SSIM (MS-SSIM) as:
\begin{aligned} {{{MS\text{-}SSIM}}}(x,\;\check{x})={l_{m}}^{\gamma \times m}(x,\;\check{x}) \times \prod_{j=1}^{m} cs_{j}^{\eta_{j}}(x,\;\check{x}). \end{aligned} (12) We set the size of the j -th filter to \left(\dfrac{s_\text{i}}{2^{j-1}}\right)^{2} . l(x,\;\check{x}) and cs(x,\;\check{x}) in (12) are defined as:
\begin{aligned} l(x,\;\check{x})=\dfrac{\left(2 \mu_{x} \mu_{\check{x}}+c_{1}\right)}{\left(\mu_{x}^{2}+\mu_{\check{x}}^{2}+c_{1}\right)},\\ cs(x,\;\check{x})=\dfrac{\left(2 \sigma_{x\check{x}}+c_{2}\right)}{\left(\sigma_{x}^{2}+\sigma_{\check{x}}^{2}+c_{2}\right)}, \end{aligned} where u_x and u_{\check{x}} denote the mean of x and \check{x} respectively; \sigma_x , \sigma_{\check{x}} , and \sigma_{x\check{x}} denote the standard deviation of x and \check{x} , and the covariance between x and \check{x} respectively; c_1 and c_2 are constants. Then, let LMS-SSIM denote the {\text{MS-SSIM}} loss for G , which is defined as:
\begin{aligned} {L}^{{\text{MS-SSIM}}}(x,\;\check{x})= 1-{MS\text{-}SSIM}(x,\;\check{x}). \end{aligned} Similar to the definition of T_z in (10), we introduce a regularization term to avoid excessive element-level errors. In addition, to avoid the over-penalty caused by the \text{L}_2 loss, the term T_x combines {L}^{{\text{MS-SSIM}}} with \text{L}_1 loss {L}^{\text{l}_{1}} as:
\begin{aligned} \begin{aligned} &T_{x}=\left(\alpha_2{L}^{{\text{MS-SSIM}}}\left(x,\;{x}'\right)+(1-\alpha_2){L}^{\text{l}_{1}}(x,\;{x}')\right), \end{aligned} \end{aligned} (13) where \alpha_2 is set to 0.84 by default according to [37].
5. Implementation
Each component in Bi-GAE is implemented based on the source code of DCGAN[12], and the real latent space follows the standardized normal distribution, i.e., {\boldsymbol{Z}}\sim N({\boldsymbol{0}},\;{\boldsymbol{I}}) . Let \theta_E , \theta_G , \theta_D , \theta_{D_z} , and \theta_\text{F}=\{\theta_{F_x},\;\theta_{F_z}\} denote the parameters of E, {G} , D, {D_z} , and \{{F_x},\;{F_z}\} respectively. Correspondingly, we use three custom Adam optimizers with \beta_1=0.5 and \beta_2=0.9 : Adam_{{EG}} for \theta_G and \theta_E , Adam_{{DF}} for \theta_\text{F} and \theta_D , and Adam_{D_z} for {D_z} with learning rates lr_{{EG}} , lr_{{DF}} , and lr_{D_z} respectively. In addition, let n_\text{b} , s_\text{i} , s_\text{l} , N_{\text{GPU}} , and N_{\text{epoch}} denote the batch size, image size, dimension of latent space, the number of used GPUs, and training epochs, respectively. Table 2 lists the configuration of these hyper-parameters in the experiments.
Table 2. Parameter Settings of Bi-GAEResolution n_\text{b} N_{\text{GPU}} N_{\text{epoch}} s_\text{i} s_\text{l} lr_{{DF}} lr_{{EG}} lr_{D_z} \alpha_1 \alpha_2 MNIST {28\times28} 128 1 150 28 80 0.000120 0.00012 0.00008 0.6 0.840 CelebA-HQ {128\times128} 64 1 380 128 128 0.000120 0.00012 0.00009 0.7 0.750 {256\times256} 64 2 400 256 256 0.000150 0.00015 0.00012 0.8 0.720 {512\times512} 32 4 400 512 512 0.000018 0.00018 0.00014 0.8 0.675 Note: 1) This table lists the hyper-parameter settings for the experiments on the dataset MNIST[38] and CelebA-HQ[16], respectively. 2) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset in our implementation. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. Algorithm 1 presents the training procedure of Bi-GAE, which comprises four steps.
Algorithm 1. Training Procedure 1: \theta_{E},\;\theta_{G},\;\theta_{{F}},\;\theta_{D},\;\theta_{D_{z}} \leftarrow \text{Initial parameters}; 2: while (not convergent){ 3: for (i=0 ; i<Iter_{D} ; i++ ){ 4: x \leftarrow n_\text{b}\text{ samples from the data space } {\boldsymbol{X}} ; 5: z \leftarrow n_\text{b}\text{ samples from the latent space } {\boldsymbol{Z}} ; 6: Compute L_{DF} ; update \theta_{\text{F}} , \theta_{D} by {Adam_{{DF}}} ; 7: } 8: x \leftarrow n_\text{b}\text{ samples from the data space } {\boldsymbol{X}} ; 9: z \leftarrow n_\text{b}\text{ samples from the latent space } {\boldsymbol{Z}} ; 10: \check{x} \leftarrow G(E_{\text{ng}}(x)) ; 11: Compute T_x , L_{{EG}} ; update \theta_{E} , \theta_{G} with {Adam_{{EG}}} ; 12: {\bf {for}} (i=0 ; i<Iter_{D_z} ; i++ ){ 13: z \leftarrow n_\text{b}\text{ samples from the latent space } {\boldsymbol{Z}} ; 14: Compute L_{D_z} ; update \theta_{D_z} with {Adam_{D_z}} ; 15: } 16: z \leftarrow n_\text{b}\text{ samples from the latent space }{\boldsymbol{Z}} ; 17: \check{z} \leftarrow E(G_\text{ng}(z)) ; 18: Compute T_z ; update \theta_E using Adam_{{EG}} with lr_{{EG}_{z}} ; 19: } In step 1, we use real data and real latent samples (x,\;z) to train D and \{{F_x},\;{F_z}\} with the loss L_{{DF}} in (3) for Iter_{D} times (lines 3–7). In our experiments, we set Iter_{D} as 4.
In step 2, we use another batch of (x,\;z) to train {G} and E with the loss L_{{EG}} in (4). Given x , we compute \check{x}=G(E_{\text{ng}}(z)) where E executes non-gradient ( \text{ng} ) encoding, and use (x,\;\check{x}) to compute T_x in (13) to train G (lines 8–11).
In step 3, we input a batch of z to train D_z with the loss L_{D_z} in (9) for Iter_{D_z} times ( Iter_{D_z}=4 ) (lines 12–15).
In step 4, we input a batch of z to compute \check{z}=E\left(G_\text{ng}(z)\right) where G executes non-gradient decoding. We use (z,\;\check{z}) to train {E} with the loss function T_z in (10) (lines 16–19).
6. Experiments
6.1 Setup
We train Bi-GAE on two open-source datasets, namely MNIST[38] and CelebA-HQ[16] using four servers with 16 V100 GPU cards with the configurations listed in Table 2. We compare the performance of Bi-GAE and three AEs, namely BiGAN (implemented using the Wasserstein distance in [9] as the loss function), BiGAN-QP, and AAE. To evaluate the representation (decoding) performance of AEs, we use four classical classifiers: support vector machine (SVM)[39], linear discriminant analysis (LDA)[40], random forest (RF)[41], and adaptive boosting (AdaBoost)[42]. In addition, since we introduce the Wasserstein distance in Bi-GAE to overcome the invalid gradient problem in the GAN-based AE frameworks, and WGAN with the GP term[9] is a classical study to apply the Wasserstein distance in the GAN-based generators, we use WGAN as the baseline to evaluate the generation performance in our experiments.
We utilize the Fréchet inception distance (FID)[43] to evaluate the similarity between the generated and real images. In the evaluation of the overall performance, we use FID and SSIM to evaluate the quality of the reconstructed results. Higher SSIM scores or lower FID scores represent better performance. Furthermore, we utilize the recently proposed metric perceptual path length (PPL)[8] to evaluate the disentanglement ability of the tested AEs.
6.2 Representation (Encoding) Performance
In our experiments, we use the encoding results of the four tested AEs as the inputs to the four representative classifiers: SVM ( \gamma=0.05 , C=5 , 1000 iterations), LDA, RF (100 estimators), and AdaBoost (300 estimators), and analyze the accuracy to evaluate the performance of feature representation, especially the performance of semantic-relevancy.
For the MNIST dataset, we use the encoding vectors of 60000 and 10000 images to train and test the classifiers respectively. We use 10 numerals (0–9) as image labels. As for the CelebA-HQ dataset, we conduct experiments on the images with resolutions of 128\times128 , 256\times256 , and 512\times512 , respectively. Specifically, for each of the three resolution settings, we use the encoding vectors of 25000 and 5000 images to train and test the classifiers, respectively. In addition, we set the image labels (16 classes) to the combination of four specific 0–1 image labels (i.e., wearing glasses or not, gender, young or old, smiling or not), where we encode the class ID as the 4-bit binary, for each digit 1 means they have the corresponding label and 0 means they do not have the label. From left to right, the value of each digit corresponds to the label: wearing glasses, male, young, and smiling. For example, 1111 (15) means the class ID of smiling young men wearing glasses, and 0000(0) represents the class ID of unsmiling old women without glasses..
Table 3 shows the average results for the four AEs. On the MNIST dataset, Bi-GAE achieves the best representation performance in RF, AdaBoost, and LDA. On the CelebA-HQ dataset, Bi-GAE achieves the best performance among the four classifiers at the resolutions of 128\times128 , 256\times256 , and 512\times512 . In addition, we observe that the representation performance of Bi-GAE is more stable than that of the other three AEs at different resolutions. These results validate that Bi-GAE facilitates the semantic-relevancy of feature representations. This improvement is attributed to three reasons: 1) the cycle-consistency optimization on the data space and the latent space jointly improves the lower bound of the feature representational capability; 2) the embedded GAN further optimizes the feature representation when D is close to convergence; 3) the term T_z optimizes the robustness of the representation in encoding.
Table 3. Classification Accuracy (%) on the MNIST and CelebA-HQ DatasetsModel MNIST CelebA-HQ 28\times28 128\times128 256\times256 512\times512 SVM RF AdaBoost LDA SVM RF AdaBoost LDA SVM RF AdaBoost LDA SVM RF AdaBoost LDA BiGAN {92.70} {84.83} 70.49 82.33 48.51 40.43 43.63 57.26 48.42 40.69 41.29 61.37 28.26 41.60 35.12 63.67 BiGAN-QP \bf{97.92} 93.44 85.34 91.25 54.99 41.62 40.85 52.97 52.91 38.94 38.15 54.67 30.23 34.81 31.71 48.47 AAE 96.05 {90.64} 60.83 77.39 40.63 41.12 41.92 56.12 31.22 38.88 40.31 58.41 17.34 40.76 31.14 64.12 Bi-GAE (ours) {97.18} \bf{94.09} \bf{86.99} \bf{91.55} \bf{58.73} \bf{55.09} \bf{53.65} \bf{62.19} \bf{54.85} \bf{52.91} \bf{51.10} \bf{68.79} \bf{48.75} \bf{43.72} \bf{42.10} \bf{66.42} Note: 1) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset in our experiments. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. 2) This table lists the accuracy of four classifiers, i.e., SVM, RF, AdaBoost, and LDA when inputting the encoding results of the MNIST and CelebA-HQ datasets. These encoding results are computed by the four different AE models. 3) The bold font represents the highest classification accuracy of a classifier, which is equivalent to the best representation performance among the AE models. 6.3 Generation (Decoding) Performance
On the MNIST dataset, we randomly generate 10000 images from the latent space. On the CelebA-HQ dataset, we generate 5000 images at the resolutions of 128\times128 , 256\times256 , and 512\times512 , respectively. Table 4 list the best FID results of the four AEs to evaluate their generation performance.
Table 4. Generation Performance in Terms of FID Metric on the MNIST and CelebA-HQ DatasetsModel Type FID MNIST CelebA-HQ 28\times 28 128\times128 256\times256 512\times512 BiGAN AE 6.779 {31.580} 41.058 49.002 BiGAN-QP AE 12.290 39.338 57.443 68.371 AAE AE 41.823 44.297 59.189 76.721 Bi-GAE (ours) AE 5.736 26.162 31.223 44.031 WGAN GAN - 20.736 25.473 28.831 Note: 1) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. 2) The generation performance is measured in terms of FID in this table. The bold font represents the lowest FID value of the images generated by different models on the dataset with a specific resolution, which is equivalent to the best generation performance among the models. 3) AE and GA stand for the auto-encoders and the GAN-based generators, which are diverse types of generative models. Compared with BiGAN, BiGAN-QP, and AAE, we observe that Bi-GAE can achieve better generation performance at all the three resolutions, which is closer to the generative capability of WGAN. These results validate that Bi-GAE's generator can retain a more efficient generative power with a trade-off between the generator and the encoder when building bidirectional mapping. The premise of this generative capability is attributed to two points: 1) the term T_x captures the high-level features of the data spaces to facilitate generation, and 2) as proved in (8), cycle-consistency optimization and embedding structure also improve the lower bound of the feature learning capability of the generator in Bi-GAE.
Fig.3 shows the generated images of Bi-GAE on the MNIST dataset and the CelebA-HQ dataset at different resolutions. These generated images contain the main characteristics of the original images, following human visual models. Specifically, the images generated on the MNIST dataset contain handwriting details, while the images generated on the CelebA-HQ dataset capture the overall characteristics of human faces and some distinctive details at different resolutions.
6.4 Overall Performance
In each experiment, on the MNIST dataset, we use 60000 images to train the models and 10000 images to test the reconstruction performance. On the CelebA-HQ dataset, we downscale the images to 128\times 128 , 256 \times 256 , and 512 \times 512 , respectively, and for images with each of the resolutions, we set a train/test split of 25000/5000. We perform each experiment five times.
6.4.1 Convergence Performance of Bi-GAE
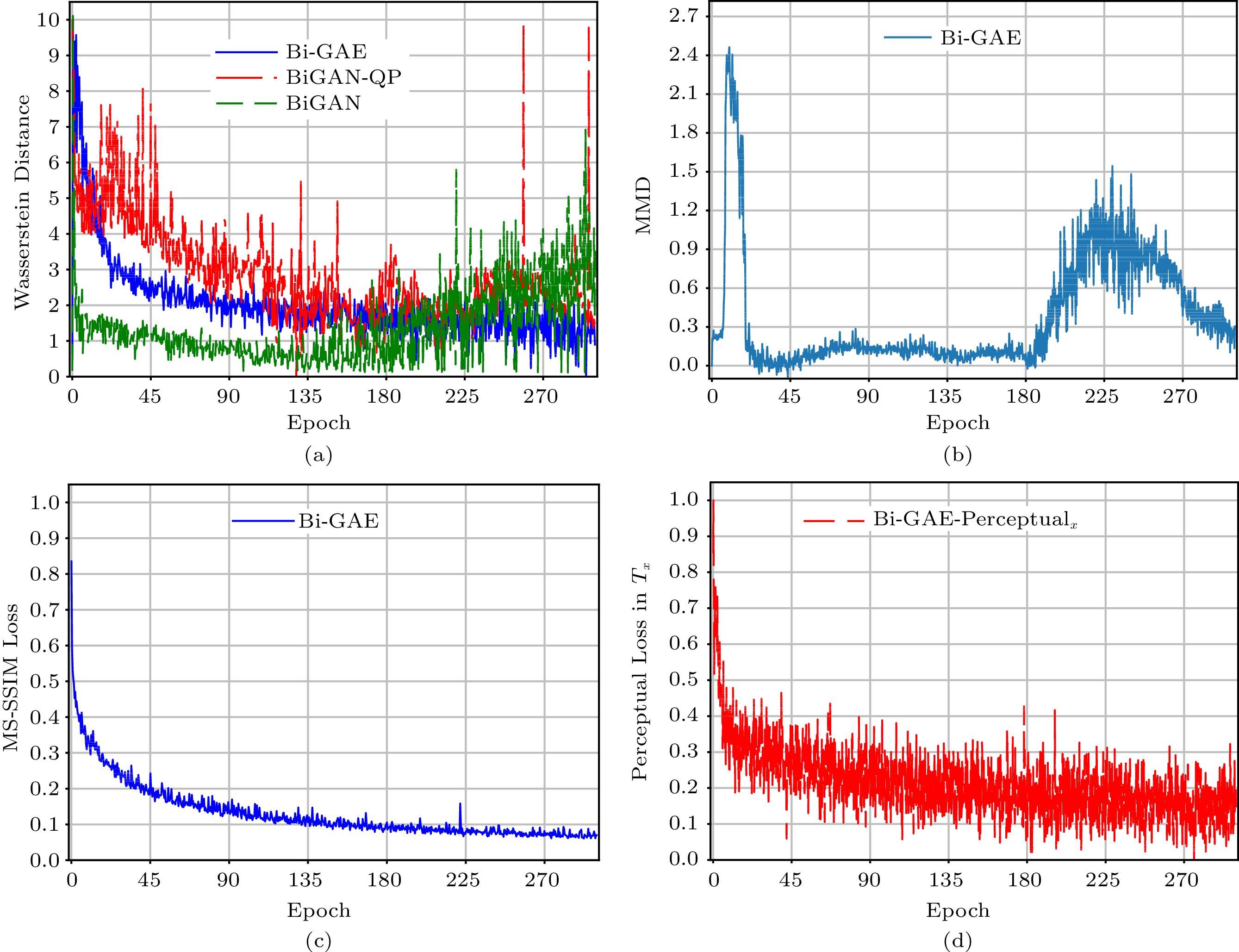
Fig.4(a) shows the curves of the Wasserstein distance (scaled to [0,\;10] ) during the training of Bi-GAE, BiGAN, and BiGAN-QP. We observe that introducing the Wasserstein distance to these models makes them converge. Compared with BiGAN, Bi-GAE overcomes the near-convergence problem of D (occurring at around the 180th epoch as shown in Fig.4(a) and Fig.4(b)). In addition, Bi-GAE's convergence is significantly better than that of BiGAN-QP.
![]() Figure 4. Training of Bi-GAE, Bi-GAE- {\text{perceptual}_x} , BiGAN, and BiGAN-QP on the CelebA-HQ dataset at the resoultion of 256 \times 256 . (a) Training loss curve in terms of the Wasserstein Distance. (b) Training loss curve in terms of the MMD in T_z . (c) Training loss curve in terms of the MS-SSIM in T_x . (d) Training loss curve in terms of the perceptual loss for Bi-GAE- {\text{ perceptual}_x} .
Figure 4. Training of Bi-GAE, Bi-GAE- {\text{perceptual}_x} , BiGAN, and BiGAN-QP on the CelebA-HQ dataset at the resoultion of 256 \times 256 . (a) Training loss curve in terms of the Wasserstein Distance. (b) Training loss curve in terms of the MMD in T_z . (c) Training loss curve in terms of the MS-SSIM in T_x . (d) Training loss curve in terms of the perceptual loss for Bi-GAE- {\text{ perceptual}_x} .This improvement is mainly attributed to the effective convergence enhancement of the generator and the encoder via T_x and T_z respectively. Specifically, Fig.4(b) and Fig.4(c) show the curves of MMD and MS-SSIM loss in the same training process of Bi-GAE which reflect the significant convergence of Bi-GAE in the generation and encoding, respectively. In addition, Fig.4(b) reflects that the MMD-based GAN framework embedded in Bi-GAE has a clear positive effect on overcoming the near-convergence problem (occurring at around the 180th epoch). These results validate the stable convergence properties of Bi-GAE and verify the theoretical property of Bi-GAE proved in Lemma 1.
Furthermore, Fig.4(d) shows the perceptual loss curve (scaled to [0,\;1] ) when using the perceptual loss instead of the MS-SSIM loss in T_x (i.e., Bi-GAE- {\text{perceptual}_x} ). We find that the training process of Bi-GAE- {\text{perceptual}_x} is more oscillating compared with that of the canonical Bi-GAE (in Fig.4(c)). This unstable convergence property of Bi-GAE- {\text{perceptual}_x} illustrates the effect of the unstable gradients when using perceptual loss, as analyzed in Subsection 4.4.
6.4.2 Reconstruction Performance
Table 5 shows the reconstruction performance of the four AEs on the MNIST and CelebA-HQ datasets. We observe that Bi-GAE improves reconstruction capability, especially for high-resolution images. The improvement of SSIM is mainly attributed to the optimization of the term T_x and the stable convergence of Bi-GAE. For FID, the improvement is due to the joint optimization and the information expansion through the two terms T_x and T_z . However, we also find that Bi-GAE performs poorly on low-resolution images. This can be explained by the fact that Bi-GAE is not sufficiently trained on low-dimensional data since it contains more components compared with BiGAN and AAE.
Table 5. Reconstruction Performance in Terms of SSIM and FID on the MNIST and CelebA-HQ DatasetsModel SSIM FID MNIST CelebA-HQ MNIST CelebA-HQ 28\times 28 128\times128 256\times256 512\times512 28\times 28 128\times128 256\times256 512\times512 BiGAN 0.767 0.501 0.505 0.490 8.157 30.750 41.061 47.605 BiGAN-QP 0.782 0.489 0.449 0.396 10.437 38.642 55.353 70.319 AAE 0.926 0.509 0.523 0.512 8.013 40.301 57.472 73.773 Bi-GAE (ours) 0.771 0.504 0.540 0.535 8.416 {25.420} 30.621 45.125 Note: 1) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset in our experiments. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. 2) The reconstruction performance is quantified in terms of SSIM and FID, respectively. The bold font represents the highest SSIM value and the lowest FID value respectively. The highest SSIM value and the lowest FID value are equivalent to the best reconstruction performance among the models, respectively. Fig.5 shows the reconstructed images of Bi-GAE on the MNIST dataset and the CelebA-HQ dataset at the resolutions of 256\times256 , and 512\times512 , respectively. On MNIST, reconstructions look sharp and contain appreciable details. On CelebA-HQ, it can be observed that the images reconstructed by Bi-GAE contain distinctive characteristics that follow human visual models as well as most of the details in the raw images.
6.4.3 Disentanglement Ability
When evaluating the disentanglement ability of the four AEs, the fully PPL is the mainly concerned metric, and an AE achieving a lower PPL score represents that the AE has a better disentanglement ability. As shown in Table 6, Bi-GAE slightly improves the disentanglement ability compared with BiGAN and AAE, while BiGAN-QP is the best. This result reflects that disentanglement is not always equivalent to the overall performance. We should focus on the disentanglement related to the representation.
Table 6. Disentanglement Ability on CelebA-HQModel PPL Full End BiGAN 13.868 {4.735} BiGAN-QP 3.598 3.031 AAE 14.756 6.751 Bi-GAE (ours) {11.368} 5.245 Note: 1) We use the images in the CelebA-HQ dataset at the resolution of 256 \times 256 to evaluate the disentanglement ability of different models. 2) The disentanglement ability is quantified in terms of PPL. The bold font represents the lowest PPL value achieved by different models, which is equivalent to the best disentanglement ability among the models. 6.5 Ablation Study
In Bi-GAE, we introduce two optimization terms: 1) T_z computed with embedded MMD-GAN, and 2) T_x based on SSIM. To evaluate the effectiveness of these added structures, we conduct evaluations on the CelebA-HQ dataset at the resolution of 256\times 256 , and compare the capabilities of representation, generation, and reconstruction of Bi-GAE with that of five control groups: 1) BiGAN: comparable to Bi-GAE without the two terms T_x and T_z ; 2) Bi-GAE- {\text{perceptual}_x} : replacing T_x with the terms of perceptual loss[21] between the data samples x and the reconstructed results G(E(x)) ; 3) Bi-GAE-no_ T_x : removing the term T_x from Bi-GAE; 4) Bi-GAE- \text{mse}_z : replacing T_z with the terms of MSE loss between the latent samples z and the re-encoded result E(G(z)) ; 5) Bi-GAE-no_ T_z : removing the term T_z from Bi-GAE. All the experiments are repeated three times, and the best results of the six Bi-GAE variants are listed.
6.5.1 Generation Performance
Table 7 lists the FID results of the six Bi-GAE variants to evaluate the generative capability. We make two observations. First, the introduction of term T_x effectively improves the generation performance (FID is reduced by about 7.12 when enabling the term T_x ). Second, Bi-GAE can achieve a similar level of generative ability when T_x is adopted based on either SSIM or perceptual loss. This is mainly because both SSIM-based and perceptual-based T_x optimize the generator by considering human visual models.
Table 7. Generation Performance of Bi-GAEs on CelebA-HQModel FID BiGAN (neither T_x nor T_z) 41.061 Bi-GAE-{\text{perceptual}_x} 31.191 Bi-GAE-no_T_x 38.338 Bi-GAE-\text{mse}_z 34.549 Bi-GAE-no_T_z 34.328 Bi-GAE (ours) {31.220} Note: 1) We use the images with the resolution of 256 \times 256 in the CelebA-HQ dataset to evaluate the generation performance of the variants of Bi-GAE in terms of FID. 2) The bold font represents the lowest FID value among the variants, which represents the best generation performance. In addition, it can be found that removing T_z or simply replacing the embedded GAN structure with the MSE loss can impair the generative power of Bi-GAE. These experimental results verify that cycle-consistency optimization using the embedded GAN in Bi-GAE improves the information expansion between z and G(z) , as proved by (8) and Theorem 1.
6.5.2 Representation Performance
Similar to Subsection 6.2, we use the encoding results of the six Bi-GAE variants as the input to the four classifiers. Table 8 lists the classification accuracy of the four classifiers to evaluate the representational capability of the encoder in Bi-GAE. We find that the average classification accuracy can be improved by about 6.75\% by introducing the MMD-based T_z to Bi-GAE. This improvement reflects that the MMD-GAN framework ( D_z ) embedded in Bi-GAE optimizes the encoder to capture more semantic-relevant features. Meanwhile, compared with MSE loss, the embedded GAN framework can improve the average classification accuracy by about 2.17\% .
Table 8. Classification Accuracy (%) of Bi-GAEs on CelebA-HQModel CelebA-HQ SVM RF AdaBoost LDA BiGAN (neither T_x nor T_z) 48.42 40.69 41.29 61.37 Bi-GAE-{\text{perceptual}_x} 52.45 48.86 45.86 60.04 Bi-GAE-no_T_x 51.70 50.50 47.39 66.12 Bi-GAE-\text{mse}_z 53.00 50.94 48.03 67.02 Bi-GAE-no_T_z 36.74 51.24 46.83 65.85 Bi-GAE (ours) 54.85 52.91 51.10 68.79 Note: 1) We use the six variants of Bi-GAE to encode the images with the resolution of 256\times 256 in the CelebA-HQ dataset. The latent results encoded by the variants are inputted to the four classifiers whose classification accuracy is used to evaluate the representation performance of the variants. 2) The bold font represents the highest classification accuracy of a classifier when inputting the latent results encoded by different variants. The highest accuracy is equivalent to the best representation performance among the variants of Bi-GAE. As proved in (8), this improvement can be explained as the MMD-based D_z with a higher order of Gaussian kernels can achieve a further reduction in the upper bound of the MMD between the data/latent space and the reconstructed data/latent space when the model is nearly convergent. This reduction can further optimize the information extension between the real latent space and the encoded latent space, which cannot be achieved by a single element-level loss (i.e., MSE).
In addition, we observe that term T_x also indirectly affects the representational power. By removing T_x or introducing the perceptual loss term, the representational capability is reduced compared with the canonical Bi-GAE. This is because that the optimization of cycle-consistency via T_z and T_x is actually a joint optimization between the encoding and decoding processes as defined in (8). For example, following Johnson et al.[21], the perceptual loss in our experiments is computed by a VGG-based perceptual loss network pre-trained on the imageNet dataset. When using the perceptual loss term in the optimization term T_x , the pre-trained feature representations are implicit in the weights of the perceptual loss network as shown in (11), which brings the unstable gradients and causes the instability of the training process of the generator as shown in Fig.4(d). Since D_z estimates the MMD between the real latent space Z and the reconstructed latent space E(G({\boldsymbol{Z}})) when training the encoder, we find that the pre-trained perceptual representation effect on T_x computation is indirectly passed to the encoder. These pre-trained feature representations can lead to performance degradation in terms of the representation of Bi-GAE due to the embedding of semantic-relevant features extracted from imageNet which is different from the features in the space of training data.
6.5.3 Overall Reconstruction Performance
Table 9 lists the reconstruction performance of the six Bi-GAE variants. We observe that the combination of the modules in Bi-GAE enables the joint optimization of the decoding and encoding processes. For example, removing T_z can alleviate the trade-off between the encoder and decoder/generator when training Bi-GAE, and enable BiGAE to achieve a higher SSIM value. However, keeping T_z can reduce the overall FID by about 2.9 because introducing T_z improves the feature representational capability. Therefore, our Bi-GAE adopts T_z and an embedded GAN structure to further improve the joint performance of the generator and encoder. In addition, Bi-GAE chooses the SSIM-based term instead of the perceptual loss. This is mainly because we aim to avoid the conflicting effect between perceptual loss and MMD-based feature representation optimization, and to achieve further joint optimization of the encoder and generator while ensuring stable convergence of Bi-GAE. Overall, by introducing T_x and T_z (embedded D_z ) to Bi-GAE, we improve the feature representational capability under the premise of generative capability, and thus the overall reconstruction performance.
Table 9. Reconstruction Performance of Bi-GAEs on CelebA-HQModel SSIM FID BiGAN (neither T_x nor T_z) 0.505 41.061 Bi-GAE-\text{perceptual}_x 0.489 35.541 Bi-GAE-no_T_x 0.522 41.159 Bi-GAE-\text{mse}_z 0.534 34.278 Bi-GAE-no_T_z 0.543 33.765 Bi-GAE (ours) \bf{0.540} \bf{30.662} Note: 1) The resolution of images in this experiment is 256 \times 256. 2) The reconstruction performance is quantified in terms of SSIM and FID, respectively. The bold font represents the highest SSIM value and the lowest FID value, respectively, which are equivalent to the best reconstruction performance among the variants. 7. Discussion
According to the above experimental results, Bi-GAE achieves consistent performance improvement in reconstruction and representation. However, the generative ability and disentanglement of Bi-GAE do not achieve a significant improvement. Since disentanglement is not equivalent to the representation, we will focus on disentanglement that affects representation in future work. In addition, we can further optimize the overall performance of Bi-GAE for high-resolution images, especially in terms of generative capability, mainly in the following three ways: 1) using a progressive training scheme to train Bi-GAE with images growing from low to high resolution, 2) leveraging state-of-the-art GAN research such as StyleGAN to implement E, {G} , and {D} , and 3) training Bi-GAE on larger datasets, such as FFHQ[8] and the whole CelebA[44], to avoid over-fitting.
8. Conclusions
In this paper, we proposed Bi-GAE to address the challenge of bidirectional joint optimization of the generator and the encoder. Meanwhile, we realized the optimization of the cycle-consistency between the real and reconstructed data/latent space for bidirectional auto-encoders. In encoding, we embedded an MMD-based GAN to enhance the feature representational capability and the convergence of Bi-GAE. In decoding, an SSIM-based is applied to guide the generator to follow human visual models. The theoretical analysis proved that our cycle-consistency optimization mechanisms enhance feature learning capabilities. We conducted extensive experiments on diverse datasets at multiple image resolutions. The experimental results confirmed that Bi-GAE improves the feature representational capability under the premise of competitive generative capability, and has stable convergence in training.
-
Figure 4. Training of Bi-GAE, Bi-GAE- {\text{perceptual}_x} , BiGAN, and BiGAN-QP on the CelebA-HQ dataset at the resoultion of 256 \times 256 . (a) Training loss curve in terms of the Wasserstein Distance. (b) Training loss curve in terms of the MMD in T_z . (c) Training loss curve in terms of the MS-SSIM in T_x . (d) Training loss curve in terms of the perceptual loss for Bi-GAE- {\text{ perceptual}_x} .
Table 1 Comparison of Existing Studies
Model Bidirectional Mapping Cycle-Consistency Optimization Realization SIT OFR Space Emb. Str. Loss WGAN[18] \times \times \times \times \times \times LSGAN[10] \times \times \times \times \times \times StyleGAN[8] \times \times \times \times \times \times CycleGAN[2] d-d \times \times Data GAN Element-level AAE[14] d-l \times \checkmark Data, latent GAN Space-level ALAE[15] d-l \times \checkmark Data, latent \times Element-level IntroVAE[30] d-l \times \checkmark Latent \times Space-level BiGAN[11] d-l \checkmark \times \times \times \times BiGAN-QP[31] d-l \checkmark \checkmark Data, latent \times Element-level Bi-GAE (ours) d-l \checkmark \checkmark Data, latent GAN Space-level Note: 1) d-d and d-l stand for the bidirectional mapping between the data space and another data space, and between the data space and the latent space respectively. 2) SIT and OFR stand for simultaneously independent training and an additional scheme for optimizing feature representation respectively. 3) Space, Emb. Str., and Loss stand for the space, the embedded structure in the framework, and the added loss term respectively for cycle-consistency optimization; ``data" and ``latent" mean making the optimization on the data and the latent space respectively; element-level and space-level mean the loss term from the direct errors between elements (e.g., MSE and MAE) and from the distribution discrepancy between the two spaces (e.g., maximum mean discrepancy (MMD), Wasserstein distance and evidence lower bound objective (ELBO)), respectively. Table 2 Parameter Settings of Bi-GAE
Resolution n_\text{b} N_{\text{GPU}} N_{\text{epoch}} s_\text{i} s_\text{l} lr_{{DF}} lr_{{EG}} lr_{D_z} \alpha_1 \alpha_2 MNIST {28\times28} 128 1 150 28 80 0.000120 0.00012 0.00008 0.6 0.840 CelebA-HQ {128\times128} 64 1 380 128 128 0.000120 0.00012 0.00009 0.7 0.750 {256\times256} 64 2 400 256 256 0.000150 0.00015 0.00012 0.8 0.720 {512\times512} 32 4 400 512 512 0.000018 0.00018 0.00014 0.8 0.675 Note: 1) This table lists the hyper-parameter settings for the experiments on the dataset MNIST[38] and CelebA-HQ[16], respectively. 2) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset in our implementation. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. Algorithm 1. Training Procedure 1: \theta_{E},\;\theta_{G},\;\theta_{{F}},\;\theta_{D},\;\theta_{D_{z}} \leftarrow \text{Initial parameters}; 2: while (not convergent){ 3: for (i=0 ; i<Iter_{D} ; i++ ){ 4: x \leftarrow n_\text{b}\text{ samples from the data space } {\boldsymbol{X}} ; 5: z \leftarrow n_\text{b}\text{ samples from the latent space } {\boldsymbol{Z}} ; 6: Compute L_{DF} ; update \theta_{\text{F}} , \theta_{D} by {Adam_{{DF}}} ; 7: } 8: x \leftarrow n_\text{b}\text{ samples from the data space } {\boldsymbol{X}} ; 9: z \leftarrow n_\text{b}\text{ samples from the latent space } {\boldsymbol{Z}} ; 10: \check{x} \leftarrow G(E_{\text{ng}}(x)) ; 11: Compute T_x , L_{{EG}} ; update \theta_{E} , \theta_{G} with {Adam_{{EG}}} ; 12: {\bf {for}} (i=0 ; i<Iter_{D_z} ; i++ ){ 13: z \leftarrow n_\text{b}\text{ samples from the latent space } {\boldsymbol{Z}} ; 14: Compute L_{D_z} ; update \theta_{D_z} with {Adam_{D_z}} ; 15: } 16: z \leftarrow n_\text{b}\text{ samples from the latent space }{\boldsymbol{Z}} ; 17: \check{z} \leftarrow E(G_\text{ng}(z)) ; 18: Compute T_z ; update \theta_E using Adam_{{EG}} with lr_{{EG}_{z}} ; 19: } Table 3 Classification Accuracy (%) on the MNIST and CelebA-HQ Datasets
Model MNIST CelebA-HQ 28\times28 128\times128 256\times256 512\times512 SVM RF AdaBoost LDA SVM RF AdaBoost LDA SVM RF AdaBoost LDA SVM RF AdaBoost LDA BiGAN {92.70} {84.83} 70.49 82.33 48.51 40.43 43.63 57.26 48.42 40.69 41.29 61.37 28.26 41.60 35.12 63.67 BiGAN-QP \bf{97.92} 93.44 85.34 91.25 54.99 41.62 40.85 52.97 52.91 38.94 38.15 54.67 30.23 34.81 31.71 48.47 AAE 96.05 {90.64} 60.83 77.39 40.63 41.12 41.92 56.12 31.22 38.88 40.31 58.41 17.34 40.76 31.14 64.12 Bi-GAE (ours) {97.18} \bf{94.09} \bf{86.99} \bf{91.55} \bf{58.73} \bf{55.09} \bf{53.65} \bf{62.19} \bf{54.85} \bf{52.91} \bf{51.10} \bf{68.79} \bf{48.75} \bf{43.72} \bf{42.10} \bf{66.42} Note: 1) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset in our experiments. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. 2) This table lists the accuracy of four classifiers, i.e., SVM, RF, AdaBoost, and LDA when inputting the encoding results of the MNIST and CelebA-HQ datasets. These encoding results are computed by the four different AE models. 3) The bold font represents the highest classification accuracy of a classifier, which is equivalent to the best representation performance among the AE models. Table 4 Generation Performance in Terms of FID Metric on the MNIST and CelebA-HQ Datasets
Model Type FID MNIST CelebA-HQ 28\times 28 128\times128 256\times256 512\times512 BiGAN AE 6.779 {31.580} 41.058 49.002 BiGAN-QP AE 12.290 39.338 57.443 68.371 AAE AE 41.823 44.297 59.189 76.721 Bi-GAE (ours) AE 5.736 26.162 31.223 44.031 WGAN GAN - 20.736 25.473 28.831 Note: 1) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. 2) The generation performance is measured in terms of FID in this table. The bold font represents the lowest FID value of the images generated by different models on the dataset with a specific resolution, which is equivalent to the best generation performance among the models. 3) AE and GA stand for the auto-encoders and the GAN-based generators, which are diverse types of generative models. Table 5 Reconstruction Performance in Terms of SSIM and FID on the MNIST and CelebA-HQ Datasets
Model SSIM FID MNIST CelebA-HQ MNIST CelebA-HQ 28\times 28 128\times128 256\times256 512\times512 28\times 28 128\times128 256\times256 512\times512 BiGAN 0.767 0.501 0.505 0.490 8.157 30.750 41.061 47.605 BiGAN-QP 0.782 0.489 0.449 0.396 10.437 38.642 55.353 70.319 AAE 0.926 0.509 0.523 0.512 8.013 40.301 57.472 73.773 Bi-GAE (ours) 0.771 0.504 0.540 0.535 8.416 {25.420} 30.621 45.125 Note: 1) 128\times 128, 256 \times 256, and 512 \times 512 stand for different resolutions of images in the CelebA-HQ dataset in our experiments. Similarly, 28\times 28 stands for the resolution of images in the MNIST dataset. 2) The reconstruction performance is quantified in terms of SSIM and FID, respectively. The bold font represents the highest SSIM value and the lowest FID value respectively. The highest SSIM value and the lowest FID value are equivalent to the best reconstruction performance among the models, respectively. Table 6 Disentanglement Ability on CelebA-HQ
Model PPL Full End BiGAN 13.868 {4.735} BiGAN-QP 3.598 3.031 AAE 14.756 6.751 Bi-GAE (ours) {11.368} 5.245 Note: 1) We use the images in the CelebA-HQ dataset at the resolution of 256 \times 256 to evaluate the disentanglement ability of different models. 2) The disentanglement ability is quantified in terms of PPL. The bold font represents the lowest PPL value achieved by different models, which is equivalent to the best disentanglement ability among the models. Table 7 Generation Performance of Bi-GAEs on CelebA-HQ
Model FID BiGAN (neither T_x nor T_z) 41.061 Bi-GAE-{\text{perceptual}_x} 31.191 Bi-GAE-no_T_x 38.338 Bi-GAE-\text{mse}_z 34.549 Bi-GAE-no_T_z 34.328 Bi-GAE (ours) {31.220} Note: 1) We use the images with the resolution of 256 \times 256 in the CelebA-HQ dataset to evaluate the generation performance of the variants of Bi-GAE in terms of FID. 2) The bold font represents the lowest FID value among the variants, which represents the best generation performance. Table 8 Classification Accuracy (%) of Bi-GAEs on CelebA-HQ
Model CelebA-HQ SVM RF AdaBoost LDA BiGAN (neither T_x nor T_z) 48.42 40.69 41.29 61.37 Bi-GAE-{\text{perceptual}_x} 52.45 48.86 45.86 60.04 Bi-GAE-no_T_x 51.70 50.50 47.39 66.12 Bi-GAE-\text{mse}_z 53.00 50.94 48.03 67.02 Bi-GAE-no_T_z 36.74 51.24 46.83 65.85 Bi-GAE (ours) 54.85 52.91 51.10 68.79 Note: 1) We use the six variants of Bi-GAE to encode the images with the resolution of 256\times 256 in the CelebA-HQ dataset. The latent results encoded by the variants are inputted to the four classifiers whose classification accuracy is used to evaluate the representation performance of the variants. 2) The bold font represents the highest classification accuracy of a classifier when inputting the latent results encoded by different variants. The highest accuracy is equivalent to the best representation performance among the variants of Bi-GAE. Table 9 Reconstruction Performance of Bi-GAEs on CelebA-HQ
Model SSIM FID BiGAN (neither T_x nor T_z) 0.505 41.061 Bi-GAE-\text{perceptual}_x 0.489 35.541 Bi-GAE-no_T_x 0.522 41.159 Bi-GAE-\text{mse}_z 0.534 34.278 Bi-GAE-no_T_z 0.543 33.765 Bi-GAE (ours) \bf{0.540} \bf{30.662} Note: 1) The resolution of images in this experiment is 256 \times 256. 2) The reconstruction performance is quantified in terms of SSIM and FID, respectively. The bold font represents the highest SSIM value and the lowest FID value, respectively, which are equivalent to the best reconstruction performance among the variants. -
[1] Liu W B, Wang Z D, Liu X H, Zeng N Y, Liu Y R, Alsaadi F E. A survey of deep neural network architectures and their applications. Neurocomputing, 2017, 234: 11–26. DOI: 10.1016/j.neucom.2016.12.038.
[2] Zhu J Y, Park T, Isola P, Efros A A. Unpaired image-to-image translation using cycle-consistent adversarial networks. In Proc. the 2017 IEEE International Conference on Computer Vision (ICCV), Oct. 2017, pp.2242–2251. DOI: 10.1109/ICCV.2017.244.
[3] Tewari A, Zollhöfer M, Kim H, Garrido P, Bernard F, Pérez P, Theobalt C. MoFA: Model-based deep convolutional face autoencoder for unsupervised monocular reconstruction. In Proc. the 2017 IEEE International Conference on Computer Vision (ICCV), Oct. 2017, pp.3735–3744. DOI: 10.1109/ICCV.2017.401.
[4] Li X P, She J. Collaborative variational autoencoder for recommender systems. In Proc. the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2017, pp.305–314. DOI: 10.1145/3097983.3098077.
[5] Zhou C, Paffenroth R C. Anomaly detection with robust deep autoencoders. In Proc. the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Aug. 2017, pp.665–674. DOI: 10.1145/3097983.3098052.
[6] Doersch C. Tutorial on variational autoencoders. arXiv: 1606.05908, 2016. https://doi.org/10.48550/arXiv.1606.05908, May 2023.
[7] Creswell A, White T, Dumoulin V, Arulkumaran K, Sengupta B, Bharath A A. Generative adversarial networks: An overview. IEEE Signal Processing Magazine, 2018, 35(1): 53–65. DOI: 10.1109/MSP.2017.2765202.
[8] Karras T, Laine S, Aila T. A style-based generator architecture for generative adversarial networks. IEEE Trans. Pattern Analysis and Machine Intelligence, 2021, 43(12): 4217–4228. DOI: 10.1109/TPAMI.2020.2970919.
[9] Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, Courville A. Improved training of Wasserstein GANs. In Proc. the 31st International Conference on Neural Information Processing Systems, Dec. 2017, pp.5769–5779. DOI: 10.5555/3295222.3295327.
[10] Mao X D, Li Q, Xie H R, Lau R Y K, Wang Z, Smolley S P. Least squares generative adversarial networks. In Proc. the 2017 IEEE International Conference on Computer Vision (ICCV), Oct. 2017, pp.2813–2821. DOI: 10.1109/ICCV.2017.304.
[11] Donahue J, Krähenbühl P, Darrell T. Adversarial feature learning. arXiv: 1605.09782, 2016. https://doi.org/10.48550/arXiv.1605.09782, May 2023.
[12] Radford A, Metz L, Chintala S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv: 1511.06434, 2015. https://doi.org/10.48550/arXiv.1511.06434, May 2023.
[13] Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I, Abbeel P. InfoGAN: Interpretable representation learning by information maximizing generative adversarial nets. In Proc. the 30th International Conference on Neural Information Processing Systems, Dec. 2016, pp.2180–2188. DOI: 10.5555/3157096.3157340.
[14] Makhzani A, Shlens J, Jaitly N, Goodfellow I, Frey B. Adversarial autoencoders. arXiv: 1511.05644, 2015. https://doi.org/10.48550/arXiv.1511.05644, May 2023.
[15] Pidhorskyi S, Adjeroh D A, Doretto G. Adversarial latent autoencoders. In Proc. the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2020, pp.14092–14101. DOI: 10.1109/CVPR42600.2020.01411.
[16] Karras T, Aila T, Laine S, Lehtinen J. Progressive growing of GANs for improved quality, stability, and variation. arXiv: 1710.10196, 2017. https://doi.org/10.48550/arXiv.1710.10196, May 2023.
[17] Li C L, Chang W C, Cheng Y, Yang Y M, Póczos B. MMD GAN: Towards deeper understanding of moment matching network. In Proc. the 31st International Conference on Neural Information Processing Systems, Dec. 2017, pp.2200-2210.
[18] Arjovsky M, Chintala S, Bottou L. Wasserstein generative adversarial networks. In Proc. the 34th International Conference on Machine Learning, Aug. 2017, pp.214-223. DOI: 10.5555/3305381.3305404.
[19] Wang Z W, She Q, Ward T E. Generative adversarial networks in computer vision: A survey and taxonomy. ACM Computing Surveys, 2021, 54(2): Article No. 37. DOI: 10.1145/3439723.
[20] Pan Z Q, Yu W J, Yi X K, Khan A, Yuan F, Zheng Y H. Recent progress on generative adversarial networks (GANs): A survey. IEEE Access, 2019, 7: 36322–36333. DOI: 10.1109/ACCESS.2019.2905015.
[21] Johnson J, Alahi A, Li F F. Perceptual losses for real-time style transfer and super-resolution. In Proc. the 14th European Conference on Computer Vision, Oct. 2016, pp.694–711. DOI: 10.1007/978-3-319-46475-6_43.
[22] Berthelot D, Schumm T, Metz L. BEGAN: Boundary equilibrium generative adversarial networks. arXiv: 1703.10717, 2017. https://doi.org/10.48550/arXiv.1703.10717, May 2023.
[23] Wang T C, Liu M Y, Zhu J Y, Tao A, Kautz J, Catanzaro B. High-resolution image synthesis and semantic manipulation with conditional GANs. In Proc. the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Jun. 2018, pp.8798–8807. DOI: 10.1109/CVPR.2018.00917.
[24] Zhang H, Xu T, Li H S, Zhang S T, Wang X G, Huang X L, Metaxas D. StackGAN: Text to photo-realistic image synthesis with stacked generative adversarial networks. In Proc. the 2017 IEEE International Conference on Computer Vision, Oct. 2017, pp.5908–5916. DOI: 10.1109/ICCV.2017.629.
[25] Karras T, Laine S, Aittala M, Hellsten J, Lehtinen J, Aila T. Analyzing and improving the image quality of StyleGAN. In Proc. the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2020, pp.8107–8116. DOI: 10.1109/CVPR42600.2020.00813.
[26] Rezende D J, Mohamed S, Wierstra D. Stochastic backpropagation and approximate inference in deep generative models. In Proc. the 31st International Conference on International Conference on Machine Learning, Jun. 2014, pp.1278–1286. DOI: 10.5555/3044805.3045035.
[27] Chen R T Q, Li X C, Grosse R, Duvenaud D. Isolating sources of disentanglement in VAEs. In Proc. the 32nd International Conference on Neural Information Processing Systems, Dec. 2018, pp.2615–2625. DOI:10.5555/3327144.3327186.
[28] Roy A, Grangier D. Unsupervised paraphrasing without translation. arXiv: 1905.12752, 2019. https://doi.org/10.48550/arXiv.1905.12752, May 2023.
[29] Kingma D P, Salimans T, Jozefowicz R, Chen X, Sutskever I, Welling M. Improved variational inference with inverse autoregressive flow. In Proc. the 30th International Conference on Neural Information Processing Systems (NIPS), Dec. 2016, pp.4743–4751. DOI: 10.5555/3157382.3157627.
[30] Huang H B, Li Z H, He R, Sun Z N, Tan T N. IntroVAE: Introspective variational autoencoders for photographic image synthesis. In Proc. the 32nd International Conference on Neural Information Processing Systems, Dec. 2018, pp.52–63. DOI: 10.5555/3326943.3326949.
[31] Su J L. GAN-QP: A novel GAN framework without gradient vanishing and lipschitz constraint. arXiv: 1811.07296, 2018. https://doi.org/10.48550/arXiv.1811.07296, May 2023.
[32] Arora S, Ge R, Liang Y Y, Ma T Y, Zhang Y. Generalization and equilibrium in generative adversarial nets (GANs). In Proc. the 34th International Conference on Machine Learning, Aug. 2017, pp.224–232. DOI: 10.1145/3188745.3232194.
[33] Wang W, Sun Y, Halgamuge S. Improving MMD-GAN training with repulsive loss function. arXiv: 1812.09916, 2018. https://doi.org/10.48550/arXiv.1812.09916, May 2023.
[34] Gatys L A, Ecker A S, Bethge M. Image style transfer using convolutional neural networks. In Proc. the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2016, pp.2414–2423. DOI: 10.1109/CVPR.2016.265.
[35] Liu Y F, Chen H, Chen Y, Yin W, Shen C H. Generic perceptual loss for modeling structured output dependencies. In Proc. the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Jun. 2021, pp.5420–5428. DOI: 10.1109/CVPR46437.2021.00538.
[36] He K M, Zhang X Y, Ren S Q, Sun J. Delving deep into rectifiers: Surpassing human-level performance on imageNet classification. In Proc. the 2015 IEEE International Conference on Computer Vision (ICCV), Dec. 2015, pp.1026–1034. DOI: 10.1109/ICCV.2015.123.
[37] Zhao H, Gallo O, Frosio I, Kautz J. Loss functions for image restoration with neural networks. IEEE Trans. Computational Imaging, 2017, 3(1): 47–57. DOI: 10.1109/TCI.2016.2644865.
[38] Deng L. The MNIST database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Processing Magazine, 2012, 29(6): 141–142. DOI: 10.1109/MSP.2012.2211477.
[39] Hearst M A, Dumais S T, Osuna E, Platt J, Scholkopf B. Support vector machines. IEEE Intelligent Systems and their Applications, 1998, 13(4): 18–28. DOI: 10.1109/5254.708428.
[40] Ye J P. Least squares linear discriminant analysis. In Proc. the 24th International Conference on Machine Learning, Jun. 2007, pp.1087–1093. DOI: 10.1145/1273496.1273633.
[41] Rigatti S J. Random forest. Journal of Insurance Medicine, 2017, 47(1): 31–39. DOI: 10.17849/insm-47-01-31-39.1.
[42] Hastie T, Rosset S, Zhu J, Zou H. Multi-class AdaBoost. Statistics and Its Interface, 2009, 2(3): 349–360. DOI: 10.4310/SII.2009.v2.n3.a8.
[43] Zhang H, Goodfellow I, Metaxas D, Odena A. Self-attention generative adversarial networks. arXiv: 1805.08318, 2018. https://doi.org/10.48550/arXiv.1805.08318, May 2023.
[44] Liu Z W, Luo P, Wang X G, Tang X O. Deep learning face attributes in the wild. In Proc. the 2015 IEEE International Conference on Computer Vision (ICCV), Dec. 2015, pp.3730–3738. DOI: 10.1109/ICCV.2015.425.
-
期刊类型引用(1)
1. Haoran Lu, Lei Wang, Xiaoliang Ma, et al. A survey of graph neural networks and their industrial applications. Neurocomputing, 2024.  必应学术
必应学术
其他类型引用(0)
-
其他相关附件
-
本文中文pdf
2023-3-12-1902-Chinese Information 点击下载(28KB) -
本文英文pdf
2023-3-12-1902-Highlights 点击下载(159KB) -
本文附件外链
https://rdcu.be/djH6X
-




 下载:
下载: