1.   Introduction

Nowadays, a massive amount of data is generated by mobile users, Internet of Things (IoT) devices and artificial intelligence applications, providing potential training datasets for diverse machine learning (ML) tasks. Traditionally, one needs to upload the whole dataset to the remote cloud center for centralized machine learning model training. However, it is non-trivial to upload a large amount of data to the remote data center due to the limited network bandwidth and data privacy concerns. Since training data is generated at the network edge, such as from smart sensing devices and smartphones connected to the edge, edge computing coupled with distributed machine learning is a natural alternative. Nevertheless, training ML models in the edge cloud still faces many challenges. First, due to limited data and computing resources, a single edge device/server may not be able to perform a high-quality ML training task alone. Second, the computing capacity and network resources of edge devices/servers are limited and heterogeneous. When performing ML training tasks, different edge units may lead to various convergence speeds and performances. Third, edge resources generally are shared by many mobile users. Distributed ML training within the edge cloud has to be constrained by the shared resources and the resource competition among various users, servers, and applications.

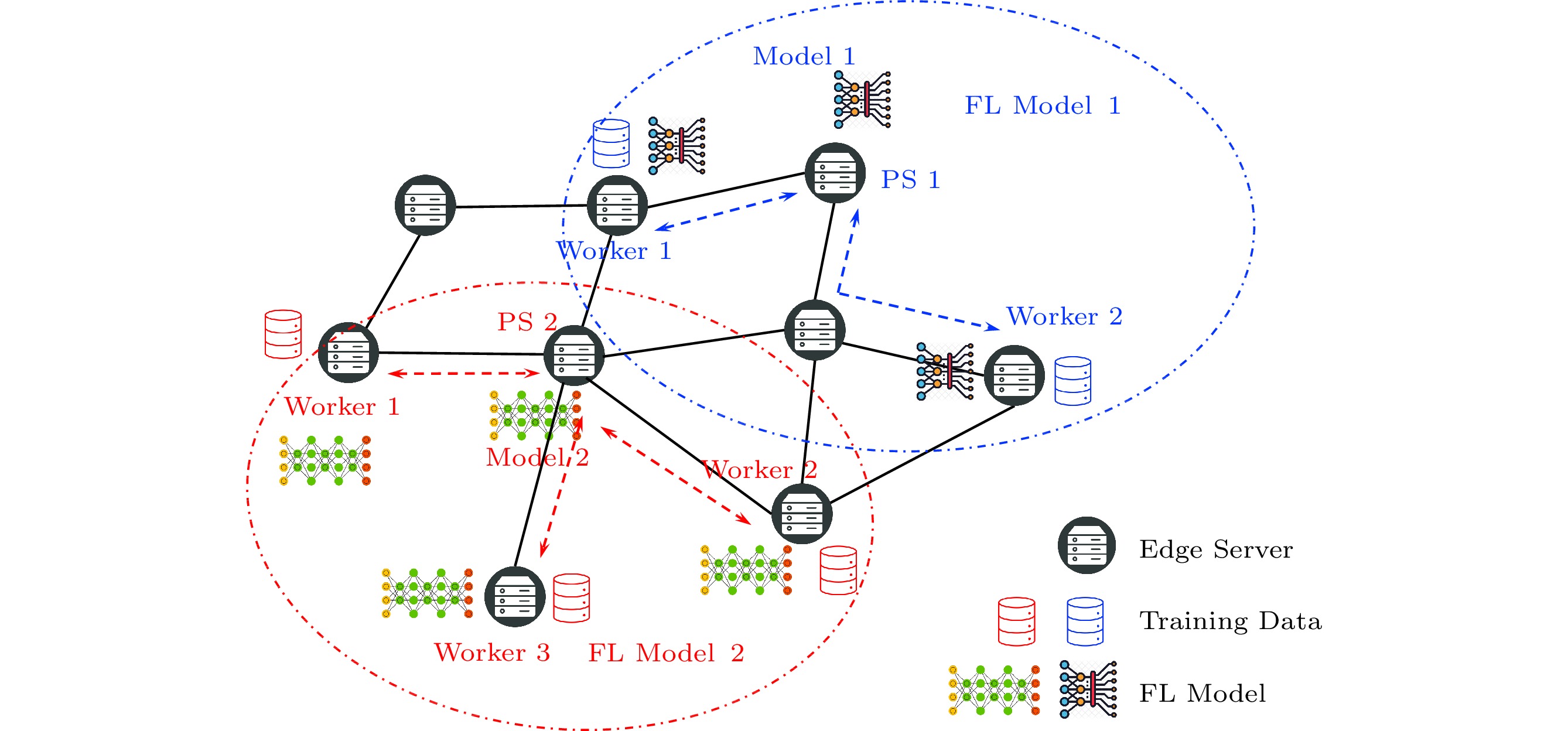
To tackle the aforementioned challenges, a new distributed machine learning paradigm has been proposed, called federated learning (FL)^[1–3] that conducts distributed learning at multiple clients without sharing raw local data among themselves. Coupled with edge computing, FL over edge cloud has been recently studied in various settings^[4–14]. In such scenarios, several edge servers have been selected as participants (either parameter servers or FL workers), and collaboratively train a shared global ML model without sharing their local datasets and decoupling the ability to do model training from the need to store data in a centralized server. More precisely, as shown in Fig.1, in each global iteration, edge servers, worked as workers, first download the latest global model from the parameter server (PS), and then perform a fixed number of rounds of local training based on their local data. After that, edge servers will upload their local models to the parameter server which is responsible for aggregating parameters from different workers and sending the aggregated global model back to each FL worker. Previously, the efforts of FL over the edge have been focused on the convergence and adaptive control^{[5, 6]}, the resource allocation and model aggregation^{[8, 10, 11]}, and the communication and energy efficiency^{[1, 16, 17]}.

Figure  1.  Example of multi-model FL over the edge: two FL models are trained with three and four participants (1 PS + 2 or 3 FL workers), respectively, in a shared edge cloud^[15].

下载: 全尺寸图片 幻灯片

In this work, we focus on a joint participant selection and learning optimization problem in multi-model FL over a shared edge cloud ¹. For each FL model, we aim to find one PS and multiple FL workers and decide the local convergence rate for FL workers. Note that both worker selection and learning rate control have been studied in FL recently. For example, Nishio et al.^[7] studied a client selection problem in decentralized edge learning where a set of mobile clients are chosen to act as workers for FL and their aim is to maximize the selected clients under time constraints. Jin et al.^[9] also studied the joint control of local learning rate and edge provisioning in FL to minimize the long-term cumulative cost. However, all of these studies focus on the optimization of training one global FL model instead of multiple FL models, thus they do not consider the parameter server selection for different FL models and ignore the competition of resources among different FL models. In the real scenario, there might be multiple FL models training simultaneously in the edge cloud (Fig.1 shows an example where two FL models are trained with three and four participants, respectively). Especially in the edge computing environment, edge servers can store different types of data and serve different FL models or tasks for diverse applications. With heterogeneous resources and capacities at edge devices, when multiple FL models are trained at the same time, which FL model is preferentially served at which edge server directly affects the total communication cost and computational cost of the FL training. The selection of participants (both the PS and FL workers) for each model will also affect the learning convergence speed. Therefore, in this paper, we formulate a new joint optimization problem of participant selection and learning rate scheduling of multi-model FL, where multiple FL models are trained concurrently in an edge cloud.

Due to the limitation of shared computing and networking resources at edge servers in the edge cloud, we aim to carefully select the FL participants for each FL model and pick the appropriate local learning rate for these selected FL workers, so as to minimize the total cost of FL training of all models while meeting the convergence requirement from each model. The main contributions of this work are summarized as follows.

1) We formulate a new joint participant selection and learning rate scheduling problem of multi-model federated learning in an edge cloud as a mixed-integer programming problem, with a goal to minimize the total FL cost while satisfying various constraints. Note that by allowing different FL models to pick their own PS, it can better handle the competition among models and provide load balancing in the edge cloud compared with the traditional FL solution with a centralized PS for all models.

2) We decouple the original optimization problem into two or three sub-problems and then propose three algorithms to effectively find participants and the learning rate for each FL model, by iteratively solving the sub-problems. We further consider the impact of the processing order of FL models in a resource-limited and heterogeneous edge scenario.

3) We conduct extensive simulations with real FL tasks to evaluate our proposed algorithms, and our results confirm the proposed algorithms can effectively reduce the total FL cost compared with the existing work^{[9, 23, 24]}.

The rest of the paper is organized as follows. Section 2 presents the overview of related work. Section 3 introduces the system model and the preliminaries of federated edge learning. Section 4 describes the problem formulation of new joint optimization, and Section 5 provides our proposed multi-stage optimization algorithms. Evaluation of our proposed algorithms is provided in Section 6. Section 7 finally concludes this paper. A preliminary version of this paper appears as [15], and this version includes newly introduced greedy-based variation using a different model processing order, time complexity analysis, additional sets of experiment results, more comprehensive related work, and better overall presentation.

2.   Related Work

In this section, we briefly review recent studies on federated learning over edge systems^[4]. Federated learning^[5–14] has been emerging as a new distributed ML paradigm over different edge systems. Current FL frameworks can be categorized into three types based on the learning topology used for model aggregation: centralized FL (CFL), hierarchical FL (HFL), and decentralized FL (DFL). CFL is the classical FL^[9] where the parameter server (PS) and several workers form a star architecture as shown in Fig.1^[15]. Wang et al.^[6] analyzed the convergence of CFL in a constrained edge computing system and proposed a control algorithm that determines the best trade-off between local update and global parameter aggregation to minimize the loss function. This work focused on the convergence and adaptive control of FL and did not consider participant selection.

Nishio and Yonetani^[7] studied a client selection problem in CFL in mobile edge computing. Their method uses an edge server in the cellular network as the PS and selects a set of mobile clients as workers. Their client selection aims to maximize the selected workers while meeting the time constraints. Jin et al.^[9] considered a joint control of FL and the edge provisioning problem in distributed cloud-edge networks where the cloud server is the PS and active edge servers are workers. Their method controls the status of edge servers for training to minimize the long-term cumulative cost of FL and also satisfies the convergence of the trained model. Li et al.^[25] also considered client scheduling in FL to overcome client uncertainties or stragglers via learning-based task replication. While these studies are similar to ours, they focus on the optimization of one global FL model instead of multiple FL models. More importantly, these studies do not consider PS selection for multiple FL models.

Recently, Nguyen et al.^[14] studied resource sharing among multiple FL services/models in edge computing where the user equipment is used as an FL worker, and proposed a solution to optimally manage the resource allocation and learning parameter control while ensuring energy consumption requirements. However, their FL framework is different from ours. First, they used the user equipment as FL workers, while we use edge servers as FL workers. Second, they did not consider the PS selection, since they used a single edge server as the PS. Third, their model allows training multiple FL models at the same user equipment (while we do not allow the edge server to act as workers for multiple models in the same time unit), and thus their method has to manage the CPU and bandwidth allocation on the user equipment.

Both [5] and [8] consider a client-edge-cloud hierarchical federated learning (HFL) where cloud and edge servers work as two-tier parameter servers to aggregate the partial models from mobile clients (i.e., FL workers). Liu et al.^[5] proved the convergence of such an HFL, while Luo et al.^[8] also studied a joint resource allocation and edge association problem for device users under such an HFL framework to achieve global cost minimization. Wang et al.^[11] considered the cluster structure formation in HFL where edge servers are clustered for model aggregation. Recently, Wei et al.^[12] also studied the participant selection for HFL in edge clouds to minimize the learning cost. Liu et al.^[13] studied the group formation and sampling in a group-based HFL. However, our FL framework does not use HFL.

Meng et al.^[10] focused on model training of DFL using decentralized P2P methods in edge computing. While their method also selects FL workers from an edge network, the model aggregation is performed at edge devices based on a dynamically formatted P2P topology (without PS). Therefore, it is different from our studied problem, which mainly focuses on CFL.

There are also other studies^{[16, 17, 26]} where energy efficiency and/or wireless communication have/has been taken into consideration in FL in edge systems.

3.   Federated Learning over Edge Cloud

In this section, we introduce our model of edge cloud, and then describe the procedures and associated costs of federated learning over the edge cloud.

3.1   Edge Cloud Model

We model the edge cloud as a graph $G(V,E)$, consisting of $N$ edge servers and $L$ direct links among them, as shown in Fig.2. Here $V=\{v_1,\dots,v_N\}$ and $E=\{e_1,\dots,e_L\}$ are the set of edge servers and the set of links, respectively. For each edge server $v_i \in V$, it has a storage capacity $c^t_i$ and a CPU frequency $f^t_i$ at time $t$. For each edge link $e_j \in E$, it has a network bandwidth $b^t_{j}$ at time $t$. We omit $t$ from the above notations when it is clear from the context.

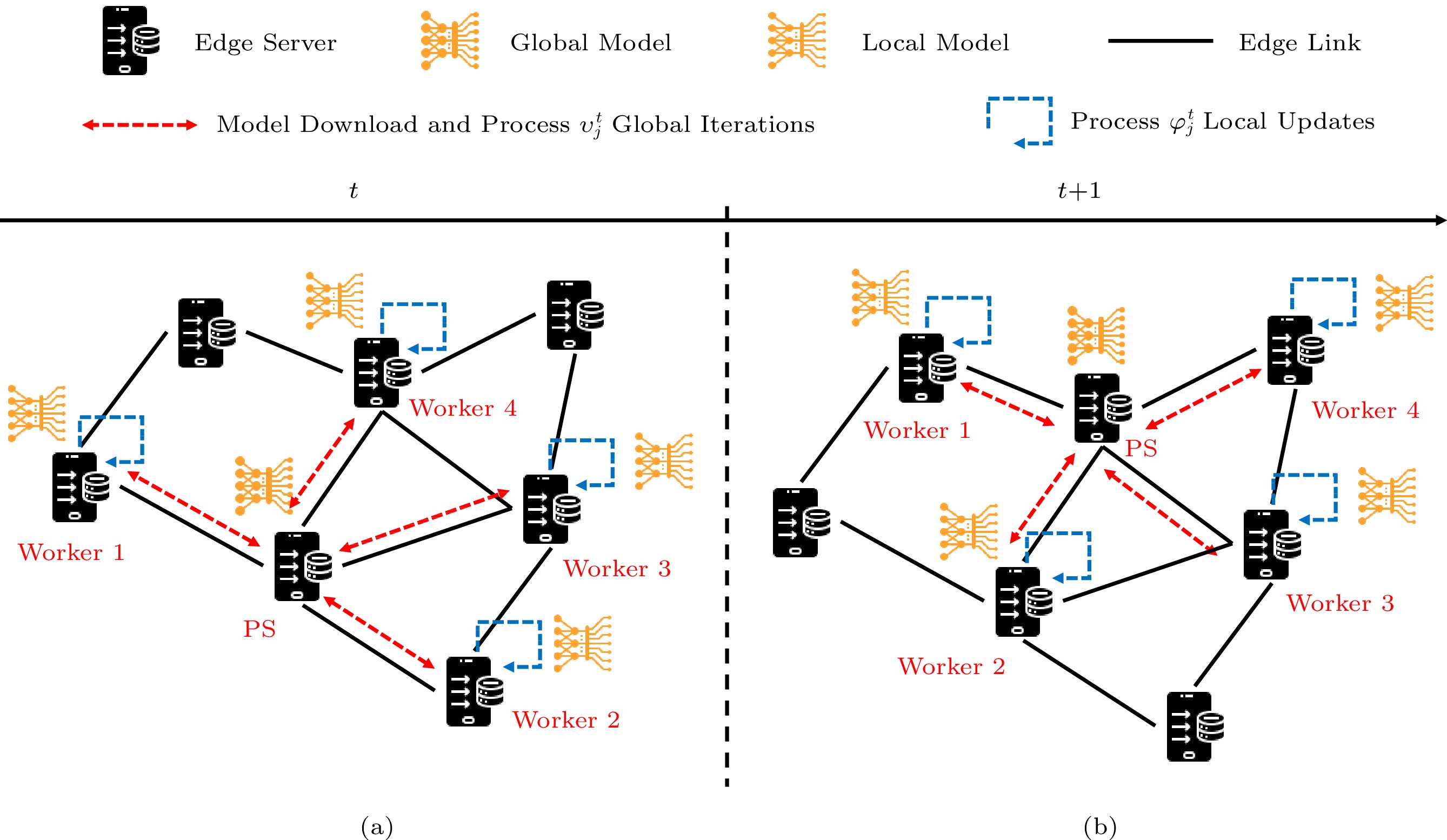
Figure  2.  Training process of an FL model within the edge network at different time periods. (a) At each time period, this FL model needs to select one PS and four workers, and they perform the FL via multiple iterations of local and global updates. (b) Due to the dynamic edge cloud environment, the model can change its participants (both PS and workers) at the next time period $t+1$ to minimize the total training cost of all models.

下载: 全尺寸图片 幻灯片

Each edge server holds a certain distinct dataset collected from mobile devices/users and can be used for local model training. We consider $O$ types of datasets in the edge cloud, and use $z_{i,k} \in \{0,1\}$ to indicate whether server $v_i$ stores the $k$-th type of datasets and $S_{i,k}$ to represent the raw sample data of the $k$-th type stored at server $v_i$. Note that one edge server can hold multiple types of datasets.

3.2   Federated Learning over Edge

We consider parallel federated learning where multiple machine learning models are trained in parallel within the edge cloud. Compared with the classical FL scenario where the remote cloud works as the parameter server (PS), we select a group of edge servers with enough capacity as the participants (one PS and multiple workers) of FL for each model. We assume that $W$ FL models ($M=\{m_1,\dots,m_W\}$) need to be trained at the same time. For the training task of each FL model $m_j$, it requests 1) $\kappa_j+1$ edge servers as participants, one server as its PS and $\kappa_j$ servers as its workers, whose CPU frequency should be larger than its required minimal CPU frequency $\chi_j$; 2) the selected workers must have the requested types of a dataset for $m_j$, where $w_{j,k} \in \{0,1\}$ indicates whether $m_j$ needs the $k$-th type of datasets; and 3) the achieved global convergence rate needs to be larger than $\varsigma_j$. Here, we assume that each model uses a fixed number of workers, and one worker can only perform the FL training of one model at a time.

We consider a series of consecutive time periods $t = 1,\dots, T$, and each time period has an equal duration $\tau$. As shown in Fig.2, at each time $t$, we select the FL participants for each model and then train $W$ models in parallel through FL, which consists of a number of global iterations (let $\vartheta_j^t$ be the number of global iterations of $m_j$ at $t$). For each model $m_j$, each global iteration includes four parts: 1) the selected parameter server initializes the global model of $m_j$; 2) the selected workers download the global model from the parameter server; 3) each worker runs the local updates using its holding raw dataset for $\varphi_j^t$ local iterations to achieve the desired local convergence rate $\varrho_j^t$; 4) workers upload the updated model and related gradient to the parameter server for the aggregation to upload the global model. The training process of federated learning at different time periods is shown in Fig.2. Table 1 summarizes all notations we used in this paper.

Table  1.  Summary of Notations

Symbol	Notation
$N$, $L$, $O$, $W$	Number of edge servers, edge links, datasets, and FL models respectively
$v_i$, $e_j$	The $i$-th edge server, and the $j$-th edge link respectively
$c_i^t$, $f_i^t$, $b_j^t$	Storage capacity of $v_i$, CPU frequency of $v_i$ , and the link bandwidth of link $e_j$ at $t$ respectively
$S_{i,k}$, $z_{i,k}$	The $k$-th type data at $v_i$, and its indicator respectively
$t , \tau,T$	Index, duration, and number of time periods respectively
$m_j$, $\kappa_j$, $\mu_j$, $\chi_j$	The $j$-th FL model, its required number of workers, model size, and CPU requirement respectively
$\varsigma_j$	Global convergence requirement of $m_j$
$w_{j,k}$, $\eta_j$	Indicator of the $k$-th type data, and the downloading cost of $m_j$ respectively
$x_{i,j}^t$, $y_{i,j}^t$	PS and FL worker selection of $e_i$ for $m_j$ respectively
$\varrho_j^t$	Local convergence rates of $m_j$ at the $t$-th time period
$\vartheta_j^t$, $\varphi_j^t$	Number of global iterations, and local update of $m_j$ at the $t$-th time period respectively
$\alpha$, $\beta$, $\delta$	Index of global iteration, local update, and step size of local update respectively
$\lambda$, $\gamma$	Parameters of loss function
$D_{j,i}^t$, $\psi(D_{j,i}^t)$	Sample data for $m_j$ at sever $v_i$ at $t$, and CPU cycles to process sample data of $D_{j,i}^t$ respectively
$\rho_j(v_{i}, v_k)$, $P_{i,k}^t$	Communication cost of $m_j$ from $v_{i}$ to $v_k$, and the shortest path from $v_i$ to $v_k$ at the t-th time period respectively
$v_{ps}^t(m_j)$	Selected PS of $m_j$ at the t-th time period
$C_{j}^{{\rm comm},t}$, $C_{j}^{{\rm init},t}$, $C_{j}^{{\rm local},t}$, $C_{j}^{{\rm global},t}$	Communication cost, initialization cost, local update cost, and global aggregation cost of $m_j$ respectively
$\varpi_{j}^{t}$	Total FL cost of $m_j$

下载: 导出CSV 

| 显示表格

Next, we define our local training and global aggregation process as well as the loss function during the federated edge learning at each time period.

Loss Function. Let all types of sample data used by the $j$-th model and stored in edge server $v_i$ be defined by $D_{j,i}^t = \bigcup_{w_{j,k}o_{i,k}=1} S_{i,k}$. For each sample data $d=< q_d, r_d > \in D_{j,i}^t$, where $q_d$ is the input data and $r_d$ is the output data/label, we define the average loss of data for the $j$-th FL model on server $v_i$ in time period $t$ as ${\cal{A}}_{j, i}^{t}(p)$:

where ${\cal{H}}(\cdotp)$ is the loss function to measure the performance of the training model ${\cal{I}}(\cdotp)$, and $p$ is the model parameter.

Then the average loss of data for the $j$-th FL model on all related edge servers in the t-th time period is defined as follows:

where $D^t_j$ is the union of all involved training samples of model $j$ at time $t$.

Local Training on FL Workers. For each global iteration of the $j$-th FL model $\alpha \in [1, \vartheta_j^t]$, the related edge server $v_i$ (FL worker) will perform the following local update process:

where $p_{j,i}^{t,\alpha}$ is the local model parameter on edge server $v_i$ in the current iteration and $p_{j}^{t,\alpha-1}$ is the aggregated model downloaded from the parameter server in the last iteration. And $p_{j}^{t,0} = p_{j}^{t-1, \vartheta_j^{t}}$. $\omega_{j,i}^{t,\alpha}$ is the local update from a gradient-based method, and it can be calculated as follows.

where $\omega_{j,i}^{t,\alpha, \beta}$ is the model parameter for the $j$-th FL model in the $\beta$-th local update and $\delta$ is the step size of the local update. Lastly, ${\cal{L}}_{j,i}^{t,\alpha}(\cdotp)$ is the predefined local update function. Based on [27], ${\cal{L}}_{j,i}^{t,\alpha}(\cdotp)$ is defined as below.

where $\xi_{1}$ and $\xi_{2}$ are two constant variables. ${\cal{J}}_{j}^{t}(\cdotp)$ is the sum of gradients among all related edge servers and this process will be performed in the global aggregation step.

Assume that ${\cal{A}}_{j,i}^{t}(\cdotp)$ is $\lambda$-Lipschitz continuous and $\gamma$-strongly convex^{[16, 28]}, then the local convergence of the local model is represented as

where ${\cal{L}}_{j,i}^{t,*}$ is the local optimum of the training model. Furthermore, we can set $\omega_{j,i}^{t, 0} = 0$ since the initial value can start from $0$ for the training model.

Global Aggregation on Parameter Server. After the local updates for all related FL workers, they have to upload the related local model parameter $\omega_{j,i}^{t,\alpha}$ and the related gradients $\nabla{\cal{A}}_{j,i}^{t}(p_{j}^{t,\alpha})$ to the parameter server for aggregation.

Then, the global average loss of data for the $j$-th model is

Similarly, the global convergence of the global model is defined as

where ${\cal{G}}_{j}^{t,*}$ is the global optimum of the training model.

Finally, from (1) and (2), in order to achieve the desired local convergence rate $\varrho_j^t$ and global convergence rate $\varsigma_j$, we need to calculate the number of local updates $\varphi_j^t$ and the number of global iterations $\vartheta_j^t$. From the above observation, we can find that the global convergence rate $\varsigma_j$ for each FL model can be predefined and we have to conduct the local update and global iteration to achieve required global convergence rate. Then we have the following relationship between the convergence rate and the local update as well as global iterations^{[9, 27]}.

where $\xi_1$ is the constant variable defined in function ${\cal{L}}_{j,i}^{t,\alpha}(\cdotp)$, $\lambda$ is the $\lambda$-Lipschitz parameter, and $\gamma$ is the $\gamma$-strongly convex parameter. Both the values of $\lambda$ and $\gamma$ are determined by the loss function. $\vartheta_0$ and $\varphi_0$ are two constants where $\vartheta_0 = {2\lambda^2}/({\gamma^2 \xi_1})$ and $\varphi_0 = {2}/({(2-\lambda\delta)\delta\gamma})$.

4.   Problem: Joint Participant Selection and Learning Optimization

In this section, we first formulate the studied joint optimization problem, and then introduce the cost models used there.

4.1   Problem Formulation

Under the previously introduced multi-model federated learning scenario, we consider how to choose participants for each of the models and how to schedule their local/global updates. Particularly, at each time period $t$, we need to make the following participant selection and learning scheduling decisions for each model $m_j$. We denote $x_{i,j}^t$ or $y_{i,j}^t$ as the decision whether to select edge server $v_i$ as a parameter server or an FL worker for the $j$-th FL model $m_j$ at time $t$, respectively. Again, we assume that only one PS and $\kappa_j$ workers are selected for each model, i.e., $\sum\nolimits_{i=1}^{M}x_{i,j}^t = 1$ and $\sum\nolimits_{i=1}^{M}y_{i,j}^t = \kappa_j$. We use $\varrho_j^t \in [0, 1)$ to represent the maximal local convergence rate of $m_j$ at time $t$. We will use $\varrho_j^t$ and $\varsigma_j$ to control the number of global iterations and local updates for $m_j$ at time $t$. Recall that $\varsigma_j$ is given by $m_j$ as a requirement, thus only $\varrho_j^t$ is used for optimization. Overall, $x_{i,j}^t$, $y_{i,j}^t$, and $\varrho_j^t$ are the decision variables of our optimization in each time period $t$.

We now formulate our participant selection problem in multi-model FL where we need to select the parameter server and workers for each model and achieve the desired local convergence rate. The objective of our problem is to minimize the total cost of all FL models at time $t$ under specific constraints.

Here, $\varpi_{j}^{t}$ is the total FL cost of the $j$-th FL model in the $t$-th time period, which will be defined in Subsection 4.2. Constraints (4) to (7) make sure that the storage and CPU satisfy the FL model requirements. Constraint (8) ensures that the edge server stores the dataset that matches the FL model. Constraint (9) guarantees the number of the parameter server and FL workers of each model is 1 and $\kappa_j$, respectively. Constraint (10) ensures that each edge server only trains one FL model and can only play one role at a time. The decision variables and their ranges are given in (11). With nonlinear learning cost, this formulated optimization is a mixed-integer nonlinear program (MINLP) problem challenging to solve directly.

4.2   Cost Models

Our cost models consider four types of cost: edge communication cost, local update cost, global aggregation cost, and PS initialization cost, as defined in the followings, respectively.

Edge Communication Cost. The edge communication cost mainly consists of the FL model downloading and uploading costs. We denote by $\mu_j$ the uploaded and downloaded model size for the $j$-th FL model $m_j$. When uploading the FL model to the parameter server or downloading the FL model from the parameter server, we use the shortest path in the edge cloud to calculate the communication cost. Let $\rho_j(v_{i}, v_k)$ be the communication cost of model $m_j$ from edge server $v_{i}$ to $v_k$ at time $t$, and it can be calculated by

where $P_{i,k}^t$ is the shortest path connecting $v_i$ to $v_k$ at time $t$.

For $m_j$, the total edge communication cost is

Here, $v_i$ and $v_j$ are a worker and the PS of $m_j$, respectively.

Local Update Cost. Let $\psi(\cdotp)$ be the function to define CPU cycles to process the sample data $D_{j,i}^t$ used by the $j$-th FL model and stored in edge server $v_i$. Therefore all the local update cost for the $j$-th FL model in the t-th time period is defined as

Global Aggregation Cost. Similarly, we use $\psi(\cdotp)$ function to define CPU cycles to process the aggregation step for the uploaded FL model.

Initialization of Parameter Server. The parameter server needs to download the FL model assigned to it at time $t$ unless it has been the parameter server of the same FL model in the last time period. Let $v^t_{ps}(m_j)$ be the PS selected for model $m_j$ at time $t$. Then the initialization or switching cost of the parameter can be calculated as,

If the FL model is the first time to be trained or has not been updated at the last time period, the selected parameter server has to download model $m_j$ with cost $\eta_j$. If the parameter server stays the same from the last time period, there is no cost. Otherwise, the new parameter server needs to either download the model or transfer the model from the previous server.

Now, the total cost of the $j$-th FL model in time $t$ is given by

5.   Our Proposed Methods

In this section, we propose several multi-stage algorithms to attack the challenging optimization problem.

5.1   Three-Stage Method

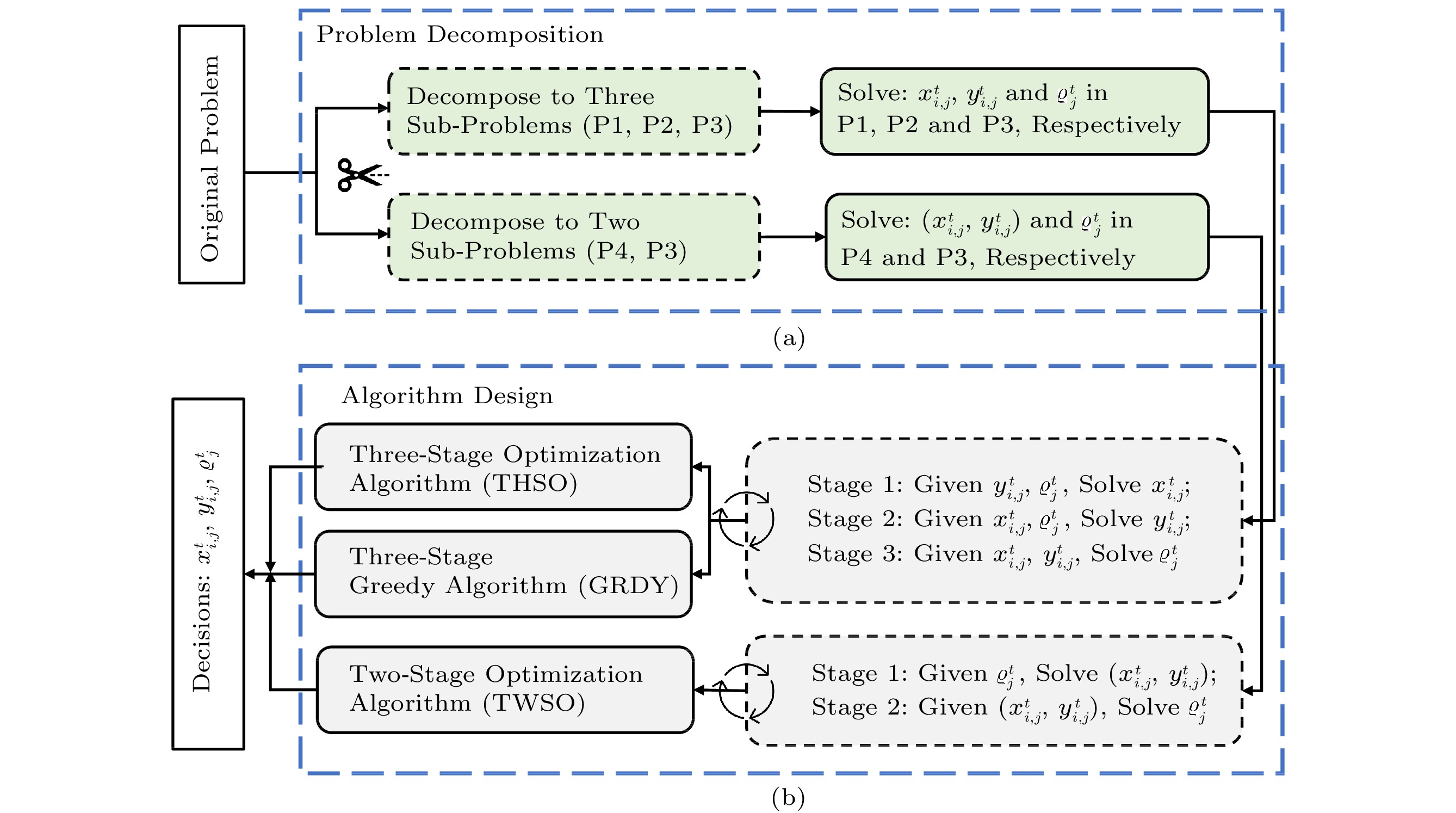
Recall that the formulated problem in Subsection 4.1 is a mixed-integer nonlinear program (MINLP), which is challenging to solve directly. Now, we decompose our original problem into three sub-problems and attack it via multiple iterations of solving the decomposed sub-problems, as shown in Fig.3.

Figure  3.  Problem decomposition and design of our proposed multi-stage algorithms. (a) The original problem is decomposed into either two or three subproblems. (b) Three different algorithms (two three-stage ones and a two-stage one) are then proposed to solve these sub-problems iteratively^[15].

下载: 全尺寸图片 幻灯片

5.1.1   Three-Stage Decomposition

The main idea is based on a three-stage decomposition. In each stage, we focus on solving only one of the decision variables of $x_{i,j}^t$, $y_{i,j}^t$, and $\varrho_j^t$ when the other two are fixed. We iteratively repeat these three stages until a certain specific condition is satisfied.

Stage 1: Parameter Server Selection. Given a worker selection and a local convergence rate, we aim to find a parameter server for each model to minimize the total cost, i.e.,

Stage 2: FL Worker Selection. We take the latest parameter server selection and fixed local convergence rate to select FL workers of each model to minimize the total cost, i.e.,

Stage 3: Local Convergence Rate Decision. With the latest PS and FL worker selections, we can determine the optimal local convergence rate in order to minimize the total cost, i.e.,

5.1.2   Three-Stage Algorithms

After we decompose the original problem into three sub-problems, we can solve each sub-problem by using either the linear programming technique or greedy heuristics. The basic idea shared by these methods is as follows. First, we randomly generate FL worker selection decision $y_{i,j}^{t,0}$ and the local convergence rate $\varrho_{j}^{t,0}$, and then solve the optimization problem P1 to get parameter server selection decision $x_{i,j}^{t,1}$. Second, given the local convergence rate $\varrho_{j}^{t,0}$ and the latest parameter server selection decision $x_{i,j}^{t, 1}$, we solve P2 to get FL worker selection decision $y_{i,j}^{t, 1}$. Last, based on the latest $x_{i,j}^{t, 1}$ and $y_{i,j}^{t, 1}$, we solve P3 to achieve the desired local convergence rate $\varrho_{j}^{t,1}$. This process will be repeated until it satisfies a specific condition (either no further improvement of the objective value of the optimization or reaching the maximal iteration number).

Algorithm 1 in Fig.4(a) shows the three-stage optimization method using the linear programming technique. Here, we leverage an optimization solver (PuLP)^[29] to solve each sub-problem for its convenience.

Figure  4.  Proposed algorithms^[15]. (a) Three-stage optimization (THSO). (b) Three-stage greedy (GRDY). (c) Two-stage optimization (TWSO).

下载: 全尺寸图片 幻灯片

Algorithm 2 in Fig.4(b) shows a three-stage greedy algorithm where greedy heuristic methods are used to solve the three sub-problems. 1) For stage 1, given a fixed worker selection and local convergence rate, we select a parameter server for each model with minimal cost. 2) For stage 2, we calculate the total cost of each potential edge server for each FL model and then sort the edge server list in ascending order of the cost. We greedily select the top $\kappa_j$ edge servers as FL workers for each model. 3) In the last stage, we greedily decrease the local convergence rate in a specific threshold to get the minimal total cost until it reaches the global convergence rate. We repeat the above steps until the ending condition is met.

Note that during the first two stages of Algorithm 2, we need to select the PS or workers for all models in a certain order. Obviously, the processing order of each model may affect the final performance. By default, we simply process them in a first come first serve mode, i.e., we first find the solution for the model that arrives earlier. Due to the heterogeneity of edge servers in the real edge cloud, some edge servers may have more sufficient resources (storage and computing capacity) while the others do not. In such a resource-limited scenario, serving the more complex FL model first may reduce the total completion cost of FL of all models. Therefore, we also introduce a variation greedy method in which the FL models are sorted based on their model sizes and we process models based on a larger model first in both the first and second stages of Algorithm 2. In this variation, the more complex FL model will first have more chance to select more high-performance workers leading to a lower total cost. In our experiments (Section 6), we have evaluated the impact of these two different processing orders. In addition, other ordering methods can also be applied to our proposed algorithm (Algorithm 2), such as choosing the model that requests more resources first.

5.2   Two-Stage Method

We can also combine the first two stages since both are with integer variables. Then the optimization can be solved via a two-stage decomposition. Here, we separate the integer variables ($x_{i,j}^t, y_{i,j}^t$) and the continuous variable $\varrho_j^t$ into two sub-problems, as shown in Fig.3.

Stage 1: Parameter Server and Worker Selection. Given the last local convergence rate, we want to find an optimal decision for selecting the parameter server and workers, i.e.,

Stage 2: Local Convergence Rate Decision. This is the same with the third sub-problem P3 in three-stage methods.

Here, we use an optimization solver (GEKKO)^[30] to solve the sub-problem P4 since it is a non-linear problem with two integer variables. For P3, we still use the PuLP solver. The detail of the two-stage method is given by Algorithm 3 in Fig.4(c).

5.3   Time Complexity

We now analyze the time complexity of each of the proposed algorithms. Here, we assume that the time taken to solve P1, P2, P3, and P4 with $N$ servers and $W$ models is $T_1(N,W)$, $T_2(N,W)$, $T_3(N,W)$, and $T_4(N,W)$, respectively. Given a decision of $x_{i,j}^t$, $y_{i,j}^t$, and $\varrho_j^t$, we can calculate the total learning cost with $T_{\rm cost}(N,W)$. Let $\epsilon$ be the step length of reducing the convergence rate in the stage 3 of Algorithm 2. Then it is easy to prove the following theorem regarding the time complexity of all proposed algorithms.

Theorem 1. The time complexity of Algorithms 1-3 is bounded by $O((T_1+T_2+T_3) \times max\_itr)$, $O\left(\left(N+({1}/{\epsilon})\right) \times T_{\rm cost} \times W \times max\_itr\right)$, and $O((T_4+$ $T_3)\times max\_itr)$, respectively.

Note that in Algorithms 2, the time complexity of stage 1 and stage 2 is bounded by $O(N \times T_{\rm cost} \times W)$ and $O\left(({1}/{\epsilon}) \times T_{\rm cost} \times W\right)$, respectively.

6.   Performance Evaluation

In this section, we present our experimental setup and evaluate the performance of our proposed methods via simulations.

6.1   Environmental Setup

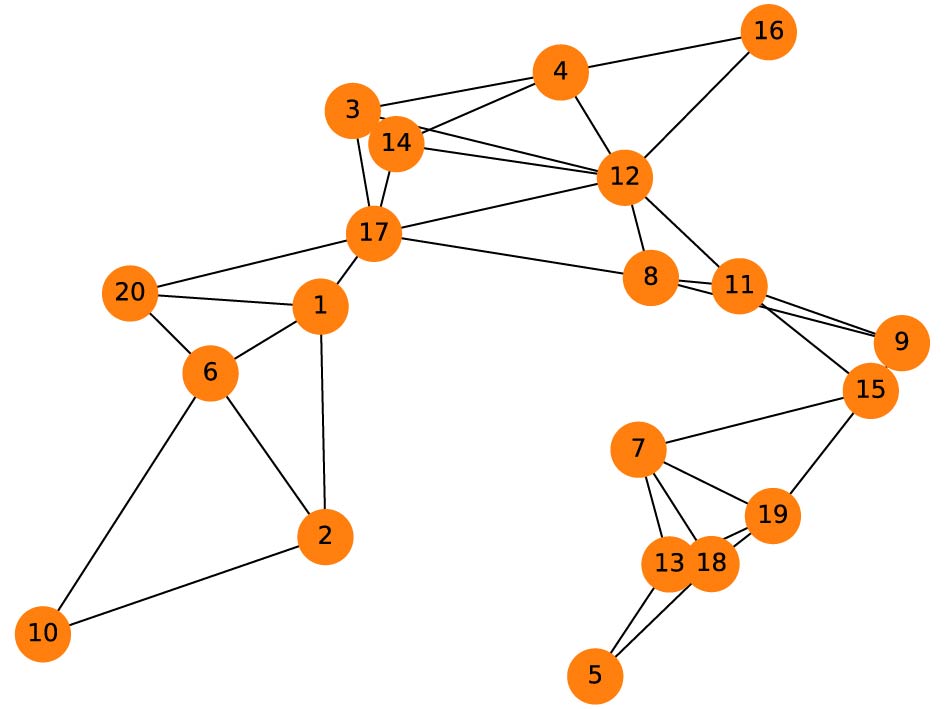
Edge Cloud. In our edge computing environment, we adopt different random topologies consisting of $20 - 40$ edge servers where the distribution of servers is based on the real-world EUA-Dataset^[31]. This dataset is widely used in edge computing and contains the geographical locations of 125 cellular base stations in the Melbourne central business district area. Fig.5 illustrates one example of topology used in our simulations. In each simulation, a certain number of edge servers are randomly selected from the dataset. Each edge server has a maximal storage capacity $c_i$, CPU frequency $f_i$, and link bandwidth $b_j$ in the range of 512 GB–1024 GB, 2 GHz–5 GHz, and 512 Mbps–1024 Mbps, respectively. We consider $O=5$ different data types (e.g., image, audio, and text) where the size $S_{i,k}$ is in the range of 1 GB–3 GB. Each type of data has been distributed in different edge servers and one edge server may store more than one type of data. Furthermore, the total number of time periods $T$ is set to 30.

Figure  5.  Example of edge cloud topology with 20 edge servers generated based on the real-world EUA-Dataset^[31].

下载: 全尺寸图片 幻灯片

Federated Learning Models. To verify the performance of the federated learning process, we conduct a set of federated learning experiments. We assume that there are $W$ different FL tasks (vision, audio, text, or data) running in our environment simultaneously. The number of FL workers $\kappa_j$ required by each model is in the range of 3–7. Each FL task has a specific model size $\mu_j$, CPU requirement $\chi_j$, and download cost $\eta_j$ in the range of 10 MB–100 MB, 1 GHz–3 GHz, and 1–5, respectively. The global convergence requirement and the two constant variables are set based on [9]: $\varsigma_j = 0.001$, $\vartheta_0 = 15$, and $\varphi_0 = 4$. Three classical datasets in scikit-learn 1.0.2^[32] are used to train linear regression (LR) models: the California Housing dataset, the Diabetes dataset, and randomly generated LR datasets. Each LR model is trained with the loss of Mean Square Error (MSE). In addition, we are interested in the performance of the proposed methods in non-convex loss functions. Hence, three different types of datasets are used for these FL tasks: Fashion-MNIST (FMNIST)^[33], Speech_Commands^[34], and AG_NEWS^[35]. Each of them is trained with a CNN model. We assign random data samples of these three datasets to clients in such a way that each client has a different amount of training and testing data. The Python library PyTorch (v1.10) is used to build the model. All experiments are tested on a Linux workstation including 16 CPU cores and 512 GB of RAM, and 4x NVIDIA Tesla V100 GPUs interconnected with NVlink2. Detailed parameters of both edge cloud and FL models are listed in Table 2.

Table  2.  Detailed Parameter Setting in Our Experiments

	Parameter	Value or Range
Edge cloud parameter	Number of edge servers $N$	$20 - 40$
	$v_i$'s storage capacity $c_i$ (GB)	$512 - 1\ 024$
	$v_i$'s CPU frequency $f_i$ (GHz)	$2 - 5$
	$e_i$'s link bandwidth $b_i$ (Mbps)	$512 - 1\ 024$
	Number of different datasets $O$	5
	Each dataset size $|S_{i,k}|$ (GB)	$1 - 3$
Federated learning parameter	Number of time periods $T$	30
	Number of FL models $W$	$1 - 5$
	Number of $m_j$'s FL workers $\kappa_j$	$1 - 7$
	$m_j$'s model size $\mu_j$ (MB)	$10 - 100$
	$m_j$'s CPU requirement $\chi_j$ (GHz)	$1 - 3$
	$m_j$'s downloading cost $\eta_j$	$1 - 5$
	$m_j$'s global convergence requirement $\varsigma_j$	$0.001 - 0.1$
	Constant FL variables $\vartheta_0$ and $\varphi_0$	15, 4

下载: 导出CSV 

| 显示表格

Baselines and Metrics. We compare our proposed algorithms (three-stage optimization THSO, three-stage greedy GRDY, and two-stage optimization TWSO) with four competitive methods ².

• ROUND^[9]. It selects the FL workers and the local convergence rate for each model based on a randomized rounding method^[9]. Since it does not consider the PS selection, we use a random choice for PS at the beginning.

• RAND. It randomly generates the parameter server selection, the FL worker selection decision, and the local convergence rate under certain constraints.

• DATA^[23]. It selects the FL workers based on the fraction of data at the servers and prefers the server with more data. Since it ignores the PS and local convergence rate selection, we randomly determine them.

• LOCAL^[24]. It selects its top workers that will complete the local training first (based on estimation). Again random decisions are used for the PS and local rate.

The main metrics used for evaluation are the average total FL learning cost and the average accuracy (or the average training loss and the average R2 score for LR) of FL models.

6.2   Evaluation Results

Via extensive simulations, we evaluate the performance of our methods mainly focusing on their cost performances.

6.2.1   Performance Comparison—Total Learning Cost

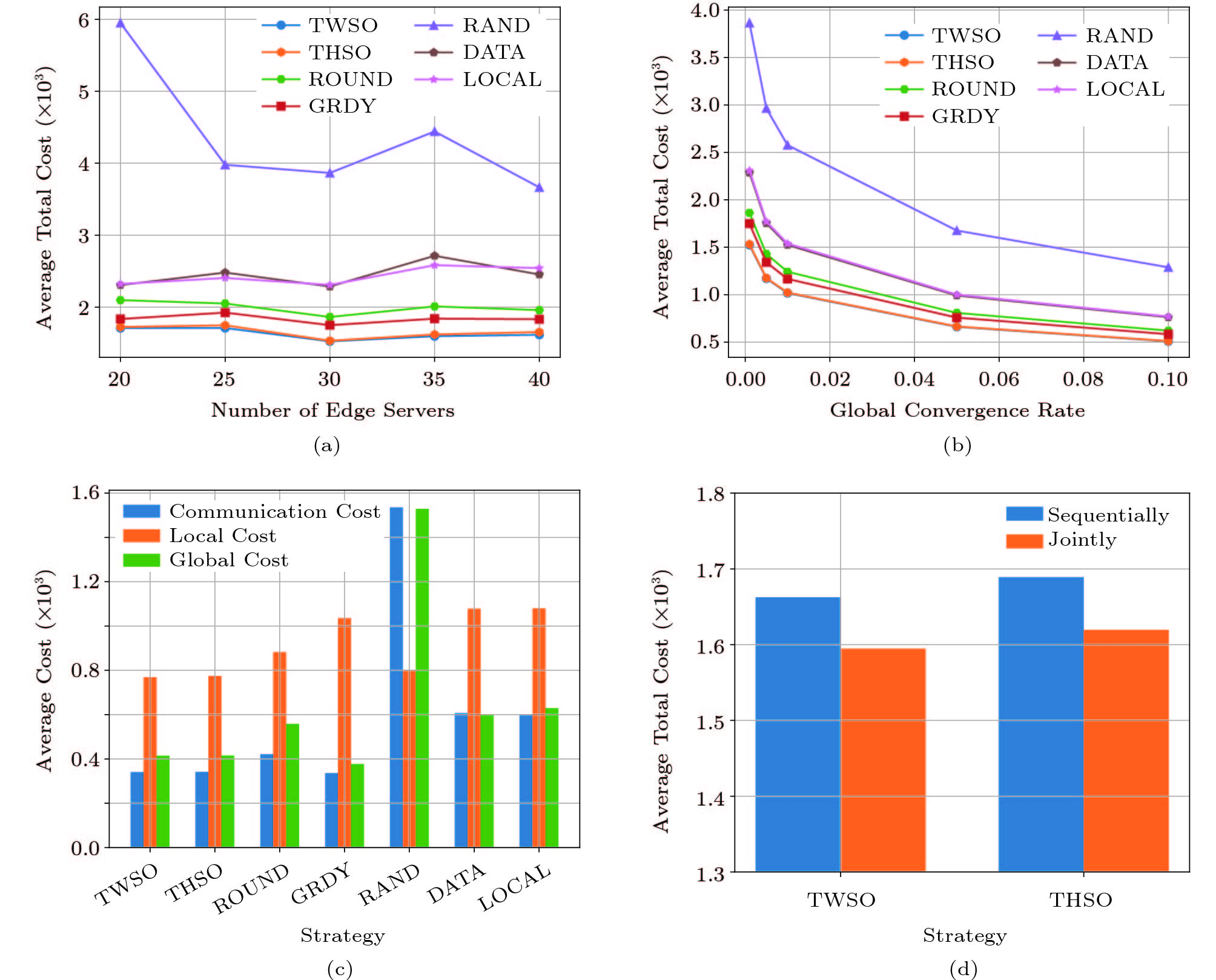
We first investigate different algorithms with a different number of edge servers and global convergence rates. We consider three FL models for three different types of tasks (i.e., image classification, speech recognition, and text classification) to be trained simultaneously, where each FL model has requested five FL workers. Figs.6(a) and 6(b) show the results of two groups of simulations. In the first group, we set the number of edge servers to be from 20 to 40, while fixing the global convergence rate at 0.001. In the second group, we change the global convergence rate from 0.001 to 1.1 with 30 edge servers. We have the following observations.

Figure  6.  Performance comparison with (a) different number of edge servers, (b) different global convergence rates, (c) detailed costs of different methods, and (d) single model vs multiple models^[15].

下载: 全尺寸图片 幻灯片

First, clearly for both sets of simulations, our proposed three algorithms (TWSO, THSO, and GRDY) have better performance than the other four benchmarks in terms of average total learning cost. Having better performances than ROUND (which focuses on worker selection and learning rate optimization) confirms the advance of our methods by considering the PS selection in the joint optimization. The better performances of our methods and ROUND compared with DATA and LOCAL (which only focus on the worker selection) show the advantage of joint optimization. In all simulations, RAND has the worst performance since it does not take any optimization.

Second, as shown in Fig.6(a), the average total cost of every algorithm decreases first and increases again as the number of edge servers increases. Initially, with more edge servers, all algorithms have better chances to find a good solution to minimize the total cost of all FL models. On the other hand, the further larger topology with more servers may also begin to increase the average total cost due to larger transmission costs from workers to PS.

Third, as shown in Fig.6(b), as the global convergence rate increases, the average total cost decreases. This is reasonable since the larger global convergence rate requests less local training or global update, which leads to lower total learning costs.

Fig.6(c) also plots the detailed costs of different methods when 30 edge servers are considered, and the global convergence rate is 0.001. It shows that the local cost dominates the total cost, and consequently, GRDY has a higher total cost than TWSO and THSO as seen in Fig.6(a).

We also evaluate the effects of joint optimization over multi-models compared with the separative optimization with only a single model. In the latter case, we still use TWSO and THSO but force them only on a single FL model at a time, and thus sequentially choose the decision for each model. Again we train three FL models when 30 edge servers are considered and the global convergence rate is 0.001. Fig.6(d) shows the comparison of determining the choices for three FL models jointly or sequentially with TWSO and THSO. We can clearly see the lower total cost when we jointly optimize the decisions. This confirms the effectiveness of jointly determining the selection decision for multiple FL models rather than sequentially determining the decision for every single model.

6.2.2   Impact of FL Model Number

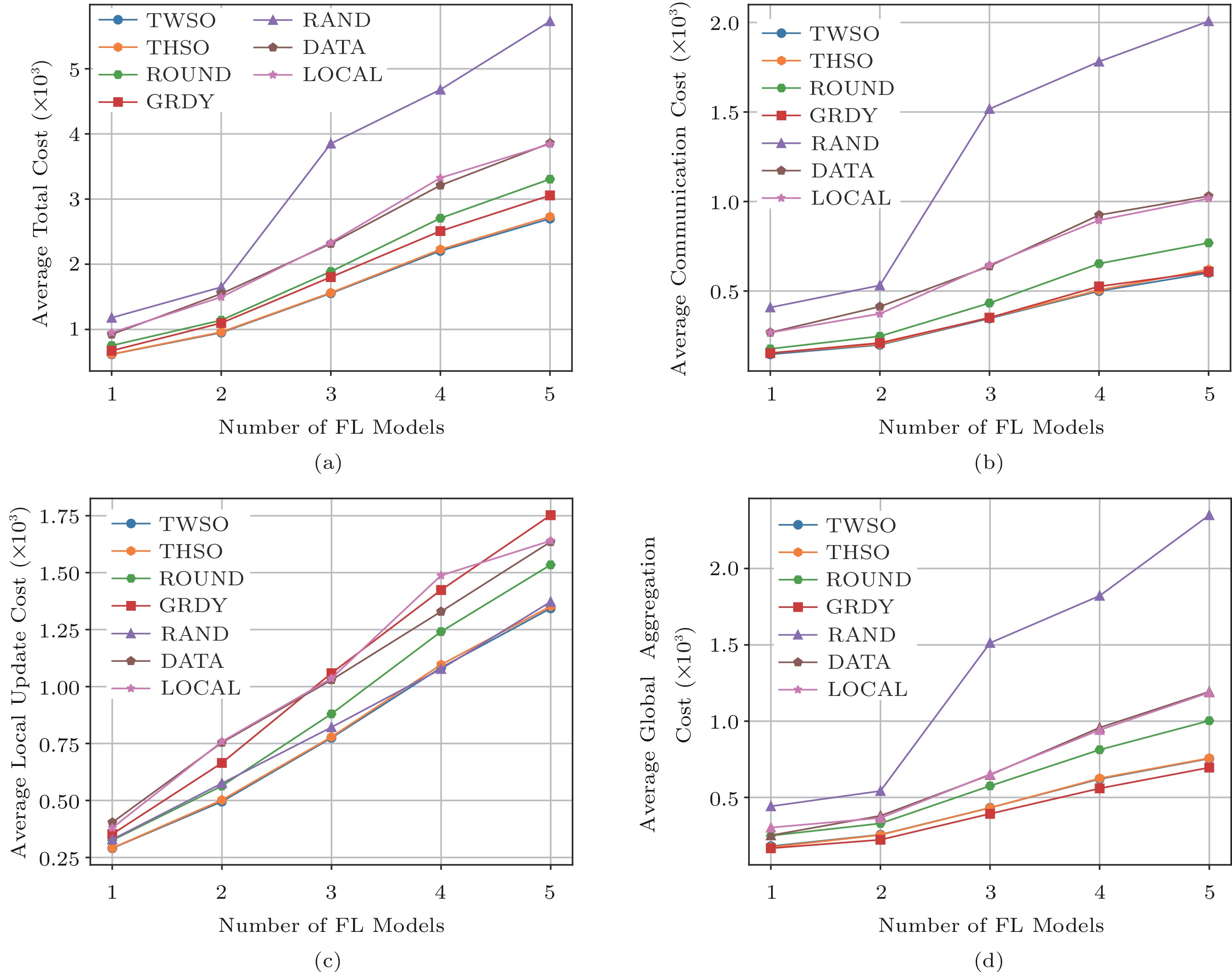
Next, we look into the impact of different numbers of FL models. We simultaneously run one to five FL models. The number of edge servers and the number of FL workers are set to 30 and 5, respectively. The global convergence rate is also set to 0.001. As shown in Fig.7(a), the more FL models, the more the average total learning cost. Our proposed algorithms still perform better than the other four methods. TWSO and THSO still enjoy a little performance improvement against GRDY. We also plot the detail of three types of costs (i.e., communication cost, local cost, and global cost) in Fig.7(b), Fig.7(c), and Fig.7(d) respectively. We can observe that the communication cost of GRDY is similar to those of TWSO and THSO. However, GRDY has the highest local cost and the lowest global cost compared with the other algorithms. That is because GRDY greedily runs more local training so that the number of global updates can be reduced while satisfying the expected global convergence rate.

Figure  7.  Impact of the number of FL models on costs^[15]. (a) Average total cost. (b) Average communication cost. (c) Average local update cost. (d) Average global aggregation cost.

下载: 全尺寸图片 幻灯片

6.2.3   Impact of FL Worker Number

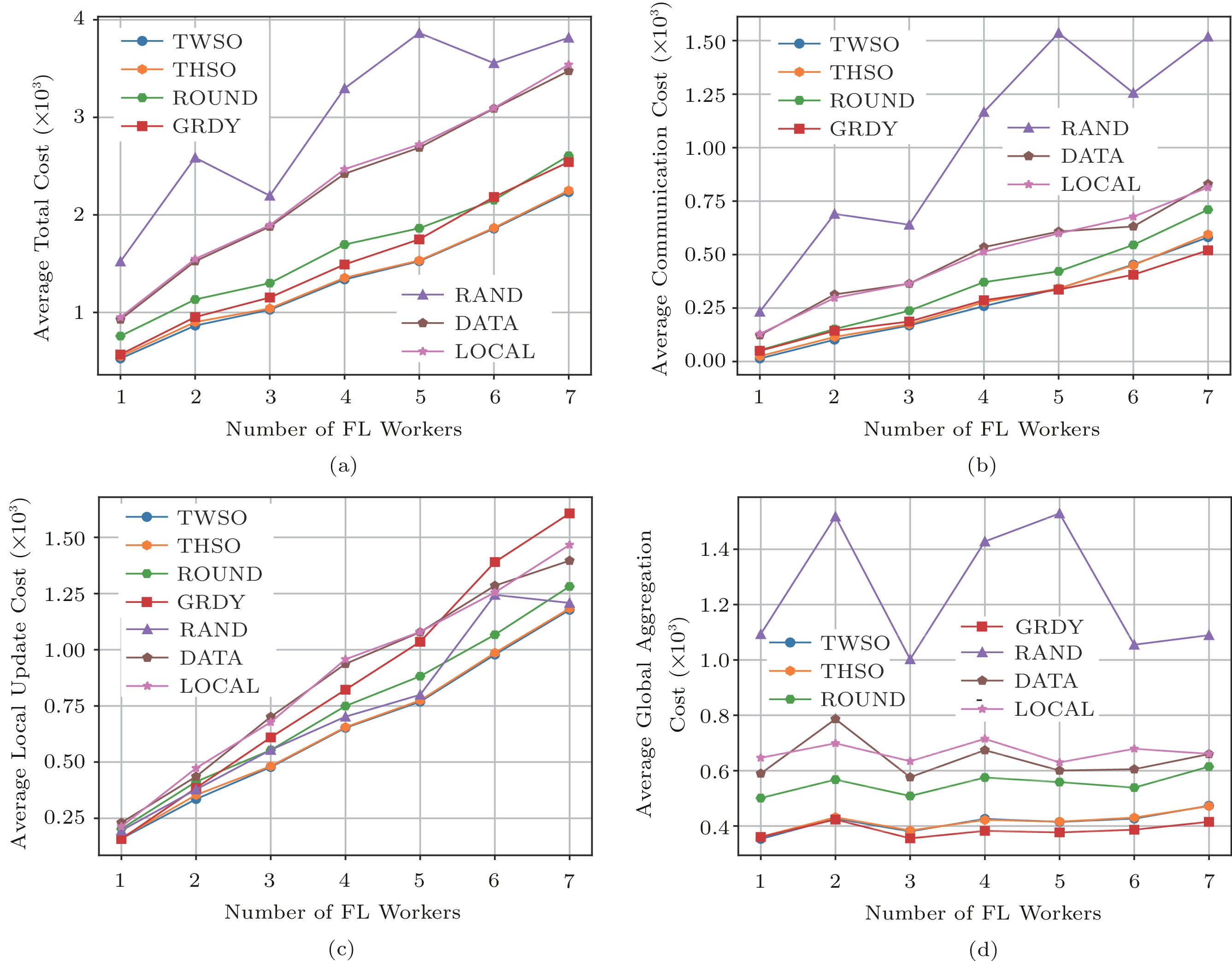
We further investigate the impact of a different number of FL workers. We consider 30 edge servers and train three FL models while the global convergence rate is 0.001 as well. Results are reported in Fig.8, which are similar to those with a different number of FL models. First, the average total cost of all algorithms increases as the number of FL workers increases since the more FL workers, the more resource-consuming. Second, the proposed algorithms have better performance than ROUND, RAND, DATA, and LOCAL as shown in Fig.8(a). Last, GRDY has the highest local cost while having the lower communication cost and global cost compared with other strategies as shown in Figs.8(b)–8(d).

Figure  8.  Impact of the number of FL workers on costs^[15]. (a) Average total cost. (b) Average communication cost. (c) Average local update cost. (d) Average global aggregation cost.

下载: 全尺寸图片 幻灯片

6.2.4   Impact of Model Processing Order in GRDY

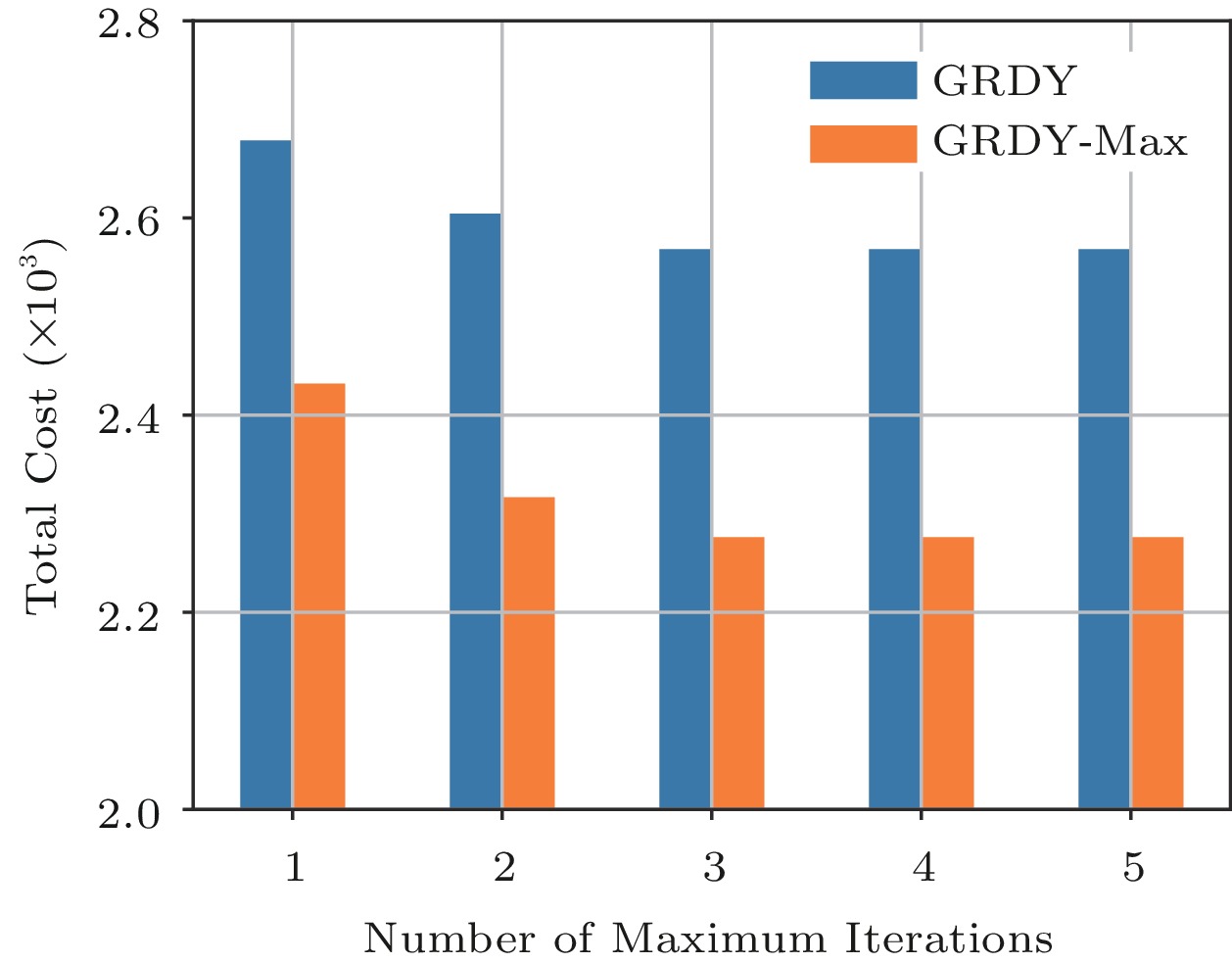
Remember that in GRDY (Algorithms 2) we need to select the PS and workers for each model following certain processing order among FL models. We now study the impact of different processing orders in GRDY. We test on two specific processing orders: the default one with First-in-First-Serve (GRDY) and the variation in which priority is given to the model with a larger size (GRDY-Max). The experiments run under the edge cloud with 30 edge servers that have limited resources and significant differences. We run 20 different cases in each different number of maximum iterations, and Fig.9 shows the experimental result. First, as the number of maximum iterations increases, the total cost of both two greedy algorithms decreases since they have more chances to find a better solution with a lower cost. However, the improvement becomes smaller when the maximum iteration further increases. Second, under the resource-limited scenario, GRDY-Max performs better than GRDY in almost all cases. This result confirms the necessity and superiority of selecting an optimal processing order in different edge scenarios. In addition, we need to select an appropriate maximum iteration to control the convergence speed of our greedy algorithms.

Figure  9.  Total cost comparison of two different processing orders of FL models in GRDY and its variation GRDY-Max.

下载: 全尺寸图片 幻灯片

6.2.5   FL Training Loss and Accuracy

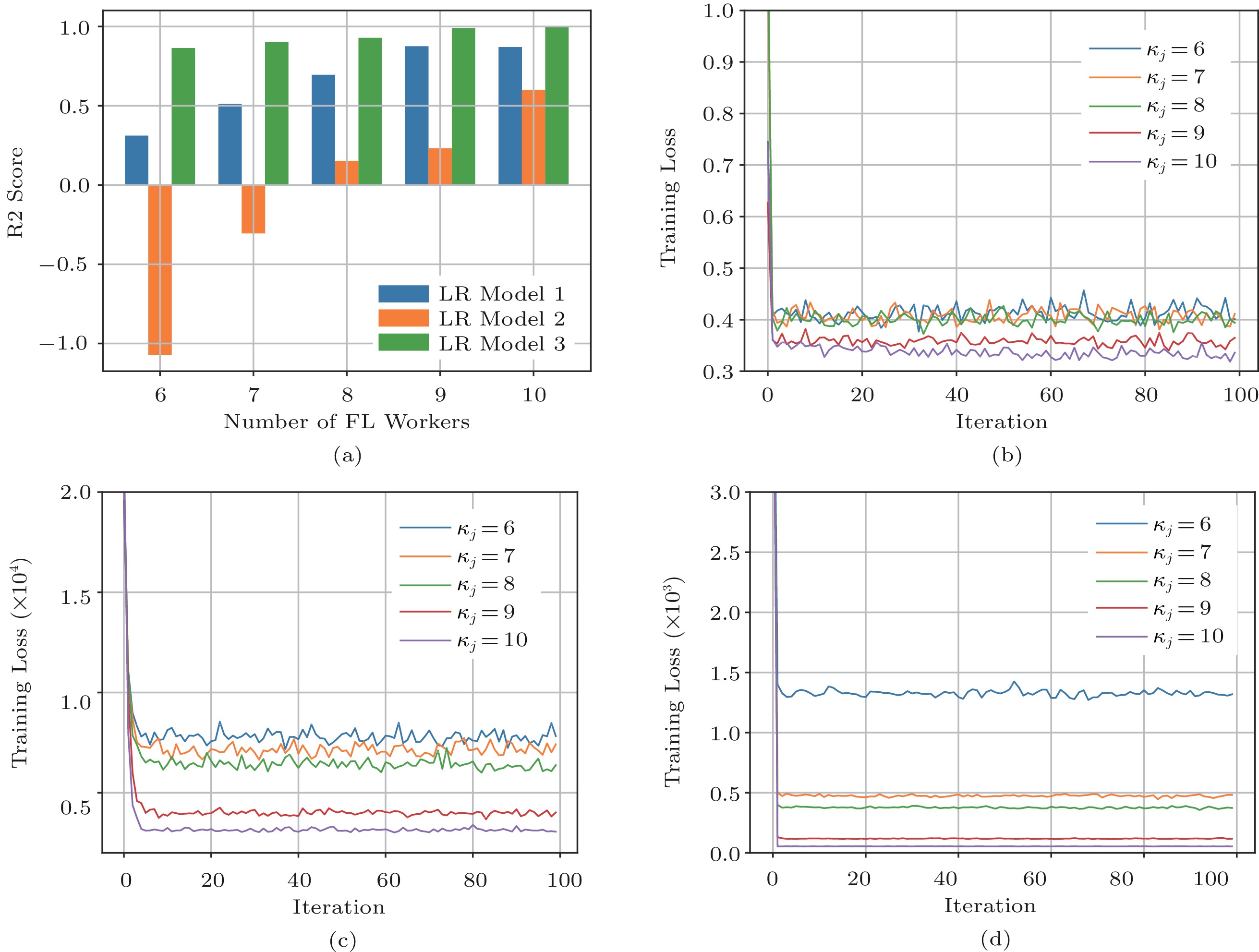
Fig.10 shows the training loss of our method in real-world federated learning experiments over LR datasets. We introduce the R2 score metric to evaluate the performance of LR (Linear Regression) model (convex) training. The R2 score is the proportion of the variance in the dependent variable that is predictable from the independent variable(s). In this set of experiments, we concurrently train three LR models with three different datasets. Each dataset is split into 10 edge servers unequally (i.e., non-IID setting), and the number of global training rounds is 100. We can see from Figs.10(b)–10(d), the training loss decreases as the number of workers ($\kappa_j$) increases for each model. Fig.10(a) shows the R2 score of all LR models. Obviously, with more workers, the R2 scores of all models increase, which means all models are well-regressed. However, model 2 has a worse R2 score (a negative value) in fewer workers due to the small size of the training dataset. But as the number of workers increases, the performance of model 2 becomes better.

Figure  10.  Training loss with LR models/tasks and the impact of the number of FL workers. (a) R2 score of three LR models. (b) Training loss of Linear Regression over the California Housing dataset. (c) Training loss of Linear Regression over the diabetes dataset. (d) Training loss of Linear Regression over a randomly generated dataset.

下载: 全尺寸图片 幻灯片

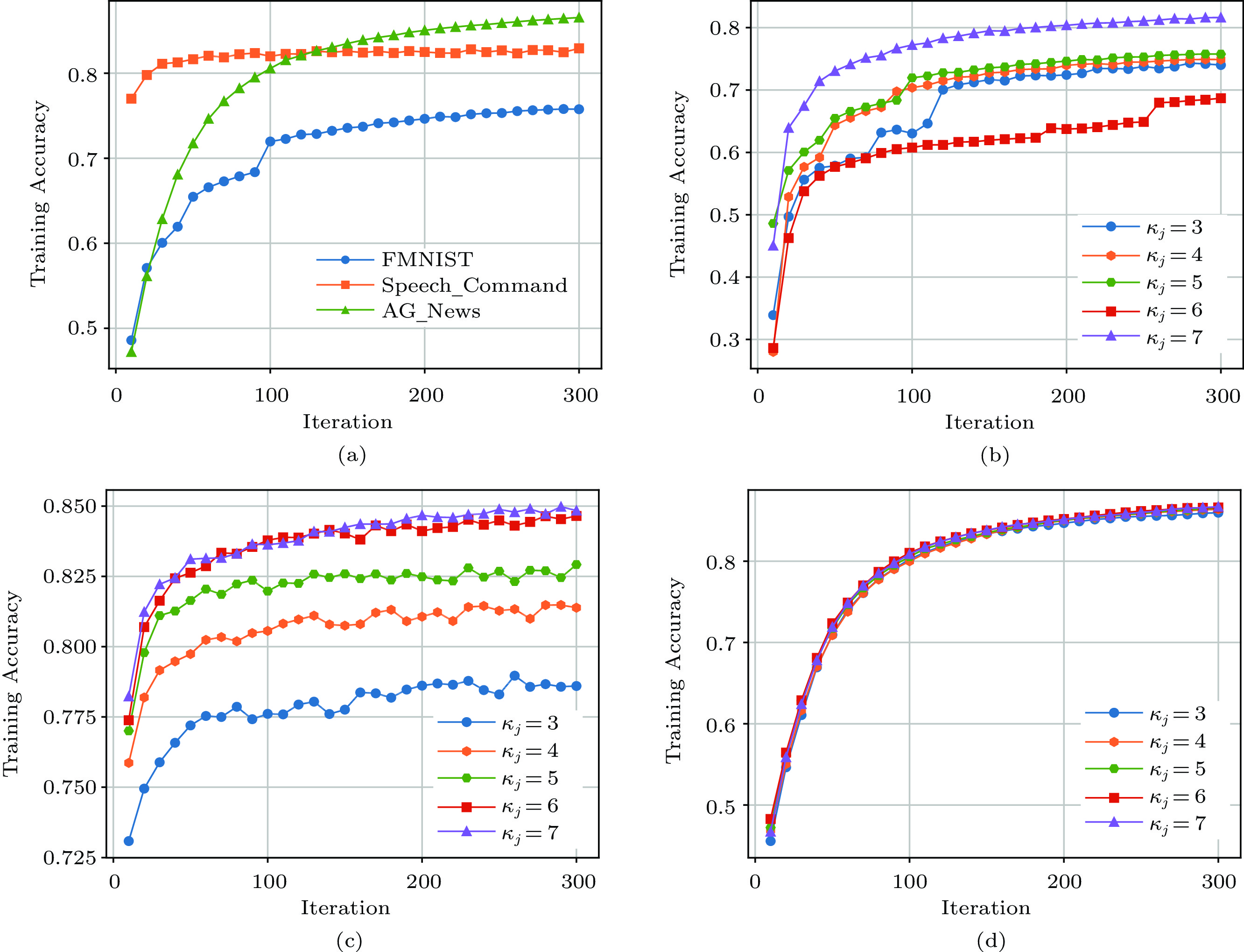
Fig.11 also reports the learning accuracy of our method on more complex FL tasks with different numbers of workers (due to space limitation, we only show the one from THSO). Here, the datasets of three FL models (image classification, speech recognition, and text classification) are split into 30 partitions and the number of the global update is set to 300. Fig.11(a) shows the training accuracy of all three FL models increases with the increasing number of iterations. Figs.11(b)–11(d) show the detailed training accuracy of three different models with different numbers of FL workers. We can observe that with more FL workers, the training accuracy of all models can reach a higher value. However, when comparing the result in Fig.8, the more FL workers, the more total cost consumed. Hence, there is a trade-off between the training accuracy and the total cost. Another interesting observation is that for FMNIST and Speech_Command, the accuracy increases with more FL workers, but for AG_News, the accuracy is similar or the difference is very minimal. This may be due to the simplicity of the AG_News learning task. In summary, one needs to consider the trade-off between the training accuracy and the total cost. If you need more FL workers, it will incur more total cost but get higher training accuracy, and vice versa.

Figure  11.  Training accuracy with three FL tasks and the impact of FL workers^[15]. (a) Accuracy of three FL models with 30 edge servers and 5 workers. (b) Accuracy of image classification over FMNIST. (c) Accuracy of voice recognition in Speech_Command. (d) Accuracy of text generation in AG_News.

下载: 全尺寸图片 幻灯片

7.   Conclusions

In this paper, we mainly focused on multi-model FL over an edge cloud and carefully selected participants (both PS and workers) for each model by considering the resource limitation and heterogeneity of edge servers as well as different data distributions. We formulated a joint participant selection and learning optimization problem to minimize the total FL cost of multiple models while ensuring their convergence performance. We proposed three different algorithms to decompose the original problem into multi-stages so that each stage can be solved by an optimization solver or a greedy algorithm. Extensive simulations with real FL experiments showed that our proposed algorithms outperform similar existing solutions. In the future, we plan to further investigate: 1) reinforcement learning based solutions for similar optimization problems in a more dynamic edge system, 2) the extension of proposed multi-stage methods over multiple time-scales, where learning schedule and participant selection can be optimized at fast and slow timescales separately, similar to [22], 3) new quantum-assisted methods for similar optimization problems^[36], 4) new joint optimization problems where different FL models can choose different FL structures (such as DFL^[10] or HFL^{[5, 8, 11]}), and 5) similar joint optimization problems but in a more complex edge system with multiple edge operators.